Также опубликовано в отдельном блоге автора.
AB-тесты сейчас применяет, возможно, каждый второй менеджер продукта, однако далеко не всегда ясно, как же интерпретировать результат теста и какой уровень статистической значимости использовать. Используем слишком высокий - тесты возможных улучшений будут проваливаться, хотя улучшения на самом деле есть. Используем слишком низкий - часто будем получать "подтверждения" ложных улучшений.
Независимо от выбранного уровня значимости, принимая решения по результатам AB-тестов, время от времени мы будем ошибаться и наносить ущерб бизнесу. Выбирая уровень статистической значимости тестов (или что то же самое - граничные p-value), мы можем ограничить количество ошибок и балансировать между пользой от оправданно успешных экспериментов и ущербом от ошибочно успешных.
Регистрация по номеру телефона
Представьте себе, что вы - менеджер продукта в корпорации, занимающейся веб-сервисами.
Вы работаете над повышением количества регистраций, внимательно рассматриваете этапы прихода новых пользователей, замечаете, что многие отваливаются на этапе ввода своего email и решаете попробовать заменить email на номер телефона. Пусть это не совсем общепринято и требует отправки небесплатной смски, но сегодняшние пользователи не очень любят электронную почту и часто регистрируются прямо с телефона.

Что же, это - вполне традиционная задача менеджера продукта. Мы - современная компания и до принятия больших решений, тем более требующих небесплатных смсок, стараемся проверять: улучшают ли ситуацию наши идеи на самом деле. Соответственно конструируем два варианта регистрации: старый - с email'ом и новый - с номером телефона. Показываем каждый вариант случайно выбранным пяти процентам анонимных посетителей сайта, затем измеряем какая доля посетителей успешно ввела email/телефон и активировала эккаунт в течение, скажем, суток с момента регистрации.

Планирование эксперимента
Допустим, мы спланировали эксперимент с любым из обычных калькуляторов оценки требуемого количества пользователей, всё сделали аккуратно, выбрали одностороннюю гипотезу (нас интересуют только улучшения) и.. какой же уровень статистической значимости выбрать?
Довольно часто в компаниях есть "обычный" уровень значимости, который выбирают просто потому, что так принято, - допустим, 95%. Однако не подойдёт ли в данном случае уровень значимости 90% или даже 80%? Ведь не хотелось бы отказаться от полезного улучшения, только потому что мы, мол, не абсолютно уверены в улучшении - на все сто ведь никогда нельзя быть уверенным.
Что результаты значат на самом деле
Допустим, мы выбрали 90%-тную значимость, опасаясь, что при большей тест может провалиться, а меньшую вроде бы никто вокруг нас не применяет. Запустили тест, он работал ровно пять полных недель (полных - чтобы сгладить возможное отличие поведения пользователей в будни и на выходных), каждый вариант увидело примерно 10000 человек, тест завершился успешно, калькулятор сообщил что-то вроде "p-value is 0.07, You can be 90% confident that this result is a consequence of the changes you made". Что же на самом деле это означает?
Один из простых способов интерпретировать AB-тест - идти от обратного. На самом деле мы ведь никогда не можем быть полностью уверенными, что предложение вводить телефонный номер в среднем приносит больше регистраций. Всегда есть вероятность, что на длительном периоде времени телефонные регистрации приносят столько же пользователей, сколько email-регистрации или даже меньше, но вот именно на тех неделях, когда мы проводили тест, случайная флуктуация принесла больше телефонных регистраций, чем емейл-регистраций.
Если телефонные регистрации ничуть не лучше, в некоторых тестах они всё равно будут случайно выигрывать.
P-value AB-теста как раз и показывает, насколько редкое событие мы наблюдаем, если бы предложение вводить номер телефона на самом деле (на длительном периоде времени) ничего не улучшало, а возможно даже и ухудшало.
Представьте себе, что в такой печальной ситуации мы провели бы не один, а сотню одинаковых AB-тестов: каждый по те же пять недель, каждый по 10000 посетителей на вариант. В большинстве таких ста тестов телефонный вариант принесёт меньше регистраций, чем email-вариант или столько же, как и email-вариант. Однако в части тестов телефонный вариант может принести немного больше регистраций.
Наблюдаемое p-value 0.07 как раз и означает, что если телефонный вариант на самом деле ничуть не лучше email'ового, то оказаться впереди email'ового столь сильно или ещё сильнее, чем мы наблюдаем, он смог бы в семи тестах из ста.

Выбор уровня статистической значимости показывает, насколько редкой должна быть наблюдаемая разница в конверсиях между телефонным и email'овым вариантами, чтобы мы всё же признали такую разницу слабо объяснимой случайной флуктуацией и решили переключиться на телефонные номера.
Стоимость ошибочного выигрыша
Ключевой момент интерпретации состоит в том, что даже если мы всё проводим аккуратно, без технических и логических ошибок, то наши AB-тесты всё равно время от времени обязательно будут "подтверждать" ложные гипотезы. Если мы будем принимать решения на основании тестов, то периодически будем ошибаться. Мы лишь можем ограничить количество ошибок, выбирая тот или иной уровень статистической значимости.
Если ошибиться очень опасно (без регистрации пользователей мы ничего не продадим!) - выбираем высокий уровень значимости. Однако высокий уровень значимости не придёт бесплатно: придётся очень значительно увеличивать длительность тестов, либо уверенно выигрывать смогут лишь варианты, дающие очень значительный прирост. В результате будем либо упускать небольшие возможности улучшения, либо будем успевать проводить очень мало экспериментов.
В общем-то пользу от теста и стоимость возможных ошибок при том или ином уровне значимости можно прикинуть с помощью очень простых расчётов. В примере ниже мы подсчитываем результат в новых пользователях, но не намного более сложным образом можно оценивать ожидаемые результаты и в деньгах.
Пользуясь нашими знаниями предметной области и историей предыдущих улучшений предположим, что удачный переход на телефонные регистрации повысит конверсию процентов на 5, а если мы ошибочно перейдём на телефонные регистрации, то возможно и половина посетителей не сможет или не захочет регистрироваться (откуда именно берём такие допущения расскажем ниже).
Среднее количество регистраций в неделю | 2000 |
Насколько больше пользователей может приносить телефонная регистрация по сравнению с емейловой | 5% |
Насколько меньше пользователей может приносить телефонная-регистрация в случае ошибки | 50% |
Если всё отлично, то год работы с смс-регистрацией принесёт дополнительно пользователей | 52 * 2000 * 5% = 5200 |
Если ошибочно внедрили смс-регистрации, то за год недосчитаемся пользователей | 52 * 2000 * 50% = 52000 |
Выбранный граничный уровень значимоcти | 95% |
Если бы не проводили никаких улучшений, то за год появилось бы пользователей | 52 * 2000 = 104000 |
Если бы проводили подобные эксперименты постоянно и принимали решения с таким же уровнем значимости, то за год средний эксперимент мог бы принести дополнительно пользователей | 95% * 5200 - (100%-95%) * 52000 = 2340 |
Пользы от среднего подобного эксперимента в процентах роста аудитории | = 2340 / 104000 = 2.25% |
Эту табличку можно найти в Google Sheets и скопировать себе.
Выбор уровня статистической значимости
Откуда же до начала эксперимента подставлять в такую таблицу ожидаемую пользу от справедливо выигравшего теста (5% в нашем примере) и возможный вред в случае ошибки (50% в нашем примере)? Лучше всего, конечно, опираться на историю подобных изменений. Если это далеко не первый эксперимент с улучшением воронки регистраций, и большинство из предыдущих увеличивало конверсию на пару процентов, то вряд ли даже очень значительная идея улучшит сильнее, чем на 5-10%.
Если истории подобных внедрений нет или она незначительна, то я не знаю метода лучше, чем экспертные оценки и страхи. Всё же вряд ли аж половина потенциальных пользователей не регистрируется, потому что не хотят / не могут вводить email, а телефон с радостью ввели бы. В лучшем случае миграция на номер телефона подтянет долю регистрирующихся с 7.7% может быть до 8% (улучшение на 5%). А вот если мы ошибаемся и пользователи на самом деле вообще не хотят доверять нам номер телефона, то можно/страшно потерять и половину регистраций.
Числа в таблице подобраны таким образом, что при 90%-тной значимости эксперимент не имеет смысла - мы слишком часто будем ошибаться проводя подобные эксперименты раз за разом. При 95%-тной значимости же, кажется, что средний подобный эксперимент может принести пользу, но не очень большую - всего-то пару процентов дополнительных пользователей за год после внедрения улучшения. Стоит ли в таком случае вообще проверять идею телефонных регистраций экспериментом или лучше принять решение основываясь на интуиции начальства, или просто сделать так, как поступают наши конкуренты?
Не уверены - проверяем строже
Что же, если вся предыдущая команда сервиса была уволена вчера, мы очень мало знаем, о рынке и потенциальных пользователях, то действительно, наши идеи могут иметь мало смысла и неплохо бы проверять идеи улучшений построже.
Например, давайте подставим в таблицу невероятно высокие страхи: 99% потери регистраций в случае ошибки (в нашей стране неожиданно входящие СМС оказались платными, и вообще никто не хочет регистрироваться по смс), а возможный положительный эффект оцениваем всего лишь в 2-3%. Даже в столь печальной ситуации, когда мы не уверены ни в рынке, ни в своих идеях, стоит нам выкрутить статистическую значимость на 99% - и волна подобных экспериментов всё же принесёт заметную пользу. Эксперименты станут занимать невероятно много времени, но если в воображаемом мире оно у нас есть - неработающие идеи будут внедряться крайне редко.
Небольшое улучшение, повторённое много раз, - большое улучшение
Дополнительные пара процента пользователей в год - не очень много, если только у вас уже не миллионы пользователей. Однако два десятка подобных скромных экспериментов проведённых один за другим уже принесут почти 50% дополнительных пользователей (20 повторений 2.25% улучшения из нашего примера принесут 56%: 1.0225^20 ≈ 1.56 ).
Культура постоянных небольших экспериментов к сожалению может отвлекать от придумывания действительно прорывных идей, но может принести очень немаленькую пользу, оптимизируя существующие решения.
Можно наблюдать и после принятия решений
Было бы здорово даже в случае выигравшего эксперимента понаблюдать за пользователями более долговременно. Например, если по результатам наших пяти недель регистрация по номеру телефона выиграла, мы можем включить её для 95% анонимных посетителей. Оставшимся пяти процентам можно предлагать по прежнему email и сравнить результаты различных вариантов не через пять, а через 25 недель.
Если применять подобный подход пост-внедренческих тестов постоянно, то можно учесть его и в прикидочной таблице - вполне можно ограничить негативный эффект ошибочного внедрения, например, четырьмя месяцами, если эти четыре месяца после внедрения проверять, нет ли не всё же негативного эффекта от внедрения. Это позволит проводить эксперименты с ещё более низким уровнем значимости (а значит - мы сможем проводить их чаще) ценой головной боли с наличием ещё большего количества вариантов сайта, работающих одновременно, и сложности с публичными анонсами внедрений (у некоторых пользователей старое решение может показываться ещё четыре месяца).
Проверяйте идеи, имеющие смысл
К счастью или к сожалению, но статистические исследования не избавляют от необходимости думать. Понимание рынка и его стандартов, пользователей и истории сервиса позволяет формулировать гипотезы, имеющие больший шанс улучшить ситуацию.
Если вы занимаетесь сервисом не первый год и знаете, что им пользуются для заказа рабочих инструментов, то вряд ли даже очень неудобная регистрация оттолкнёт больше нескольких процентов пользователей - инструменты ведь заказывать таки надо. Соответственно в прикидочной таблице страх потери можно ограничить, скажем, в 20% и внезапно окажется, что нам достаточно уровня значимости в 85% или даже в 80%, что радикально сократит затраты времени требуемого для эксперимента.
Если вы знаете, что по результатам прошлых лет даже самые радикальные изменения не улучшают/ухудшают ситуацию больше, чем на несколько процентов (например, новые пользователи приходят в основном по сильной социальной рекомендации), то и в оценочную таблицу можно вписывать подобные цифры. Например, возможную пользу оценим в 2%, а возможный вред - в 5%. В результате снова окажется, что достаточно и 80% уровня значимости и эксперимент можно провести очень быстро.
Если вы опасаетесь, что вот именно данная идея несёт в себе очень большой риск (действительно почти все потенциальные пользователи откажутся давать свой номер телефона), то может быть стоит придумать менее рискованный эксперимент, позволяющий проверить гипотезу о желаниях пользователей способом менее разрушительным в случае ошибки? Например, почему бы не попробовать принимать и телефон, и емейл - это резко уменьшит потенциальный негативный эффект (уйдут только те, кто не разберётся, чего же от них хотят), а окончательно отказаться или не отказаться от email можно будет по результатам долговременного анализа - просто посмотрев на то, что пользователи предпочитают использовать.

Некоторые изменения имеет смысл проводить, даже если мы не можем подтвердить положительный эффект
Если стратегия компании - перевод всех-всех-всех сервисов на идентификацию клиентов по номеру телефона или, что чаще встречается, - перевод на новые корпоративные цвета и стили, то нужно иметь очень серьёзные аргументы, чтобы отказаться от внедрения. Если калькулятор длины эксперимента показывает безумные числа необходимой длительности для надёжного опровержения отрицательного или нулевого эффекта изменений, попробуйте спланировать эксперимент, подтверждающий, что изменение, если даже и ухудшает ситуацию, то не более чем на пару процентов. Например, вот этот калькулятор позволяет такое.
Как же подходить к выбору уровня значимости и анализу результатов?
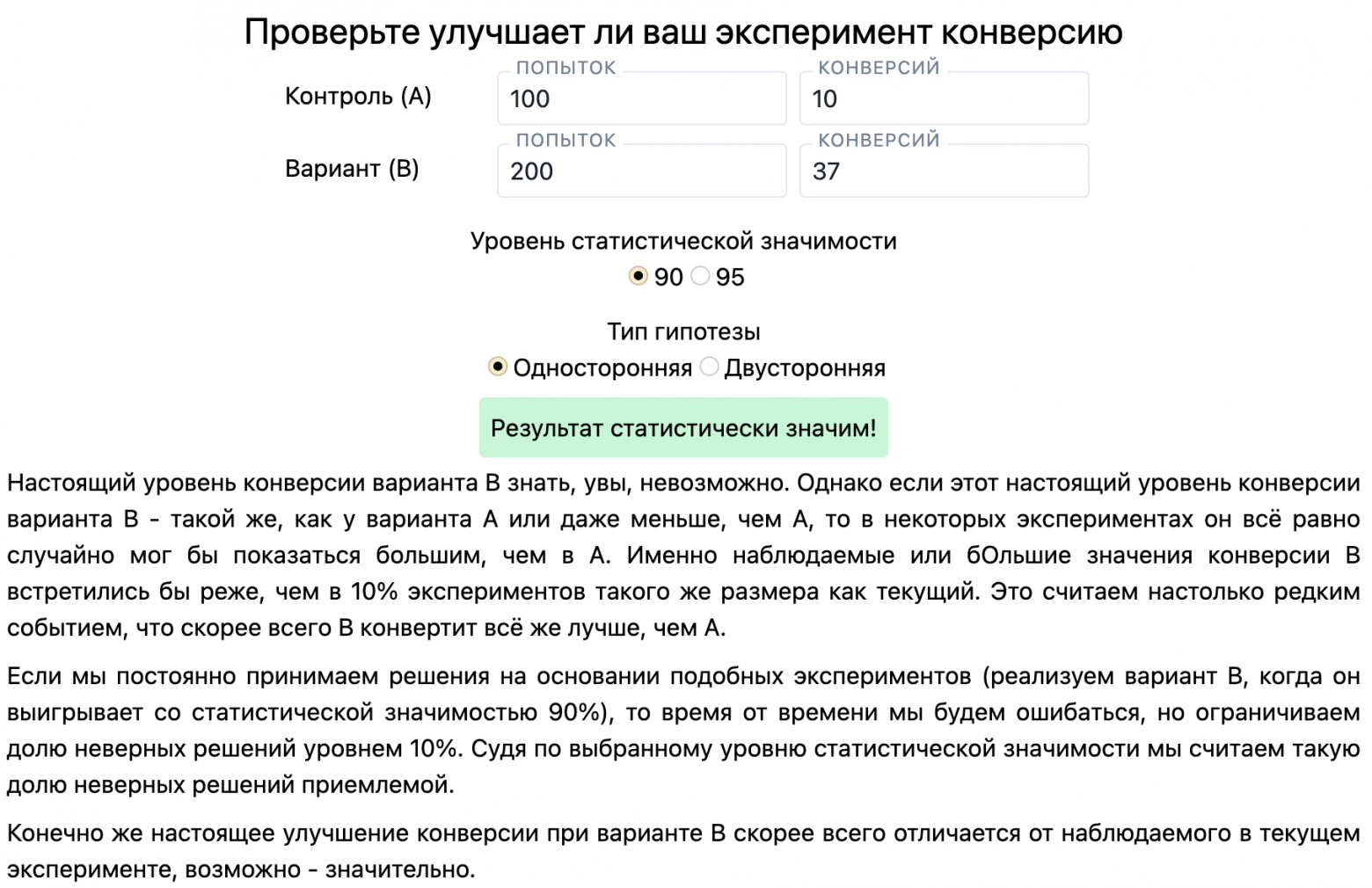
Конечно же интерпретируйте результаты завершившихся тестов с помощью калькулятора, который правильно формулирует результаты. Например, с помощью productab.com, сделанным вашим покорным слугой
Прикиньте стоимость ошибок экспериментов разного рода именно для вашего сервиса и выберите несколько стандартных или не очень стандартных правил. Например, вида:
"Эксперименты с возможной потерей клиентов тестируем с уровнем значимости 95%"
"Просто обычные небольшие улучшения тестируем с уровнем значимости 90%"
"Мелочи, вроде текстов и цветов в местах не касающихся оплаты товара, тестируем c 80%-тной значимостью и если калькулятор рекомендует длину эксперимента больше недели, то пропускаем тестирование совсем"
Ну и конечно, набирайте больше опыта, узнавайте пользователей лучше, чтобы инвестировать в эксперименты, которые на самом деле могут что-то улучшить. Возможно в эксперименты, меняющие весь процесс использования сервиса радикально. Например, что если в нашем воображаемом сервисе вообще отказаться от регистрации и принимать оплату от любого незарегистрированного посетителя, у которого есть банковская карта?
Благодарности
Эта статья увидела свет также и благодаря неравнодушным людям, любезно согласившихся прочесть и прокомментировать черновик, - благодаря Светлане Марченко и Михаилу Марченко, Максиму Стаценко и Даше Стаценко, Саше Лыскову.
А как вы интерпретируете результаты AB-теста?
Насколько масштабный у вас продукт, как вы проводите тесты и выбираете уровень статистической значимости? Автор будет очень благодарен за советы по более понятной интерпретации результатов теста.