Как образуются астрофизические кротовые норы и как мы можем их наблюдать

Любой вопрос или замечания Вы можете написать в комментариях. Также я открыт для личного диалога в телеграме или беседы в нашем чате. А еще у меня есть телеграм-канал о космологии.

Введение

Червоточины, кротовины или кротовые норы (англ.: Wormholes) — это гипотетические пространственно-временные структуры с нетривиальной топологией (см. примечание 1), соединяющие либо две области одной вселенной, либо две разные вселенные (см. рис. 1). Входы в червоточину называются "устьями", а область между "устьями" (mouth) именуют "горлом" (throat). Простейшая конфигурация кротовой норы представляет собой два устья, соединенных одним горлом. Возможны и более сложные структуры кротовин [1].

Примечание переводчика 1: Тривиальной топологией называют ту топологию, которая обладает минимальным возможным количеством открытых множеств, т.е. пустого множества и всего пространства. Если предположить, что существуют две разных вселенные, обладающие топологией сферы и соединяющиеся между собой только одной кротовой норой, то такое пространство-время будет обладать тривиальной топологией сферы. Если же кротовиной соединяются между собой две разные части одной вселенной, то такое пространство-время будет обладать уже нетривиальной топологией тора. Если две вселенные, обладающие топологией сферы, соединяются между собой двумя и более кротовыми норами, то результирующее пространство-время также будет обладать нетривиальной топологией. Система вселенных, соединенных между собой несколькими кротовыми норами, также будет обладать нетривиальной топологией.

Рис.1: Если представить наше трехмерное пространство в виде двухмерной поверхности, то червоточина может быть представлена в виде цилиндрической поверхности, соединяющей две области в одной вселенной или двух разных вселенных. Входы в червоточину называются ее устьями, они соединяются горлом.

Червоточины не являются предсказанием ни одной теории гравитации, в т.ч. ОТО, и об их существовании можно делать лишь предположения, основанные на том, что кротовые норы представляют собой пространственно-временные структуры, существование которых вероятно в искривленных пространствах. Механизм образования и существования этих структур описывается в зависимости от конкретной теории гравитации по-разному — отсюда и исходят проблемы существования червоточин в нашей Вселенной.

Первые попытки решить проблему кротовых нор относят к Эйнштейну и Розену (см. раздел "Формирование..."), [2], а сами червоточины впервые были рассмотрены Мизнером и Уилером в 1957 году [3]. Существуют так называемые "проходимые" и "непроходимые" кротовины и особый интерес к себе привлекают именно проходимые — это те, которые можно пересекать в обоих направлениях, т.е. те, которые являются коротким путем для путешествий на большие расстояния без нарушения скоростного предела. В ОТО проходимые червоточины допустимы лишь при наличии экзотического вида материи, чтобы устья кротовых нор постоянно были открыты — в противном случае червоточина будет схлопываться и закрывать свои устья [6-8], вероятно, превращаясь в обычную черную дыру. В других теориях гравитации надобности в экзотической материи нет [11-14].

Поскольку мы не можем быть уверены в абсолютной правильности теории относительности для нашей Вселенной, то можем предполагать, что проходимые червоточины могут существовать и без специального вида материи. Астрофизические наблюдения могут искать кротовые норы, и за последние тридцать лет сформировалось несколько гипотез их поиска во Вселенной, которые стали особенно актуальны в последние годы, связанные со стремительным прогрессом средств наблюдений, способствующих изучению и поиску новых методов наблюдений кротовин.

В данном материале будут рассмотрены основные методы поиска макроскопических проходимых червоточин. Сначала будут описаны основные механизмы формирования и стабильности проходимых кротовых нор, затем будут рассмотрены сами методы их поиска и наши успехи, связанные с этими методами.

Формирование макроскопических проходимых кротовых нор

Для существования таких объектов как червоточины требуется наличие астрофизических механизмов, способных к созданию этих структур и поддержанию их стабильности на достаточно долгом промежутке времени, ограниченном временем их обнаружения. В классической общей теории относительности существование таких механизмов ограничено топологической цензурой (см. приложение 2). Тем не менее квантовые эффекты позволяют нам обойти эту цензуру.

Примечание переводчика 2: Принцип топологической цензуры гласит о том, что при отсутствии некоей экзотической формы материи во вселенной, описываемой Общей теорией относительности, нетривиальная топология пространства-времени не может быть обнаружена сторонним наблюдателем, так как время коллапса ее областей намного меньше времени, требуемого свету для пересечения этих областей.

Решение проблемы непроходимых червоточин, мост Эйнштейна-Розена

Рассмотрим черную дыру в статической метрике:

Применив преобразование координат:

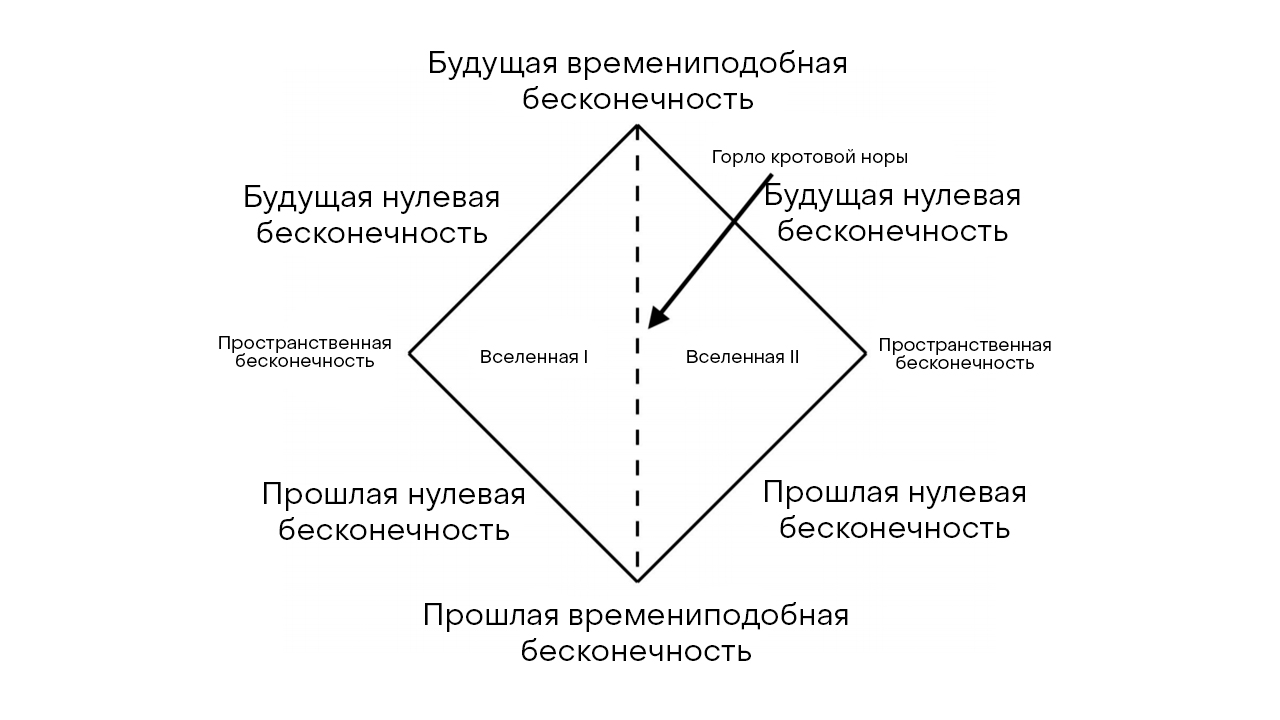
получим метрику, содержащую два несвязанных асимптотически плоских пространства с общим горизонтом. Такая червоточина является необратимой, содержит горизонт событий и может соединять только области двух различных вселенных (см. рис. 2). Проблема заключается в том, что расстояние между устьями у такой червоточины бесконечно, следовательно, устья не могут взаимодействовать за пределами червоточины. Другая проблема состоит в том, что горло кротовой норы определяется распределением массы, потому почти всегда оно будет неустойчиво к малейшим возмущением, за чем будет следовать разрушение под собственной силой тяжести. Для предупреждения этого требуется наличие отталкивающей силы, удерживающей червоточину от разрушения. Неизвестно, возможно ли создать такую кротовую нору, так как мы все еще не знаем, как концентрировать энергию отрицательной плотности в макроскопических объемах. Другим способом обеспечивать стабильность кротовины является ее очень тонкое горло, разрушение которого маловероятно уже при наличии небольшого количества энергии отрицательной плотности.

Рис.2: Диаграмма Пенроуза для червоточины Эйнштейна-Розена. Горло червоточины (горизонт), представлено двумя пунктирными линиями (см. приложение 3). Примечание: уместно заменить термин нулевой бесконечности на термин изотропной бесконечности или светоподобной бесконечности (от англ.: null infinity).

Примечание переводчика 3: Форма записи метрики пространства-времени определяется выбором системы координат. Диаграмма Пенроуза описывается системой координат, где неограниченная вселенная изображается в ограниченной области, а граница называется бесконечностью, так как состоят из точек, бесконечно удаленных во времени. Изобразим в ограниченной области геодезические кривые — каждая из них упрется в две точки на границе, где первая точка будет пределом, к которому стремится точка на геодезической, когда время стремится к минус бесконечности (прошлая бесконечность), а вторая будет пределом, к которому стремится точка на геодезической, когда время стремится к плюс бесконечности (будущая бесконечность). Бесконечность бывает времениподобная (time-like), светоподобная (null) и пространственноподобная (spatial), в зависимости от того, каким является касательный вектор у соответствующей геодезической.

Механизм образования червоточин

Очевидным источником образования кротовых нор является квантовая гравитационная фаза ранней Вселенной, в которой флуктуации топологии пространства-времени позволили бы образование червоточины. С другой стороны, те же флуктуации способствуют образованию областей с отрицательной плотностью, которые обеспечивают стабильное состояние червоточины. Из микроскопических масштабов с ходом расширения Вселенной такие области становятся макроскопическими, а значит потенциально наблюдаемыми. Та же аналогия распространяется на суперструнную теорию, где суперструны с ростом размеров Вселенной растягиваются до больших суперструн и поддерживают стабильность кротовин.

В литературе существует множество моделей голографической вселенной, в которой 3+1-мерное пространство или брана встроено в пространство более высокой размерности [27-29]. Брана по своим свойствам не обязательно прямая: она может изгибаться, скручиваться и даже пересекать себя, а потому точки пространства на такой бране могут быть удалены на большие расстояния вдоль самой браны, но иметь короткий путь в объемлющем пространстве. Если рассмотреть две параллельные браны, относящиеся к разным вселенным, и поместить на них по черной дыре, то мы можем попробовать образовать червоточину, заставив искривить пространства-времена так, чтобы браны соприкоснулись. Такая конструкция, при условии массивных устьев, минимизирует потребность в экзотическом виде энергии для стабильного существования кротовой норы, но может случиться, что длинное горло начнет фрагментироваться на более мелкие части для того, чтобы минимизировать свою энергию.

Поиск астрофизических червоточин

Большинство кротовых нор, рассмотренных в литературе, являются имитациями черных дыр, потому нам требуется различать черные дыры и кротовины. Заметим, что некоторые червоточины могут не являться имитациями черных дыр: например, могут не иметь положительной массы, а следовательно, и аккрецирующей материи вокруг них. Тем не менее такие структуры оказывают влияние на свет (см.: микролинзирование).

А. Гравитационное линзирование

Самый очевидный способ обнаружения червоточин, основанный на поиске событий микролинзирования. Он рассмотрен в работах как первая попытка обнаружения червоточин [33, 34]. В работе Торреса показано, что определенные червоточины могут производить такие события микролинзирования как гамма-всплески; на основании этого авторы определили верхний предел плотности массы кротовиноподобных объектов во Вселенной [35].

Рис.3: Эволюция интенсивности фонового источника при прохождении червоточины с эффективной отрицательной массой (слева) и нормального компактного объекта (справа). Кривые соответствуют значениям параметров воздействия; наименьший параметр воздействия характеризуется более выраженной модуляцией интенсивности источника и наоборот: от зеленого до красного. Иллюстрация взята из [34].

Рис.4: Верхние границы доверительных вероятностей для плотности числа червоточин Эллиса во Вселенной (68% и 95%). Данные поиска квазаров Слоановского цифрового обзора. По оси абсцисс: радиус горла червоточины в единицах парсек/h, где h — масштабный коэффициент Хаббла. Иллюстрация взята из [55].

Рис.5: Диаграмма Пенроуза для червоточины, соединяющей две вселенные (раздел «Вращающиеся звезды»).

Б. Вращающиеся звезды

При условии гладкого соединения двух пространств проходимой червоточиной объекты одного пространства, находящиеся в окрестности первого устья, будут испытывать влияние объектов, находящихся в окрестности второго устья из другого пространства. Это предоставляет нам интересную возможность наблюдать за вращающимися вокруг черных дыр (потенциальных устьев) звездами и обнаруживать наличие постороннего воздействия на них.

Смоделируем проходимую червоточину, у одного устья которого находится тестовый объект (или наблюдатель), а у другого — источник возмущений гравитационного поля (ориг.: «perturber»). Устья располагаются в шварцшильдовских пространствах-временах областью радиуса R такого, чтобы он превышал гравитационный радиус устья, т.е. R > rg ≡ 2GM. Выведя гравитационные возмущения perturber'а мы сможем определить дополнительное ускорение наблюдателя в нашем пространстве-времени:

где µ — масса источника возмущений из другого пространства-времени, A — радиальное расположение этого источника, r — радиальное расстояние от наблюдателя до центра червоточины. Для извлечения наблюдательного эффекта рассмотрим эллиптическую орбиту источника возмущений:

Если орбита объекта вытянута так, что r_a > r_p, то можем выразить эту величину как:

Рассмотрим конкретный пример — звезду S2, вращающуюся вокруг центра нашей галактики Sgr A*, где расположена сверхмассивная черная дыра с M = 4 × 10⁶ M_солн. Масса звезды S2 составляет 14M_солн, ее орбитальный период составляет 15,9 лет и большая полуось имеет размер 1031,69 астрономических единиц. Ускорение звезды составляет 1,5 м/с² и измерено с точностью 4 × 10^-4 м/с². На рисунке ниже показано, с какой точностью возможно исключить ситуацию, в которой подобная звезда на другом конце червоточины (если мы предположим, что Sgr A* является таковой) воздействует на S2 на расстоянии нескольких гравитационных радиусов. Для точности определения воздействия источника возмущений на другой стороне нам нужно исключить все консервативные объяснения, такие как возмутители на нашей стороне или релятивистские эффекты высшего порядка.

Рис.6: График ограничений на массу µ (ось ординат, массы Солнца Mс) и радиуса перицентра rp (ось абсцисс, 2GMс) для гипотетической звезды, вращающейся вокруг Sgr A* с обратной стороны червоточины и возмущающей орбиту S2 на нашей стороне. Линии представляют собой ограничения с точностью ускорения S2, равной 4×10^−4 м/с*с, 2×10^−5 м/с*с и 10^−6 м/с*с соответственно.

Прямой способ наблюдения эффекта дополнительного ускорения — поиск отклонений орбиты объекта от ожидаемого невозмущенного кеплеровского или общего релятивистского значения. Подробно, с учетом расчета дополнительных периодических изменений орбитальной скорости объектов, это было рассмотрено в [62]. Чтобы оценить изменение орбитальной скорости, вызванное дополнительным ускорением, мы можем предположить, что оное происходит раз в орбитальный период источника возмущений с другой стороны червоточины T₀. Мы представляем себе воздействие источника на наблюдателя как импульсивное и происходящее вблизи перицентра. Сравнивая ошибку измерений изменения скорости с дополнительным ускорением, мы можем определить верхний предел массы источника возмущений:

где r_avg — среднее расстояние наблюдаемого объекта от червоточины (большая полуось), f₀ = r'_p/r'_a, σ_v — неопределенность измерения скорости. Поскольку из законов Кеплера следует, что T₀ ∝ r'_p^3/2 этот предел ∝ r'_p^1/4.

Очевидно, что нам нужно подбирать «чистые» системы без динамических изменений, вызванных чем-либо посторонним кроме источника возмущений. Например, для черной дыры с R = 10⁶ м и радиусом орбиты ∼ 106 r_g предел массы источника возмущений должен быть на ∼ 4 порядка ниже, чем полученный из наблюдений S2 за год.

В. Визуализация тени червоточины

Попытки визуализировать сверхмассивные черные дыры и их т.н. «тени» начались более 20 лет назад [71]. Граница тени черной дыры соответствует сфере захвата фотонов и ее анализ таким образом может ограничить геометрию пространства-времени вокруг компактного объекта [72]. Исследование природы сверхмассивных черных дыр на основе изучения их тени стало весьма актуальным после публикации изображения тени черной дыры в центре галактики M87, полученного в рамках проекта Event Horizon Telescope Collaboration [16].

Большинство пространств с червоточиной имеют сферу захвата фотонов за пределами их устьев. Если кротовина окружена каким-либо тонким излучающим газом, то наблюдатель сумеет увидеть тень кротовины. В работе [73] было проведено первое исследование тени кротовой норы, где было отмечено, что размер тени кротовой норы может значительно отличаться от тени черной дыры из-за различного изгиба света (см. рис. 7). Происходит это потому, что проходимые червоточины не имеют горизонта и их гравитационное поле слабее, чем поле черных дыр, потому ожидаемо, что и размеры тени и области захвата фотонов меньше, чем у черных дыр.

Предположив, что граница червоточины представляет собой круг и что нам известны спин и угол наклона черной дыры и потенциальной червоточины, полученные в ходе независимой оценки, мы можем сравнить потенциальную червоточину и черную дыру. Осесимметричная червоточина всегда будет иметь тень в форме деформированной окружности. Такой тест мы можем провести и для анализа изображения сгустка плазмы, аккрецирующего вокруг сверхмассивного объекта (будь то червоточина или черная дыра) [83]: в этом случае видимое изображение материала будет разным из-за различия в изгибе света в пространстве около червоточины или черной дыры.

Еще один тест основан на внутренних свойствах проходимых кротовин — он предоставляет возможность обнаружить излучение, испускаемое с другой стороны червоточины [84, 85]. Такой тест действительно способен отличить червоточину от черной дыры. Заметим, что современные методы визуализации работают на миллиметровой длине волны, потому наблюдать оптическое изображение источника по ту сторону горла червоточины не представляется возможным.

Г. Спектр аккреционного диска

Анализ свойств излучения, испускаемого из внутренней части аккреционного диска вокруг компактного объекта потенциально может стать успешным инструментом для исследования природы источника. Наилучшей системамой для такого анализа является система с геометрически тонким и оптически толстым аккреционным диском, т.е. тем диском, у которого аккрецирующий материал имеет большой угловой момент.

Компактный объект представлен черным кругом с аккрецирующим диском на рис. 7. Каждая точка на диске находится в локальном тепловом равновесии и имеет спектр, подобный спектру черного тела. Весь диск имеет многотемпературный спектр черного тела. Для компактных объектов со звездной массой (M ∼ 10 M_с) спектр будет иметь пик в рентгеновском диапазоне (0,1-1 кэВ), а для сверхмассивных объектов (M ∼ 10⁵-10¹⁰ M_с) — в ультрафиолетовом (1-100 эВ). Тепловые фотоны диска могут подвергаться комптоновскому рассеиванию на свободных электронах в т.н. «короне», представляющей собой более горячее (T_e ∼ 100 кэВ) электронное облако в области сильной гравитации компактного объекта. Часть рассеянных фотонов могут создавать дополнительное освещение аккреционного диска, а само рассеяние и поглощение с последующей флуоресцентной эмиссией создают отражательный компонент [90].

Рис.7: Смоделированное изображение оптически тонкой области излучения для черной дыры Шварцшильда (слева) и проходимой сферически-симметричной червоточины (справа). Координаты осей абсцисс и ординат указаны в единицах гравитационного радиуса системы. Иллюстрация взята из [73].

Рис.8: Компактный объект с аккрецирующим геометрически тонким и оптически толстым диском. Иллюстрация взята из [89].

Исследования конкретных решений червоточин представлены в работах [91-94]. Однако существует два факта, которые необходимо принимать во внимание при использовании данного метода обнаружения кротовых нор. Во-первых, метод работает только для компактных объектов со звездной массой, т.к. для сверхмассивных объектов с максимумом излучения в УФ-диапазоне поглощение пыли ограничивает возможности для точного измерения спектра диска. Во-вторых, тепловой спектр диска имеет простую форму, в результате чего при анализе реальных данных мы обнаружим сильное вырождение параметров, что ставит под сомнение возможность отличить черную дыру от червоточины [95].

Стоит отметить и то, что в случае проходимых червоточин можно ожидать, что часть материала может перетекать по горлу из одного устья в другое, что может создать движение вещества в противоположных направлениях, а, следовательно, и генерирование гамма-вспышек [103].

Д. Гравитационные волны

Гравитационно-волновые тесты представляют собой еще один подход к поиску астрофизических червоточин. В отличие от электромагнитных тестов, зависящих от метрики пространства-времени и упомянутых ранее, гравитационно-волновые тесты требуют еще и вычисления сигнала гравитационной волны из уравнений теории, поэтому необходимо уточнить, какую гравитационную модель мы будем брать за основу.

Рис.9: Эволюция деформации, разделения черной дыры и ее относительной скорости для события GW150914 со временем. Иллюстрация взята из [15].

Эксперименты LIGO и Virgo в настоящее время достигли чувствительности, позволяющей обнаружить слияние двух компактных объектов звездной массы каждые несколько дней. Коалесценция состоит из трех стадий: движения по спирали, слияния и финальной стадии. На стадии движения по спирали два тела вращаются вокруг общего центра масс, теряя свою энергию и угловой момент за счет излучения гравитационных волн. Расстояние между телами уменьшается, а относительная скорости и частота обращения увеличивается. На фазе слияния образуется один объект. После слияние следует финальная стадия, в которой образовавшийся объект излучает гравитационные волны, чтобы прийти к равновесной конфигурации.

Перед фазой слияния два объекта находятся относительно далеко друг от друга, а само сближение занимает слишком малый промежуток времени для того, чтобы провести точное измерение геометрии пространства-времени. Это легче сделать, если массы двух объектов значительно различаются, например, как в работе [104], где авторы рассматривают черную дыру массой 5M_с и червоточину массой 200M_с. Подобная система нами еще не наблюдалась, но, вероятно, она будет обнаружена в будущем, например, в связи с использованием космических гравитационно-волновых антенн (типа eLISA). Червоточины могут иметь очень разные приливные свойства и даже могут порождать периодические всплески после стадии слияния [105]. Вообще фаза слияния потенциально информативна для определения природы компактного объекта и проверки теории гравитации, но все еще неприступна из-за необходимости в точных и продолжительных измерениях сигнала и сложности делать теоретические предсказания.

Излучение гравитационных волн в стадии слияния и финальной стадии характеризуется так называемыми квазинормальными модами (KHM), которые в зависимости от конкретной модели могут предоставить информацию о природе компактных объектов [107-113]. Текущие гравитационно-волновые данные еще не в состоянии проверить эти модели, поскольку необходимы точные измерения по крайней мере нескольких KHM, что достижимо в обозримом будущем.

Заключение

Существование проходимых червоточин во Вселенной — это экзотическая и увлекательная гипотеза, которая на данный момент представляет единственную возможность для межзвездных и межгалактических путешествий в далеком будущем. В последние годы произведен большой прогресс в исследованиях компактных объектов, что побуждает к новым исследованиям и проверкам природы компактных объектов в ближайшем будущем. К сожалению, нам не удалось процитировать и обсудить все материалы из области изучения кротовых нор. Тем не менее, мы надеемся, что этот обзор послужит в качестве отправной точки для заинтересованного читателя в изучении этого увлекательного направления астрофизических исследований.

Комментарий переводчика

Оригинальная статья 2105.00881 (gr-qc) Козимо Бамби и Деяно Стойковича была представлена на arXiv.org 3 мая 2021 года, последнее изменение от 8 мая 2021 года. Цитата из обзора препринтов astro-ph Сергея Б. Попова: «Обзор посвящен астрофизическим поискам червоточин. Конечно, маловероятно, что они встречаются в природе, тем не менее интересно узнать, как бы они могли проявляться, и какие наблюдательные пределы на эти проявления имеются. Кроме того, статья начинается с понятного физико-исторического введения». Все материалы, использованные в качестве источников к этому материалу, представлены в конце оригинальной статьи.

Ну и напоминаю, о том, чтобы читатель не стеснялся задать вопрос или поправить меня в комментариях. Также у меня есть телеграм-канал, где я рассказываю о последних новостях космологии и астрофизики, а также пишу об астрофотографии. Пишите мне в личку или наш чат. Всем добра!