Казалось бы, что можно добавить на тему о популярной задачке о расстановке ферзей на шахматной доске стандартной размерности 8x8 клеток? Но как оказалось и тут можно внести свою толику программистской мысли.
Классически задача решается последовательным перебором ферзей на заданной линии и бонусом предлагается анализировать диагонали которые покрываются установкой ферзя в нужную клетку. Но те реализации алгоритмов, что я видел, установкой или снятием ферзя с маркировкой диагоналей, едва ли перекрывают по быстродействию расстановку ферзей по-принципу ладьи.
Как оказывается в алгоритм можно привнести существенные улучшения отказавшись от линейного обхода/перебора клеток и внеся понятие анализа состояния атак шахматной доски.
Я добавил два улучшающих принципа в алгоритм, которые позволяют снизить общее кол-во переборов в три раза.
Двигаемся по столбцам (A-H). В столбцах перебираем строки (1-8)
Установить ферзя, означает - промаркировать все атаки (горизонтальную и диагональные) и пометить столбец с ферзём, как занятый.
Снять ферзя, означает снять маркировку атак и пометить столбец, который он занимал, как свободный.
Проверить поставлены ли все ферзи во всех столбцах. Если да, то выдать удачный результат.
Вернуться на шаг назад в переборе (снять последнего установленного ферзя).
Рекурсивно переходим к пункту №1.Проверить, есть ли такой свободный столбец, в который нельзя поставить ферзя?. Если такой столбец имеется - шаг назад в рекурсивном обходе, дальнейшие ходы - бессмысленны.
Вернуться на шаг назад в переборе (снять последнего установленного ферзя).
Рекурсивно переходим к пункту №1.Проверить, есть ли такой свободный столбец в который можно поставить только одного ферзя? Если такой такой имеется, разумеется туда и ставим ферзя, жертвуя линейностью обхода. Рекурсивно переходим к пункту №1.
Находим ближайший к началу доски свободный столбец, выполняем в нем перебор всех не атакованных позиций. Устанавливаем ферзя в не атакованную позицию.
Рекурсивно переходим к пункту №1
Для реализации алгоритма я выбрал 64-х битную математику в арифметических и логических операциях. [ + - AND NOT XOR OR << >>].
Шахматная доска 8x8 в 64 клетки отлично ложится в 64-х битовую переменную.
Чтобы не использовать внутренние циклы для маркировки состояний по диагонали, я инициализирую их заранее. Есть три раздельных слоя для маркировки атак ферзя. Два диагональных слоя и один горизонтальный. В один слой все три атаки сливать нельзя, так как это не позволит восстановить предыдущее состояние шахматной доски.
Для демонстрации своего алгоритма я выбрал язык C#, как наиболее легкий и понятный. JS не содержит поддержки целочисленной 64-х битной арифметики, и чтобы не усугублять демо-пример кластеризацией на 32-х битную арифметику - я от него отказался.
Язык СИ несколько тяжелей, по тексту, но содержит поддержку нужных для ускорения работы алгоритма инструкций процессора - POPCNT и BSF в виде "intrinsics"-функций.
С JVM на момент написания этой статьи существуют некоторые неопределённости, о которых не будем распространяться.
В итоге выбран C# с дополнительным классом битовой логики, который пытливый программист сам может переложить на процессорную аппаратную поддержку.
Итак приступим!
Размещаем шахматную доску в 64-битную переменную следующим образом

Первого ферзя в алгоритме ставим на [A1] (x = 0, y = 0). Базовое движение делаем по X-оси (по столбцам), на каждой оси перебираем позицию Y (строки). Как видно из иллюстрации, каждый столбец представляет из себя байт (8-мь бит).
Теперь промаркируем диагонали:
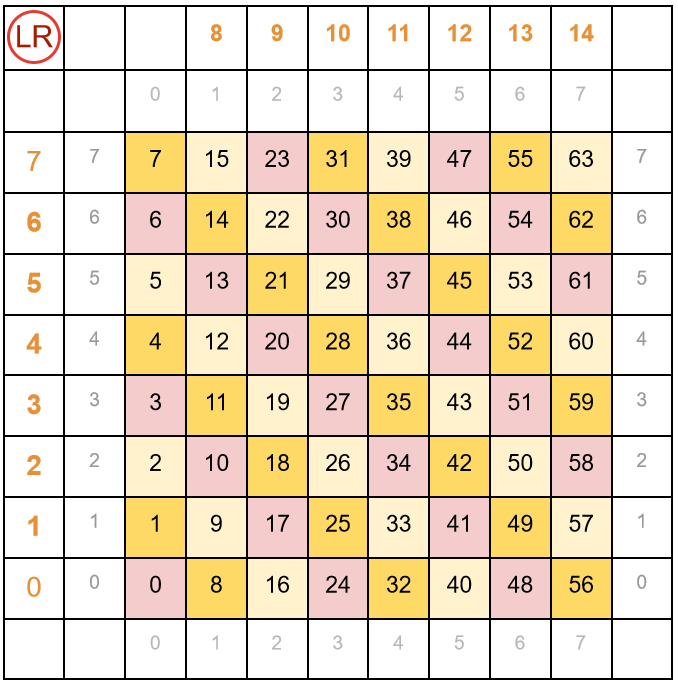
Номер LR-диагонали считается по формуле: N = X+Y
Так например, для позиций (xy): 3:2 (26), 4:1 (33), 1:4 (12) - Номером диагонали будет - 5;
для позиций (xy): 7:4 (60), 5:6 (46), 4:7 (39) - Номером диагонали будет - 11;
Диагональ LR: (LEFT+BOTTOM : RIGHT+TOP)

Номер RL-диагонали считается по формуле: N = 7 - X+Y
Ну а дальше - дело техники:
Вводим массивы:
ulong diag_LR[15]
ulong diag_RL[15]
Массивы содержат шахматную доску где биты установленные в 1 означают атаку по диагонали. Предварительно инициализируем их. Данные массивы нужны для того, чтобы не вводить в основной цикл внутренние циклы для маркировки атак. Массив для горизонтальной атаки не нужен, поскольку легко накладывается 64-битным числомВводим переменную "ulong markers". Каждый байт markers содержит либо 0x00, либо 0xFF, чтобы обозначать доступен ли X-столбец для установки ферзя.
0xFF - доступен
0x00 - занятВводим три переменные (ulong): attacks_HZ, attacks_LR, attacks_RL, чтобы держать состояния атак по горизонтали и вертикалям. Чтобы получить полное состояние всех атак клетки, надо слить их по операции OR: attacks_HZ | attacks_LR | attacks_RL.
Для понимания работы алгоритма надо также понимать, что часть операций над 64-х разрядными числами можно совершать параллельно над байтами числа, если числа хранимые в байтах не вызывают арифметического переполнения относительно друг-друга. Например число 0x0303_0303_0303_0303 - можно рассматривать, как вектор из 8-ми байтов установленных в 3-и. Тогда операцией инкрементации вектора будет прибавление к числу - значения 0x0101_0101_0101_0101. Результатом будет - 0x0404_0404_0404_0404.
Ответом на вопрос - "В байт векторе присутствуют байты со значениями в диапазоне от 0 до 8. Есть ли в байт-векторе, хотя бы одно число 8?" - будет наложение на вектор маски - 0x0808_0808_0808_0808 операцией AND. Ненулевое значение означает, что байт-векторе есть такие числа.
0x0108_0304_0708_0506
AND
0x0808_0808_0808_0808 =
-----------------------------------
0x0800_0000_0008_0000 - ЕСТЬ (ненулевой результат)
0x0106_0304_0700_0506
AND
0x0808_0808_0808_0808 =
-----------------------------------
0x0000_0000_0000_0000 - НЕТ (нулевой результат)
Код прототипа:
Выражения предельно упрощены, для понимания логики происходящего, и для трассировки алгоритма в отладочном режиме
Алгоритм оптимизирован под инструкцию процессора BSF (Bit Scan Forward), которая в прототипе дана, как функция "BitOp.bsf64()". Также может применяться инструкция процессора
BLSR(BMI1).
using System; namespace Queen_8x8 { delegate void Solution(int[] queens); class Program { static void Main(string[] args) { print("Hello Queens!"); print(":"); Queen_8x8 task = new Queen_8x8(); task.smart_check = true; task.init(print_solution); task.run(); print("solution_count = " + task.solution_count); print("solve_count = " + task.solve_count); print("reverse_count = " + task.reverse_count); } static void print(String s) { Console.WriteLine(s); } static void print_solution(int[] queens) { String s = ""; s += "[ "; for (int i = 0; i < queens.Length; i++) { s += Char.ConvertFromUtf32(i + 65) + (queens[i] + 1).ToString(); if (i < (queens.Length - 1)) s += ", "; } s += " ]"; print(s); } } class Queen_8x8 { protected Solution solution; public const int queens_count = 8; public const int diag_count = queens_count * 2 - 1; public ulong markers = 0xFFFF_FFFF_FFFF_FFFF; public int[] queens = new int[queens_count]; ulong[] diag_LR = new ulong[diag_count]; ulong[] diag_RL = new ulong[diag_count]; ulong attacks_HZ = 0; // атака по горизонтали ulong attacks_LR = 0; // атака по диагонали BL-TR [\] ulong attacks_RL = 0; // атака по диагонали BR-TL [/] public bool smart_check = true; // Statisticks public int solution_count = 0; public int solve_count = 0; public int reverse_count = 0; private int get_LR(int x, int y) { return x + y; } private int get_RL(int x, int y) { return (queens_count - 1 - x) + y; } public void init(Solution solution) { this.solution = solution; solution_count = 0; solve_count = 0; reverse_count = 0; markers = 0xFFFF_FFFF_FFFF_FFFF; for (int i = 0; i < queens.Length; i++) { queens[i] = -1; } for (int i = 0; i < diag_count; i++) { diag_LR[i] = 0; diag_RL[i] = 0; } for (int x = 0; x < queens_count; x++) { for (int y = 0; y < queens_count; y++) { ulong mask = 1UL << ((x << 3) + y); diag_LR[get_LR(x, y)] |= mask; diag_RL[get_RL(x, y)] |= mask; } } } public void run() { solve(); } protected void step(int qx, int qy) { ulong q_CM = 0xFFUL << (qx << 3); ulong a_HZ = 0x0101_0101_0101_0101UL << qy; ulong a_LR = diag_LR[get_LR(qx, qy)]; ulong a_RL = diag_RL[get_RL(qx, qy)]; // Set Queeen queens[qx] = qy; markers &= ~q_CM; attacks_HZ |= a_HZ; attacks_LR |= a_LR; attacks_RL |= a_RL; // Recurse solve(); // Remove Queeen attacks_HZ &= ~a_HZ; attacks_LR &= ~a_LR; attacks_RL &= ~a_RL; markers |= q_CM; queens[qx] = -1; } protected void solve() { if (markers == 0) { solution_count++; solution(queens); return; } ulong attacks = attacks_HZ | attacks_LR | attacks_RL; // Получаем в каждом байте 64-разрядного числа - // сумму занятых мест по столбцам // Каждый байт обозначает столбец таблицы и содержит число // в интервале от 0 до 8 ulong sum_vec_8 = BitOp.popcnt64_bv(attacks); // Проверка, что остались незаполненные столбцы // Определяем что в каком либо столбце присуствует число 8 // Если в каком-либо столбце присутствует число 8, то общее значение теста // станет ненулевым ulong test = sum_vec_8 & 0x0808_0808_0808_0808UL; test &= markers; // Отбрасывем столбцы (columns), где уже установлены ферзи if (smart_check && test != 0) { return; // Есть столбец не занятый ферзем, но поставить в этот столбец ферзя - невозможно } // Проверка, на то что есть столбцы, только с одим возможным ходом // Поскольку мы отбросили вариант, что в столбцах присутствует число 8 // прибавляем к каждому столбцу единицу и опять проверяем все столбцы на наличие числа 8 // Если изначально в каком-либо столбце присутствовало число 7, то общее значение теста // станет ненулевым test = sum_vec_8 + 0x0101_0101_0101_0101UL; test &= 0x0808_0808_0808_0808UL; test &= markers; // Отбрасывем столбцы (columns), где уже установлены ферзи int qx; int qy; ulong column; if (smart_check && test != 0) { reverse_count++; qx = BitOp.bsf64((test >> 3)) >> 3; column = (~attacks >> (qx << 3)) & 0xFFUL; qy = BitOp.bsf64(column); step(qx, qy); return; } // Делаем перебор по столбцу qx = BitOp.bsf64(markers) >> 3; column = (~attacks >> (qx << 3)) & 0xFFUL; while (column != 0) { solve_count++; qy = BitOp.bsf64(column); column &= column - 1; // BLSR BMI1!!! column &= ~(1UL << qy); // Сбросить самый младший единичный бит step(qx, qy); } return; } } class BitOp { // Просумировать все биты в байтах 64-разрядного числа public static ulong popcnt64_bv(ulong value) { ulong result = value; result = result - ((result >> 1) & 0x5555_5555_5555_5555UL); // Результат сумм по 2-а бита result = (result & 0x3333_3333_3333_3333UL) + ((result >> 2) & 0x3333_3333_3333_3333UL); // Результат сумм по 4-е бита result = (result + (result >> 4)) & 0x0F0F_0F0F_0F0F_0F0F; // Результат сумм по 8-ь бит return result; } public static byte add64_bv(ulong value) { ulong result = value; result += result >> 8; // Результат сумм по 16-ь бит result += result >> 16; // Результат сумм по 32-ь бит result += result >> 32; // Результат return (byte)(result); } /* * Подсчитать кол-во битов установленных в 1 в 64-разрядном числе * Полностью эквивалентна машинной инструкции Intel x86/x64 - POPCNT */ public static byte popcnt64(ulong value) { ulong result = value; result = result - ((result >> 1) & 0x5555_5555_5555_5555UL); // Результат сумм по 2-а бита result = (result & 0x3333_3333_3333_3333UL) + ((result >> 2) & 0x3333_3333_3333_3333UL); // Результат сумм по 4-е бита result = (result + (result >> 4)) & 0x0F0F_0F0F_0F0F_0F0F; // Результат сумм по 8-ь бит result += result >> 8; // Результат сумм по 16-ь бит result += result >> 16; // Результат сумм по 32-ь бит result += result >> 32; // Результат return (byte)(result); } public static byte popcnt8(byte value) { ulong result = value; result = result - ((result >> 1) & 0x55); // Результат сумм по 2-а бита result = (result & 0x33) + ((result >> 2) & 0x33); // Результат сумм по 4-е бита result = (result + (result >> 4)) & 0x0F; // Результат сумм по 8-ь бит return (byte)(result); } public static int bsf64(ulong value) { if (value == 0) return -1; int bitpos = 0; ulong mask = 0xFFFF_FFFF_FFFF_FFFFUL; int step = 64; while ((step >>= 1) > 0) { if ((value & (mask >>= step)) == 0) { value >>= step; bitpos |= step; } } return bitpos; } } }
Результат программы:

В консоли видно эталонное число найденных комбинаций равное 92, и количество переборов равное 672.
В прототипе присутствует флажок-переменная "smart_check". Установка его в FALSE приведет к отключению моей оптимизации. Тогда вывод в консоль станет классическим.
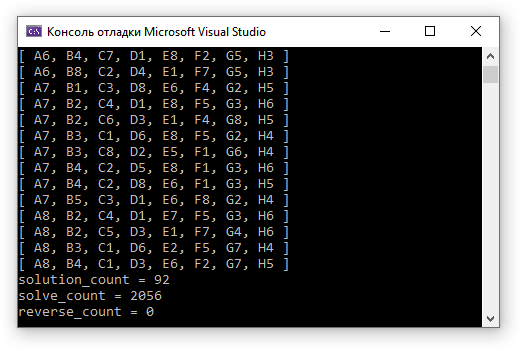
2056 ./ 672 = 3,05
Оптимизация на количестве переборов выше в 3-и раза.
P.S. Продолжение возможно последует...
UPDATE!!! 27/07/2022
P.P.S. Уже появилась уточненная версия алгоритма (1а), где дополнительно анализируются не только колонки, но и строки, на возможность поставить в них ферзя или поставить единственно возможного ферзя. На данный момент вывод результата выглядит, так:

Упало количество ходов перебора (-80) и реверс-шагов (-140).
