Comments 345
Альтернатива без goto № 3: попеременное использование if и (0)
Я даже не догадывался, что язык вообще предоставляет возможность так писать.
Ну switch - это фактически goto на один из case. Код примера, конечно, эзотерически выглядит.
А вот ещё классика: https://en.m.wikipedia.org/wiki/Duff's_device
В языке C, на самом деле, switch-case -- это тот же goto. Поэтому можно писать очень странные вещи, вроде такой:
int main()
{
volatile int n = 3;
for (volatile int i = 0; i < n; i+= 1)
switch (i) case 0: if (0) break; else
{
int r0 = i + 20, r12 = i + 10;
printf("1 %d %d\n", r0, r12);
default:
printf("2 %d %d\n", r0, r12);
}
return 0;
}На ревью за такой код руки сломать могут.
Странно, что не рассмотрели вариант с 2 свичами: в первом выполняется уникальная работа, во втором - общие случаи.
goto - не зло, а просто весьма низкоуровеневый инструмент. Как ассемблерные вставки. Никто не применяет ассемблерные вставки где попало, просто потому что хочется, или потому что не дается структурное программирование? Вот и с goto также. Поэтому, конечно, в низкоуровневых языках, а также в универсальных, претендующих в том числе на системное программирование, оператор goto должен быть, причем у него могут быть и альтернативы, и расширения, что делает этот низкоуровневый инструмент более мощным и полноценным (хотя иногда и более опасным).
Первое - это использование именованных блоков кода и операторов break/continue с именами блоков кода. У каждого блока кода, начинающегося с ключевого слова (if, for, while, switch и т.д.) может быть имя, объявляемое после ключевого слова. Такое имя работает как метка, улучшает читаемость кода и может быть использовано для других целей - зависит от фантазии автора языка программирования. Не знаю в каких реальных языках это есть, но я подобное придумал уже давно:)
Второе - сам синтаксис объявления меток. В С/С++ он архаично-примитивен: имя и двоеточие. Это идеологически неверно, любое объявление должно начинаться с ключевого слова, например "label". Как минимум проще искать метки - и визуально, и с помощью инструментов поиска по тексту.
Третье - локальная видимость меток, т.е. метка, объявленная внутри блока кода, невидима вне этого блока кода (и в более широком смысле - явное управление видимостью меток, с локальной видимостью по умолчанию). Это дает некоторую "защиту от дурака": для выхода из вложенных циклов использовать такие метки просто, для входа куда-то вглубь - уже сложнее. В расширениях GCC это есть: https://gcc.gnu.org/onlinedocs/gcc/Local-Labels.html#Local-Labels
Четвертое - метки-переменные, массивы меток и т.д. Исключительно низкоуровневая возможность, сравнимая только с Ассемблером, в GCC опять же имеется: https://gcc.gnu.org/onlinedocs/gcc/Labels-as-Values.html#Labels-as-Values
По поводу первого - такое есть в Kotlin, очень полезная штука.
Примеры:
outer@ while(/* condition */) {
inner@ while(/* condition */) {
if (error) {
break@outer
}
if(eof) {
break@inner // или просто break
}
}
}
Причём эти метки могут быть ещё и неявные, например, для разрешения неопределённости в каком контексте работает return в inline лямбдах:
fun compute(data: Data): Result {
data.flatMap(/* process */).forEach {
if (it.isSuccess) {
return@compute it // это уже return из всей функции compute, а не из лямбды forEach
}
}
}Можно ещё так:
for ...
for ...
break break;
for ...
for ...
break continue;
...
Был такой proposal для C. Очень простая фича в реализации.
достаточно параметра уровняА если при рефакторинге уберется / добавится цикл? С явными именами надежнее
с именами все-таки получше
Выглядит круто
// это уже return из всей функции compute, а не из лямбды forEach
А если мы эту лямбду вернем из функции в виде возвращаемого значения (она же first-class, значит имеем право?), и затем вызовем отдельно, то куда будет осуществлен return?
А тогда мы не имеем права делать return@compute - он работает только с лямбдой, которая в конечном счёте оказывается встроенной в вызывающую функцию (в данном случае за счёт того, что forEach помечена как inline). Немного туповатый пример, но тем не менее, видно, что при попытке собрать этот код прямо говорится "return is not allowed".
И конечно же в любом языке с hof (я уверен что и в котлине, честно не знаю синтакс) это решается гораздо читабельнее:
data.flatMap(...).first(it.isSuccess)И 99% примеров где нужен такой return или goto решаются каким-либо подобным очень простым и гораздо более читабельным способом.
И достаточно месяцок поупражняться с high order functions в хаскеле чтобы никогда в жизни в голове уже не возникала идея о необходимости раннего выхода, исключения, goto или чего-либо в таком роде.
Спорная штука, обычно это превращается в лапшу и работает только если компилятор может оптимизировать подобные выражения.
Консервативные деды недоверяют оптимизаторам. Ведь как можно гарантировать что код типа vec.iter().reverse().mutate(x=>if(x>0)--x) соберётся как "один итератор" к которому будет применяться все те модификаторы которые мы навешали.
В языках где есть и можно пользоваться goto, это инструмент такого же уровня как mallocate.
Можно сказать что низкоуровневый, можно сказать что обычный.
использование именованных блоков кода и операторов break/continue с именами блоков кода. У каждого блока кода, начинающегося с ключевого слова (if, for, while, switch и т.д.) может быть имя, объявляемое после ключевого слова. Такое имя работает как метка, улучшает читаемость кода и может быть использовано для других целей - зависит от фантазии автора языка программирования. Не знаю в каких реальных языках это есть
Perl.
В С/С++ он архаично-примитивен: имя и двоеточие. Это идеологически неверно, любое объявление должно начинаться с ключевого слова, например "label". Как минимум проще искать метки - и визуально, и с помощью инструментов поиска по тексту.
Зачем? Достаточно конвенции "с начала строки", и прекрасно ищется регэкспом ^.*:
В C/C++ и многих языках пробелы не имеют значения и вся программа может содержаться в одной строке. Так что грамматику разбирать придётся. А в других языках есть многострочные строки-литералы. Там тоже grep не сработает.
в других языках есть многострочные строки-литералыВ C++11 тоже появились сырые строки, так что даже в другие языки ходить необязательно.
А ещё встречал примеры, когда goto-метки отодвигают отступами, чтоб они визуально были в том же блоке, что и соседние строки; как по мне — красивее, чем когда метка «торчит» из блока 3-4 уровней вложенности (особенно если используются классические табы по 8 символов шириной). Впрочем, вкусовщина…
Достаточно конвенции "с начала строки", и прекрасно ищется регэкспом
^.*:
А еще этим регекспом найдутся строковые литералы с двоеточием, комментарии с двоеточием, несколько сотен/тысяч всяких "public:" и "private:", конструкторы со списками инициализации, объявления классов с наследованием, битовые поля, все case в свичах, тернарные операторы и примерно бесконечность обращений через неймспейс.
Зачем? Достаточно конвенции «с начала строки», и прекрасно ищется регэкспом ^.*:Этим регэкспом найдутся вообще абсолютно все двоеточия по всему тексту.
По поводу первого: такое есть и в D (помимо Kotlin)
cycle1: foreach(option; [flag, altFlag]) {
foreach(i, arg; args) {
if (arg == option || arg.startsWith(option~"=")) {
index1 = i;
flag = option;
break cycle1;
}
}
}
Редко приходится пользоваться, но когда приходится — довольно удобно (можно и continue так же использовать).
Плюс в switch-case-конструкциях можно использовать goto для перехода именно
к нужному case, но это совсем не пригождалось.
Вы почти Фортран 2008 придумали.
К счастью, если подняться чуть повыше C, то нужда в
goto отпадает (вот прям почти совсем), спасибо деструкторам.Из «красивого», встреченного в живой природе:
void fn(args) {
... code ...
if (!check1) goto done;
... code ...
if (!check2) goto done;
... code ...
if (!check3) goto done;
... code ...
done:
return;
}
done: и return есть некая очистка (в основном разлочить мьютексы), а в этой — просто goto потому что можем… ну, бываетМогу понять авторов - если в эту функцию кто-то придëт делать рефакторинг или доработку, при которой добавится содержательная обработка ошибок, ему сразу станет понятно, где еë разместить. Единообразие кода способствует его читаемости и поддерживаемости.
Деление на ноль все-таки другое измерение чем goto.
Скорее для консистнетности - если все соседние функции построены в таком духе, то и эту тоже стоит писать как остальные
Ничего красивого, лучше заменить goto done на return.
А если вы готовы задействовать высшую математику, то во многих случаях предельные переходы позволяют находить точное значение a/b где b стремится к нулю. Да, это не «просто взял и разделил», но вся высшая математика такая: то пределы, то бесконечные ряды, то ещё чего похуже…
IEEE 754 так себе модель математикиКак и любая другая модель, со своими достоинствами и недостатками. И всё же я настаиваю, что это корректный пример: деление на 0 определено, и в начальной-средней школе IEEE 754 (обычно) не изучают.
делить на ноль всё ещё нельзя даже тамВикипедия говорит, что бывают алгебры где на ноль таки можно делить: тыц. Понятия не имею, насколько это нишевые конструкции, но как второй пример сгодится.
Ну и всё, что вы по факту делаете — это определяете / как возвращающий не элемент вашей конечной структуры, а Maybe с этим элементом.Я правильно вас понимаю, что так делать нечестно, а вот обычная арифметика, возвращающая
Result при делении (который Err(undefined) если делитель равен нулю) — это нормально?Если да — не вижу смысла продолжать дальше ворочать софистику.
всё, что вы по факту делаете — это определяете / как возвращающий не элемент вашей конечной структуры, а Maybe с этим элементом.
Обычная арифметика не возвращает никаких Result
Зачем вы на ровном месте пытаетесь строить логические парадоксы?
IEEE 754 возвращает конкретное значение при делении на 0 — для вас это всего лишь
Maybe.Обычная арифметика говорит, что на 0 делить нельзя — для вас это не
Err(undefined), это нельзя делить на 0.То есть арифметикам разрешено возвращать потенциально пустое значение, но запрещено возвращать ошибку? А что тогда есть деление на 0 в обычной арифметике, если не ошибка?
Однако, вернёмся к началу треда:
А где на ноль делить можно?Я вам привёл 2 примера (IEEE 754 и алгебраические колёса) — они вас не устроили, потому что… не знаю почему, просто не устроили. Зато вы сами привели некий вырожденный пример, где на 0 делить можно:
Можно проще: в алгебре из одного элемента (назовём его 0) можно делить на 0 без всяких извращений: 0/0 = 0, и все привычные алгебраические свойства выполняются (ну там, ∀x.∀y. (x / y) × y = x как пример).Ваш собственный ответ вам же нравится? Или вы привели пример, который не пример по вашей оценке? В каком месте вы противоречите себе?
У вас нет никакого адекватного сохраняющего структуру мономорфизма из [подмножества] IEEE 754-чисел в нормальные математические вещественные (или рациональные)А почему вы решили, что какие-либо преобразования между разными типами чисел вообще должны существовать? Если к 15 часам прибавить ещё 15 — это будет 30 == 6 часов, потому что модульная арифметика и всё такое. А вот 15+15 в не-модульной арифметике почему-то 30, но не 6. Как вы хотите
30 == 6 записать в терминах обычных вещественных (рациональных) чисел?Что такое «потенциально пустое значение» в контексте арифметических операций, область значений которых, вообще говоря, те же числа?Откуда мне знать, это вы из кроличьей норы вытащили
Maybe. В рамках IEEE 754 любая математическая операция возвращает число, определённое тем же стандартом, ничто никуда не теряется и не становится внезапно IEEE 754-неопределённым.на мой взглядВо-от, с этого и надо было начинать. Зачем вообще приводить примеры, когда они субъективно плохи, и это единственное, что вам важно?
Мой собственный пример мне настолько же не нравится: это не очень интересный объектТо есть вы отвергаете мои примеры, отвергаете свой собственный, потому что оказывается у примеров должны быть какие-то дополнительные, не оговорённые в явном виде свойства помимо "всего лишь соответствовать критериям запроса"? Да это же наглядный пример «без внятного ТЗ результат ХЗ».
Поскольку изначальный запрос был «А где на ноль делить можно?» — IEEE 754 является корректным ответом (как оказалось, даже не единственным). Все ваши дополнительные условия/требования — попытка не принять корректный пример как таковой.
Чтоб избегать подобных бессмысленных дискуссий в будущем, очень прошу вас впредь ко всем просьбам привести примеры добавлять что-то вроде «эти примеры должны также соответствовать любым моим хотелкам, которые могут прийти в голову во время дискуссии», либо сразу указывать полный список требований, и не ожидать от примеров чего-либо сверх указанного списка.
Модульная арифметика не претендует на то, чтобы быть моделью (в широком смысле) обычной арифметики.
Напротив: модульная арифметика в цифровых компьютерах стала наиболее широко (с огромным отрывом) применяемой моделью целочисленной арифметики. Может, вы знаете какую-нибудь более удобную модель, применимую в устройствах с конечной, дискретной, двоичной памятью? Я -- не знаю.
IEEE 754 вроде как косит под то, чтобы быть какой-то моделью вещественной арифметики.
Про неё можно сказать всё то же самое.
По моему, у вас спор слепого с глухим. Вы мешаете в кучу абстрактную математику и численные методы. Которые хоть и работают в целом по общим математическим законом, но все-таки имеют ряд допущений, связанных с реализацией всего это на уровне машинного представления чисел. Где нет понятия "бесконечность", где все, даже NaN есть некоторое представимое в виде набора бит число. И где два числа считаются равными (с точки зрения процессора) если они отличаются не более чем на некоторую предельно малую величину (для процессора опять же). Т.е.
#include <float.h>
...
double a, b;
...
if (a == b) {
// Некорректно!!!
}
if (fabs(a - b) <= DBL_EPSILON) {
// Корректно
}Это распространённое заблуждение о том, как правильно сравнивать числа с плавающей точкой. Для критики такого сравнения - контрпример c малыми числами, между которыми помещается довольно много представимых значений double:
#include <float.h>
#include <math.h>
#include <stdio.h>
int main() {
double a = 1e-16;
double b = 2e-16;
if (a == b)
printf("a == b"); // это условие не выполняется
if (fabs(a - b) <= DBL_EPSILON)
printf("fabs(a - b) <= DBL_EPSILON"); // это выполняется
}
Как корректно сравнивать, зависит от того, что значит "корректно". Некоторые варианты можно посмотреть, например, здесь.
Когда писал на Qt, использовал функцию qFuzzyCompare, которая определена вот так:
static inline bool qFuzzyCompare(double p1, double p2)
{
return (qAbs(p1 - p2) * 1000000000000. <= qMin(qAbs(p1), qAbs(p2)));
}
static inline bool qFuzzyCompare(float p1, float p2)
{
return (qAbs(p1 - p2) * 100000.f <= qMin(qAbs(p1), qAbs(p2)));
}
А с некоторых пор, если возможно, стараюсь избегать сравнения чисел с плавающей точкой на равенство.
это какая-то дичь извините написана. Нужно сравнивать умножая эпсилон на магнитуду чисел
Я думаю, что вы говорите о немного разных вещах.
Вы говорите о том, что IEEE 754 существует, а ваш собеседник, что его модель настолько плохая, что её и за модель-то считать не стоит.
Ну то есть IEEE 754 в случае переполнения портит вашу бизнес-логику (если нет прерываний, а их почти всегда нет) и вы можете вообще об этом не узнать и вместо ошибки получить какие-то неверные данные на выходе (а NAN вообще в промежуточной переменной с которой сравнились и забыли).
Делить на ноль всё равно нельзя. Все эти пределы и правила Лопиталя сводятся к тому, чтобы путём хитрых преобразований выкинуть это самое деление из вычислений.
Проблема деления на ноль - фундаментальна: в момент деления на ноль разрывается связь в логической цепочке вычислений, и можно получить вообще любой результат. На эту тему полным полно простейших математических фокусов типа "докажем, что 2*2 = 5"
Я для себя пришел к выводу, что goto очень полезен в программирование микроконтроллеров. Когда у тебя какой-нибудь микроконтроллер с флеш памятью под программу меньше 16 Кб, то при помощи goto можно написать более лаконичный и оптимизированный код. А в остальном, я тоже дискриминатор ни в чем неповинного goto. Мне, почему-то, не хочется его встречать в чужом коде, который я читаю.
Я работал в одной организации и был там один проект на микроконтроллере. Был поручен дяденьке который всю жизнь проработал в разных НИИ и не занимался коммерческим программированием. Вначале всё было хорошо. Через пару месяцев образовались огромные ватманы с чертежами блок-схем алгоритмов, начальство котороыми было восхищено и нарисованные алгоритмы начались воплощаться в программы.
В общем, в итоге, ещё через пару месяцев была написана какая-то программа, которую невозможно было отладить. Сказать, что программа была страшна -- ничего не сказать. Там алгоритмы изоморфно переносились в текст. Один лист с алгоритмом -- одна функция. И количество goto примерно соответствующее количество ромбиков со стрелочками в блок-схеме. В принципе можно было сличить блок-схему с кодом и найти сходство. Ещё, поскольку микроконтроллер "на котором нельзя динамически выделять память", эти алгоритмы изобиловали такими ужасами, что где-то в массиве A[12] в один момент времени хранится что-то одно, а в другой -- что-то другое. И главное не перепутать...
Судьба такой программы наверное понятна: была выкрашена и выброшена. После чего было начато программирование "в классическом стиле", когда без блок-схем просто пишется программа, обычным образом, с функциями, операторами и без массы goto, был принесён динамический аллокатор памяти, всё как обычно. Месяца через три была уже рабочая демка, которая скоро стала продуктом. А вот этот ужас с goto никогда продуктом не стал бы. Его постоянно приходилось бы "поддерживать" (чтоб не упал) и невозможно было бы продавать.
Какая-то немного котоламповая история, извините. Похоже, что в организации работали в основном круглые дураки (хотя скорее квадратные - отсыл к военным пенсионерам в менеджменте), либо это были первые 5 лет ее существования.
без блок-схем просто пишется программа
Которую потом никто не сможет поддерживать без блок-схем, UML-диаграмм и т.д. Но организации скорее всего уже наплевать)))
И, само собой, вся эта история не про вред goto, а про то, что программировать надо релевантно, а не как привык на прошлом месте работы. Ну или место работы выбирать релевантно.
Вы не путайте диаграммы с блок-схемами, первые дают взглянуть на систему под другом углом или менее детально, вторые — напротив, заставляют расписывать всё то, что обычно от программиста скрывают компилятор и стандартная библиотека. Да, наверное, если вторые готовить правильно, их тоже можно использовать для чего-нибудь полезного. К сожалению, те, кто считает что именно блок-схема является основным результатом работы программиста, "готовить" эти блок-схемы не умеют совершенно.
Не так давно пришлось мне читать дипломную работу, посвящённую созданию конвертора программ от одного станка с ЧПУ к другому. Сам "алгоритм" преобразования там заключался в 12 заменах подстрок. Угадайте, что было изображено на блок-схеме?
Там был изображён алгоритм поиска и замены подстроки. Очевидно, что именно поиск и замена подстроки — самое важное в конвертере программ для ЧПУ...
Это всего лишь вопрос к тому, что изображать на блок-схеме. Фраза "блок-схема алгоритма" дает автору достаточно свободы для определения того, что он считает алгоритмом, и на каком уровне разукрупнения хочет остановиться.
Мой коммент, как вы заметили, был не в ключе "блок-схемы vs диаграммы - кто победит?", а в ключе "да, конечно, сразу писать код без проектирования - это зе бест практисес". Я причем этот подход не критикую, сам так делаю порой, но тем не менее открыто заявляю всем (и себе), что непризнание программных макетов таковыми - одна из главнейших драм отрасли.
А что стало с дяденькой? Тоже выбросили, или нашлось применение?
Пример очень слабый если честно и похож на "синдром утёнка". Если первый пример goto был от плохого программиста, значит.... если goto => неграмотные спецы, массивы вместо типизированных данные и т.д. и т.п.
А то, что первый же пример (с освобождением ресурсов) - типичный пример из Linux Kernel, где есть goto, а память шарится через union с флагом <=> тип-суммам как-то забывается.
ПС
Ну и да в описанном примере вопрос к менеджменту.
Если 3 месяца на разработку => 2 недели на тулчейн и стенд; 2 недели на дизайн; дальше прогать.
Ну и значит через месяц менеджмент должен был спросить:
- вы код писать уже начали?
- MVP когда
ПС2
Ну и да в похожем примере (если верить описанию) я бы сам начал с дизайна системы, т.к. в похожих случаях (общение драйвера с железкой) реализация API железки очень часто хорошо ложится на конечный автомат с неполной схемой переходов, которую проще сначала описать, потом прогать, чем хомяк-хомяк и в продакшн.
goto ещё крайне полезен в однопроходных компиляторах, где если ты его не используешь - получаешь неподдерживаемую лапшичку, или весьма прямой, конкретный, разбирабельный код если всё таки дёргаешь готушки.
Интересно. А можно пример? Именно компиляторах,не ассемблерах? У меня слово "однопроходный" ассоциируется только с ассемблером. Но в ассемблере же порядок инструкций непосредственно задан.
Однопроходные алгоритмы хорошо ложатся на генераторы и прочие сопрограммы. goto тут нужен только если их в языке нет.
А зачем писать однопроходный компилятор (вы точно компилятор, например с парсером или ассемблером не спутали) в 2023 году?
В своих программах для МК на С использую goto когда это полезно для того что бы сделать более оптимальный по размеру и производительности код. Но я пришел к программированию на С из программирования МК на ASM, поэтому для меня не стояло этой дилеммы. И я не понимал тех кто категорично настаивал на запрете goto .
Это называется -- преждевременная оптимизация. Только проблема в том, что код для современного процессора компилятор оптимизирует, как правило, заметно лучше человека. Потому, что нужно учитывать что инструкции исполняются параллельно, что каждая инструкцию заканчивает исполнение и даёт результат за разное число тактов, и инструкции нужно разложить так, чтоб результат одной инструкции мог использоваться не раньше чем она закончит работу (иначе процессор будет бесполезно жрать), и поэтому можно спекулятивно что-то посчитать, что потребуется через несколько инструкций... Смысла в "микрооптимизациях" никакого, один вред.
Хвостовая рекурсия тривиально оптимизируется компилятором. Пример: https://godbolt.org/z/656Enfb99. Компилятор вообще умеет массу оптимизаций типично много большую, чем сходу придёт в голову программиста. Вот сходу оптимизировать рекурсию в цикл для чисел Фиббоначи -- не может, хотя есть известное решение заключающееся в добавлении дополнительного аргумента функции. Но здесь вся соль отнюдь не в goto, можно просто тело функции поместить в while(1) {} и всё.
Можно руками сделать happy path с минимумом branch (хотя во вложенном branch prediction - сужу по тестам год назад, в последние 6 лет большой прогресс, то что вызывало задержки на архитектурах 5-летней давности предсказывается на архитектурах годовой давности).
Но тут вопрос в том, что не зная прям досконально лучше не лезть.
Улучшить можно, но если не разбираешься - ухудшить можно ещё сильнее, не говоря уже о поддерживаемости кода.
Это ОЧЕНЬ сложный вопрос (если что peephole правила я руками для одного из компиляторов писал).
Если человек понимает что делает - может сделать немного или даже прилично лучше(*) если не понимет - то сильно хуже, как по уровню производительности так и по уровню поддерживаемости кода.
*) тут надо отметить, что по ощущениям вложенный branch prediction за последние лет 6, как я не в компиляторах в x86 хорошо улучшился.
Однажды я попал в ситуацию "сначала предполагались такие задачи, а потом их расширили, но плата уже готова и нужно работать с тем, что есть".
Нужно было 120 раз в секунду связываться с пятью подчиненными устройствами (RS-422, естественно), передавать им данные, принимать данные от них, затем всё это передавать в сигнальный процессор и принимать от него новые данные для нового цикла обмена. И ещё связываться с ПК и реагировать на его команды. Я прикинул быстродействие и приуныл, т.к. получалось очень впритык, единственное, что удалось сделать для улучшения ситуации - заменить версию 8МГц на 16Мгц.
В итоге программа представляла собой одну длинную линейную функцию почти без вызовов других функций (прологи и эпилоги функций на ATmega часто получаются очень длинными), и оператор goto позволил хорошо структурировать это. Естественно, никаких прерываний, только поллинг флагов и чёткий тайминг по микросекундам. Если подчиненный МК не успел ответить за свою одну микросекунду, то не успел, идём дальше. У подчинённых МК программа была примерно попроще, но в том же стиле. Там требовалось вовремя среагировать на то, что во время нашей передачи мастер не дослушал и начал передачу другому МК, значит нужно выключить передатчик.
Так что goto очень даже полезная штука, если применять её по делу. И в данном случае без "предварительной оптимизации" было никак.
Ещё есть __attribute__((__cleanup__)).
Ещё вариант - оформить код в виде автомата, чтобы избавиться от goto:
state = INIT_0;
while (state != DONE) {
switch (state) {
case INIT_0:
state = do_init_0() ? INIT_1 : CLEANUP_0;
break;
case INIT_1:
state = do_init_1() ? DONE : CLEANUP_1;
break;
case CLEANUP_0:
// blah-blah
state = DONE;
break;
case CLEANUP_1:
// blah-blah
state = CLEANUP_0;
break;
}
}Если у человека "талант" в ковычках, то и без goto он может превратить код в нечитаемое что-то, например не использовать нигде name conventions для именнования переменных, обьектов, функций или классов. Если-же у человека настоящий талант, то и с goto он приготовит настоящий шедевр.
Просто надо осознать, по статистике кого больше. Это как с мусором в жизни - повсеместно запрещено кидать мусор где попал, но мусора валом везде. А если-бы не запрещали, а надеялись на личную совесть каждого? Было-бы мусора меньше? Мне кажется- нет.
Мне кажется, пример из ядра Linux логично смотрелся бы в таком виде:
static int mmp2_audio_clk_probe(struct platform_device *pdev)
{
// ...
pm_runtime_enable(&pdev->dev);
ret = pm_clk_create(&pdev->dev);
if (!ret) {
ret = pm_clk_add(&pdev->dev, "audio");
if (!ret) {
ret = register_clocks(priv, &pdev->dev);
if (!ret) {
return 0;
}
}
pm_clk_destroy(&pdev->dev);
}
pm_runtime_disable(&pdev->dev);
return ret; // в оригинале явно возвращался 0
}И кода меньше, и дублирования нет, и меньше вероятность допустить ошибку. Или я где-то ошибся?
В стате про это есть - это Arrow Anti Pattern. Не знаю как в ядре. Но у нас Нередко в ci используются статические анализаторы, которые будут ругаться на высокую вложенность блоков кода.
static int mmp2_audio_clk_probe(struct platform_device *pdev)
{
// ...
pm_runtime_enable(&pdev->dev);
ret = pm_clk_create(&pdev->dev);
if (!ret) {
do {
ret = pm_clk_add(&pdev->dev, "audio");
if (ret) break;
ret = register_clocks(priv, &pdev->dev);
if (ret) break;
...
return 0;
} while(0);
pm_clk_destroy(&pdev->dev);
}
pm_runtime_disable(&pdev->dev);
return ret;
}Можно использовать do { if (error) break... } while(0); для выхода в случае множественных проверок на ошибку.
Те, кто решили, что Arrow Anti Pattern — это антипаттерн, приводят такой пример кода (по той самой ссылке из статьи):
function isCorrect($param1, $param2, $param3)
{
if ($param1 !== $param2) {
if ($param1 === ($param3 * 2)) {
if ($param2 === ($param3 / 3)) {
return true;
} else {
return false;
}
} else {
return false;
}
} else {
return false;
}
return false;
}вместо очевидного такого:
function isCorrect($param1, $param2, $param3)
{
if ($param1 !== $param2) {
if ($param1 === ($param3 * 2)) {
if ($param2 === ($param3 / 3)) {
return true;
}
}
}
return false;
}И делают при этом невинный вид.
Они специально пишут не оптимальный код, выдавая свой вариант за лучший из возможных, чтобы попытаться на этом основании объявить Arrow Anti Pattern антипаттерном.
Нет, это — это именно паттерн, причём, зачастую, он лучше аналогичного с множеством goto и множеством меток, что mobi выше убедительно и продемонстрировал.
Если статические анализаторы "заряжены" неверными посылками, логично неуместную ругань от них отключить или настроить порог их срабатывания на разумный уровень вложенности, если это возможно.
А это да, я же просто отвечал на вопрос mobi, почему в статье отвергается вариант с вложенными условиями.
Статанализаторы обычно настраиваются на какую-то разумную вложенность (которая в примере mobi вполне допустима и даже наверно с запасом в 80 символов помещается). А так-то я как раз не согласен с тем как в статье это объявляется злом которое хуже goto. Также как не согласен, что разбиение на более мелкие функции тоже хуже goto (причем еще и дан специально кривой пример чтобы это продемонстрировать). Обычно это наоборот делает код более читаемым, а оверхеда не дает тк мелкие функции заинлайнятся
в guard стиле тоже симпатично:
function isCorrect($param1, $param2, $param3)
{
if ($param1 === $param2) {
return false;
}
if ($param1 !== ($param3 * 2)) {
return false;
}
if ($param2 !== ($param3 / 3)) {
return false;
}
return true;
}Симпатично, но copy-paste'а в виде повторяющегося return false; мельтешит, дополнительные пустые строки между if'ами раздувают код, и пропадает возможность структурировано освободить ресурсы в случае неудачи.
В том примере по ссылке, мало того, что приведён неэффективный пример, так ещё и не показано преимущество структуры Arrow в смысле структурированного освобождения ресурсов в случае неудачи.
А так?
return ($param1 !== $param2) && ($param1 === ($param3 * 2)) && ($param2 === ($param3 / 3)
Да, конечно.
Но подразумевалось, что там должно быть ещё и структурированное освобождение ресурсов.
Они там специально жульничают, сильно захламив конструкцию и не использовав её преимущество.
Фактически, они использовали её не по назначению, чтобы создать иллюзию, что паттерн — плохой.
А плохой, как раз, не паттерн.
Я уже писал об этом:
В том примере по ссылке, мало того, что приведён неэффективный пример, так ещё и не показано преимущество структуры Arrow в смысле структурированного освобождения ресурсов в случае неудачи.
Без необходимости освобождения ресурсов, естественно, этот код вырождается в логическое выражение.
Если уж брать читабельностью и краткостью, то оптимальный вариант:
return $param1 !== $param2
&& $param1 === $param3 * 2
&& $param2 === $param3 / 3Если не нужно никакого логгирования, то наиболее лаконично, иначе варианты с guard самый оптимальный, ИМХО.
В детстве писал на бейсике, и какое-то время вообще не знал о наличии call, все делал через goto и не чувствовал никаких проблем.
Потом узнал про функции, понял их преимущество. Но при этом четко понимаю что goto - нормальный, полезный оператор в отдельных языках. Да, низкоуровневых, но там где именно ты контролируешь местоположение и кода и данных.
Опять таки, под капотом весь ваш код компилируется во множество goto.
А в бейсике, когда узнали про gosub, сильно страдали от отсутствия локальных переменных? Или вы не узнали, просто язык сменили?
вообще не страдал, и сейчас не страдаю =)
Я четко понимаю, где я бы мог использовать goto в современных языках программирования, но выгоду это принесет минимальную. Ибо удобный для чтения код - важнее в командной работе, чем мелкая оптимизация.
А высокая производительность обычно требуется в очень узком месте, которое можно написать не соблюдая human-friendly стиль, или вообще интегрировать низкоуровневую часть.
В общем я не использую goto не потому, что это плохо, а потому что в подавляющем большинстве случаев, это не нужно. Но если это в конкретном случае нужно - я просто беру и юзаю, без всяких эстетических мучений
Я именно про бейсик спрашивал – где был жесткач, вызвать подпрограмму можно, но переменные в ней те же, что в основной проге. Особенно доставляет при использовании рекурсии (но рекурсивная процедура заливки замкнутой области всё же получалась за счёт трюка "поменяем переменную перед вызовом, восстановим после")
Или вас зацепило ещё какими-то языками без локальных переменных?
ассемблер и бейсик они оба без локальных переменных
в баше есть, но мало востребованы ибо нет смысла писать сложное на баш
В ассемблере был push/pop, так что он не считается :-)
ассемблер и бейсик они оба без локальных переменных
В асме есть локальные переменные, по крайней мере в х86.
local param0:dword
mov param0, 0666h
Конечно можно кодить максимально низко уровнево, но это не правильно. А в старых бейсиках с нумерацией строк, там нет локальных переменных. Но в более современных версиях, типа qbasic, локальные переменные есть и ещё функции и прочее.
Самое интересное, в школьном учебнике математики на полном серьёзе доказывается равенство 0.4(9) = 0.5, что для банковского округления совершенно неверно
В компьютерах не может быть 0.4(9). Нет таких типов
А было бы полезным, по крайней мере, в качестве теоретического построения, чтобы новоиспечённые айтишники не смотрели, как баран на новые ворота, столкнувшись с последствиями матокругления в сфере финансов
0,5 округляется до единицы, 0,4(9) до нуля
0,499...9 с любым конечным количеством девяток округляется до нуля. 0,4(9) - до единицы, потому что его корректное представление при конечном числе значащих цифр - 0,5.
тут некая натяжка, причём двойная, округление 0,5 в большую сторону само по себе - не очевидно
Округление 0,5 в большую сторону - это то, что вы отстаиваете всю ветку, если я правильно вижу. Какая вторая натяжка?
Про округление 0.5 к единице можно прочитать в том же учебнике математики, подается как некий консенсус-договорённость
И это действительно так. Просто договоренность о том, как уменьшить количество знаков после запятой.
В тех языках, где есть типы данных с фиксированной точкой (как правило, это языки для различного рода коммерческих расчетов - там объявление переменной содержит общее число знаков и число знаков после запятой), есть два типа присвоения для случаев когда значение переменной с большим количеством знаков после запятой присваивается переменной с меньшим количеством знаков - присвоение с отбрасыванием "лишних" знаков и присвоение с округлением. В первом случае результат для 0.49 будет 0.4, во втором - 0.5.
Какой тип присвоения когда использовать уже определяется бизнес-логикой.
Из того с чем сталкивался (или слышал) - SQL (типы NUMERIC(n, p) и DECIMAL(n, p)), COBOL, RPG (IBM'овский язык, замена коболу - типы zoned(n: p) и packed(n: p)). Также IBM в С и С++ для middlevare платформы IBM i добавила расширение в виде типов decimal(n, p) и _decimalT<n, p>
Не... Это совершенно другое.
Типы с фиксированной точкой хранятся в памяти совершенно иначе, чем типы с плавающей точкой.
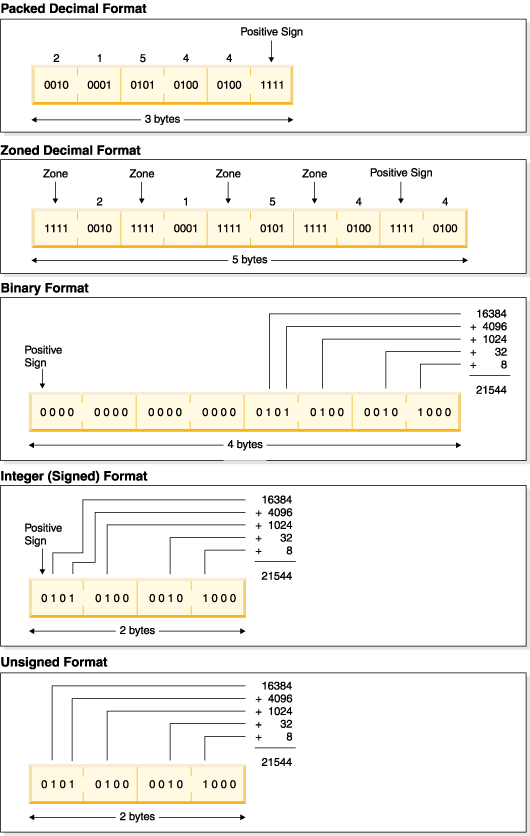
Т.е. тут все знаки числа хранятся в явном виде.
И арифметика с ними совершенно иная. И рекуррентное соотношение Мюллера для таких типов показывает существенно более высокую устойчивость, нежели для типов с плавающей точкой.
Присвоение:
dcl-s p1 packed(6: 3) inz(2.235); // переменная с фиксированной точкой
// всего 6 знаков, 3 после запятой
// проинициализирована значением 2.235
dcl-s p2 packed(5: 2); // переменная с фиксированной точкой
// всего 5 знаков, 2 после запятой
p2 = p1; // обычное присвоение
// последний символ после запятой (5) откидывается
// p2 = 2.23
eval(h) p2 = p1; // присвоение с округлением
// последний символ откидывается
// предпоследний округляется
// p2 = 2.24
p2 = 2 / 3; // без округления
// p2 = 0.66
eval(h) p2 = 2 / 3; // с округлением
// p2 = 0.67такая вот арифметика.
eval в данном случае - модификатор обозначающий некое "особое" присвоение. Для чисел с фиксированной точкой eval(h) - присвоение с округлением. Для строк возможен evalr - "присвоение справа". Для структур - eval-corr - копирование полей, имеющих одинаковые имена (формат структур при этом может быть разным, переносятся только поля с совпадающими именами).
Что-то вы всё в кучу намешали: фиксированная точка, двоично-десятичный код и десятичное основание — это всё независимые вещи, которые могут использоваться как совместно, так и раздельно.
И рекуррентному соотношению Мюллера пофигу на формат хранения, оно одинаково неустойчиво на любых форматах. Имеет значение лишь логарифм единицы младшего разряда.
ChatGPT мне отлично на эту тему высказался, я, говорит, для доказательства равнства 0,(9) = 1 буду использовать трюк) на предложение сделать это без трюка, перевернул с ног на голову, предположил, что 0,0(1) = 0 и тоже доказал)
Ну вообще-то, если на то пошло, это равенство невозможно доказать, оно в стандартном анализе принимается как аксиома. А в нестандартном – не принимается, и это равенство считается неверным.
Это просто свойство, которым мы можем наделить множество R. Ни из чего не следующее.
Если это разные числа, то чему же равна их разница?
Бесконечно малой. Которая в нестандартном анализе рассматривается как самостоятельное число.
Впервые про такое слышу :)
Это самостоятельное число записуемо в виде (конечной или бесконечной) десятичной дроби?
Нет, конечно. Его вообще вычислить нельзя.
Там идея в том, что каждое вещественное число окружено облаком бесконечно мало от него отличающихся. Очень мутная тема.
Там каждое вещественное число окружено облаком невещественных?
И вдобавок вещественные числа там незамкнуты по сложению, что 1-0.(9) даёт невещественный результат??
Нет, они все вещественные, только не все можно построить конструктивно.
В школе, и даже на матмехе, вещественное число - это, по определению, бесконечная дробь.
А там что такое вещественное число?
Это конструктивное определение вещественного числа, оно в данном случае неприменимо.
Но можно же смотреть на вещи и аксиоматически, что вещественное число - это элемент множества R с заданными на нём определёнными операциями (т.е. поля определённого вида). И тогда оказывается, что никакие выводимые из аксиом свойства вещественных чисел не изменяются от того, примем мы существование актуальных бесконечно малых величин или нет.
Бесконечно малой. Которая в нестандартном анализе рассматривается как самостоятельное число.
То есть существует такое число a, что 0,(9) + a = 1.
И особенность этого числа a такая, что оно больше нуля, но меньше любого другого числа (по определению бесконечно малой).
Ну тогда берём b = a / 2 и получаем число ещё меньше. Противоречие, да?
То есть уравнение x * a = x имеет некоторое решение, и это решение не ноль?
О том, куда может завести дорога математических приключений, может поведать, например, это видео.
«Школьные» математические операции не определены для бесконечности. «Школьная» бесконечность — это просто обозначение расходимости и потому выражение a*∞ просто не имеет смысла.
А вот «арифметика бесконечно малых/больших» — она больше похожа на комплексные числа, где у вас вместо символа мнимой единицы символ бесконечности (или бесконечно малого). Но естественно, со своими правилами арифметики.
Вот только является ли 0.(9) нестандартным числом?
Трансфинитное число подставьте на место x.
Вам исчисление первого порядка, собственно, никто не обещал даже в стандартном анализе.
Да какой же другой? Мы об актуальных бесконечностях говорим. Бесконечно больших или бесконечно малых. Которые в стандартном анализе заменяются потенциальными бесконечностями в предельном переходе.
Потом, какая вообще разница, из другой оперы или нет. Важно то, что можно так интерпретировать определение вещественного числа, чтобы ваша теорема не выполнялась.
Неправда (если про нестандартный анализ). Вы получите другое число, но тоже бесконечно малое (их бесконечно много, как и бесконечно больших).
Отнюдь. Бесконечно малое чем-то похоже на «бесконечность наоборот», в частности при умножении/делении на конечное число вы получаете то же самое бесконечно малое (возможно, с другим знаком)
Э-э-э, ну уж нет. Если определять бесконечно малые так как сделали вы — вы не сможете найти производную функции как частное двух бесконечно малых, и зачем тогда это всё?
И особенность этого числа a такая, что оно больше нуля, но меньше любого другого числа (по определению бесконечно малой).
Нет, бесконечно малые числа в нестандартном анализе меньше любого положительного стандартного числа. Их самих бесконечно много и b просто ещё одно из них.
(Вот только с a проблема; в знакомых мне системах нестандартного анализа 0,(9) = 1 никуда не девается и a=0. Но если возьмёте любое положительное бесконечно малое a то да, a/2 другое бесконечно малое меньше него).
Окей, заходим с другой стороны.
Считаете ли вы записи 1/3 и 0,(3) эквивалентными?
В нестандартном анализе? Да. Там вообще все факты о пределах стандартных последовательностей сохраняются.
При этом в последовательностях 0,9, 0,99, ... и 0,3, 0,33, ... будут члены с бесконечно большими номерами, которые будут нестандартными числами, бесконечно близкими к 1 и к 1/3 соответственно. Но последнего среди них нет, за каждым следует ещё более близкое к пределу.
А причем тут последовательности?
1/3 * 3=1
0.(3)*3=0.(9)
Эквивалентность при умножении на одинаковое число сохраняется, значит запись 1 эквивалентна 0.(9) Никаких бесконечно малых между ними
А причем тут последовательности?
При том, что по определению 0.(9) это предел последовательности 0,9, 0,99, ...? Или вы какое-то другое определение используете?
запись 1 эквивалентна 0.(9) Никаких бесконечно малых между ними
Я ровно это и написал выше:
в знакомых мне системах нестандартного анализа 0,(9) = 1 никуда не девается и a=0.
Эта ветка началась с комментария, в котором ошибочно утверждалось, что это не так https://habr.com/ru/post/720486/comments/#comment_25297768.
- бьем прямую на отрезки, ставим точку, записываем последовательность адресов отрезков. и по определению запись 0.(9) обозначает вот эту точку на числовой прямой.
- Извините, перепутал ники.
Мне кажется такое определение куда менее удобным. Тем более:
Если прочитать буквально, 0.(9) у вас получается произвольная точка. Нужно расписать подробнее, как именно прямая разбивается (отрезки произвольные? Одинаковой длины? Уменьшающейся?), как точка на втором связана с отрезками, выбранными на первом шаге и т.д.
"записываем последовательность" странно смотрится рядом с "А причем тут последовательности?".
Поскольку наш контекст -- нестандартный анализ, придётся ещё объяснять, как его числовая прямая отличается от обычной.
Самый 'затык' у него пошёл (>30 секунд раздумий в общей сложности), когда предложил округлить 0,4(9) до ближайшего целого. В первый раз округлил до единицы сославшись при этом на 0,4(9) >= 0,5. Во второй раз, после уточнения, извинился и снова округлил до единицы, сообщив при этом, что 0,4(9) > 0,5. В третий раз выдал результат:
"Извините за недопонимание в предыдущем ответе. 0,4(9) на самом деле меньше, чем 0,5.
Чтобы округлить 0,4(9) до ближайшего целого числа, нужно сначала определить, к какому числу оно ближе. Мы знаем, что 0,4(9) меньше чем 0,5, поэтому мы должны округлить до 0.
Таким образом, при округлении 0,4(9) до ближайшего целого мы получим 0."
Полагаю, станданртным он стал во времена Эйлера, когда математика, как наука, оторвалась от чисто прикладных задач расчётов и банковского дела. Ну и безвестные арабы ещё постаралсь, свергнувшие с 'пьедестала' римскую систему счёта)
Оно следует из геометрической модели построения бесконечной десятичной записи.
Мы бьем всю числовую прямую на полуоткрытые иерархичные отрезки (по 10 штук) и на каждом шаге записываем номер отрезка. Для точки 1 будет запись (0)1.(0) для открытых с одной стороны или (0).(9) для открытых с другой стороны.
Так как разбиения с правым и левым открытым концом в целом равнозначны, то мы не можем сказать "всегда использовать вот такое разбиение". В итоге мы говорим "вот такие пары записей для чисел эквивалентны".
(если можно не буду в этом редакторе расписывать какие "такие")
Вы никогда не докажете, что ваши отрезки покрывают всю прямую (иными словами, что вообще можно выколоть одну точку), не используя то свойство, которое и собрались доказывать.
Почитайте про нестандартный анализ.
Нет, оно спокойно доказывается. Пусть это разные числа, и пусть для определённости 1 > 0.(9), и пусть 1 — 0.(9) = ε (ε > 0), и далее по тексту.
Что далее по тексту-то? Далее по тексту вы его пополам будете делить, рассчитывая получить другое число? А этого никто не обещал для нуля и бесконечно малых.
Любое высказывание про вещественные числа (или, более общо, элементы теории) верно и для нестандартных чисел (или, более общо, расширений модели). Оно там просто по построению модели более высокой мощности так получается.
"Любое вещественное число стандартно".
Для нуля — нет (но ε > 0). Для бесконечно малых — обещал.
Из каких аксиом определения поля R это следует?
Запишите это языком теории вещественных чисел (вернее, real closed fields), тогда продолжим.
А вы запишите этим языком свой предельный переход.
Я прекрасно понимаю, что записать это в виде простого предиката невозможно. Но так же невозможно записать и тот предельный переход, о котором вы говорите (а именно, предел последовательности десятичных дробей, записываемый для краткости как 0.(9)).
Предельный переход вообще не является математической операцией в строгом, формально определённом смысле (каковой, например, является редукция в лямбда-исчислении). Это просто запись некоторого нашего интуитивного способа думать о предмете. Как только видим слово lim, то никакой синтаксически предопределённой интерпретации за ним не стоит.
не является математической операцией
Что вы понимаете под операцией - это не функция? Возьмем множество действительных возрастающих последовательностей на расширенной прямой. Для каждой существует предел на расширенной прямой т.е. существует функция которая каждой последовательности сопоставляет ее предел. Все формально.
Ну напишите тогда мне эту функцию. В том-то и дело, что функцию lim невозможно определить формально, аксиоматически. Это просто некоторые наши рассуждения.
Функция уже написанна - функция это тройка: два множества и функциональный график на их произведении. Все элементы тройки уже приведены выше вполне формально. Что из трех непонятно? С помощью понятия предела я дал вам один пример корректного определения функции. Можно еще, но вы, верятно, говорите о чем-то другом, к тому-же довольно туманно
функцию lim невозможно определить формально
Что это такое "функцию lim"? Вы выдумали что-то свое или прочитали где-нибудь этот термин?
В приведенном мной примере для каждой возрастающей последовательности lim именно формально определенный и существующий, в названных условиях, элемент обобщенной прямой. В общем случае предел это элемент топологического пространства с определенным свойством. Иметь предел, свойство отображения. Все именно формально определено. Определяется существование объекта и не подразумевается алгоритма нахождения/вычисления.
p.s. я не могу отвечать раньше, чем через час.
lim – это гипотетическая функция высшего порядка, которая имеет в качестве аргумента некоторую функцию и значение её аргумента, а на выходе выдаёт значение, к которому стремится функция в данной точке:
y ← lim (f(x), x₀)
Вы как непреложный факт постулируете, что такая функция существует, хотя на самом деле определены только отдельные тройки из двух аргументов и значения, и в каждом случае значение определяется разными рассуждениями. Знание о том, как вычислить предел, например, частного многочленов, ничем не поможет вам найти предел какой-нибудь другой функции.
Если бы предел был определён формально, мы бы могли просто синтаксическими преобразованиями определения функции получать её предел. А оно не так, тут ум нужен.
Возвращаясь к нашей теме, вы по сути говорите: "я утверждаю, что, записывая после "0," неограниченное число девяток, я бесконечно приближусь к значению 1 ..." (это верно и можно легко доказать), "... а такое бесконечное приближение как раз и означает значение предела, строго равное 1" (а вот это просто результат допущения, принятого в матанализе – о том, что бесконечно близкие точки совпадают). Так вы можете волюнтаристски назначить для функции предел, но не вывести его в строгом смысле, как результат формальных преобразований из аксиом алгебры.
lim – это гипотетическая функция высшего порядка, которая имеет в качестве аргумента некоторую функцию и значение её аргумента
В данном случае не функцию и аргумент, а возрастающую последовательность (то бишь, возрастающую функцию из натуральных чисел в вещественные). Впрочем, остальных рассуждений это не отменяет.
Так, стоп: получается, что для вас
функция высшего порядка
это понятие из программирования (https://ru.wikipedia.org/wiki/Функция_высшего_порядка)- правильно?
Не обязательно из программирования. В математике это используется, например, в лямбда-исчислении.
Ну, так, в лямбда-исчислении основным является то, что в отличии от обычного определения функции в математике там есть огромное добавочное требование "computability" - вычислимость (https://en.wikipedia.org/wiki/Computable_function).
Итак, если мы говорим об основном, общем, понятии функции в математике, то там с моим примером, получается, все в порядке. С помошью предела прекрасно определяется функция. Кстати, как раз, в мат. анализе.
Если же говорить именно о вычислимых функциях, то прежде чем продолжать обсуждение, надо разобраться с употребленным вами словом "гипотетическая". Что означает это слово? Вы можете привести источник где это вы видели так определенную функцию
"lim – это гипотетическая функция высшего порядка"
?
Я говорю о значении самого символа lim, а не о пределах некоторых конкретных функций, которые, разумеется, существуют.
Это вы назвали предел функцией. Я написал, что, если бы такая функция, как lim, гипотетически существовала бы, она имела бы описанные проблемы. Но на самом деле предел - это не функция, ни вычислимая, ни невычислимая. Это просто мнемоническая запись формально не выводимого понятия, или скорее даже рассуждения.
Теперь о вычислимости. Если бы lim из матанализа была функцией, то она по определению была бы вычислима, так как на входе имеет конечную запись условия задачи. Можно было бы просто расписать таблицу, в левом столбце которой будут все возможные математические формулы ограниченной длины, а в правом - их пределы. А бесконечными рассуждениям матанализ не оперирует.
Но в действительности мы не знаем пределов некоторых формул, поэтому построить такую функцию не можем.
Это вы назвали предел функцией
Вы все время не отвечаете на прямые вопросы, так, что постарайтесь ответить ГДЕ я назвал предел функцией?
Это просто мнемоническая запись формально не выводимого понятия
Опять-таки, постарайтесь точно ответить, где вы видели подобное заявление о пределе?
Вы все время не отвечаете на прямые вопросы, так, что постарайтесь ответить ГДЕ я назвал предел функцией?
Вы не только не помните, с чем вы вступили в диалог, но и вам лень отмотать на 9 комментариев вверх?
Что вы понимаете под операцией - это не функция? Возьмем множество действительных возрастающих последовательностей на расширенной прямой. Для каждой существует предел на расширенной прямой т.е. существует функция которая каждой последовательности сопоставляет ее предел. Все формально.
Так вот, нет такой функции, которая сопоставляет каждой последовательности её предел. Точно в том же смысле и по тем же причинам, как нет функции, решающей проблему останова. Её невозможно построить, поскольку это изоморфные задачи (рассмотрим последовательность значений счётчика команд машины, выполняющей определённую программу, ну и т.д.)
...
Опять-таки, постарайтесь точно ответить, где вы видели подобное заявление о пределе?
Что значит – где видел? Я это заявление сделал.
А вам хамство мешает видеть, что у меня приведено определение функции с помошью понятия предела а не определение предела как функции?
Вы спекулирете смешивая общее понятие функции с понятием вычислимой функцией и зачем-то приплетая сюда предел.
А вам хамство мешает видеть, что у меня приведено определение функции с помошью понятия предела а не определение предела как функции?
Тогда зачем вы это пишете? Мы обсуждаем понятие предела само по себе.
Отвечу:
Во-первых, не надо хамить. Во-вторых, нахамил, извиняйся. В третьих, последним вопросом вы признаете, что я не называл предел функцией, а вы прямо клевешете, будто-бы я это сделал. И после того, как вас ткнули носом в свою ложь, вы переводите разговор на то, что обсуждение идет фактически понятия предела.
И, наконец:
Я как раз вмешался потому, что вы делаете кошмарное заявление про предел, будто это
просто мнемоническая запись формально не выводимого понятия
Но, это лично ваше, ошибочное, восприятие. Вы основываете это на том, что "невозможно построить" функцию, прямо скажем функционал или оператор, который по данной функции и данной точке давал-бы значение предела. Тут, во-первых вы должны явно подчеркивать, что речь идет о вычислимой функции, а не функции вообще. Во-вторых, как обычно принято в математике, надо говорить не о решении вообще, а о решении в определенном классе. Довольно просто назвать такой класс функции в котором построить подобный функционал не проблема. Вероятно можно назвать такой класс, где функционал построить нельзя, но, это сперва нужно доказать. А потом это обычная ситуация в математике: где-то решение есть, где-то его нет. Манипулировать этим и обзывать одно из самых формально точно определенных понятий математики - понятие предела - какой-то "мнемонической записью", это я и называю спекуляцией ради красивого словца, хайпом.
Мне кажется, хамить здесь пытаетесь только вы.
В третьих, последним вопросом вы признаете, что я не называл предел функцией, а вы прямо клевешете, будто-бы я это сделал
Вот это вот:
Возьмем множество действительных возрастающих последовательностей на расширенной прямой. Для каждой существует предел на расширенной прямой т.е. существует функция которая каждой последовательности сопоставляет ее предел.
кто написал?
Функция, сопоставляющая каждой последовательности её предел, не существует ни в вычислимом, ни в невычислимом классе. Точно так же как не существует множество всех множеств или функция-оракул, которая по тексту произвольного высказывания определяет его истинность. Это просто языковая игра, не имеющая формального содержания. А суть тут в том, что неверно допущение о возможности найти предел произвольной последовательности, или даже просто установить существование предела произвольной последовательности.
И я даже выше вам приводил пример последовательности, предположение о наличии либо отсутствии предела у которой приводит к противоречию.
одно из самых формально точно определенных понятий математики - понятие предела
Да ни фига оно точно не определено. Определены только различные необходимые условия по типу: если у нас есть функция f и значение y такое, что (blablabla), то y называется пределом f.
прямо скажем функционал или оператор
Если вам хочется называть это функционалом или оператором, я не возражаю. Мне такая терминология представляется менее конструктивной, поскольку порядок функции можно повышать неограниченно, и разных слов не хватит.
И я даже выше вам приводил пример последовательности, предположение о наличии либо отсутствии предела у которой приводит к противоречию.
Где? Что-то я не вижу...
Пятый комментарий вверх от вашего.
На всякий случай, напишу ещё раз.
Пусть последовательность Θn(T) обозначает положение головки машины Тьюринга с лентой T на n-ном шаге. Если мы выведем предел этой последовательности по n, это будет означать, что мы решили проблему останова для T в положительном смысле. Если мы выведем, что предела нет, это будет означать, что мы решили проблему останова для T в отрицательном смысле. То и другое невозможно. Существуют такие значения T, для которых нельзя оценить Θ, не проделав все n шагов. А это и означает отсутствие формализма предела.
Это вы сейчас написали почему пределы некоторых функций невозможно вычислить. Но это не означает что самой функции предела не существует.
Что вы вкладываете в понятие функции, для которой невозможно вычислить её область определения?
Именно это и вкладываю. В чём проблема функции, для которой невозможно вычислить область определения?
Ну функция – это вроде бы как по определению морфизм из множества А в множество B. Нет множества – нет функции.
Невычислимое множество всё ещё существует
В аксиоматической теории множеств не может быть невычислимых множеств. ZFC представима в лямбда-исчислении определённого вида.
"Множество останавливающихся МТ" существует или не существует?
Аксиоматическая теория множеств не знает что такое последовательность, функция, предел, машина Тьюринга и т.п., потому в ней всё и так просто.
Другие разделы математики не такие простые, в частности уже аксиомы вещественных чисел в логике первого порядка не выразимы.
Назвать хама хамом это не хамство, а констатация хамства.
Далее:
Вот это вот:
Возьмем множество действительных возрастающих последовательностей на расширенной прямой. Для каждой существует предел на расширенной прямой т.е. существует функция которая каждой последовательности сопоставляет ее предел.
кто написал?
И где здесь написанно что предел это функция?
И разве непонятно, что в первом предложении специально подчеркнуто множество по отношению к которому и употреблен квантор всеобщности во втором?
Следующий момент:
вы нарочно передергиваете? Вы пишете
Функция, сопоставляющая каждой последовательности...
Разве у меня написанно "каждая"? Сами же приводите цитату в которой у меня написанно "множество действительных возрастающих последовательностей на расширенной прямой".
Сколько вам привести книг по мат. анализу и их известнейших авторов, где это элементарная теорема, что у возрастающих последовательностей на расширенной прямой существует предел? Опять же стараться это поставить на один уровень с множеством всех множеств, есть еще одна спекуляция. Разумеется, если у вас настолько распухло самомнение, что вы отметаете классический мат. анализ, то это прекрасная характеристика ценности всех ваших высказываний и хороший момент где продолжение разговора теряет смысл.
И наконец
определение есть не необходимое условие для самого себя, а эквивалентное.
Я как раз и пишу об изоморфности этих задач. Если бы можно было так расписать пределы, то и проблему останова тоже.
Теперь о вычислимости. Если бы lim из матанализа была функцией, то она по определению была бы вычислима, так как на входе имеет конечную запись условия задачи. Можно было бы просто расписать таблицу, в левом столбце которой будут все возможные математические формулы ограниченной длины, а в правом - их пределы. А бесконечными рассуждениям матанализ не оперирует.
Предел может существовать и при этом быть недоказуем -- это следствие из https://ru.wikipedia.org/wiki/Теоремы_Гёделя_о_неполноте
lim из матанализа -- это отличный пример невычислимой функции. Результат прогона машины Тьюринга -- тоже функция и тоже невычислимая.
Предел может существовать и при этом быть недоказуем — это следствие из теоремы Гёделя о неполнотеДовольно спорно.
Если у нас для пары число-последовательность может быть три варианта:
— эта пара удовлетворяет определению предела
— эта пара неудовлетворяет определенеию предела
— невозможно доказать удовлетворяет или нет
То только в первом случае мы можем говорить о том, что число является пределом последовательности.
Иногда мы можем доказать, что последовательность имеет предел, но не можем установить какой именно — но это другой вопрос.
У всякой последовательности либо есть предел, либо нет предела, верно?
Каким образом это следует из теоремы-то? Какая существует непротиворечивая формальная арифметика, в которой все формулы, кроме наличия или отсутствия предела у определённых последовательностей, являются либо выводимыми, либо опровержимыми?
По вашей же ссылке написано:
Поскольку, вообще говоря, не существует общего метода, позволяющего для любого высказывания за конечное число шагов установить его истинность или истинность его отрицания, закон исключённого третьего не должен применяться в рамках интуиционистского и конструктивного направлений в математике как аксиома.
Ровно об этом я выше и пишу: что утверждение может быть истинным, и при этом недоказуемым.
В вашей же цитате написано:
Поскольку, вообще говоря, не существует общего метода, позволяющего для любого высказывания за конечное число шагов установить его истинность или истинность его отрицания, закон исключённого третьего не должен применяться в рамках интуиционистского и конструктивного направлений в математике как аксиома.
В рамках стандартной математики это всё ещё аксиома. Смиритесь уже с этим.
Предел может существовать и при этом быть недоказуем
Может. Но это не тот случай.
Результат прогона машины Тьюринга – и вправду, (невычислимая) функция, так как он определён на известном множестве лент и шагов, а именно, на любой ленте и любом шаге. С lim такой номер не проходит.
из него делаете вывод, что они равны
На основании чего такой вывод? Тут можно только сделать вывод, что ε можно бесконечно уменьшать.
Раз уж вы считаете только технической сложностью отображение из N в R, то возьмите трансфинитный ординал, который при сложении с самим собой даёт себя, примерно таким же образом отобразите его в расширенное R, посчитайте обратную величину, и вот вам актуальная бесконечно малая, которая при делении пополам не уменьшается.
Ну и где вы такой ординал найдёте-то?
Т.е. в общем случае нет однозначного алгоритма нахождения предела.
Но если так рассуждать — то и нахождение первообразной или любого другого интеграла — не операция.
Имеется ввиду что само нахождение предела — это скорее доказательство теоремы, что некое число связянно с некоторой последовательностью так как это описывает определение предела.
Да. И это требует дополнительного допущения, что бесконечно близкие числа совпадают. Само это допущение ниоткуда не следует.
Нахождение первообразной – не формально определённая операция тоже.
Ну вообще-то, если на то пошло, это равенство невозможно доказать, оно в стандартном анализе принимается как аксиома.
Возможно, конечно, и достаточно просто. Где вы видели изложение анализа, в котором оно было бы аксиомой?
А систем нестандартного анализа много, и по крайней мере в тех, которые мне лучше знакомы, 0,(9) (если его определять как lim_{n->бесконечность} (1-1/10^n)) по-прежнему равно 1 и существование бесконечно малых чисел этому никак не мешает.
В некоторых ЯВУ есть рациональные типы. Там что-то подобное можно получить (при переводе в десятичную систему).
В Ruby, например, есть. Как выше заметили - рациональный тип.
Так верно же. В момент каста в тип с фиксировнным числом знаков после точки произойдет округление по математическим правилам и появится ожидаемое 0.5000
это вот 2.0f*2.0f <> 4.0f, но экспоненциальное представление в банковских приложениях использовать черевато.
2.0f*2.0f <> 4.0f
Интересно, почему? И 2 и 4 представимы во float точно (как и все целые числа до 223, так как именно столько бит в мантиссе), почему результат этого вычисления должен оказаться неточным?
Склероз. Помнил, что вылетал в 3.9999999999999е0, но сейчас проверил на питоне, 4.0 получается.
Например, потому, что про результат вещественных операций в реальных процессорах не гарантируется, что он совпадает с наиболее точным математическим представлением. И он запросто может различаться в младших битах на разных чипах.
Это было бы понятно, если бы число не было бы точно представимо в двоичном представлении. Но и 2 и 4 — точные степени двойки, при перемножении так или иначе множатся мантиссы как обычные целые числа, перемножение целых всегда точно. Откуда конкретно в данном примере могут быть неточности?
Никто не гарантирует, что мантиссы будут умножаться как целые числа. Скорее нет, чем да. Мало ли какие там техники приближённого умножения.
Помнится, на некоторых процессорах вещественное умножение быстрее целочисленного.
Говоря предметно, когда вы будете 4 сдвигать влево, чтобы нормализовать к 2, то почему вы уверены, что в младший разряд запишется 0?
Потому что стандарт IEEE гарантирует получение ближайшей к точному результату двоичной дроби.
А почему вдруг 0 ближе чем 1?
Это только ваши наивные интуитивные представления, что незаписанные разряды равны 0.
Отнюдь, это требование IEEE.
Весь смысл стандарта -- в том, что одинаковые действия над побитно одинаковыми числами приведут к одинаковым результатам на любой системе, соблюдающей этот стандарт.
Вы совершенно неправильно понимаете стандарт IEEE, и на практике результаты вычислений на разных процессорах различаются.
Какое место в стандарте вы интерпретировали таким образом?
Стандарт гарантирует только отсутствие аномалий.
и на практике результаты вычислений на разных процессорах различаются
Пруф или не было
Личный практический опыт, amd vs intel. У нас в фирме после этого покупку amd запретили, чтобы контрольные примеры побитово сходились.
Ну это давно было и редко, конечно, но тем не менее.
Какое место в стандарте вы интерпретировали таким образом?
"Each of the computational operations that return a numeric result specified by this standard shall be performed as if it first produced an intermediate result correct to infinite precision and with unbounded range, and then rounded that intermediate result, if necessary, to fit in the destination’s format"
Ну это давно было и редко, конечно, но тем не менее.
Если у вас нет конкретных примеров, то и обсуждать нечего: доказывать отсутствие заварочного чайника в поясе астероидов я не собираюсь.
Согласен, что в отношении умножения я погорячился, но, тем не менее, стандарт требует соответствия результатов только от:
add, subtract, multiply, divide, extract the square root, find the remainder, round to integer in floating-point format, convert between different floating- point formats, convert between floating-point and integer formats
К вычислению более сложных функций это требование не относится.
доказывать отсутствие заварочного чайника в поясе астероидов я не собираюсь
А вы не доказывайте, а слушайте людей, обогатившихся собственным опытом.
А вот, кстати, один из примеров, в данном случае квадратный корень. Для понятности приведена ассемблерная команда, но gcc, как пишут, генерирует аналогичный код в режиме -Ofast.
Может быть доля в чем-то равная одной трети, например. В юридических документах. И это надо хранить.
Самое интересное, в школьном учебнике математики на полном серьёзе доказывается равенство 0.4(9) = 0.5, что для банковского округления совершенно неверно
Оно, в таком виде, и для банковского округления верно. Хотя бы потому что операции округления в этой записи вообще нет.
Речь, конечно, о 'теореме' 0,(9) = 1, весьма вредная штука, её бы вообще изъять из учебников, либо излагать вместе с понятием о банковском округлении. Просто взяли и 'скушали' ни в чём неповинное число. Используя 0,4(9) отличное от 0,5 возможно построить теоретическую модель без потерь, вызванных правилом округления 0.5 в большую сторону. Кроме того 'проистекающие' из подобного соотношения утверждения вида -0.0(1) = +0.0(1) аналогичны, в моём понимании, стягиванию земных полюсов в одну точку и полной отмене электричества.
Математика — это стройная система, а не набор хаков для финансовых расчётов. "Починить" финансы и уронить всё остальные расчёты — так себе затея.
Проблемы округления нормально описываются и исследуются классической математикой, только не в школе.
В чём будет нарушена стройность и какие расчёты валятся-падают - совершенно непонятно. Казус этот всплывает, при попытке представить показательные дроби в виде десятичной записи с периодом, 1/3 = 0,(3), при этом нет дроби для записи 0,(9)
Правильно. А нет её потому что 0,(3)3 = 1/33 = 1. Вы предлагаете операцию деления сделать необратимой или как?
Так, разметка скушала умножения. Вот так надо читать: 0,(3)*3 = 1/3*3 = 1
Идеальная стройность и красота школьной математики рушится выражением 0,4(9) < 0,5, а 'теорема' о равенстве-эквиваленции 0,(9) и 1 является неким прикрытием и заметанием под ковёр данного факта, как собсенно и запрет на использование безусловного goto, уже в высшей школе, закрывает кучу пр'облемов и неоднозначностей на этапе компиляции, вызванных его применением
Идеальная стройность и красота школьной математики рушится выражением 0,4(9) < 0,5
...для которого до сих пор не видно доказательства.
О том и речь, невозможно заявить чтобы кто-нибудь не потребовал доказательства)
Естественно. Либо доказательство, либо явное утверждение, что это неравенство принимается за аксиому (и дальше смотрим, что из этой аксиомы будет выводиться и насколько удобно с этим будет работать).
Только вот 0,4(9) = 0,5 и ничего не рушится.
а 'теорема' о равенстве-эквиваленции 0,(9) и 1 является неким прикрытием и заметанием под ковёр данного факта
какого факта?
Если применить альтернативное деление столбиком:
1|2
0|---
-|0.4999...
10
8
--
20
18
--
20
18
--
20
18
--
2то получатся удивительные результаты.
1 делится на 2 не нацело, запишем 0 в частное, и 1 будет в остатке.
Ставим десятичную точку в частное, дописываем справа 0 к остатку, получается 10.
Далее, 10 делится на 2 нацело, и получается 5, но в данном случае деление — альтернативное, поэтому запишем в частное 4, а в остатке, соответственно, будет 2.
Дописываем к остатку 0, получается 20, которое тоже делится на 2 нацело, и получается 10, но такой цифры нет, поэтому запишем максимальную цифру, то есть, 9 в частное, и тогда 2 будет в остатке.
Дописываем 0, получается опять 20, поэтому опять записываем 9 в частное, и опять 2 будет в остатке.
Очевидно, что процесс замкнулся и стал бесконечным.
Итак, обычным делением столбиком получается 0.5.
Альтернативным делением столбиком получается 0.4(9).
В школьной математике, скорее всего, такого нет, потому что я сам это придумал.
Теперь доказывать якобы неравенство 0.4(9) != 0.5 стало труднее.
В старославянском языке было некотороеограничение против подобного, знак тилто над буквой, для обозначения числа, т.е. на результат деления 0,(Д) тилто можно было не ставить и дальнейшее действия не производить делимое/делитель = (стоп) без тилта
Причём тут вообще язык? Математика от языка не зависит.
с,(топ), если точнее, ну цифрой 666 вряд ли кого напугать-предупредить можно, словами-цифрами эт сделать несколько 'проще' и диапазон - шире, а так - да
Цифрой 666 лично меня напугать очень легко, т.к. страшно представить себе тех, кто использует систему счисления с настолько большим основанием (если, конечно, считать, что эта цифра соответствует десятичному числу с той же записью). Но все эти эмоциональные реакции в любом случае не имеют отношения к аксиоматике и выводимым из неё следствиям.
тем более, переходим на старорусские букво-цифры и 'лечим' 666-боязнь))
А чем они-то тут помогут? Цифра 725, к примеру, меня напугала бы дословно так же. Да даже цифра 123. С цифрой 1000 чуть-чуть получше (римскую систему записи мы все помним, я надеюсь), другой вопрос - зачем это нужно, если позиционные системы в практических задачах почти всегда удобнее.
китайские иероглифы - помогут, если не знать китайский, берём их, навешиваем тилты и вперёд, математика не для простых смертных
Так тогда это не цифры. Символьные вычисления - это совсем другая задача, да.
Вики в помощь: '
в некоторых языках, например, в церковнославянском, древнегреческом, иврите и др., существует система записи чисел буквами'
В этом случае буквы являются цифрами, и знание/незнание языка на это не влияет. Максимум - может использоваться как мнемоника, если значения цифр согласованы с алфавитным порядком.
'цифра 725, к примеру, меня напугала бы', а в чём особенность 725, если не привязываться к языку? В дореформенной орфографии были правила поминай/не поминай беса, проистекающие как раз из цифрабуквенной связки, ну и в китайском нет строго определённого алфавитного порядка, как в языках, на основное латыни, несколько мне известно
а в чём особенность 725
Цитирую самого себя:
страшно представить себе тех, кто использует систему счисления с настолько большим основанием (если, конечно, считать, что эта цифра соответствует десятичному числу с той же записью).
Так что "особенность" здесь такая же, как и у 724, и у 726.
тогда у меня unicod-фобия, не говоря уже об utf-32
Сочувствую, но при чём тут это? Числа там, конечно, большие, но цифры, насколько мне известно, вполне обычные.
это ж какую голову иметь надо, чтобы представить себе систему счисления с основанием 32К.. таблицу умножения прикинь)
твоя моя не понимай, речь вроде как о системе счисления с основанием 752 и выше..
Тут кажется идет активный троллинг между "позиционная система, сколько цифр, такое и основание" и "историческая система, если число записывается буквой, то эта буква — цифра, но к основанию системы счисления отношения не имеет".
Насколько я понимаю, на Руси была вполне себе десятичная система счисления, однако цифра 900 тоже была
"Значение 900 в древности выражалось «малым юсом» (ѧ), несколько похожим на соответствующую греческую букву «сампи» (Ϡ); позже в этом значении стала применяться буква «ц». " (С) вика
Казус этот связан исключительно с тем, что вы пытаетесь вкладывать смысл в форму записи числа.
Если вы утверждаете, что 0,(9) != 1, то которое равенство неверно?
1 = 9 * 1/9 = 9 * 0.(1) = 0.(9)
Используя 0,4(9) отличное от 0,5 возможно построить теоретическую модель без потерь, вызванных правилом округления 0.5 в большую сторону.
О каких таких "потерях" идёт речь вообще?
А вот в golang, например, кейс с множественной инициализацией и очисткой нативно решается использование defer
Кейс с выходом из внешнего цикла решается break с меткой в том же golang
Кейс с ретраем нарочно не показывает более логичный вариант с циклом for(;;) + continue который вообще мало будет отличаться от исходного варианта но в качестве бонуса получим визуальные границы ретрая в виде {}
Вобщем написано много слов но по сути вывод то вот такой имхо: действительно нельзя обойтись без goto в C, но это диктуется низкой выразительностью языка и отсутствием его развития (кто мешает сделать те же break/continue с метками непонятно). И именно поэтому популярность C для написания несистемных программ такая низкая, особенно после появления golang.
Справедливости ради, не golang единым - примерно в любом языке, где есть деструкторы или обработка исключений (в лице блока finally), goto в кейсе "не забыть очистить ресурсы", особо-то и не нужен.
А вот break/continue с метками был бы полезен, много где.
Механизм деструкторов и finally довольно плохо ложится на сценарий, когда требуется условная очистка ресурсов (не отматывать операции при успешном выполнении цепочки операций).
Если не нужно очищать ресурсы, то по идее надо сохранять объект, который ими управляет, в области видимости (ну, вернуть его там или сохранить куда).
А про finally согласен.
В этом плане становится сложно, например, в C#, ибо даже вылетевший из области видимости объект, вообще говоря не удаляется. И что делать, кроме как явно очищать всякие файлы и сокеты (или возиться с IDisposable, но по сути, тоже, явно) - непонятно.
В С++ — да, следуя идеологии RAII, можно обернуть каждое владение ресурсом в объект, а потом, в случае успешности всей цепочки, используя move semantics, передавать эти объекты наружу в составе другого объекта. Единственный недостаток здесь — хранение контекста, который нужен для освобождения ресурса.
В C# — да, используйте IDisposable. Я нахожу это достаточно удобным.
А где именно эта популярность низкая? По TIOBE вниз идёт как раз Go.
Не хотел отвечать тк холиварно, но ваше утверждение про tiobe неверно: в марте 23 golang впервые вошел в 10-ку на tiobe. Ну и сам индекс tiobe такой себе показатель. Предлагаю в качестве альтернативы, например, посмотреть стату github там есть графики по годам и видно развитие популярности наглядно. Открытые вакансии это тоже подтверждают: если C (не c++), то либо что-то системное, либо embed разработка - полистайте hh
Автор забыл сказать, что goto привносит свой букет проблем: в первую очередь из-за возможности "перепрыгнуть" инициализацию переменных. О чём современные компиляторы могут предупредить, а могут и не предупредить. И почему в C++, в отличии от C, не всякие goto возможны. И это один из мотивов, почему в Linux боятся local scope переменных и по-старинке объявляют все переменные в начале функции (второй мотив, что это позволяет избегать висящих указателей на локальные переменные). Но это в свою очередь тоже ничего хорошего не приносит, т.к. теперь константную переменную присвоить невозможно и ключевое слово const избегается, что ведёт к другим ошибкам.
Приведённые автором примеры "как обойтись без goto" хоть и выглядят страшно, но легко читаемы сверху-вниз, обладают меньшей циклотомической сложностью. В отличии от спагетти-кода с goto;

Вообще критика goto берёт свои корни из фортрана, пример приведён выше. Когда программа записывалась "в столбик" как в ассемблере:оператор-строка, что пошло от перфокарт (где было только 80 колонок и ни одной больше). Толковых операторов вертвления в языке не было, зато были развитые варианты goto (оператор IF). Такие программы было очень трудно воспринимать, очень легко наделать ошибок. Это было очевидной проблемой в ответ на которую возникло так называемое структурное программирование, основная идея которого в отказе от макаронных монстров из goto и в использовании специализированных управляющих конструкций или операторов (if, while, for, switch...) Такой код обладает меньшей сложностью и менее подвержен ошибкам. По ссылке приведён прекрасный обратный пример, как макаронный goto-монстр может быть превращён в читаемый код: https://craftofcoding.wordpress.com/2020/02/12/the-world-of-unstructured-programming-i-e-spaghetti-code/
И следует отметить в Linux не просто "широко используется goto", а реализован определённый паттерн программирования, фактически ручная реализация отсутствующего в языке C оператора defer, подробности по ссылке: https://gustedt.gitlabpages.inria.fr/defer/ В языке C++ для аналогичных целей Александреску предлагалась концепция "Declarative Flow Control", в частности шаблон/функция SCOPE_EXIT. Что в современных условиях может заменяться std::unique_ptr с определённым программистом deleter'ом и лямбда-функцией:
auto on_exit = [&](void *)
{
// Do deferred job.
};
std::unique_ptr<void, decltype(on_exit)> catch_exit {this, on_exit};
Другим полезным использованием goto является выход из вложенных циклов. Его конечно можно реализовать в рамках структурного программирования с использованием дополнительной переменной, но часто объективно, код с goto в данном случае (а не вообще) -- лучше.
Резюмируя: в целом -- goto опасный и плохой инструмент в очумелых ручках. Но иногда он нужен и полезен. Иногда. Точно так же, как и ассемблерные вставки. Иногда. В целом кода с goto следует избегать, особенно неопытным программистам, и стремиться использовать элементы структурного программирования: специализированные операторы и разбивку кода на отдельные функции если необходимо.
К несчастью в языке C отсутствует понятие лямбды, отсутствуют локальные для процедуры функции (как в Паскале), что затрудняет разбивку кода (т.к. функции часто нужен ещё и контекст, который трудно передать через переменные). Ввиду этого пишутся огромные по размеру функции и возникает goto (обработка ошибок, прерывание вложенных циклов). В Clang конечно есть code blocks, но их нет в GCC, а вложенные процедуры в GCC (которых нет в Clang) требуют трамплинов и в современных условиях мало применимы...
Собственно из-за этого и вбивают в голову 'не пользоваться goto'
Что характерно, арифметический IF выкинули из Фортрана 35 лет назад, а борьба с ним живёт до сих пор.
Первый Фортран 1954 года, на самом деле, не очень-то отличался от макроассемблера, там ещё и не такие прибабахи были. Была у машины IBM 704 инструкция арифметического ветвления, её и продублировали в языке. Там ещё какие-то операторы специально для управления магнитным барабаном были, что ли. Но всё это потом почистили потихоньку.
Вот эти рассказы про Фортран - означают, что вопроса опять не поняли, и опять борются с ветряными мельницами образца 1960 года, которые давно как неактуальны. О чем, собственно, и рассказывает статья.
множество точек выхода
А почему это вдруг минусом является? "Ранний возврат" вполне распространенный паттерн
В языках с явным потоком управления, куда относится C, становится важно иметь единственную точку выхода из функции. В C++ можно просто добавить к локальным переменным функции объект и деструктор всё сделает на выходе, в любом случае. В C нужно явно прописывать действия на выходе. Чему ранний выход может помешать, в том смысле, что провоцирует на ошибку (про него просто можно забыть).
Хм, в этом плане наверное справедливо
Собственно это и хотел написать. Статья про то как полезен GOTO в си, при том что в любом современном языке с деструкторами такой проблемы н стоит в принципе, а других преимуществ у него собственно и нет. Разводить софистику что свитч это гоуту, вызов функции это гоуту и вообще всё гоуту — считаю ересью.
Тот 'goto', против которого возражал Дейкстра, это сегодня - 'nonlocal goto' (longjump, setjump и.т.п.). В современном виде эта штука вернулась к нам в виде короутин.
Я извиняюсь, а чем пример оптимизация хвостовых вызовов хорош?
в чём там приемущество в сравнение с обычным циклом?
годболт показывает абсолютно одинаковый выхлоп и читаемость кмк с цыклом лучше чем с goto


Ничем не хорош, о чём и пишет автор статьи. Суеверие.
Точно такой же циклический код вы получите и при простом незамысловатом рекурсивном вызове с одним параметром, так как наивное вычисление факториала – это стилизованная рекурсивная функция, а компилятор умный.
ну он просто пишет что тут есть какая то оптимизация завязанная на goto для старых компиляторов, вот у меня и возник вопрос, а при чём тут goto когда это отлично решается и другими конструкциями и где goto как раз таки не стоит использовать.
Направление мыслей автора в целом верное, но на некоторых примерах его заносит. Например, переход между ветвями case я бы не назвал хорошей практикой.
В настоящее время большую часть кода пишу на языке, где нет goto. Просто нет.
Зато есть сабрутины (subroutines) как в древнем бейсике - именованный блок кода внутри области видимости процедуры (т.е. использующий локальные переменные процедуры и не образующий уровень стека при вызове).
Поначалу казалось "фу, как бейсике...", потом проникся - во-первых, еще один инструмент для структурирования кода, во вторых, удобный инструмент когда один и тот же блок кода нужно или выполнить несколько раз, или обращаться к нему из разных точек процедуры.
Также на них легко реализуется "единая точка выхода":
...
if <некоторое условие>;
exsr srExit;
endif;
...
if <другое условие>;
exsr srExit;
endif;
...
exsr srExit;
return; // просто обозначате конец процедцры
// объявление точки выхода
begsr srExit;
// делаем что нам надо на выходе
return; // а это уже "настоящий" выход
endsr;Хотя там есть и механизм on-exit:
dcl-proc myproc;
dcl-s isAbnormalReturn ind;
...
p = %alloc(100);
price = total_cost / num_orders;
filename = crtTempFile();
return;
on-exit isAbnormalReturn;
dealloc(n) p;
if filename <> blanks;
dltTempFile (filename);
endif;
if isAbnormalReturn;
reportProblem ();
endif;
end-proc;В блок on-exit попадаем всегда или при выполнении оператора return (сколько бы их ни было) или при возникновении исключения (например, при делении на ноль).
При нормальном выходе индикатор isAbnormalReturn будет off, при вылете по ошибке (исключении) - on;
Также можно переопределять возвращаемое значение внутри on-exit
dcl-proc Division ;
dcl-pi *n packed(7:3) ;
Dividend packed(5) const ;
Divisor packed(5) const ;
end-pi ;
dcl-s Result packed(7:3) ;
dcl-s ErrorHappened ind ;
Result = Dividend / Divisor ;
return Result ;
on-exit ErrorHappened ;
if (ErrorHappened) ;
return -1 ;
endif ;
end-proc ;В общем и целом, все эти механизмы вполне позволяют обходиться без goto и при этом писать читаемый и логически структурируемый код.
Почему как в бейсике, а не как в паскале? В классическом бейсике никаких областей видимости и даже локальных переменных не было, а процедура внутри процедуры – это паскаль, довольно удобная штука, но за неё приходится платить: помимо указателя на стекфрейм текущей процедуры – нужен указатель на стекфрейм родительской, чтобы дотянуться до переменных (просто использовать фиксированное смещение от текущего стекфрейма нельзя, т.к. может быть несколько процедур, вызывающих друг друга, или вообще рекурсия).
Потому что речь идет о RPG (это такой специализированный язык для коммерческих расчетов от IBM - 80% кода на их middleware платформе IBM i пишется на нем). Ровесник кобола, но до сих пор развивается.
Так вот ранние версии там имели fixed нотацию

и там не было поддержки процедур, только сабрутины. В этом плане он был ближе всего именно к бейсику. И в той версии goto было
Потом от этого безобразия ушли, сейчас это нормальный процедурный язык.
goto из новой (т.н. "free") нотации убрали, добавили процедуры, но сабрутины остались просто перейдя внутрь процедур.
Слышал, что go to это не очень, старался не использовать. И когда у одного сокурсника увидел лабу, где почти все конструкции for были построены на go to - If - моя жизнь резко поделилась на до и после.. Сейчас, спустя 20 лет я использую все, что доступно: goto, continue, return, break. Так, как хочу. И счастлив. Если ты понимаешь, что и как работает, какая разница какими методами и инструментами достигается цель?
Всё хорошо, но пример со switch странный - там ведь на то и break, чтобы можно было писать один общий блок кода под несколько case сразу. И в этом случае ни goto, ни общая функция не нужны.
Там не общий кусок кода под всеми вариантами. Там каждый вариант начинается со своего куска кода (инициализация некоей (одной и то же) переменной определённым значением), а потом идёт общий кусок для всех веток. Если вы там просто break пропустите, то во всех ветках переменная будет инициализирована одним и тем же значением — последним встретившимся.
Всё хорошо, но пример со switch странный - там ведь на то и break, чтобы можно было писать один общий блок кода под несколько case сразу.
до сих пор не понимаю зачем вообще нужен синтаксически break в каждом case, ведь как только заканчивается блок и начинается cледующий case, то ведь и без break понятно, что выход из switch происходит...если он конечно внутри используется для преждевременного выхода, то тогда ок, согласен.
switch (a) {
case 1:
do_something();
case 2:
do_more();
}при a==1 будут вызыван обе функции.
иногда это действительно удобно, но в целом я понимаю создателей golang, которые посчитали это bad practice, сделав явный fallthrough.
при
a==1будут вызыван обе функции.
в том-то и дело, но свободно-стоящего case-оператора не может существовать в природе, т.е. не может после do_something(); компилятор если честно "не увидеть" case 2:. И то, что это в c-языках так и будет выполнено мне понятно, но считаю - ненужным.
мне кажется, вы просто упускаете контекст появления языка.
во-первых, это было очень давно, когда разработка ПО только зарождалась; во-вторых изначально язык создавался максимально близким к ассемблеру, в том числе с точки зрения простоты компилятора.
если смотреть с такой точки зрения, то многие решения, принятые при создании языка, становятся понятнее.
не его вина, что он стал использоваться буквально везде.
Согласен с вами полностью и да, я понимаю и использую это уже лет 30, но просто говорю, что нелогично был сделать так. Хотя, если подумать, что оплата за код построчно была, то и дополнительные операторы в строчке - доп. прибавка к пенсии ? гарантирована.
При быстрой отладке часто бесит, когда return происходит где-то в середине функции и начинаешь думать: "а что это сейчас было? ". Имхо, без return и goto посередине можно обойтись, делая функции покороче. Не более нескольких строк. Вынуждает более гранулярно именовать, поэтому многие и ленятся, лепят return посередине или даже goto
Мысли разумные. Нет плохих инструментов (языков, фреймворков), есть неуместные/неоптимальные в данной конкретной ситуации.
Что касается обработки ошибок с очисткой, с этим отлично справляется scope_exit (класс, которого несложно реализовать и самому). И читаемость прекрасная. Правда, для этого нужен C++.
С Си, конечно, сложнее. Вспомнилась функция pthread_cleanup_push, но тут появляются лишние сущности в виде функций.
Равзе можно говорить о goto и не привести ссылку на труд Запретный плод GOTO сладок (версия для микроконтроллеров)!
@avn ещё в 2011 году всё предвидел!
Ну почти все привёденные альтернативы без goto лучше. "Антипаттерн" со вложенными if как раз можно оспорить, что во многих случаях вложенные if это самое то. Вот в приведённом примере вложенные if лучше. В goto переставил кусок кода и всё сломалось, а в if будет на уровне компилятора выдана ошибка. Флаги - ещё лучше - код предельно понятный. Вложенные функции тоже свой плюс имеют, тут трудно приляпнуть ошибку.
И так, где goto допустимо, его оставили в виде return/exit... и т.д. break и т.д. и других специфических операторов.
Тем более в Паскале и ему подобных например вместо громоздкого
if (flag_1) {
flag_2 = init_stuff(bar);
}
было бы:
if flag_1 then flag_2 := init_stuff(bar);
Ну так и в C скобки не обязательны:
if (flag_1) flag_2 = init_stuff(bar);Видимо с каким-то C подобным языком перепутал , где нельзя без скобок.
if flag1 { flag_2 = init_stuff(bar); }Сколько было совершено ошибок из-за подобного (см. ниже) сочетания необязательных фигурных скобок, невнимательности и кривого форматирования — отдельный вопрос…
if (flag_1)
flag_2 = init_stuff(bar);
do_something(args);
Если бы goto было абсолютным злом, его бы не было в синтаксисе языков программирования - это необязательный элемент. Соответственно, раз оно есть, значит, в ряде случаев его использование удобно и оправдано.
Надеялся почитать аргументы за goto, а получил очередное перечисление недостатков C :/
Почему в Си внутри switch нельзя прыгать на его произвольную метку? Типа goto case 2
Кто знает, или есть какие-то предположения?
Можно. Но не на case'ы, а на метки внутри блоков (если не боишься отдельного котла в аду для таких)
А так свитч-кейз это по сути и есть "множественный условный гоу-ту". Мы ж не на "пимп май райд" чтобы засовывать гоу-то внутрь гоу-то, чтобы ты мог делать безусловный преход, когда ты делаешь условный переход?
Т.е. можно, но нельзя, о чём я и написал.
Мне пришлось делать именно такую дикость:
case 2:
_case2:
_do_something;
_break;
case 3:
_do_something;
_if(true) goto case2;
_do_something;
Э-э-э, зачем?
Это делается так:
case 3:
_do_something;
_if(false) _do_something;
_else brake;
case 2:
_do_something;
_break;Т.е. просето break в конце case-выражения не пишете и "проваливаетесь" дальше
А если у вас более сложная логика, то за такую её реализацию — пять лет расcтрелов без права переписки :)
Дейкстра 5 раз перевернулся в гробу ))
О вреде GOTO-фобии (с примерами на C)