Утверждение, гласящее, что если дана группа из 23 или более человек, то вероятность того, что хотя бы у двух из них дни рождения (число и месяц) совпадут, превышает 50 %. Для группы из 60 или более человек вероятность совпадения дней рождения хотя бы у двух её членов составляет более 99 %, хотя 100 % она достигает, только когда в группе не менее 366 человек (с учётом високосных лет — 367).
Такое утверждение может показаться противоречащим здравому смыслу, так как вероятность одному родиться в определённый день года довольно мала, а вероятность того, что двое родились в конкретный день — ещё меньше, но является верным в соответствии с теорией вероятностей. Таким образом, оно не является парадоксом в строгом научном смысле — логического противоречия в нём нет, а парадокс заключается лишь в различиях между интуитивным восприятием ситуации человеком и результатами математического расчёта.
Расчёт вероятности
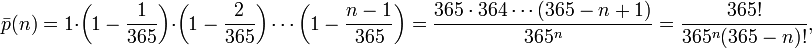
Тогда вероятность того, что хотя бы у двух человек из n дни рождения совпадут, равна

Значение этой функции превосходит 1/2 при n = 23 (при этом вероятность совпадения равна примерно 50.7 %). Вероятности для некоторых значений n иллюстрируются следующей таблицей:
Близкие дни рождения
Другое обобщение парадокса дней рождения состоит в постановке задачи о том, сколько человек нужно для того, чтобы вероятность наличия в группе людей, дни рождения которых различаются не более чем на один день (или на два, три дня и так далее), превысила 50 %. Эта задача более сложная, при её решении используется принцип включения-исключения. Результат (опять-таки в предположении, что дни рождения распределены равномерно) получается следующим:
Таким образом, вероятность того, что даже в группе из 7 людей дни рождения хотя бы у двух будут различаться не более чем на неделю, превышает 50 %.
Такое утверждение может показаться противоречащим здравому смыслу, так как вероятность одному родиться в определённый день года довольно мала, а вероятность того, что двое родились в конкретный день — ещё меньше, но является верным в соответствии с теорией вероятностей. Таким образом, оно не является парадоксом в строгом научном смысле — логического противоречия в нём нет, а парадокс заключается лишь в различиях между интуитивным восприятием ситуации человеком и результатами математического расчёта.
Расчёт вероятности
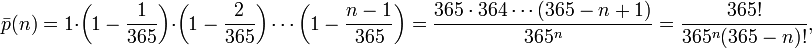
Тогда вероятность того, что хотя бы у двух человек из n дни рождения совпадут, равна

Значение этой функции превосходит 1/2 при n = 23 (при этом вероятность совпадения равна примерно 50.7 %). Вероятности для некоторых значений n иллюстрируются следующей таблицей:
- n — p (n)
- 10 — 12 %
- 20 — 41 %
- 30 — 70 %
- 50 — 97 %
- 100 — 99.99996 %
- 200 — 99.9999999999999999999999999998 %
- 366 — 100 %
Близкие дни рождения
Другое обобщение парадокса дней рождения состоит в постановке задачи о том, сколько человек нужно для того, чтобы вероятность наличия в группе людей, дни рождения которых различаются не более чем на один день (или на два, три дня и так далее), превысила 50 %. Эта задача более сложная, при её решении используется принцип включения-исключения. Результат (опять-таки в предположении, что дни рождения распределены равномерно) получается следующим:
- Максимальное различие дней рождения, дней Необходимое число людей
- 1 23
- 2 14
- 3 11
- 4 9
- 5 8
- 8 7
Таким образом, вероятность того, что даже в группе из 7 людей дни рождения хотя бы у двух будут различаться не более чем на неделю, превышает 50 %.
