Уменьшение размерности данных — это подход упрощения сложных наборов данных для облегчения их обработки. По мере того как данные растут и становятся более сложными, извлекать информацию становится все труднее, а визуализация становится более накладной. Методы уменьшения размерности данных решают эту проблему, предоставляя меньшее количество измерений (столбцов) при сохранении наиболее важной информации. Мы можем потерять некоторые детали, но получить более простое представление данных, которое легче обрабатывать и сравнивать.
Уменьшение размерности широко используется в области машинного обучения и анализа данных. Его цель состоит в том, чтобы упростить обработку данных за счет уменьшения количества объектов в наборе при сохранении ключевой информации. Когда мы сталкиваемся с данными большой размерности, ее уменьшение может помочь нам снизить вычислительную сложность, повысить производительность и результативность модели.
Чтобы проиллюстрировать методы уменьшения размерности данных в Python, возьмем набор данных red wine на kaggle. Поля набора данных описаны следующим образом:
fixed.acidity: fixed acidity (g /dm^3)
volatile.acidity: volatile acidity (g /dm^3)
citric.acid: citric acid (g /dm^3)
residual.sugar: residual sugar (g /dm^3)
chlorides: chlorides (g /dm^3)
free.sulfur.dioxide: free sulfur dioxide (mg /dm^3)
total.sulfur.dioxide: total sulfur dioxide (mg /dm^3)
density: density (g /cm^3)
pH: pH
sulphates: sulphates (g /dm3)
alcohol: alcohol (% by volume) Output variable (based on sensory data)
quality: quality (score between 0 and 10)
Загрузка данных:
import pandas as pd red_wine_df=pd.read_csv('/home/data/wineQualityReds.csv',index_col=0) red_wine_df #red_wine_df.columns

Проверяем, есть ли пустые значения в наборе данных, их нет:
red_wine_df.isnull().sum()
Далее необходимо стандартизировать данные и сопоставить каждый столбец с аналогичными диапазонами и шкалами. Это очень важно при непосредственном сравнении данных между разными столбцами.
from sklearn.preprocessing import StandardScaler from sklearn.cluster import KMeans scaler = StandardScaler() red_wine_df = pd.DataFrame(data = scaler.fit_transform(red_wine_df), columns = red_wine_df.columns) kmeans = KMeans(n_clusters = 3) cluster = kmeans.fit_predict(red_wine_df) __SNB_DisplayTable(red_wine_df)

Линейные методы
Линейный метод позволяет уменьшить размерность данных при сохранении наиболее важной информации. Он фиксирует исходные закономерности и линейные взаимосвязи в данных, предлагая способ их представления в пространстве меньшего размера. Основные линейные методы:
Principal Component Analysis (PCA)
Independent Component Analysis (ICA)
Truncated Singular Value Decomposition (TruncatedSVD)
PCA (Principal Component Analysis)
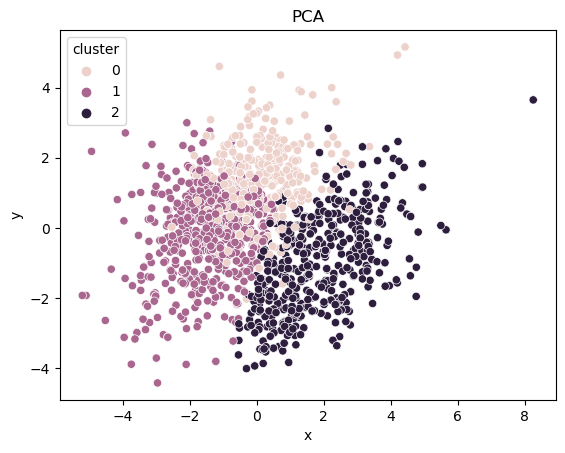
Анализ главных компонент (PCA) уменьшает размерность набора данных, максимизируя при этом дисперсию интерпретации каждого основного компонента. Как же понять PCA? В каждом наборе данных каждый столбец описывает определенный признак, в котором может содержаться значение алкоголя, значение рН, масса, плотность и т.д. Используя дисперсию как способ измерить степень колебания значений столбца, можно отметить объекты с большей дисперсией, что подразумевает содержание большей информации; объекты с дисперсией, равной 0, не предоставляют никакой информации, вот поэтому дисперсия является ключевым фактором.
Принцип работы PCA заключается в поиске сжатого представления исходных данных в меньшем измерении, максимизирующего общую дисперсию (или флуктуацию) исходных данных. Это означает, что общая схема по-прежнему сохраняется, при этом данные максимально упрощаются.
Код уменьшения размерности PCA выглядит следующим образом:
from sklearn.decomposition import PCA import seaborn as sns import matplotlib.pyplot as plt pca2D = PCA(n_components=2) #dimensions pca_2D = pca2D.fit_transform(red_wine_df) pca2D_df = pd.DataFrame(data = pca_2D, columns = ['x', 'y']) pca2D_df['cluster'] = cluster sns.scatterplot(x='x', y='y', hue='cluster', data=pca2D_df) plt.title("PCA") plt.show()
ICA (Independent Computing Architecture)
Целью анализа независимых компонент (ICA) является разделение смешанных сигналов на их исходные источники. В ICA мы предполагаем, что эти источники независимы друг от друга, то есть они не влияют друг на друга.
Давайте разберемся в этой концепции на простом примере. В нашем наборе данных есть 3 различных типа винных ароматов, и мы хотим разделить их на оригинальные сорта вин. Хотя в настоящее время вина смешиваются вместе, мы считаем, что они статистически независимы друг от друга. По сути, это означает, что если мы выпьем вино с одним вкусом, мы не получим никакой дополнительной информации о других вкусах вина. Предполагая, что каждый вкус независим, ICA как бы разблокирует (разделит) смешанное вино и восстановит его первоначальный вкус, даже если вы заранее ничего не знаете о смешанном вкусе или методе смешивания.
После выбора необходимого количества независимых ингредиентов (винных ароматизаторов) вы можете использовать их в качестве уменьшенного по размерам представления данных. Эти статистически независимые компоненты фиксируют различные аспекты исходных данных, тем самым обеспечивая уменьшенное по размерам представление.
Код ICA для уменьшения размера данных выглядит следующим образом:
from sklearn.decomposition import FastICA ica2D = FastICA(n_components=2) ica_data2D = ica2D.fit_transform(red_wine_df) ica2D_df = pd.DataFrame(data = ica_data2D,columns = ['x', 'y']) ica2D_df['cluster'] = cluster sns.scatterplot(x='x', y='y', hue='cluster', data=ica2D_df) plt.title("ICA") plt.show()

TruncatedSVD (Truncated Singular Value Decomposition)
TruncatedSVD (усеченная декомпозиция сингулярных значений) является особенно эффективным методом уменьшения размерности при обработке больших наборов данных. Он тесно связан с анализом главных компонент (PCA) и даже может рассматриваться как вариант PCA, хотя этот метод лучше подходит для создания плотных представлений из разреженных матриц (то есть матриц со многими нулевыми элементами).
TruncatedSVD код для уменьшения размерности выглядит следующим образом:
from sklearn.decomposition import TruncatedSVD tsvd2D = TruncatedSVD(n_components=2) tsvd_data2D = tsvd2D.fit_transform(red_wine_df) tsvd2D_df = pd.DataFrame(data = tsvd_data2D, columns = ['x', 'y']) tsvd2D_df['cluster'] = cluster sns.scatterplot(x='x', y='y', hue='cluster', data=tsvd2D_df) plt.title("TruncatedSVD") plt.show()

Нелинейные методы
Методы уменьшения нелинейной размерности пытаются зафиксировать более сложные нелинейные взаимосвязи в данных и представить их в виде пространств меньшей размерности. Три наиболее часто используемые схемы трехмерного нелинейного уменьшения размеров:
MDS(Multidimensional Scaling)
T-SNE (t-Distributed Stochastic Neighbor Embedding)
UMAP
MDS(Multidimensional Scaling)
MDS (многомерное масштабирование) — это метод, используемый для визуализации сходства или различия между наблюдениями в наборе данных. В этом представлении похожие наблюдения расположены ближе друг к другу, в то время как непохожие разделены большим расстоянием. Многомерное масштабирование обладает преимуществами линейного и нелинейного уменьшения размерности, в зависимости от используемых настроек и алгоритмов. Во всех случаях многомерное масштабирование направлено на поддержание расстояния между точками данных, гарантируя, что представление с уменьшением размерности сохранит эти расстояния.
Код для уменьшения размерности с помощью MDS выглядит следующим образом:
from sklearn.manifold import MDS mds2D = MDS(n_components=2) mds_data2D = mds2D.fit_transform(red_wine_df) mds2D_df = pd.DataFrame(data = mds_data2D, columns = ['x', 'y']) mds2D_df['cluster'] = cluster sns.scatterplot(x='x', y='y', hue='cluster', data=mds2D_df) plt.title("MDS") plt.show()

t-SNE (t-Distributed Stochastic Neighbor Embedding)
t-SNE (стохастическое вложение соседей с t-распределением) — это алгоритм, используемый для упрощения и визуализации сложных данных. Он достигает этой цели путем сравнения сходства между точками данных в исходном пространстве высокой размерности и пространстве низкой размерности. Затем он создает распределение вероятностей для представления этих сходств, стремясь сделать их как можно более похожими. Алгоритм итеративно корректирует положение точек данных в низкоразмерном пространстве до тех пор, пока распределение не станет максимально близким.
Одна вещь, которую следует отметить в t-SNE, заключается в том, что она больше фокусируется на сохранении локальных связей, чем глобальных. Это означает, что точки данных, расположенные близко друг к другу в исходном многомерном пространстве, скорее всего, останутся близкими в уменьшенном по размерам представлении. Однако общее расстояние между точками может не сохраняться. Этот компромисс позволяет t-SNE выделять локальные закономерности и кластеры, что делает его очень полезным при визуализации сложных данных.
Код для уменьшения размерности t-SNE выглядит следующим образом:
from sklearn.manifold import TSNE tsne2D = TSNE(n_components=2) tsne_data2D = tsne2D.fit_transform(red_wine_df) tsne2D_df = pd.DataFrame(data = tsne_data2D, columns = ['x', 'y']) tsne2D_df['cluster'] = cluster sns.scatterplot(x='x', y='y', hue='cluster', data=tsne2D_df) plt.title("T-SNE") plt.show()

UMAP (Uniform Manifold Approximation and Projection)
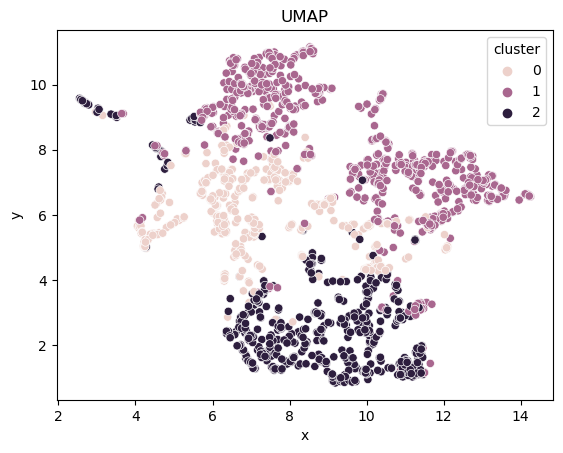
Uniform Manifold Approximation and Projection (сокращенно UMAP) UMAP можно рассматривать как более мощного родственника t-SNE.Он также изучает нелинейные отображения для поддержания целостности кластера, и это происходит быстрее. Кроме того, по сравнению с t-SNE, UMAP, как правило, лучше справляется с поддержанием глобальной структуры данных. В этом контексте глобальная структура относится к «степени близости» между похожими типами вин, в то время как локальная структура относится к степени кластеризации одного и того же типа вина в уменьшенном по размерам пространстве.
Код для уменьшения размерности UMAP выглядит следующим образом:
#pip install umap-learn from umap.umap_ import UMAP umap2D = UMAP(n_components=2) umap_data2D = umap2D.fit_transform(red_wine_df) umap2D_df = pd.DataFrame(data = umap_data2D,columns = ['x', 'y']) umap2D_df['cluster'] = cluster sns.scatterplot(x='x', y='y', hue='cluster', data=umap2D_df) plt.title("UMAP") plt.show()
Представление схемы всего примера:

Эти примеры — лишь малая часть методов уменьшения размерности, но они очень полезны при работе со сложными наборами данных. Следует отметить, что уменьшение размерности не является решением для всех ситуаций; наиболее сложная часть — определение того, какой метод использовать, исходя из характера данных и конкретных проблем, или того, требуется ли вообще использование какой-либо техники уменьшения размерности.
