MarkWatney 14 ноя 2023 в 12:00

Обучение с блэкджеком и подкреплением. Ищем оптимальную стратегию игры

Средний

8 мин

4.1K

Туториал

Предположим у нас благородная цель - мы хотим разорить казино, чтобы оно не разоряло других, а попутно заработать самим. В качестве цели выберем игру блэкджек. Эта игра довольно сильно зависит от случайности, но в перспективе, если придерживаться одной стратегии, то мы всегда придем к одному конкретному выигрышу или проигрышу. И одна стратегия даст результат больше, чем другая. В этой статье я расскажу, как, используя обучение с подкреплением, найти лучшую, оптимальную стратегию на примере игры блэкждек.

Обучение с подкреплением (reinforcement learning) не зависит от того, где мы ее применяем. Это значит, что нам не нужно учитывать правила и нюансы игры, всю необходимую информацию мы получим из статистики. Для начала опишем общие принципы обучения с подкреплением.

Общая постановка задачи

Начнем с постановки задачи. Наша цель - обучить субъект (бота) взаимодействовать со средой (environment) таким образом, чтобы получить максимальную награду (rewards) от нее. Субъект, называется агентом (agent). Взаимодействует со средой он выполняя какие-то действия (actions). Например, если агент забивает гол противнику, то получает +1 в качестве награды, а если пропусти гол, то получит -1. Награда может быть отложенной во времени, т.е. нужно совершить определенное количество действий, прежде чем получится прийти к положительному результату. Т.е. в один момент времени агент может, например, получить штраф, но зато это приведет к большей награду в будущем. Каждый момент времени агент получает от среды вектор наблюдений (observations). Из вектора наблюдений агент формирует состояние агента (agent state), это состояние он отправляет в свою стратегию (policy) и получает от нее следующее действие, которое он совершит в следующий момент времени. Вектор наблюдений отличается от вектора состояния агента тем, что наблюдения могут быть неполными, а также вектор состояния агента может состоять, например, из векторов наблюдений, собранных в разные моменты времени. Короче говоря, вектор состояния агента - это вся информация, которая необходима агенту, чтобы, используя свою стратегию, получить следующее действие. В дальнейшем, состояние агента мы будем назвать просто состоянием (state). В итоге агент взаимодействует с миром по следующей схеме:

Состояние будет содержать полную необходимую информацию, чтобы получить следующее состояние. Таким образом мы описали модель нашего мира. Фактически мы описали марковский процесс принятия решений (Markov Decision Process — MDP). Следует ещё упомянуть, что чаще всего мы имеем дело со случайными процессами, попав дважды в одно и то же состояние и выполнив одно и тоже действие, мы тем не менее можем оказаться, например, либо в состоянии , либо в состоянии из-за стохастической природы нашей среды. Или она может быть на своем базовом уровне не случайной, но мы не в состоянии полностью ее описать и постоянно имеем какую-то ошибку, и в результате среда все равно становиться для нас стохастической.

Общей целью получить максимальную награду: $E[\sum{r_t}] \rightarrow max$ , где t - момент времени, - награда в момент времени t, - мат ожидание. Мы используем мат ожидание здесь, потому что одни и те же действия приведут к разному результату, и нас интересует средний выигрыш.

Q-Learning

Это игра довольно сильно зависит от случайности, тем не менее, есть набор правил - стратегия, которая в перспективе будет давать больше, чем если им не следовать. Стратегия с самым большим средним выигрышем будет называться оптимальной стратегией, именно ее нам и нужно будет найти.

На всякий случай напомню правила. Цель игры - обыграть дилера. Алгоритм игры следующий:

Дилер кладет себе одну карту, а затем две карты игроку. Каждая карта соответствует определенному количеству очков. Карты с цифрами (2 - 10) получают количество очков, равное своей цифре, карты с картинками (дама, валет, король) - 10, туз - 1 или 11, в зависимости от того, что выгоднее владельцу карты. Очки, полученные с карт, суммируются.
У игрока есть выбор - взять еще карту или нет. А потом еще одну. И так пока игрок не примет решение остановиться, или игрок получил количество очков больше 21.
Если игрок получил количество очков больше 21, то он проиграл.
Далее дилер берет себе еще карты, до тех пор, пока не наберет сумму очков большую или равную 17. Если дилер получил количество больше 21 - он проиграл.
Если у игрок получил больше очков, чем дилер, то он выиграл. Иначе игрок проиграл.
Правила игры могут немного меняться. И в нашей версии, если первым ходом игрок набрал 21, то он сразу выиграл.
(*Правила упрощены, мы же все-таки не собираемся на самом деле разорять казино?)

В качестве симулятора игры удобно использовать готовую реализацию в питоновской библиотеки ~~gym~~ gymnasium, которая специально создана для тестирования алгоритмов обучения с подкреплением.

В этом случае агент - это игрок. Возможны всего два действия - взять карту или остановиться. Таким образом, пространство действий (action space) состоит всего из двух возможных действий.

А нашим наблюдением и оно же состоянием будет количество очков у игрока и у дилера. Нам не важно, какие конкретно карты у нас и у дилера на руках, имеет значение только сумма очков. Можно также заметить, что если у игрока количество очков будет меньше 12, то он может спокойно просить еще карту, не боясь получить перебор. Поэтому варианты, где у игрока меньше 12 очков, мы рассматривать не будем. Особым случаем является наличие у игрока туза. Туз может считаться за 11 очков, но в случае перебора он станет единицей. Выделим его наличие как особый параметр, но если он привел к перебору, отнимаем у игрока 10 очков, и считаем, что у него больше нет туза ради упрощения. Подытожим наше пространство состояний (state space):

Количество очков у игрока - от 12 - 21
Наличие у игрока туза, если считается за 11 очков
Количество очков у дилера - от 1 до 10. 1 - это туз.

Если игрок после выполнения действия (попросить ещё карту, или решить остановиться) выигрывает, то он получает награду 1. Если проигрывает, то -1. Если у дилера и игрока поровну, то 0. Игра может состоять из нескольких ходов игрока, т.е. он может взять несколько карт. Если он взял карту и не получил перебор, то он на этом ходе получает 0.

Прежде чем мы перейдем к поиску оптимальной стратегии, интуитивно попробуем придумать свою хорошую стратегию. Предлагаю для начала рассмотреть такую

Если у нас есть туз, и меньше 20 очков, то берем еще карту. Иначе останавливаемся.
Без туза берем еще карту, только если очков меньше 16, так как вероятность перебора возрастает.

Как теперь оценить насколько хороша эта стратегия и насколько вероятно, что мы в итоге будем в плюсе? Сделаем симуляцию игры, проведем сто тысяч испытаний и посмотрим, сколько выигрыша в среднем она нам принесёт. Т.е. $R=\sum_{t} r_t, \space E[R] = \frac{\sum_{i}^{N}{R_i}}{N}$ . Получили -0.092. Мы в минусе, хоть и небольшом, а значит нужно искать стратегию получше. Для этого рассмотрим нашу стратегию поподробнее. Делая один шаг в игре, мы переходим из состоянияв состояние $state_{t+1}$ . Заведём табличку, где в каждая ячейка - это информация по каждому состоянию. В ячейке мы заведем счетчик (сколько раз мы прошли это состояние) и также будем хранить суммарную награду, которую мы получали из этого состояния. Т.е. проигрываем эпизод игры, проходим несколько состояний, по завершению обновляем счетчики и записываем сколько награды мы получили, начиная с данного состояния. Получим табличку, в которой каждый элемент будет описывать насколько выигрышное состояние мы имеем для нашей стратегии $\pi$ . Таким образом мы опишем так называемую value-функцию (value-function).

Кстати, можно заметить, что имеем дело с большими числами, а значит время подумать о численной стабильности. Чтобы избежать суммирования, лучше перейти к итеративному обновлению: $V(state)_{i+1} = V(state)_i \cdot \frac{N}{N+1} + G_{i+1} \cdot \frac{1}{N+1} = V(state)_i + \frac{1}{N+1} \cdot (G_{i+1} - V(state)_{i})$ , где $G_{i+1}$ - награда, полученная из состояния . В итоге формулу можем записать так: $V(state)_{i+1}=V(state)_i+\alpha \cdot (G_{i+1} - V(state)_i), \space где \space \alpha = \frac{1}{N+1}$ . Можно заметить, что $\alpha$ постепенно уменьшается ростом числа экспериментов. Мы можем сразу оставить ее как достаточно малую константу, тогда мы получим в качестве обновления не простое среднее, а обновление через экспоненциальное скользящее среднее. Этот вариант тоже будет работать, но обновляться будет более плавно и будет постепенно забывать старые данные в пользу более новых, что может быть полезным свойством.

Для расчета нашей value-фнукции приходится запоминать состояния и награды и ждать завершения эпизода игры. Но есть способ, при котором нам это делать не нужно, а кроме этого ускоряется сходимость. А значит требуется меньшее количество проигрываемых эпизодов. Мы описывали значение V-функции как: $V(state_t) = E[r_t + r_{t+1} + .. + r_n]$ , где - награда на шаге t, $r_{t+1}$ - на шаге t+1, и т. д. Если рассматривать конкретно игру блэкждек, то все награды будут нулевыми, кроме последнего шага. Однако, здесь блэкждек - это частная задача, а подход может быть применим для куда более широкого круга задач, поэтому оставляем обобщение. На каждом шаге мы переходим из состояния в состояние $state_{t+1}$ в соответствии с MDP. Но по идее у нас уже есть какая-то априорная оценка состояния t+1. Используем ее сразу для обновления , тогда получаем новую формулу: $V(state_t) = r_t + V(state_{t+1})$ , если t - это момент завершения игры, то просто , тогда $G_{i+1} = r_{t} + r_{t+1} + .. + r_n$ из предыдущей формулы станет: $G_{i+1} = r_t + V(state_{t+1})$ . Таким образом мы сможем обновлять значения V-функции на каждом шаге игры. Такая V-функция говорит нам сколько мы потенциально выиграем, находясь в данный момент в данном состоянии.

Если визуализировать расчет value-функции по нашей стратегии, то получим вот это:

Здесь два графика, потому что "у игрока есть туз" и "нет туза" - это два разных состояния. Оси player и dealer описывают количество очков у игрока и дилера, т.е. оси x, y - описывают состояние. А значения по оси z - это средний выигрыш, который мы ожидаем из данного состояния. Можно заметить, что вероятность выиграть дилера выше, когда у игрока 16 и выше. Если меньше, то нам нужно брать новую карту и тут мы можем получить перебор.

Если бы могли делать ставку в том момент, когда карты уже на столе, то сверяясь с нашей табличкой V, мы бы могли делать ставку только тогда, когда значение в ней выше нуля. Таким образом мы бы почти гарантировано вышли в плюс. Но эта табличка не говорит нам, как нам улучшить нашу стратегию. Для этого мы можем построить еще одну более подробную табличку. Она будет учитывать не только текущее состояние, но и действие, которое мы совершаем: $Q(state_t, action) = E[r_t + V(state_{t+1})]$ . Эта Q-таблица, по аналогии с V-функцией, будет описывать Q-функцию. Теперь подумаем, как мы можем улучшить нашу стратегию, использовав Q-таблицу. Допустим мы находимся в состоянии . В соответствии с нашей стратегией мы, допустим, должны сделать действие . Но, если посмотреть на таблицу Q, то мы видим, что . Совершив действие мы по нашим ожиданиям придем к большему выигрышу. Тогда скорректируем нашу стратегию. Только после обновления стратегии мы должны также обновить V и Q-функции, так как они были привязаны к нашей предыдущей стратегии. Получается слишком много вычислений. Мы можем сократить их число, если будем обновлять все сразу. Алгоритм будет следующий:

Проинициализируем таблицу Q случайными числами или нулями
Находясь в состоянии , перебираем значения в таблице Q по этому состоянию, и выбираем то, в котором у нас большее значение. Т.е. выбираем то действие, которое по нашей текущей статистике даст лучший результат. Т.е. $\pi(state) = argmax_{action}Q(stat, action)$ .
Из Q-функции мы можем получить V-функцию:
$V(state) = \max_{action}Q(state, action)$ .
Для Q-таблицы должно будет выполняться следующие условия:
$Q(state_t, action_t) = E[r_t + V(state_{t+1})] = E[r_t + \max_{action}Q(state_{t+1}, action)]$
Чтобы к ним постепенно прийти к ним, будем постепенно обновлять текущие значения также, как мы делали это для вычисления V-таблицы:
$Q(state_t, action_t)_{i+1} = Q(state_t, action_t)_i + \alpha \cdot (r_t + \max_{action}Q(state_{t+1}, action)_i - Q(state_t, action_t)_i)$ Для состояний, где игра заканчивается, $state_{t+1}$ существовать не будет, поэтому:
$Q(state_t, action_t)_{i+1} = Q(state_t, action_t)_i + \alpha \cdot (r_t - Q(state_t, action_t)_i)$ .

Обновляя Q-функцию (она же таблица Q), мы обновляем и политику и V-функцию. А формула $Q(state_t, action_t) = E[r_t + \max_{action}Q(state_{t+1}, action)]$ - это практически формула оптимальности Беллмана, но с некоторыми нюансами, которые мы здесь рассматривать не будем.

Таким образом мы можем найти оптимальную стратегию. С каждой новой итерацией игры мы всё больше уточняем статистику и приближаемся в правильному решению. Но использовать полученную статистику мы начинаем сразу, до того как она стала достаточно точной. Получив на определённых ходах плохие результаты, мы больше не будем их повторять. А может так получиться, что в перспективе именно они приводят к лучшему результату. Это называют exploration-exploitation дилеммой. Чтобы избежать этой проблемы, используют, например, epsilon-greedy стратегию. Она заключается в следующем - мы вводим параметр $\epsilon$ , который в процессе наших вычислений меняется от достаточно большого числа до достаточно малого. Например, от 1 до 0. Далее, когда мы делаем ход, мы выбираем случайное число от 0 до 1 из равномерного распределения. Если полученное число меньше $\epsilon$ , то следующее действие мы выбираем случайным образом, иначе выбираем следующее действия исходя из нашей жадной стратегии: $action=argmax_{action}Q(state, action)$ . Таким образом мы будем переходить от абсолютно случайно стратегии до нашей жадной. И случайная стратегия на начальному этапе даст на возможность собрать более адекватную статистику.

Как уже писал выше, из Q можно получить нашу V-функцию и нашу стратегию - по Q мы выбираем такое действие, которое даст нам наибольший выигрыш. Если визуализировать V-функцию в то время, как сходится наша Q-функция, то получим вот это:

А полученная стратегия выглядит вот так:

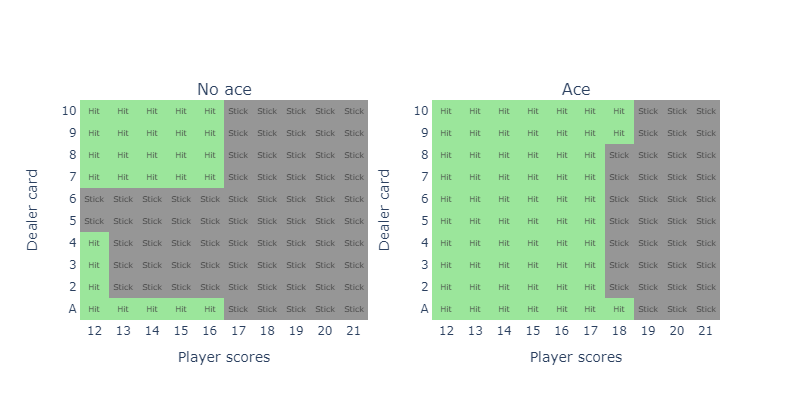
Оценим наш выигрыш, проделав 100000 симуляций игры с нашей стратегией:

Получилось -0.046. Мы улучшили результаты в два раза, но все равно остались в минусе. Значит в любом случае выиграет дилер. Я знал, что с этими казино что-то не так! План по разорению казино отменяется. Тем не менее мы рассмотрели метод, который никак не связан конкретно с игрой блэкджек или карточными играми в принципе. Метод называется Q-learning и его можно применить для самых разных других задач.

Код примера находится здесь.

У библиотеки gymnasium есть свой туториал с блекджеком. Их стратегия получилась очень похожей на мою, но есть различие в паре ячеек. Это вероятно связано с тем, что в методе присутствует небольшая степень случайности, а в некоторых позициях просто нет разницы (или практически нет) между тем, чтобы взять карту или остановиться.

Теги:

Хабы:

Обучение с блэкджеком и подкреплением. Ищем оптимальную стратегию игры

Общая постановка задачи

Q-Learning

Публикации

Истории

Работа

Ближайшие события