danisgrpv 12 ноя 2023 в 17:35

Обработка результатов статистических наблюдений с помощью толерантных интервалов

Простой

11 мин

4.2K

Толерантные интервалы

При определении понятия толерантного интервала, в качестве примера, будем рассматривать функцию плотности вероятности стандартного нормального распределения. На рисунках 1 и 2 изображены квантили распределения - значения, которые случайная величина не превышает с заданной вероятностью или

$\int_{-\infty }^{x_{p}}f(x)dx=P \tag{1}$

где - функция плотности вероятности распределения, - квантиль, соответствующий значению вероятности .

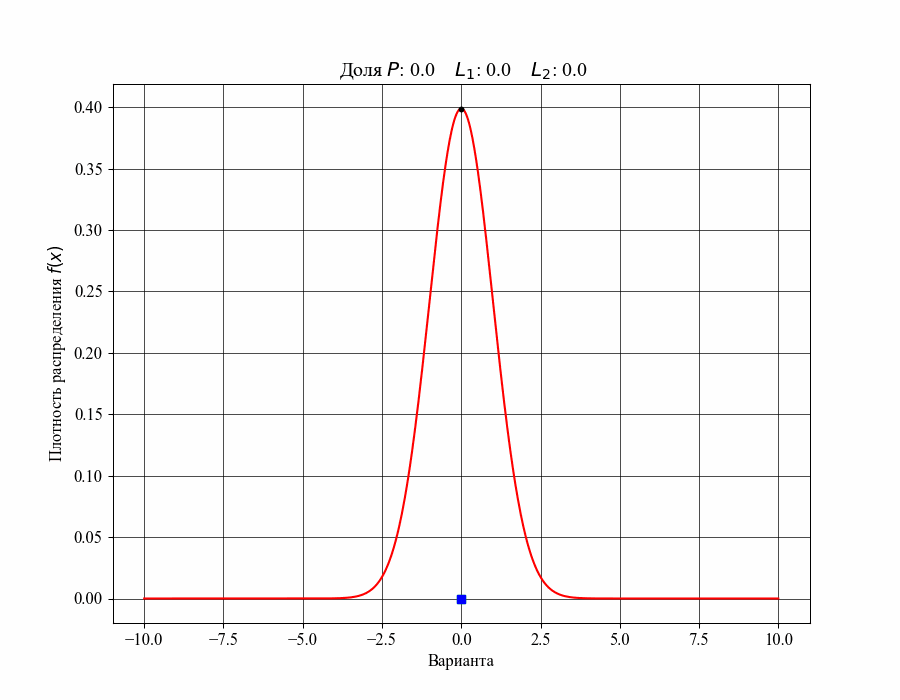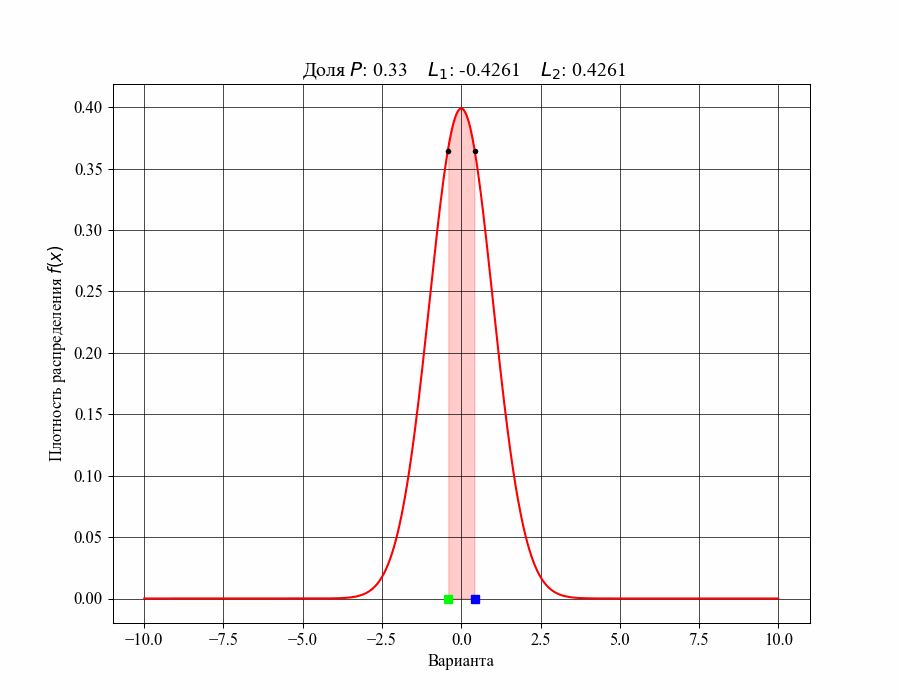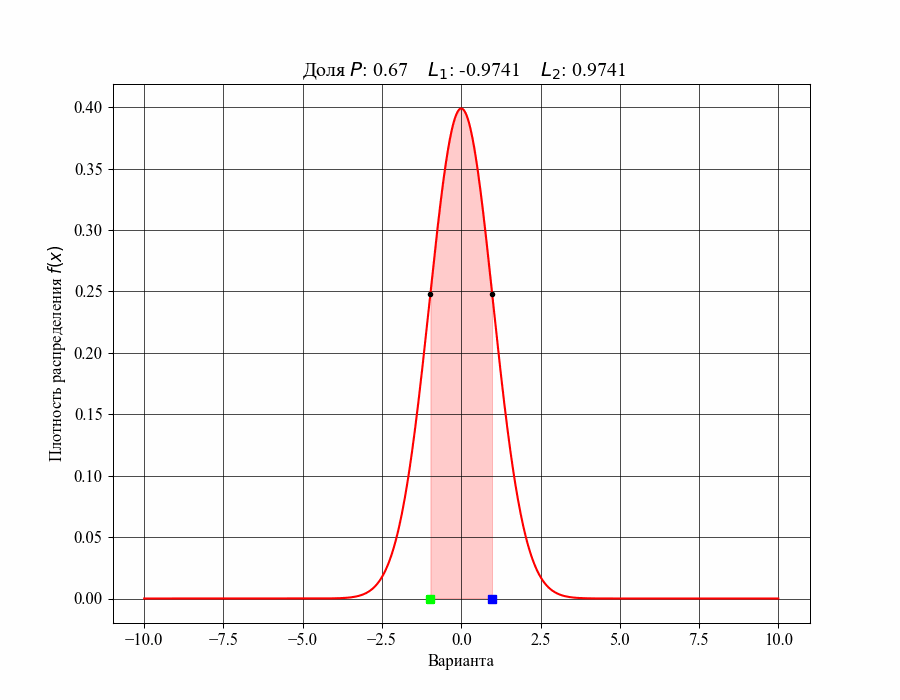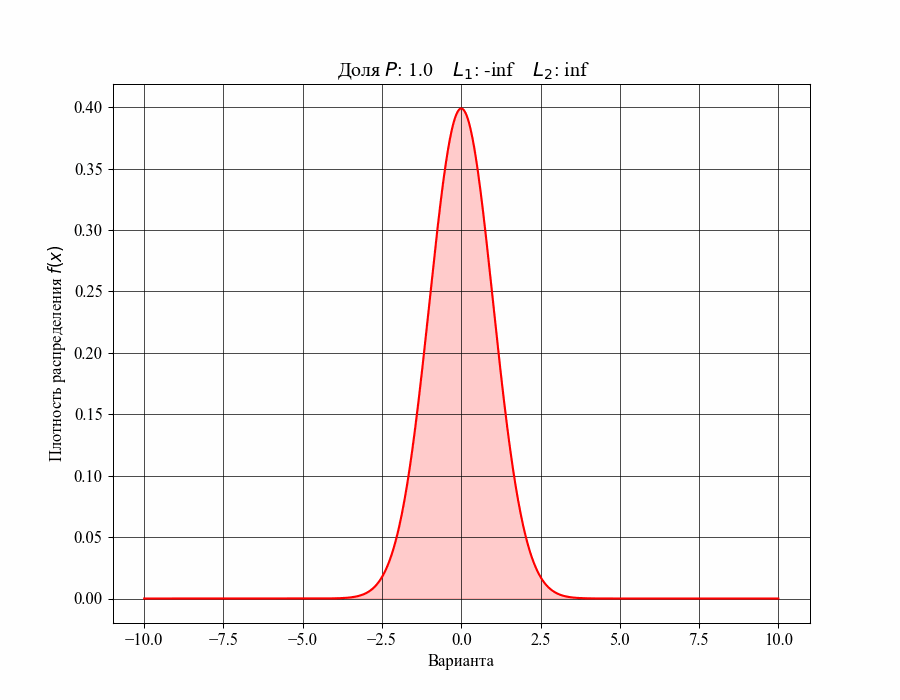
Иллюстрация к данному соотношению, где черный квадрат - соответствующий квантиль распределения:

Рисунок 1 - Вероятность, соответствующая -му квантилю распределения — Рисунок 1 - Вероятность, соответствующая $x_{p}$ -му квантилю распределения

Рисунок 2 - Вероятность, соответствующая -му квантилю распределения — Рисунок 2 - Вероятность, соответствующая $x_{p}$ -му квантилю распределения

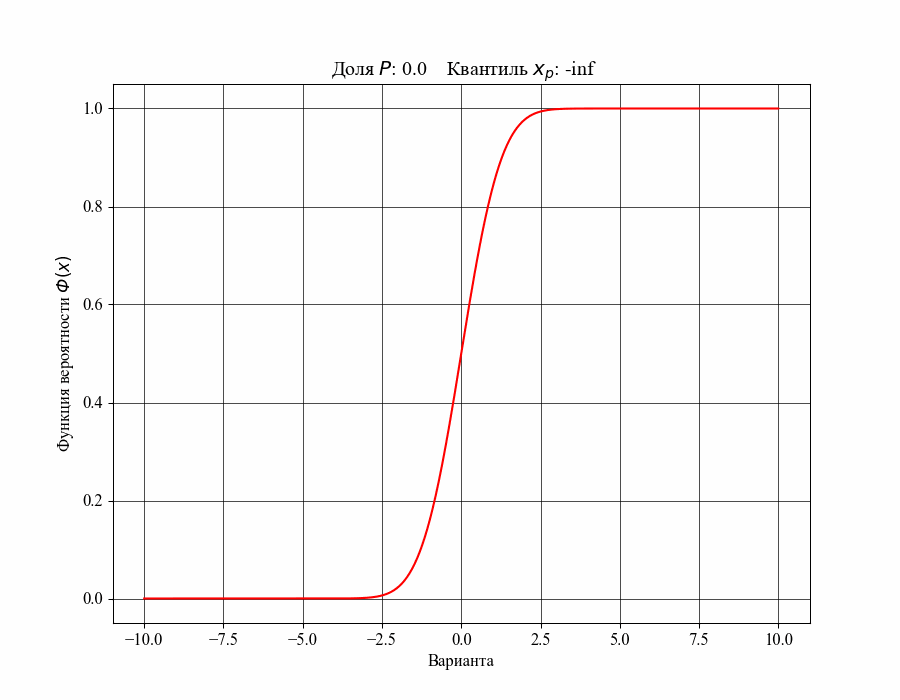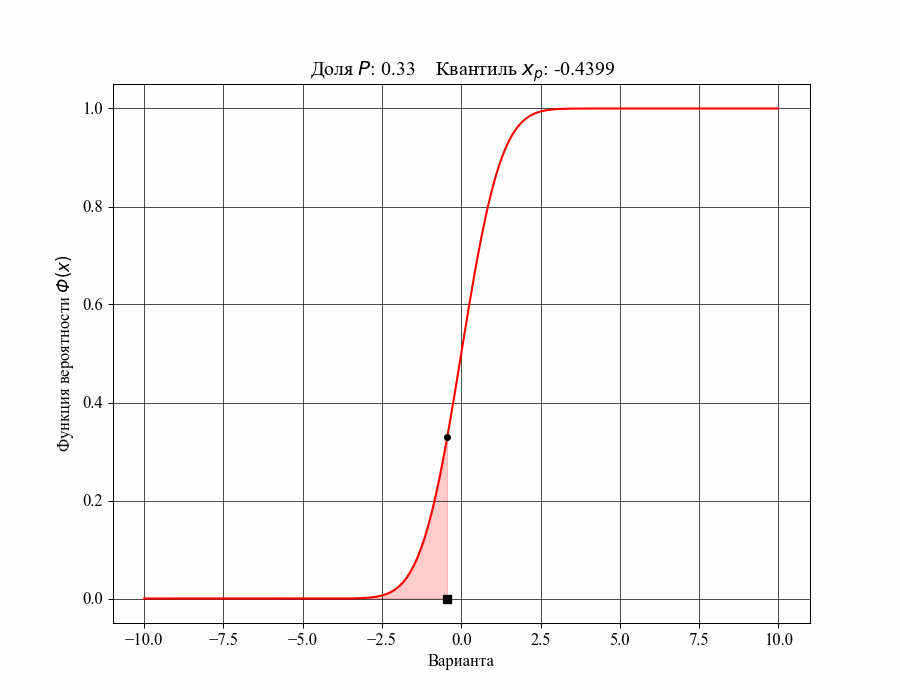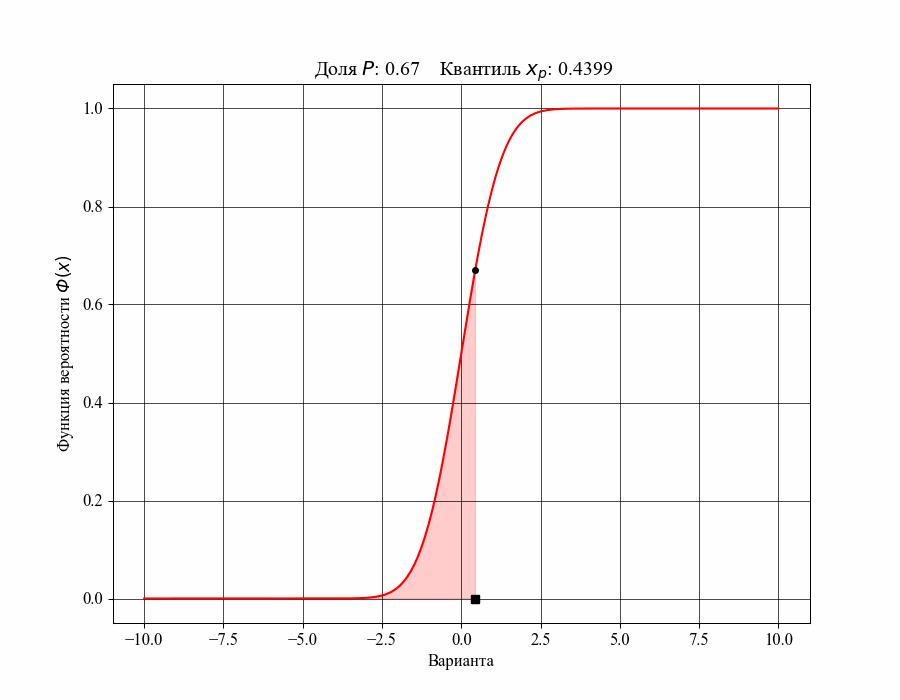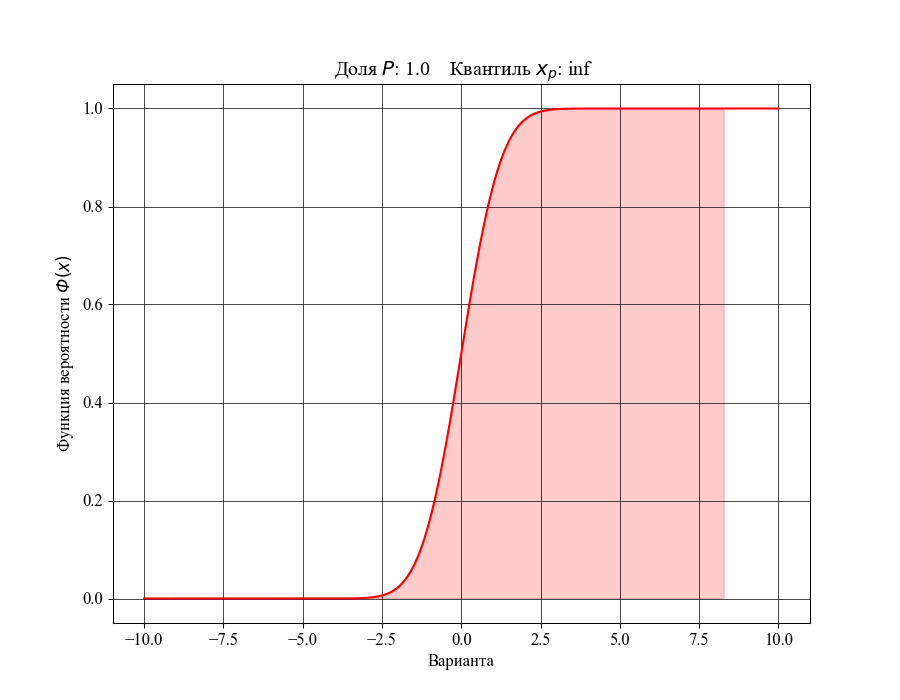
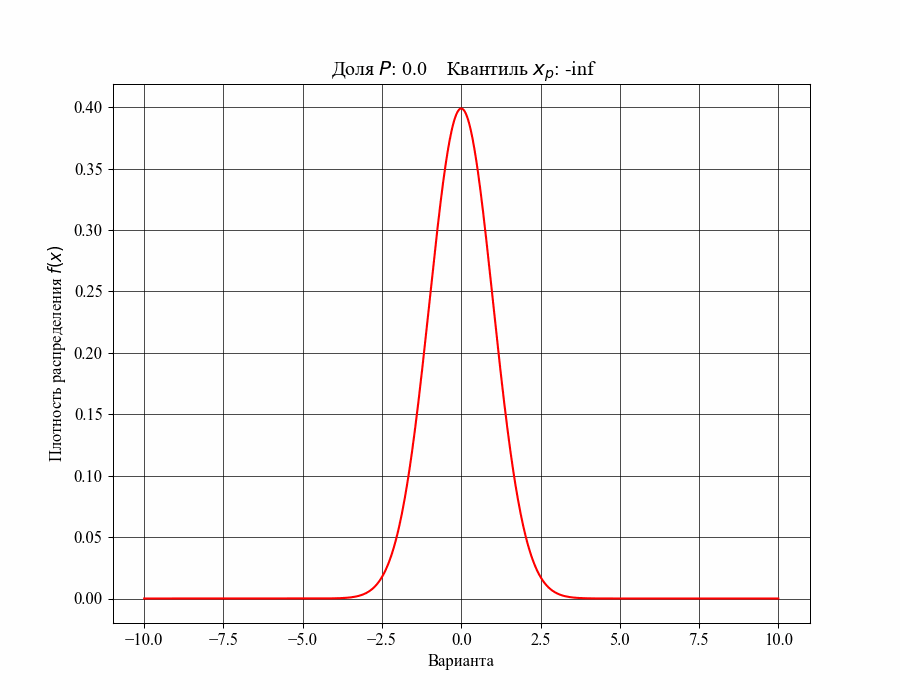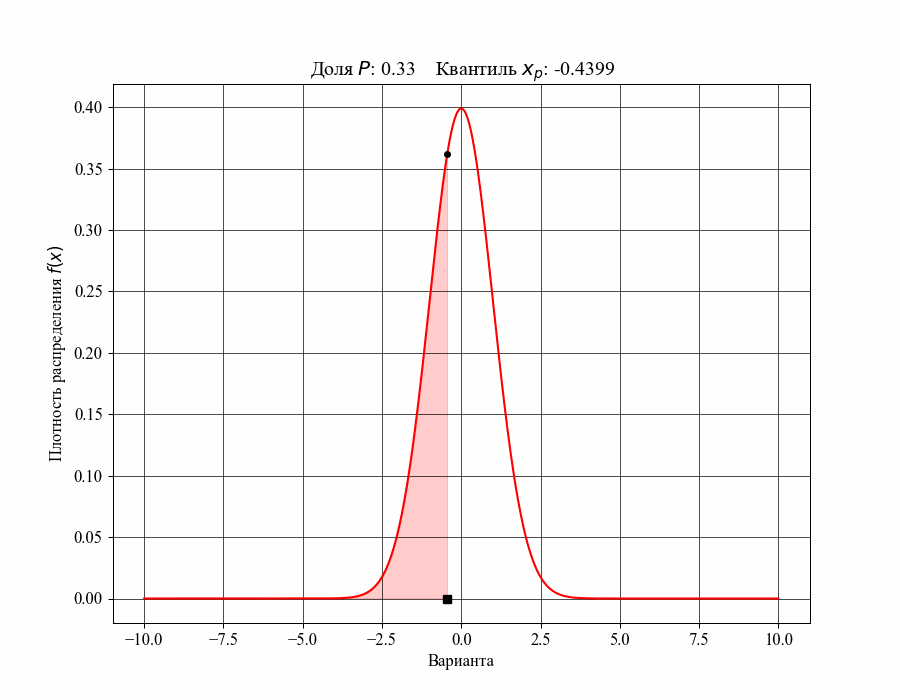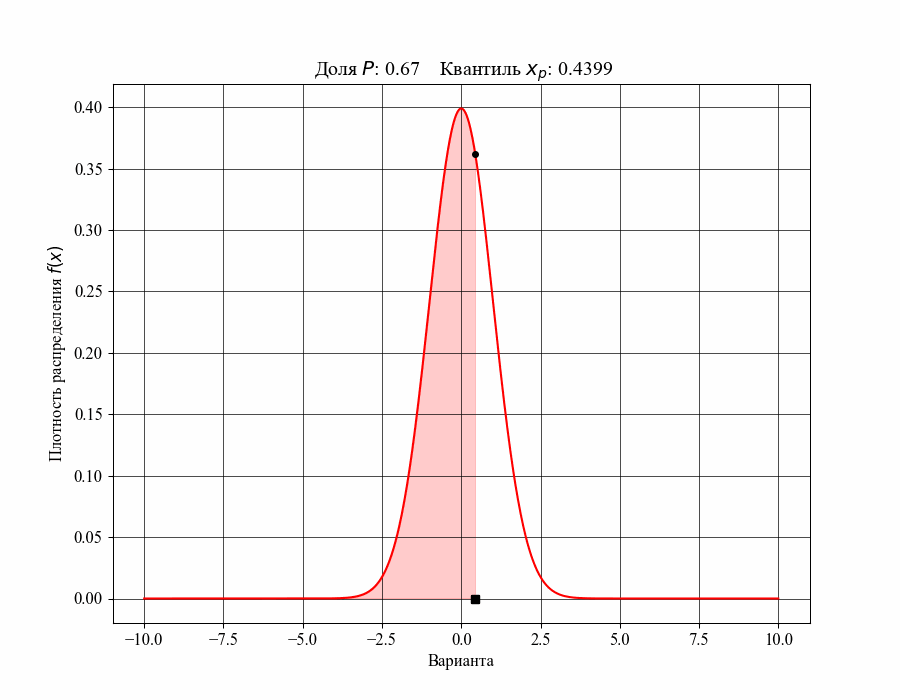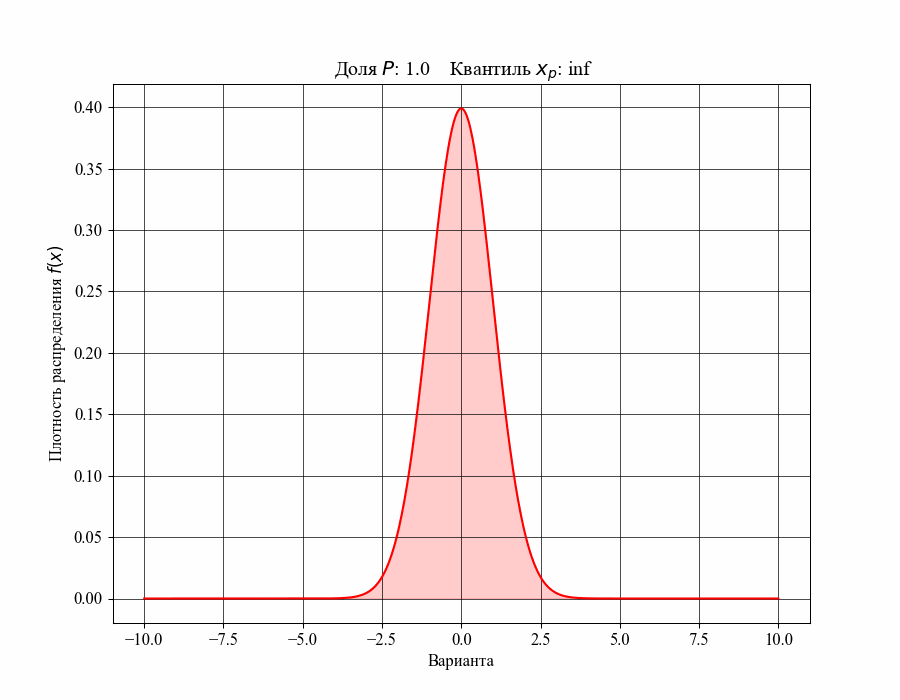
Таким образом, можно сказать, что квантиль распределения представляет собой границу, ниже которой расположена долясоответствующего распределения. Аналогично, долю распределения внутри некоторого интервала, обе границы которого конечны, можно определить как:

$\int_{x_{p_1} }^{x_{p_2}}f(x)dx = P_2 - P_1 \tag{2}$

где $x_{p_1,p_2}$ - меньший и больший квантили, соответственно.

Можно переписать данное выражение в другой форме

$Ф(x_{p_{2}}) - Ф(x_{p_{1}}) = P_2 - P_1 \tag{3}$

где - функция распределения.

Меньший и больший квантили назовем нижней и верхней границами соответствующего интервала, например $L_{1,2}$ . Ниже на рисунке 3 можно увидеть как изменяется доля распределения, содержащаяся внутри интервала, при изменении его ширины, то есть в зависимости от значений соответствующих границ (нижняя граница обозначена зеленым квадратом, верхняя - синим)

Рисунок 3 - Зависимость доли распределения внутри интервала от его границ

Перейдем непосредственно к определению понятия толерантного интервала. В Википедии, со ссылкой на соответствующую литературу, пишут:

Толерантный интервал является интервалом в выборочном пространстве наблюденных случайных величин. Он определяется достаточной статистикой на основе требования о том, чтобы при заданном доверительном уровне содержать вероятностную меру статистического распределения, не меньшую заданного уровня.^[1]
Доверительный интервал определяется для некоторого параметра функции распределения и является интервалом в параметрическом пространстве. Он определяется достаточной статистикой на основе требования о том, чтобы вероятность того, что он содержит истинное значение неизвестного параметра была не меньше доверительного уровня.^[1]
[1] Закс, 1975

Толерантные интервалы являются по своему смыслу доверительными интервалами, но не для параметров, явно участвующих в задании распределения случайных чисел, а для самих функций распределения. До настоящего момента мы еще не упоминали о доверительном уровне (или уровне доверия), который фигурирует в приведенных определениях. Поскольку речь идет о случайных величинах, то какие-либо утверждения необходимо делать в вероятностной форме. Итак, еще раз дадим определение толерантного интервала: толерантный интервал - это интервал, между границами которого с заданной вероятностью содержится доля распределения не меньшая заданной.

Стоит акцентированно отметить важную особенность толерантного интервала, а именно то, что толерантный интервал содержит в себе некоторую долю распределения, то есть долю всей генеральной совокупности, хотя строится он на основании выборочных значений.

Для дальнейшего использования введем обозначения. Долю совокупности (2), содержащуюся внутри интервала, переобозначим как:

$A=\int_{L_{1} }^{L_{2}}f(x)dx \tag{4}$

и будем называть ее - доля накрытия. А вероятность, с которой данная доля (4) превышает некоторую заданную, будем называть уровнем доверия $\gamma$ . Тогда в математической форме, определение толерантного интервала можно записать как:

$P\left\{ A(L_{1}, L_{2})\ge \beta \right\}=\gamma \tag{5}$

где $\beta$ - требуемая доля накрытия генеральной совокупности толерантным интервалом с заданными границами.

Как уже говорилось, толерантный интервал строится на основании выборки некоторого размера , поэтому нам необходимо найти выборочные оценки соответствующих статистик (в случае нормального закона распределения - математического ожидания и стандартного отклонения). В таком случае, границы интервала можно определить как:

$\begin{matrix} L_1=\hat{\mu} - k_1\cdot \hat{s} \\ L_2=\hat{\mu} + k_2\cdot \hat{s} \end{matrix} \tag{6}$

Из соотношения (6) видно, что соответствующие границы являются случайными числами. Поэтому, чтобы определить уровень доверия к доле накрытия генеральной совокупности толерантным интерваломмы должны многократно повторить следующие процедуры:

Извлечение выборки заданного размера из генеральной совокупности;
Нахождение оценок необходимых статистик (в общем случае - параметры сдвига и масштаба распределения);
Вычисление соответствующих границ толерантного интервала;
Вычисление доли генеральной совокупности внутри интервала.

Находя долю интервалов, для которых выполняется условие $A \ge \beta$ мы получим соответствующий уровень доверия.

Уровень доверия - предел доли интервалов, накрывающих долю выбранной совокупности не менее заданной, при бесконечном повторении метода.^[2]
[2] [ГОСТ Р 50779.10—2000, статья 2.61 ]

Другими словами:

$\gamma = \lim_{N \to \infty } \frac{\left| \left\{ S \right\} \right|}{\left| \left\{ A \right\} \right|} \tag{7}$

где $\left\{ A \right\}$ - множество всех значений доли накрытия, $\left\{ S \right\}$ - подмножество $\left\{ A \right\} \ge \beta$ ,- количество повторений процедуры (число статистических испытаний).

Вообще говоря, толерантный интервал не обязательно должен быть центральным, то есть значения толерантных границ $L_{1,2}$ в соотношении (4) могут быть не равны друг другу. На рисунках 5 и 6 приведены два отличных друг от друга интервала, содержащих в себе одну и ту же долю распределения. Квадраты, соответствующие значениям границ, помещены для наглядности на функции плотности:

Рисунок 5 - Доля распределения внутри интервала (-0.68, 1.65)

Рисунок 6 - Доля распределения внутри интервала (-1.65, 0.68)

Уровень доверия

Перейдем к вычислению уровня доверия. Разброс случайной величины удобно измерять в единицах параметра масштаба, в нашем случае - в единицах стандартного отклонения. Проиллюстрируем на примере:

$k_1 = \frac{\hat{\mu}-L_1 }{\hat{s}} \tag{8}$

В нашем случае $L_1 - \hat{\mu}$ - это расстояние от «центра» распределения до одной из толерантных границ, а - соответствующее расстояние в единицах стандартного отклонения. Таким образом, рассчитав уровень доверия к различным значениям доли накрытия для определенных значений коэффициентов мы всегда сможем восстановить границы интервала (соотношение 6) по результатам статистических наблюдений.

Реализуем процедуру расчета, а затем рассмотрим возможные варианты применения толерантных интервалов на практике. Для рабочих задач мне необходима большая статистика и малый шаг вычислительных сеток и $\beta$ , поэтому пришлось реализовывать процедуру на Cи + MPI для запуска на суперкомпьютере. В статье предлагаю использовать Python.

Для начала определим некоторые функции, которые будут нам необходимы.

def cumulative_sum(x):
    """
    Возвращает значение функции вероятности нормального распределения в точке x
    """
    cumulative_sum = (1 + sc.special.erf(x / 2**0.5)) * 0.5
    return cumulative_sum

В модуле stats библиотеки scipy также есть реализации функции вероятности для различных распределений.Теперь непосредственно реализуем процедуру вычисления толерантных границ. Вычисления будем производить для ряда значений коэффициентов .

Зададим два одномерных массива, один из которых содержит значения толерантных коэффициентов , а второй - , например:

k1 = np.linspace(0.05, 10, 100, dtype=np.float64)
k2 = np.copy(k1)

Сгенерируем выборку случайных чисел с нормальным законом распределения размера sample_size. Будем генерировать выборку не один раз, а некоторое число раз num_of_events, равное числу статистических испытаний

# размер выборки n (или число наблюдений)
sample_size = 10
# число статистических испытаний N (сколько раз повторим процедуру)
num_of_events = 10000

Для каждого отдельного повтора по выборке найдем оценки математического ожидания и стандартного отклонения

sample = np.random.randn(sample_size, num_of_events)
sample_means = sample.mean(axis=0)
sample_stds = sample.std(axis=0)

sample_means и sample_stds имеют размерность равную num_of_events, то есть содержат в себе значения среднего и выборочного стандартного отклонения для каждого из num_of_events повторов.

В соответствии с выражением (6) вычислим толерантные границы (также для каждого повтора и каждой пары коэффициентов )

mean_grid, k1_grid, k2_grid = np.meshgrid(sample_means, k1, k2)
std_grid, k1_grid, k2_grid = np.meshgrid(sample_stds, k1, k2)

l1 = mean_grid - k1_grid * std_grid
l2 = mean_grid + k2_grid * std_grid

Рисунок 7 - Расчетная сетка толерантных коэффициентов

Теперь вычислим значения доли накрытия генеральной совокупности каждым толерантным интервалом в соответствии с выражением (4)

stat_coverages = cumulative_sum(l2) - cumulative_sum(l1)

Итоговая функция для расчета доли накрытия в скрытом блоке:

Функция для расчета доли накрытия

def calc_coverages(sample_size, num_of_events, tolerance_factor_lower, tolerance_factor_upper):
    """
    Вычисляет долю накрытия генеральной совокупности с нормальным законом распределения
    толерантными интервалами с заданными границами. Розыгрыш событий производится заданное
    число раз для выборки заданного размера

    Параметры:
        1. sample_size - размер генерируемых выборок из нормального распределения
        2. num_of_events - число статистических испытаний
        3. tolerance_factor_lower - массив нижних толерантных коэффициентов
        4. tolerance_factor_upper - массив верхних толерантных коэффициентов

    Вычисление производится для каждой пары коэффициентов

    Возвращаемые значения:
        1. stat_coverages - статистически вычисленная доля накрытия генеральной совокупности (для каждого испытания)
            толерантным интервалом с коэффициентами tolerance_factor_lower и tolerance_factor_upper
            
            Размерность массива coverages [len(tolerance_factor_lower)][num_of_events][len(tolerance_factor_upper)]
    """

    k1 = tolerance_factor_lower
    k2 = tolerance_factor_upper
    
    sample = np.random.randn(sample_size, num_of_events)
    sample_means = sample.mean(axis=0)
    sample_stds = sample.std(axis=0)
    
    mean_grid, k1_grid, k2_grid = np.meshgrid(sample_means, k1, k2)
    std_grid, k1_grid, k2_grid = np.meshgrid(sample_stds, k1, k2)
    
    l1 = mean_grid - k1_grid * std_grid
    l2 = mean_grid + k2_grid * std_grid
    stat_coverages = cumulative_sum(l2) - cumulative_sum(l1)

    return stat_coverages

Имея рассчитанные значения доли накрытия (4) мы найти число тех, которые не меньше заданного значения required_coverage - $\beta$

required_coverage = 0.95 # Любое значение в интервале [0, 1]
# ось вдоль которой расположены результаты каждого статистического испытания
event_ax = 1
successes = (stat_coverages > required_coverage).sum(axis=events_ax)

Последним шагом, в соответствии с выражением (7) вычислим уровень доверия как отношение числа успехов к общему числу статистических испытаний. Под успехом в нашем случая подразумевается событие, в котором рассчитанная доля накрытия интервалом оказалась не меньше заданной доли

confidence_level = successes / stat_coverages.shape[events_ax]

В результате мы получили зависимость уровня доверия к доле накрытия $\beta$ от толерантных коэффициентов . Повторив данную процедуру для различных значений $\beta$ в диапазоне от 0.01 до 1 получим следующий результат:

Рисунок 8 - Зависимость уровня доверия к доле накрытия от толерантных коэффициентов (для различных значений доли накрытия). Размер выборки

Рисунок 9 - Зависимость уровня доверия к доле накрытия от толерантных коэффициентов (для различных значений доли накрытия). Размер выборки

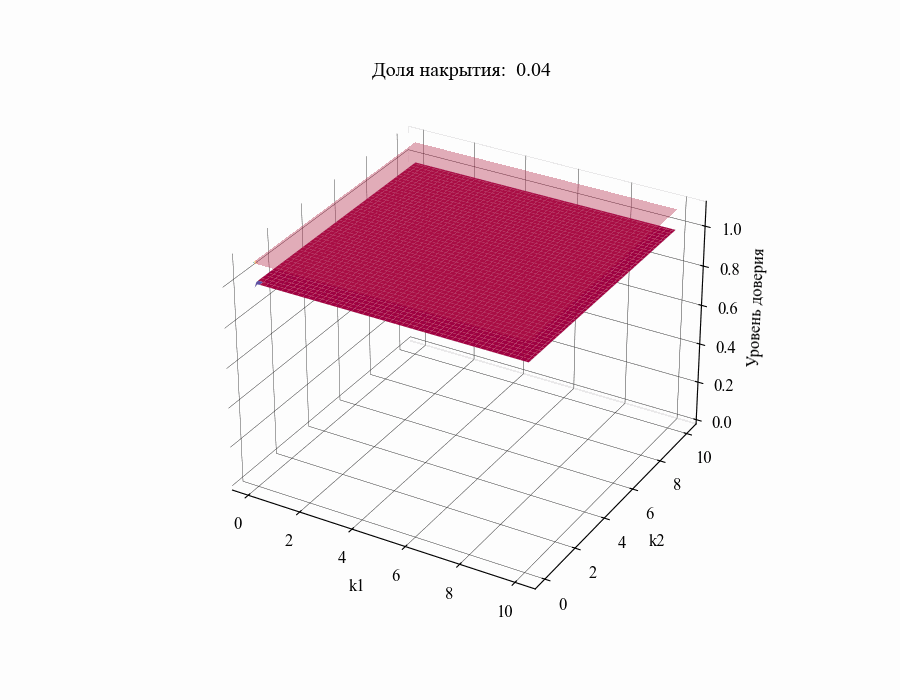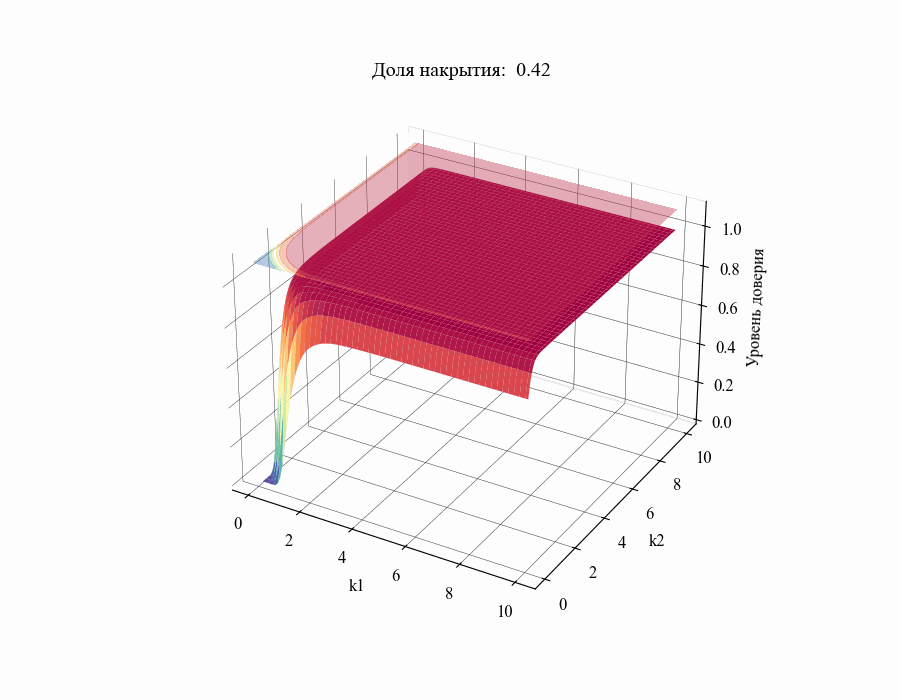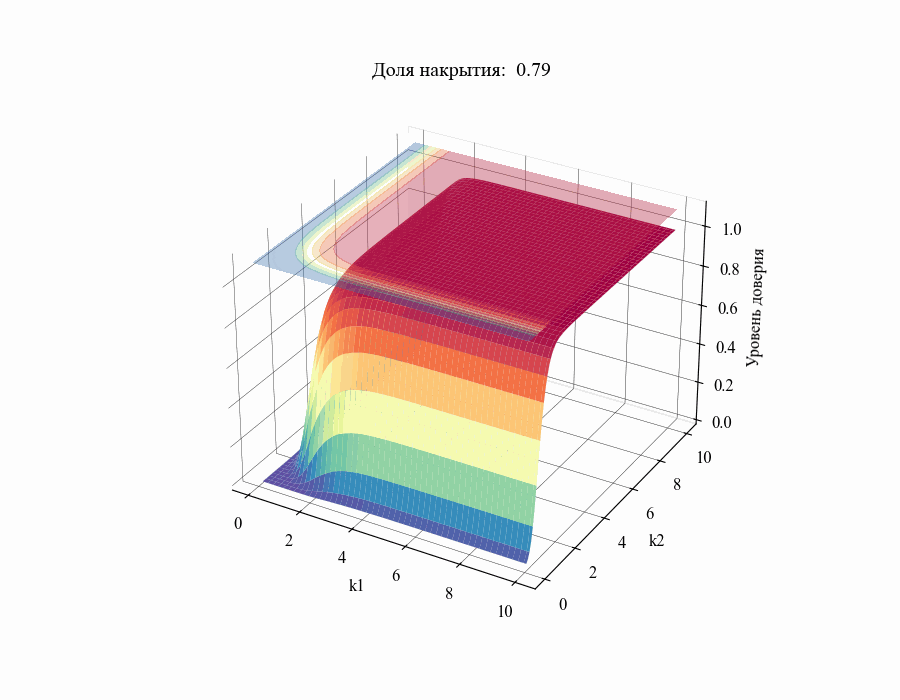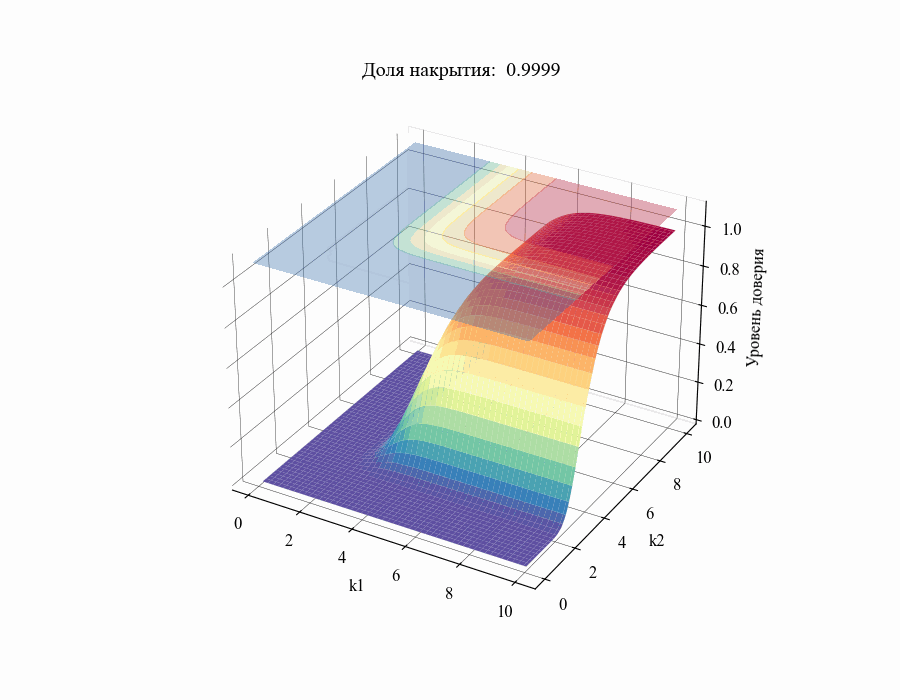
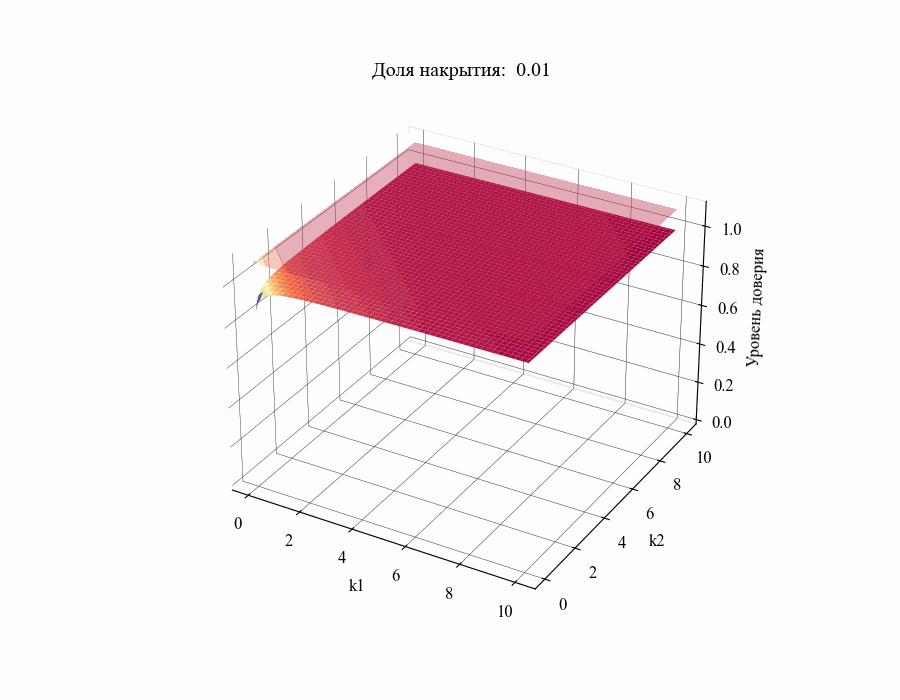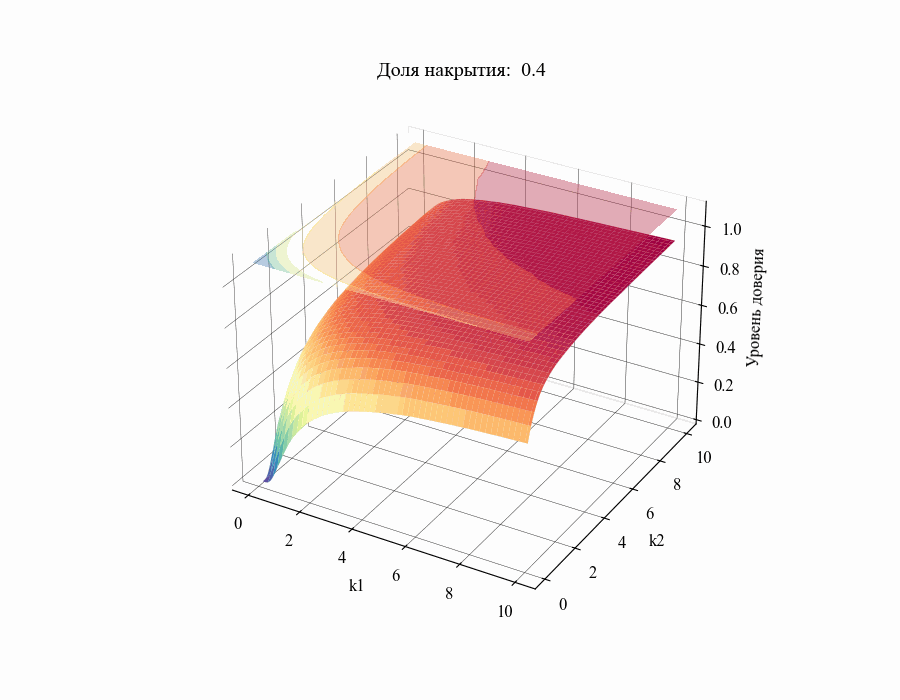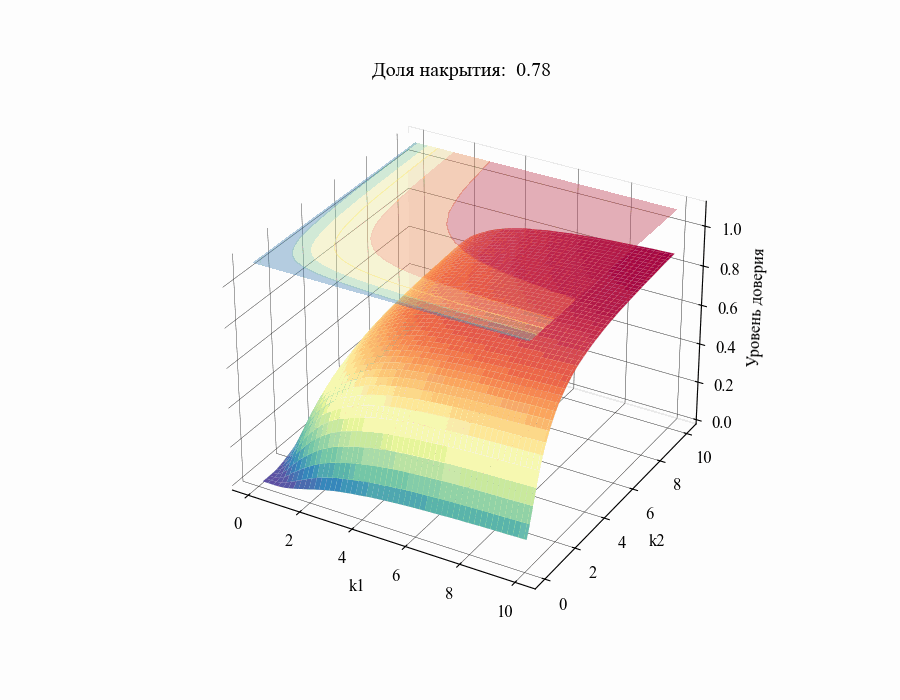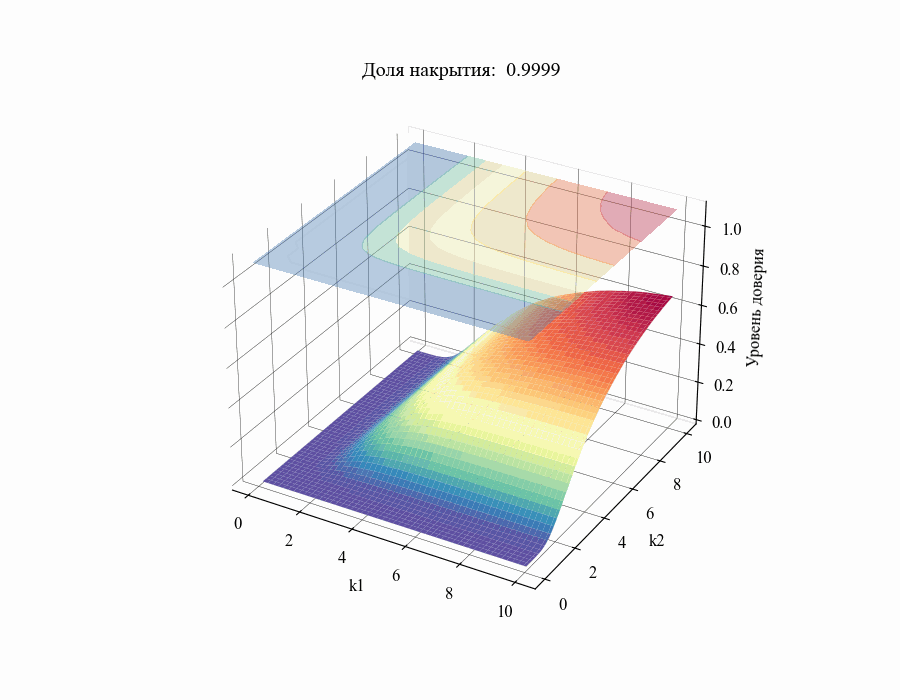
И, например, для различных размеров выборки, на основании которой строится толерантный интервал:

Рисунок 10 - Зависимость уровня доверия к доле накрытия от толерантных коэффициентов (для выборок различных размеров)

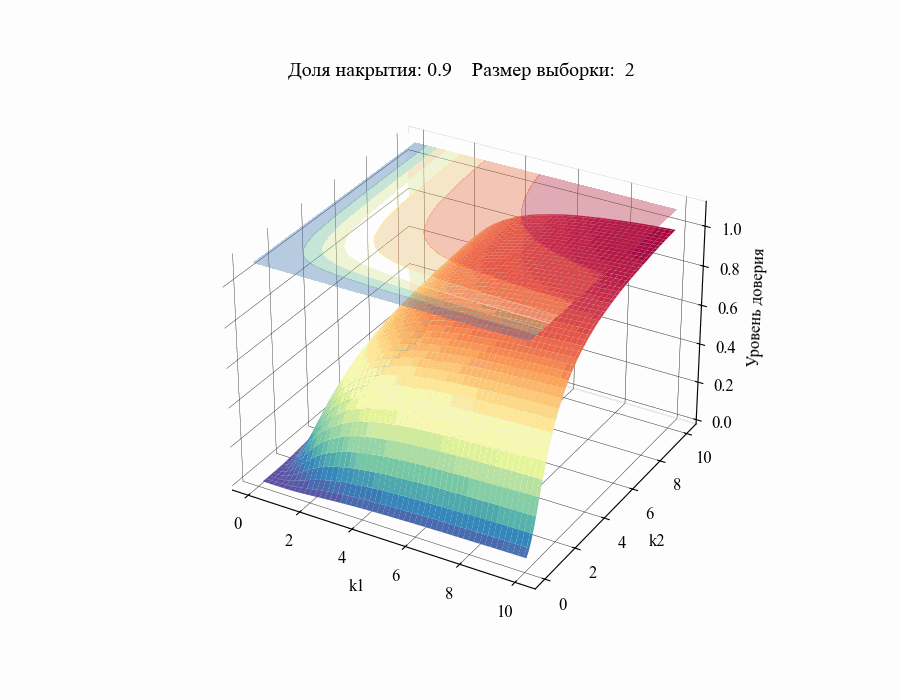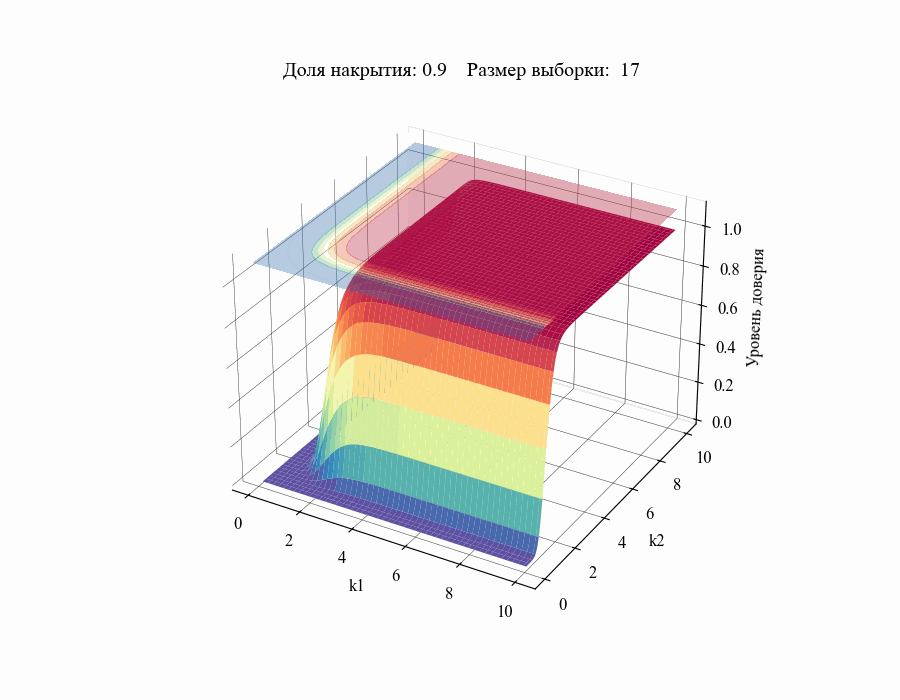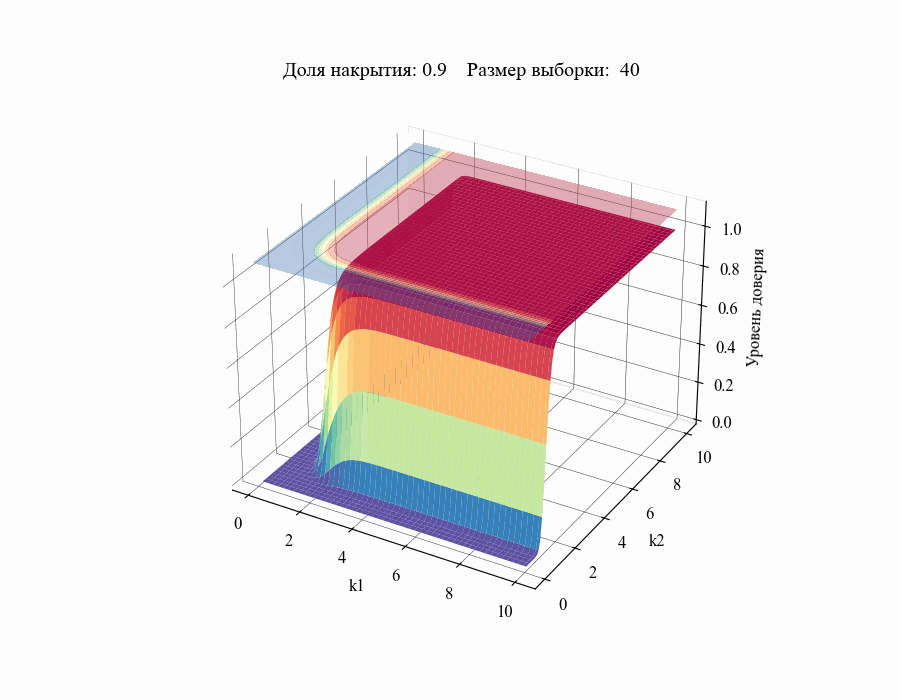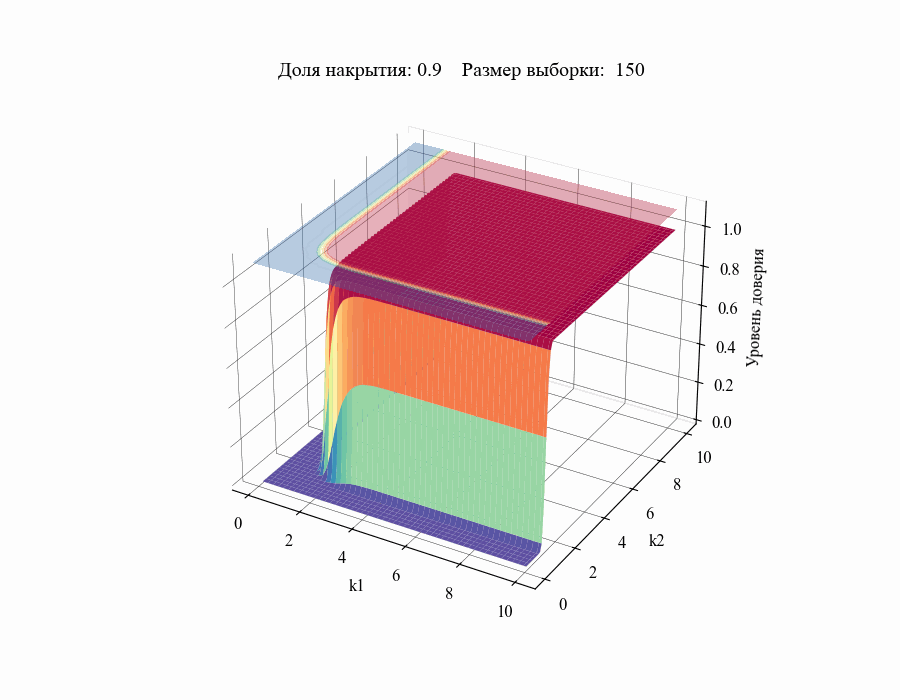
Из полученных зависимостей следуют общие выводы:

Чем о большей части (доле ) генеральной совокупности необходимо сделать утверждение, тем шире должен быть соответствующий толерантный интервал (большие значения толерантных коэффициентов ) для обеспечения одного и того же уровня доверия $\gamma_{const}$ . Еще раз отметим: уровень доверия $\gamma$ - вероятность сделать ложный вывод о доле нашей совокупности;

Для примера - изменение положения точки, соответствующей уровню доверия $\gamma_{const}=0.9$ , при различных значениях доли накрытия:

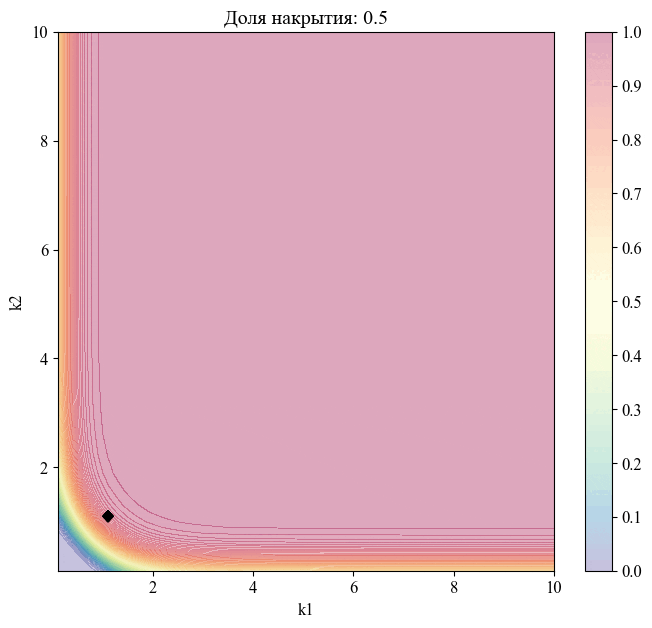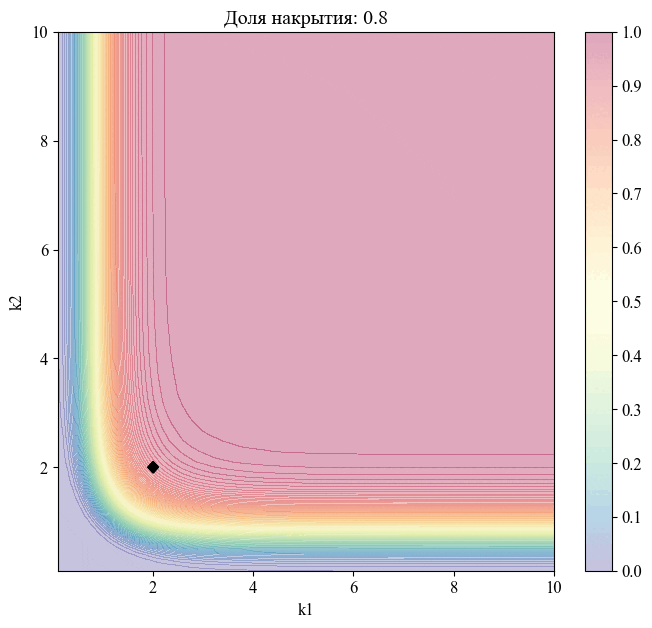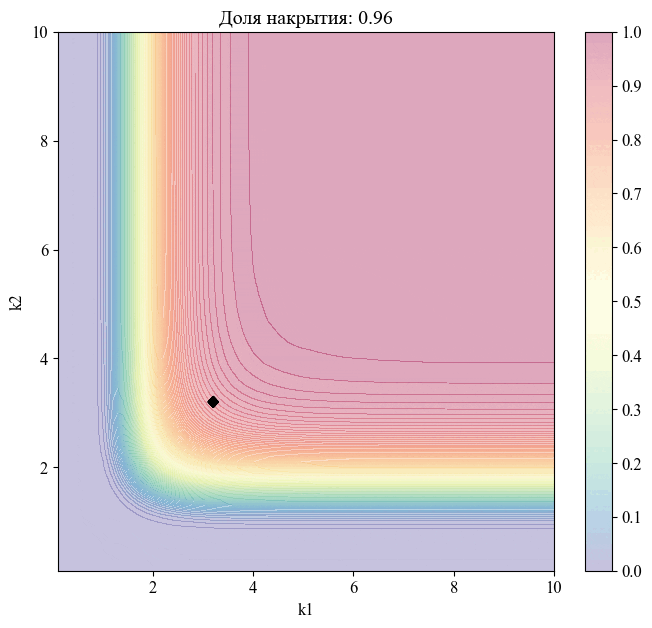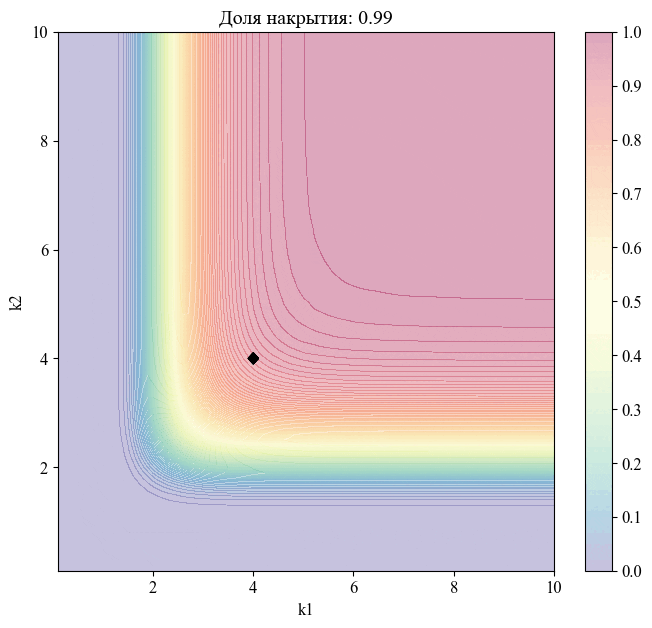
Чем меньше размер выборки, на основании которой мы делаем вывод относительной генеральной совокупности, тем шире границы соответствующего толерантного интервала (рисунок 10).

Обработка результатов наблюдений

Один из возможных вариантов применения - анализ надежности систем различного рода. Для примера, на рисунке 12 приведено изменение тока смещения операционного усилителя [3] от поглощенной дозы:

Рисунок 12 - Ухудшение тока смещения операционного усилителя PM155 в зависимости от дозы

Оригинал:

На рисунке показано ухудшение тока смещения операционного усилителя PM 155 в зависимости от дозы. Было использовано 22 образца из трех различных производственных партий.Среднее значение и граница одностороннего толерантного интервала были рассчитаны для логнормального закона распределения, и $\gamma=0.9$ ^[3]
[3] Christian Poivey. Radiation Hardness Assurance for Space Systems / NASA GSFC, 2002. «Обеспечение радиационной стойкости космических систем».

Смоделируем похожую ситуацию. Пусть необходимо сделать вывод о работоспособности партии (генеральной совокупности) изделий при воздействии определенного фактора, например, ионизирующего излучения космического пространства. Для испытаний на радиационную стойкость из всей партии извлекается выборка размера. В качестве модели, описывающей зависимость значения параметра критерия годности (ПКГ) от воздействующего фактора, выберем модель вида:

$U=a\cdot D \tag{9}$

где - напряжение, являющееся параметром критерия годности; - поглощенная доза излучения; - коэффициент с нормальным законом распределения.

Соответствующий код

loc = 0
scale = 0.01
voltage = lambda a, dose: a * dose

dose = np.linspace(0, 100, 100) # поглощенная доза
lcb = np.zeros_like(dose) - 1 # нижняя критическая граница ПКГ
ucb = np.zeros_like(dose) + 1 # верхняя критическая граница ПКГ

sample_size = 10
voltages = np.empty(shape=(sample_size, dose.shape[0]))

for i in range(sample_size):
    a = sc.stats.norm.rvs(loc=loc, scale=scale)
    voltages[i] = voltage(a, dose)

fig, ax = plt.subplots(figsize=(9, 7))
for v in voltages:
    ax.plot(dose, v, lw=0.7)
    
average = voltages.mean(axis=0)
ax.plot(dose, lcb, lw=2, c='#00FF00', label='Критическое значение ПКГ')
ax.plot(dose, ucb, lw=2, c='#00FF00')
ax.plot(dose, average, lw=3, c='b', label='Среднее значение ПКГ')

Результат приведен на рисунке 13:

Рисунок 13 - Зависимость напряжения от поглощенной дозы излучения

Зелеными линиями на рисунке обозначены верхняя и нижняя критическая граница параметра критерия годности, то есть значение напряжения, при достижении которого изделие считается вышедшим из строя (временная потеря работоспособности, необратимый отказ и так далее).

С помощью толерантных интервалов по результатам испытаний определим с % ошибкой вероятность сохранения работоспособности при соответствующем уровне воздействия. То есть, для каждого значения дозы мы будем искать долю всех изделий для которой можно сделать вывод о нахождении ПКГ внутри интервала $(U_{крит. мин.}, U_{крит. макс.})$ с уровнем доверия $\gamma = (100-5)$ %.

Выполним следующие действия:

Для каждого значения уровня воздействия по результатам испытаний найдем толерантные коэффициенты

Рисунок 14 - Пара толерантных коэффициентов для значения

Для каждой пары коэффициентов найдем значение (рисунок 8), для которого выполняется условие:

$\left|\gamma (P, k_1,k_2)-0.95 \right| \longrightarrow min \tag{10}$

Итоговая функция для обработки результатов

def search_nearest(array, target):
    return np.argmin(np.abs(array - target))

  
def get_coverages(confidence_arr, coverages_mesh, required_confidence, voltages, lcb, ucb, tolerance_mesh):
    """
    Возвращает значение доли накрытия P, для которого уровень доверия максимально близок к заданному

    Параметры:
        1. confidence_arr - трехмерный массив значений уровня доверия, где первая ось соответствует
        каждому значению доли накрытия; вторая и третья - толерантным коэффициентам k1 и k2
        2. coverages_mesh - одномерный массив значений доли накрытия, для которых расчитан confidence_arr
        3. required_confidence - требуемый уровень доверия к результату
        4. voltages - массив, содержащий результаты испытаний (зависимости напряжения от дозы)
        5. lcb - нижняя граница параметра критерия годности (массив)
        6. ucb - верхняя граница параметра критерия годности (массив)
        7. tolerance_mesh - одномерный массив значений толерантных коэффициентов (узлы расчетной сетки)

    Возвращаемое значение:
        1. coverages - массив значений доли накрытия (для каждого значения уровня воздействия),
        для которых уровень доверия равен требуемому required_confidence
    """
    
    mean = voltages.mean(axis=0)
    std = voltages.std(axis=0)
    k1_exp = (mean - lcb) / std
    k2_exp = (ucb - mean) / std
    k1_indices = np.array([search_nearest(tolerance_mesh, k) for k in k1_exp])
    k2_indices = np.array([search_nearest(tolerance_mesh, k) for k in k2_exp])

    coverages = np.empty_like(mean)

    for i in range(k1_indices.shape[0]):
        distance_init = 1e6
        
        for j, arr in enumerate(confidence_arr):
            confidence_level = arr[k1_indices[i]][k2_indices[i]]
            distance = np.abs(confidence_level - required_confidence)

            if distance <= distance_init:
                distance_init = distance
                coverages[i] = coverages_mesh[j]

    return coverages

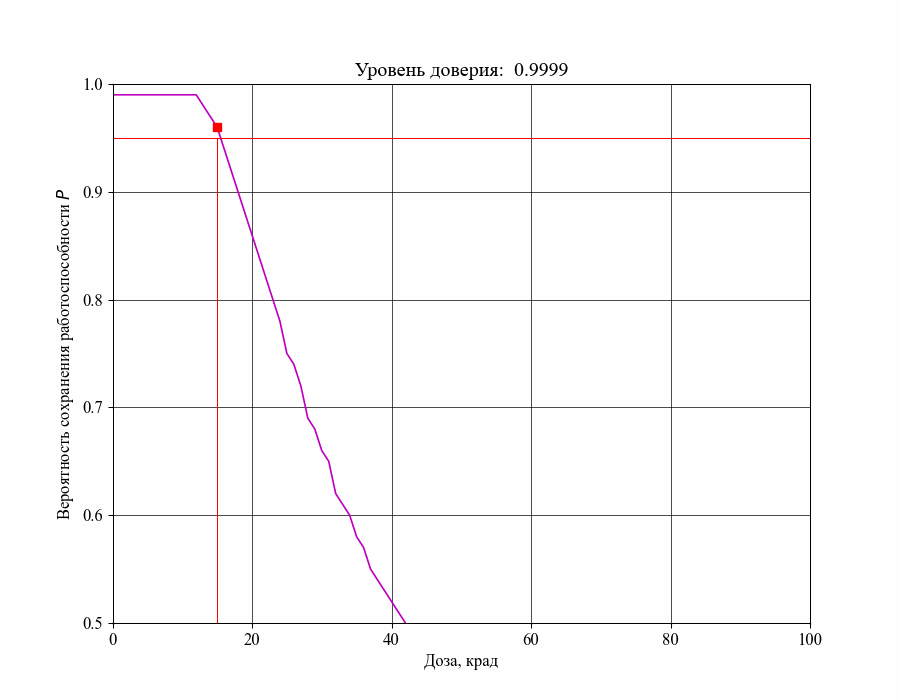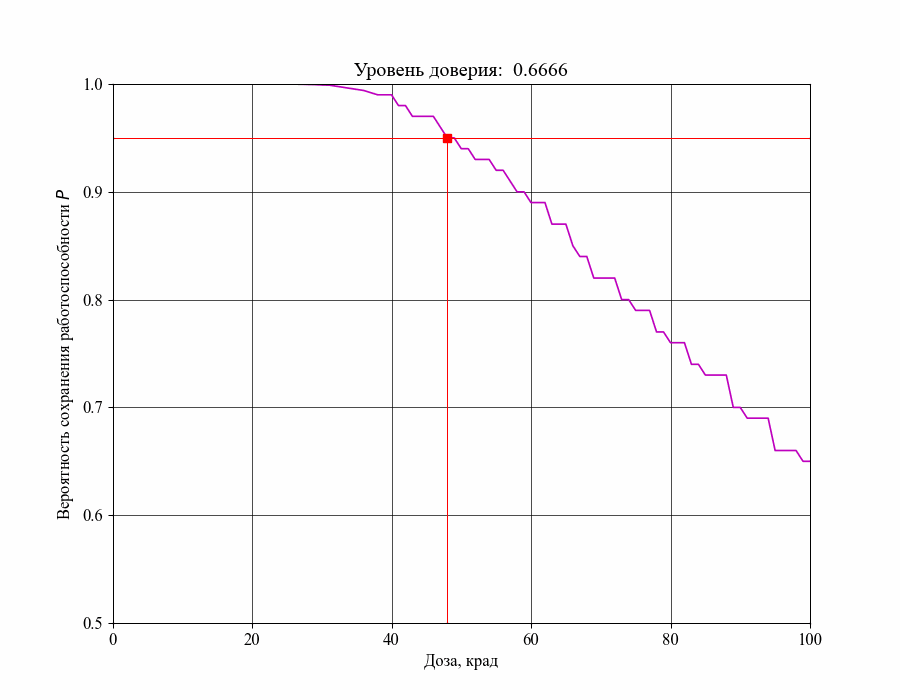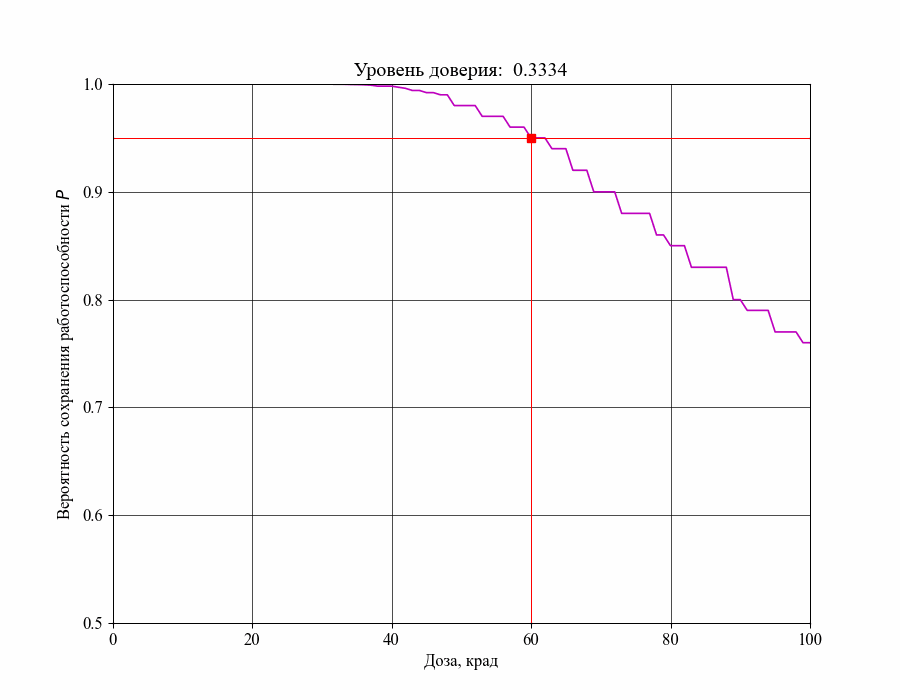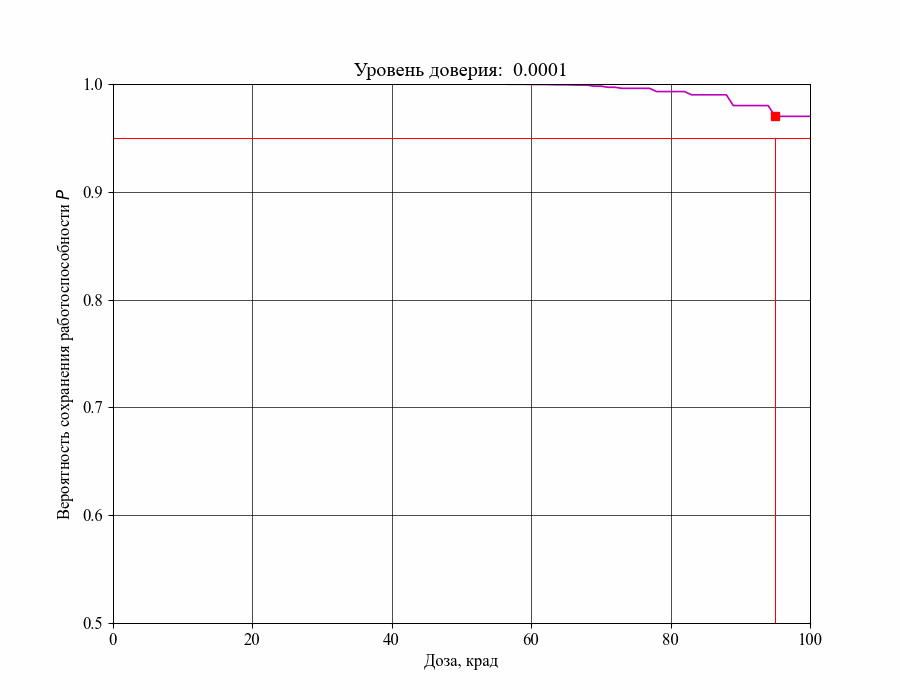
В результате получаем зависимость следующего вида:

Рисунок 15 - Зависимость вероятности сохранения работоспособности (доля генеральной совокупности, которая с заданным доверием находится внутри интервала) от уровня воздействия — Рисунок 15 - Зависимость вероятности сохранения работоспособности (доля генеральной совокупности, которая с заданным доверием $\gamma=0.95$ находится внутри интервала) от уровня воздействия

Выбрав, например, максимально допустимую вероятность отказа % можем получить оценку критического уровня воздействия - максимальную поглощенную дозу излучения, которую в данном случае нельзя превышать для выполнения требования:

Рисунок 16 - Изменение критической границы для уровня воздействия в зависимости от требований

Заключение

В заключение хотелось бы сказать, что, конечно, область возможного применения толерантных интервалов не ограничивается одной лишь теорией надежности, и приведенный пример использования далеко не единственный, а просто один из многих. Как мне кажется, в принципе, данная идея может быть использована в любой области, затрагивающей вопросы статистической обработки данных. Например, возможно также осуществление обработки (корректировки поведения каких-либо систем на основе поступающих данных) не только в статике, но и в динамике и многое другого.

Мы рассмотрели только случай нормального распределения, но общая концепция может быть распространена и на другие законы распределения, в том числе и распределение Коши. В таком случае, необходимо будет выбрать соответствующие методы построения оценок параметров сдвига и масштаба. Также существуют методы построения так называемых «свободных от закона распределения» толерантных интервалов; подробнее можно почитать в книге:

[4] Кендалл М., Стюарт А. Статистические выводы и связи. М., Наука, Физматлит, Т. 2, 1973. — 899 с.

Вообще, все три тома хорошие, особенно могут быть полезны тем, кто занимается теоретической статистикой.

На этом, наверное, все. В данной статье я постарался поделиться с вами личным опытом знакомства с толерантными интервалами и понагляднее описать некоторые моменты, надеюсь, что кому-то приведенная информация сможет оказаться полезной. Буду рад вашему мнению, замечаниям или критике. Всем желаю здоровья и творческих успехов. Спасибо.

Теги:

Хабы:

Обработка результатов статистических наблюдений с помощью толерантных интервалов

Толерантные интервалы

Уровень доверия

Обработка результатов наблюдений

Заключение

Публикации

Работа

Ближайшие события