
Несколько лет назад я работал над проектом по реализации на Unity реалистичного космического симулятора. Это достаточно нестандартное применение движка, и в ходе работы были решены разные специфические задачи, одна из которых - обеспечение корректного рендеринга объектов космических масштабов. Этим опытом я бы хотел поделиться с сообществом.
Тема космоса достаточно популярна в компьютерных играх, но обычно представлена лишь сеттингом, декорацией или статичным задним фоном для происходящего на переднем плане. Реалистичный космос, подразумевающий огромные размеры объектов и колоссальные расстояния между ними встречается не так часто - обычно в достаточно нишевых продуктах типа игры Kerbal Space Program или в интерактивных планетариях, как SpaceEngine. На мой взгляд, у этого есть две основные причины. Во-первых реалистичный космос сложно вписать в динамичный геймплей, а во-вторых он имеет определенные технические сложности в реализации. Оставлю первый вопрос геймдизайнерам и попробую рассказать о технической стороне вопроса, а конкретно - о проблемах рендеринга в таких проектах.
Ценз опыта: для понимания приведенных в статье решений не потребуется глубинных знаний об устройстве процесса рендеринга или высшей математики. Достаточно базово понимать что такое камера в Unity, и знать алгебру и геометрию на уровне 9 класса школы

В тексте этой статьи встречаются очень длинные числа и чтобы не возникло путаницы, запятые будут используются для отделения разрядов числа, а точка для отделения целой части от дробной. Пример:
15,478.05- пятнадцать тысяч четыреста семьдесят восемь целых и пять сотых
Постановка задачи
Требования к реализации реалистичного космического пространства могут значительно отличаться в зависимости от специфики проекта. Чтобы упростить повествование, я придумаю сам себе техническое задание и покажу решение в его рамках.
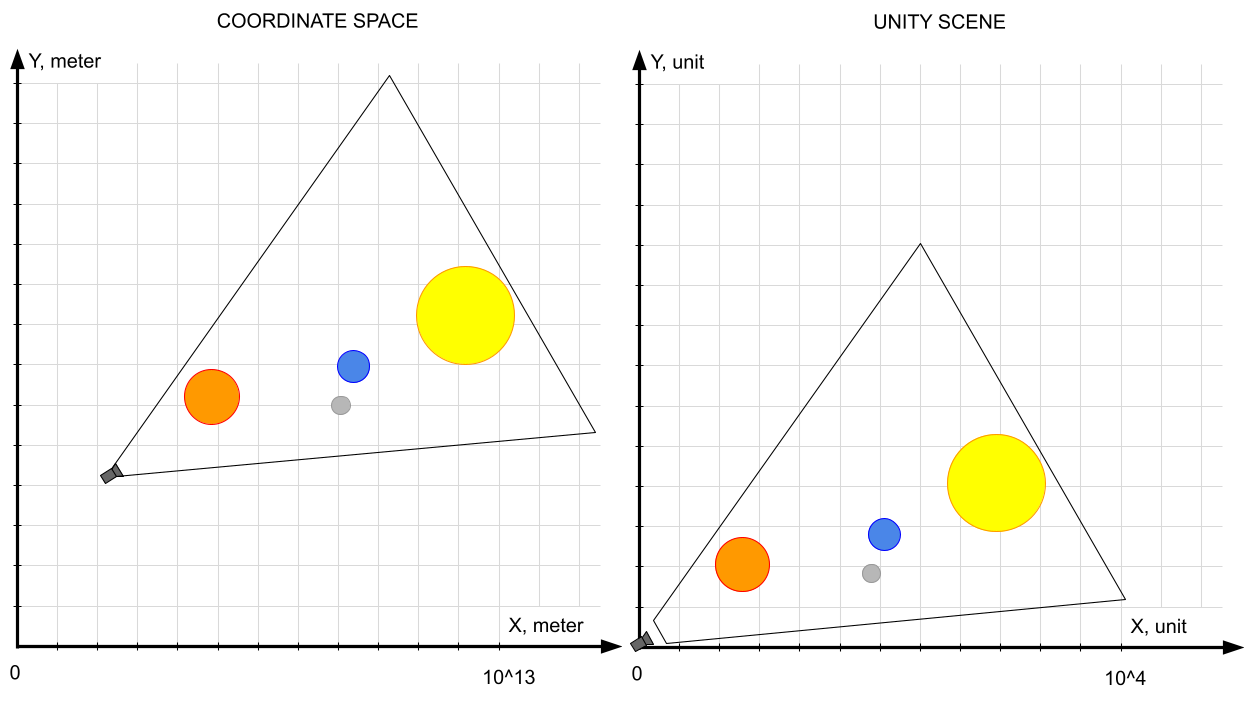
Итак, допустим требуется реализовать в на движке Unity упрощенную визуальную модель солнечной системы, соответствующую следующим критериям:
В ней должны быть представлены космические объекты, причем весьма различающихся размеров:
Звезда по имени Солнце - радиус
696,340кмПланеты и некоторые спутники, например Земля - радиус
6,371км и Луна - радиус1,737кмИскусственный спутник, размах
крыльевсолнечных панелей - несколько метров
Помимо реальных объектов должны присутствовать инфографики - плоскость эклиптики и линии обозначающие высоту реальных объектов над ней
Объекты и камера в общем случае не статичны, могут быть быть расположены где угодно в пределах пространства и иметь произвольный поворот. Для тестирования будет реализован орбитальный режим камеры
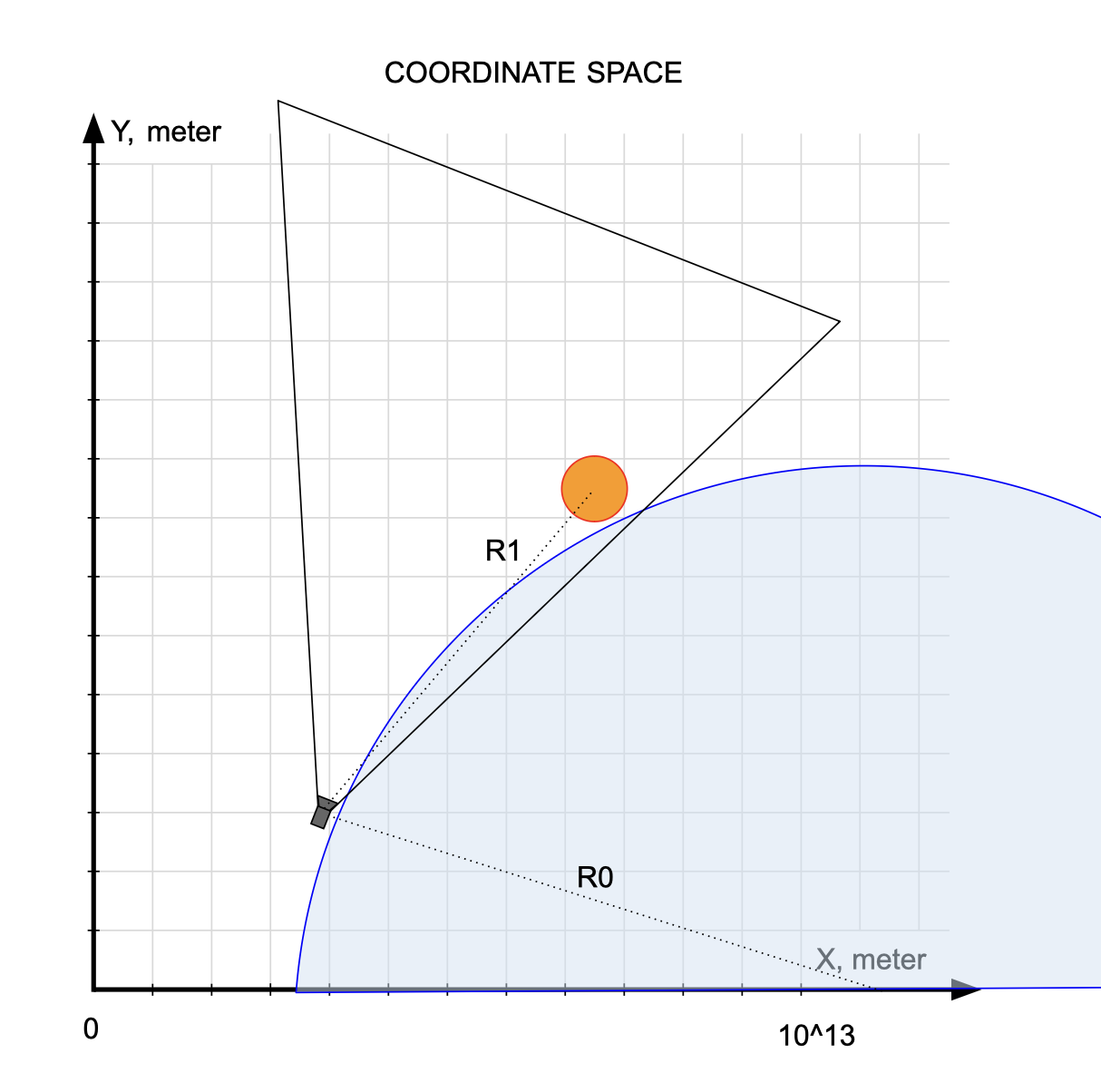
Пространство условно ограничено радиусом орбиты Плутона
Под “системой рендеринга” я понимаю совокупность логики, которая обеспечивает выполнение следующих условий:
Объекты в итоговом кадре должны иметь такие же размеры и соотношения сторон, какие они имели бы на реальной камере с такими же параметрами
Объекты не должны дрожать и обрезаться ни при каких условиях (за исключением ситуации, когда камера попала внутрь объекта - в этом случае его нужно просто скрыть)
В рамках этой статьи будут рассматриваться только вопросы построения системы рендеринга, и за бортом останутся многие другие темы, такие как:
Физика космических объектов, гравитационное взаимодействие, расчет координат объектов - я просто возьму дальность планет от солнца из таблицы и выстрою их в ряд. Так же будет реализован альтернативный режим, где объекты выставлены близко друг к другу, чтобы было легче сравнивать их размеры
Кастомный рейкаст для выбора объектов в сцене по клику
Система освещения и реалистичные тени - свет будет статичен а тени просто отключены
Проблема точности чисел с плавающей точкой
Для начала нужно выяснить, а в чем собственно заключается проблема? Разве нельзя просто создать сферы в сцене Unity, накинуть на них текстуры планет и задать им нужные координаты и масштаб?

Сразу возникает вопрос о преобразовании координат - как размеры и позиции объектов в метрах превратить в юниты (единицы измерения в Unity)? Введем понятие коэффициента преобразования MeterToUnit. По сути это коэффициент масштаба всего пространства, который применяется и к координатам объектов и к их размерам. Соответственно при MeterToUnit = 1 мы и получаем соотношение 1 метр = 1 юнит. Попробуем поработать с таким коэффициентом. Примем за начало координат центр Солнца и попробуем задать планетам в сцене позиции и размеры, но замечаем что мы дошли только до Марса, а ему уже поплохело - сфера слегка деформировалась а Unity выдает какое-то предупреждение.
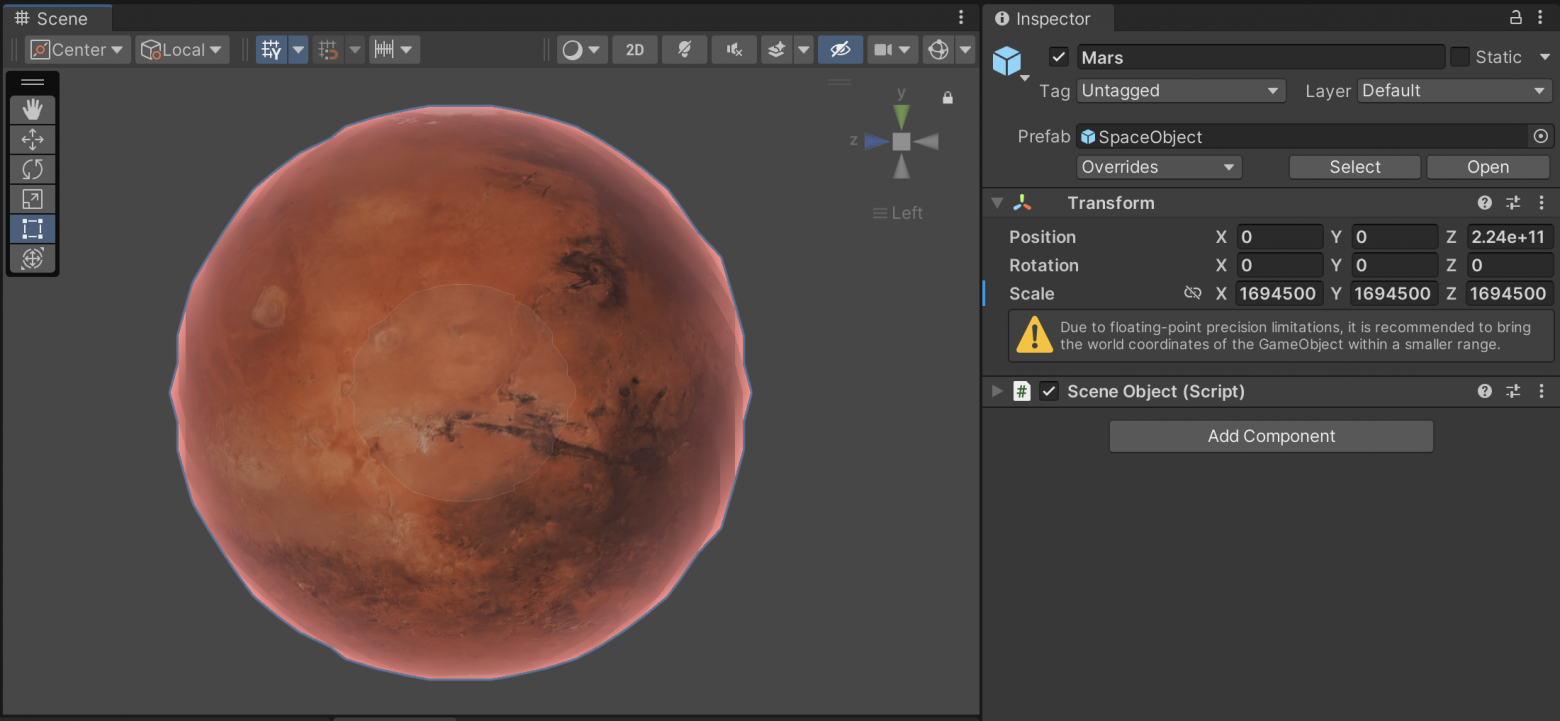
Position и Scale слишком велики - Unity рычитПричина этой проблемы - недостаточная точность float для хранения настолько длинных чисел (причем именно длинных, а не просто больших). Ведь во float можно сохранить как большие числа например 1,000,000, так и очень маленькие, например 0.000,001, но не их сумму 1,000,000.000,001, потому что в нем, как и в других типах данных с плавающей точкой, сохраняются только N первых цифр числа (его старших разрядов), а остальные просто теряются. Количество сохраняемых чисел зависит от точности типа, для float сохраняются примерно 7 десятичных разрядов а для double примерно 16.
Более подробное описание проблемы точности чисел с плавающей точкой
Давайте временно забудем о сцене в Unity и поговорим только о том, как мы собираемся хранить в коде координаты космических объектов. Представим что мы хотим показать полет небольшого космического аппарата к Плутону - самому удаленному от Солнца, объекту в нашем проекте. Максимальное расстояние от Солнца до Плутона составляет примерно 7,375,930,000,000 метров и нам нужен тип данных, способный корректно хранить числа такого порядка. Почему я привел расстояние именно в метрах, а не например в астрономических единицах? Потому что я выбрал единицу измерения, которая соответствует характерному размеру наименьшего объекта - космического аппарата, ведь чтобы его движение было плавным а не скачкообразным, нужно чтобы шаг сетки координат составлял хотя бы одну сотую от его размера т.е. примерно 0.01 метра или 1 сантиметр, а значит помимо старших разрядов точности типа должно хватать так же минимум на два разряда после запятой.
Справятся ли float и double, стандартные типы данных с плавающей точкой отличающиеся точностью, с такими числами? Проведем эксперимент, попробуем записать в переменные типа float и double значения взятые из числа, записанного в строке:
void Start() { var textValue = "7,375,931,234,567.8912"; float a = float.Parse(textValue); double b = double.Parse(textValue); Debug.Log(a.ToString("N5")); // Output: 7,375,931,000,000.00000 Debug.Log(b.ToString("N5")); // Output: 7,375,931,234,567.89000 }
Как мы видим, значения выведенные в консоль не соответствуют исходной строке, переменная float обрезала очень много разрядов, тогда как переменная double потеряла только две цифры на конце, но в целом в норматив уложилась.
Так почему же цифры потерялись? Чтобы ответить на этот вопрос, напомню как устроены числа с плавающей точкой, а конкретно - что такое экспоненциальная форма представления вещественных чисел, которая используется в их реализации. Например число 1.2345 в экспоненицаильной форме и десятичной системе счисления представляется как 12345 * 10^-4и концептуально состоит из четырех отдельных частей, а именно:
Мантиссы - первых N цифр для старших разрядов числа, в данном случае
12345Порядка - степени над десяткой, в данном случае
4Знака мантиссы, в данном случае
+Знака порядка, в данном случае
-
Хотя это максимально упрощенное описание, не учитывающее некоторую специфику их реализации (и в частности перевод из десятичной системы в двоичную), этого достаточно для понимания нашей проблемы. А в нашем случае проблема очевидно в том, что для длинных чисел длины мантиссы может не хватить. Например, если бы мантисса хранила только три десятичных знака, то от исходного числа 1.2345 в такую переменную можно было бы записать только 1.23. Таким образом, чем больше в числе цифр до запятой, тем меньше сохранится цифр после нее. Именно из-за этого в приведенном выше примере кода у float точность исходного числа 7,375,931,234,567.8912 потерялась уже на шестом знаке до запятой а у double хватило на два разряда после нее.
Дополнительный пример
Для закрепления понимания проблемы, приведу еще один пример, как переменной типа float уже не хватает точности даже для инкремента (сложения с единицей), но для double длины мантиссы еще достаточно для правильного расчета. В то же время, если заменить цикл на прямое сложение с сотней, то результат для обоих типов будет верный. Если вы понимаете как это работает, то вы готовы к собеседованию в гугл мы можем двигаться дальше.
void Start() { var textValue = "100,000,000"; float a = float.Parse(textValue); double b = double.Parse(textValue); for (int i = 0; i < 100; i++) { a++; b++; } //a += 100f; //b += 100d; Debug.Log(a.ToString("N2")); // Output: 100,000,000.00 Debug.Log(b.ToString("N2")); // Output: 100,000,100.00 }
Так почему же сфера в сцене Unity деформировалась? Потому что в процессе рендеринга во float рассчитываются абсолютные координаты всех вершин сферы в сцене, и чем дальше сфера удалена от центра, тем больше разрядов координат вершин тратится на хранение их сдвига от центра, и тем меньше разрядов остается на хранение расстояния между самим вершинами. Очевидно это так же зависит от параметра Scale - масштаба сферы. Чем он больше, тем более удалены друг от друга ее вершины, и соответственно большие сферы при удалении от центра будут ломаться медленнее чем маленькие. Вы можете легко воспроизвести этот опыт самостоятельно, поместив любую модель в сцену Unity и наблюдать ее деформации при сдвиге от центра координат.
И хотя для расчетов координат объектов внутри кода мы можем использовать тип double, точности которого для наших целей достаточно, при заполнении полей компонента Transform произойдет приведение к типу float и точность потеряется. Эта ограничение не только компонента Transform или даже движка Unity, а скорее исторически сложившееся требование со стороны GPU продиктованное вопросом производительности.
Насколько мне известно, double-precision координаты для объектов сцены сейчас поддерживается в Unreal Engine 5 и в Unigine, и возможно будет правильным решением использовать для таких проектов именно эти движки. Тем не менее, когда я несколько лет назад работал над этой задачей, такие возможности еще не были доступны в движках “из коробки”, и я разработал решение в рамках Unity, о этапах реализации которого расскажу далее.
Подготовка проекта
Чтобы сократить объем текста я решил не вставлять в него примеры кода а лишь тезисно объяснять принципы работы предложенных алгоритмов. К данной статье прилагается Unity-проект с исходным кодом а так же WebGL билд. Ссылки расположены в конце статьи
Приступим непосредственно к реализации нашего проекта. Итак, у нас имеются различные космические объекты (Солнце, планеты, инфографики, искусственный спутник), реальные размеры которых нам известны. Но если планеты можно условно считать сферическими и характеризовать их только радиусом, то как поступить например с искусственным спутником, который имеет сложную форму?

Очень просто - засунем его внутрь невидимого сферического контейнера так, чтобы он полностью туда помещался. Так же поступим и для других объектов не-сферической формы. Важно понимать, что под сферическим контейнером я понимаю исключительно математическую условность - тот факт, что для каждого объекта определены координаты и радиус и то как мы их обрабатываем, а не коллайдер или меш в сцене Unity.
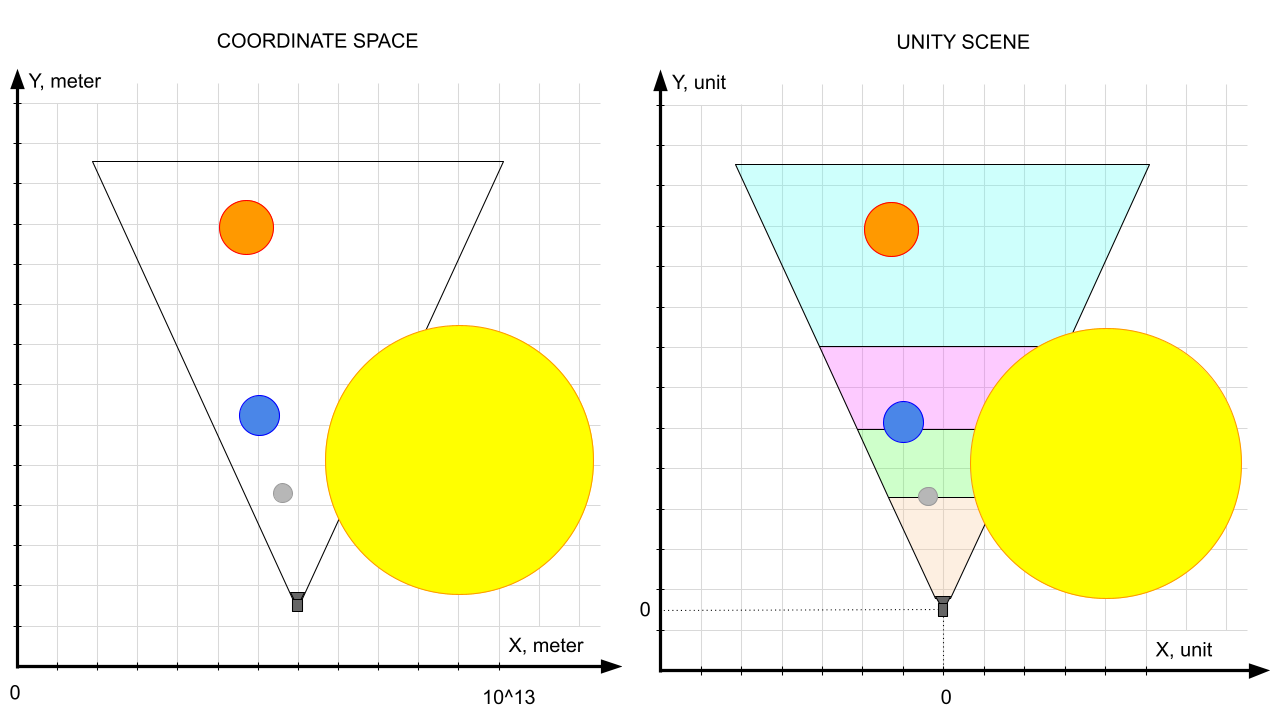
По сути у нас будет будет два “мира“:
“Мир координат”, который состоит из:
Массива данных всех космических объектов, для каждого из которого определены:
Координаты центра сферы относительно центра Солнца в метрах. В предыдущем разделе мы установили что для хранения координат нам подойдет тип
double, но так как координат три, то будем использовать double-версию вектора -Vector3dРадиус описывающей объект сферы в метрах,
doubleЛокальный поворот объекта,
Quaternion. Как известно, это матрица со значениями типаfloat, но для поворота проблема с точностью не так актуальна, поэтому мы не будем заменять его на double-версиюФлаг
Solid,bool- указывает на то, является ли объект “твердым”. Для реальных объектов онtrueа для инфографикfalse
Камеры, для которой определены:
Координаты,
Vector3dПоворот,
QuaternionДля камеры в мире координат нет понятия “плоскость клипирования” - это просто точка и направление обзора. В идеале мы должны видеть все объекты в области видимости, а дальность ограничивается только размерами пространства
“Мир сцены Unity” содержит:
GameObject’ы, которые отвечают за визуальное представление наших космических объектов и инфографикКамеру в сцене, которая помимо позиции и поворота содержит много других параметров
Задача системы рендеринга - быть посредником между этими мирами. “Мир координат” для нее представляет входные данные (они рассчитываются другими системами), на основе которых она должна сконфигурировать “Мир сцены Unity”, т.е. расставить объекты по сцене и настроить камеру так, чтобы обеспечить коррект��ый рендеринг.

Очевидно, что поворот сферических объектов (но не камеры) вокруг собственной оси не меняет структуру сцены, поэтому забегая вперед скажу, что
Rotationобъектов от “мира координат” во всех приведенных ниже методах напрямую, без всяких изменений, переходит в “мир сцены Unity”, поэтому для лаконичности текста этот шаг не будет упоминаться в описании алгоритмов
Решение в лоб. Метод простого масштабирования
Как уже было сказано, слишком большие числа координат объектов являются первой (но не единственной) проблемой, с которой мы сталкиваемся. Можем ли мы решить ее, просто применив ко всем расстояниям и размерам понижающий множитель, т.е. сделав коэффициент MeterToUnit сильно меньше единицы?
Логика работы такой системы рендеринга будет максимально проста:
Исходные координаты объектов и камеры умножаются на коэффициент
MeterToUnitи присваиваются позициям соответствующих объектов в сценеРазмеры объектов умножаются на
MeterToUnitи присваиваются масштабам объектов
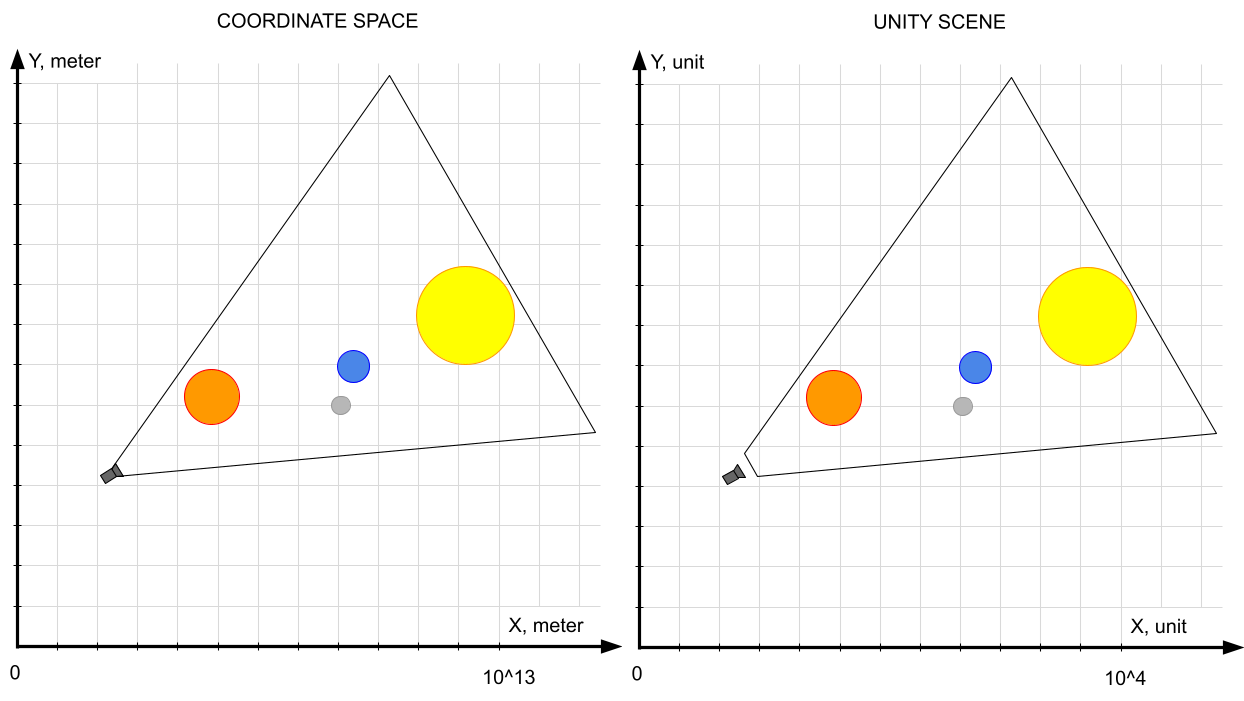
(видно по изменению порядков на шкале)
Решит ли такая система наши задачи? Короткий ответ - нет. Этот результат очевиден с точки зрения устройства чисел с плавающей точкой- простым умножением числа на некий множитель проблему не решить - будет сдвигаться лишь порядок числа, но проблема недостатка длины мантиссы не решится.
Если MeterToUnit не достаточно мал, то координаты объектов (особенно дальних) выйдут за границы точности float и маленькие объекты будут трястись.
Далее на скриншотах из редактора вы будете видеть скрипт
SceneObject, который предназначен для хранения параметров объекта от “мира координат”, а в полях компонентаTransform(PositionиScale) - значения, рассчитанные системой рендеринга. Следует отметить, чтоScaleобъекта соответствует диаметру сферы, а вSceneObjectзаписан радиус объекта, который помимо прочего нужно умножать на 2.Rotationже вSceneObjectфактически не реализован, но если бы он и был то присваивался бы объекту в сцене без изменений
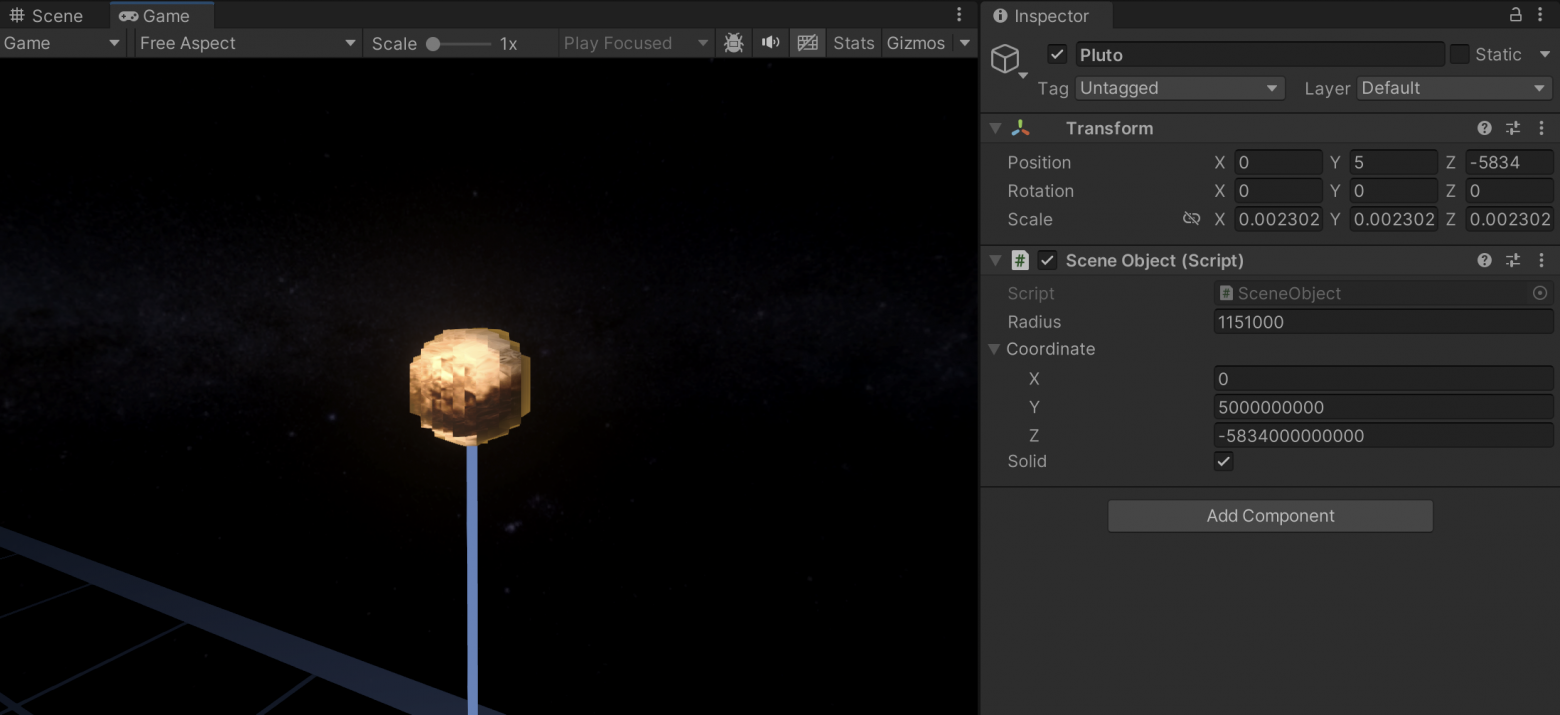
MeterToUnit = 1E-09, Position слишком велик а Scale мал - Плутон попердолелоЕсли же MeterToUnit слишком мал, то объекты будут обрезаться ближней плоскостью клипирования камеры. Поясню этот момент подробнее. Чтобы рассмотреть космический объект с близкого расстояния, нам нужно придвинуть к нему камеру почти в упор, но мы натыкаемся на то, что расстояние до ближней плоскости клипирования (NearClip) для камеры с перспективной проекцией не может быть установлено меньше чем 0.01 юнита.
Зная это, мы можем рассчитать минимально возможную дальность до объекта в метрах: 0.01f / MeterToUnit. В тестовом проекте, логика орбитальной камеры работает так, что минимальное расстояние от центра объекта до камеры пропорционально его радиусу, и если для крупных объектов расстояния до камеры при максимальном зуме будет достаточно, то для меньших объектов - нет.

Выводы
Метод предельно прост в реализации
В нашем случае результат неудовлетворительный, возникают неразрешимые проблемы с маленькими и дальними объектами
Нельзя подобрать параметр
MeterToUnitчтобы все объекты отображались корректно - объекты обрезаются или дрожат (иногда и то и другое одновременно)Метод вполне подходил бы, если бы все объекты были размером с Солнце, потому что тогда, даже на максимальном удалении от центра координат, их
Scaleбыл бы достаточно большим и они бы не тряслись и не обрезались
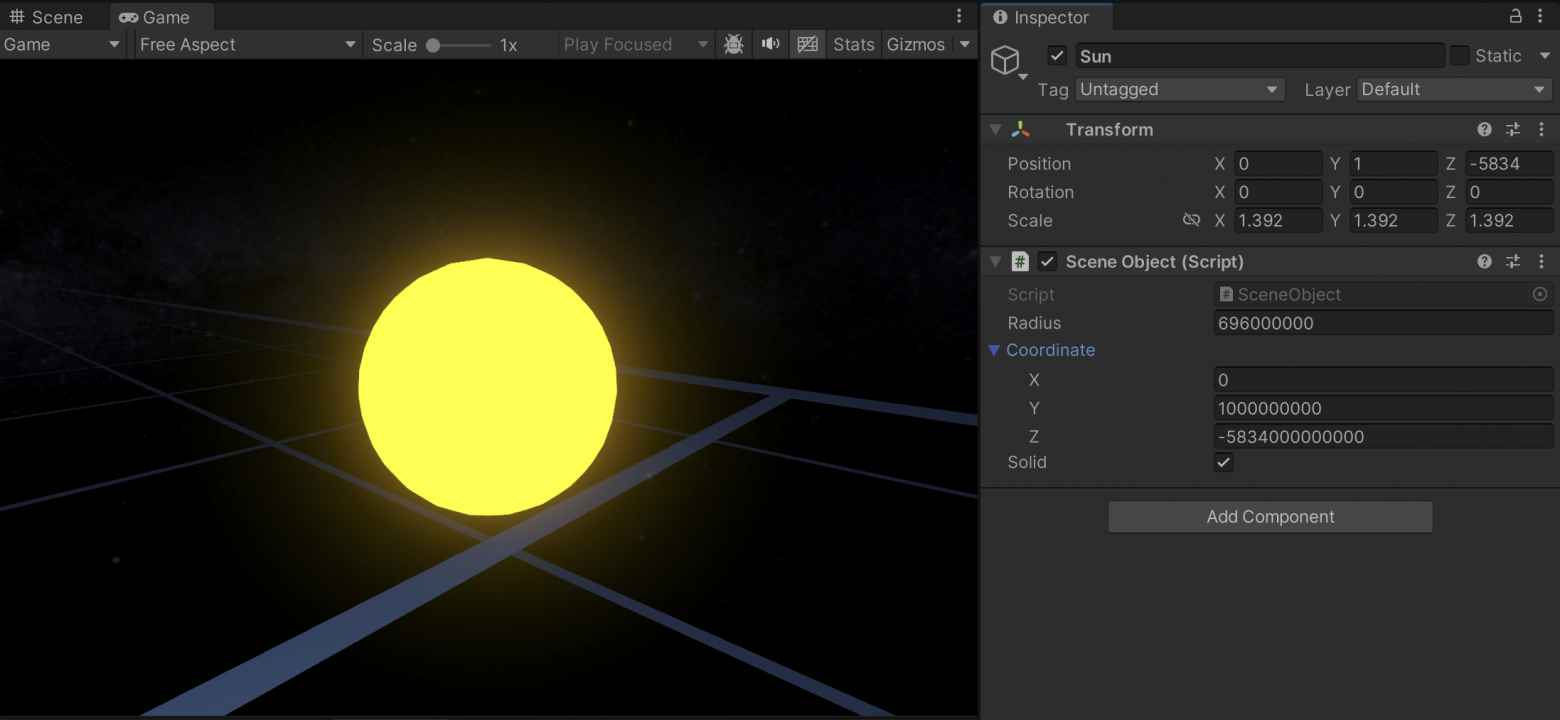
MeterToUnit = 1E-09Золотой стандарт. Метод плавающего центра координат
Техника плавающего центра координат (floating origin) широко применяется в играх, и не только в аспекте рендеринга, но и например для расчета физики объектов. Идея метода заключается в том, что постоянно или при выходе за границы какой-то области ко всем объектам в сцене (включая камеру) применяется одинаковый сдвиг, благодаря которому они оказываются ближе к центру координат.
В нашем случае проще реализовать непрерывный сдвиг координат, при котором камера всегда находится в центре координат и относительно нее смещаются все объекты сцены. Опишу алгоритм более формально:
Вне зависимости от координаты камеры, ей присваивается нулевая позиция
Из координат всех объектов вычитается координата камеры. Затем они так же как и в предыдущем методе умножаются на коэффициент
MeterToUnit, и полученные значения присваиваются позициям соответствующих объектов в сценеРазмеры объектов так же рассчитываются через умножение на
MeterToUnit
Еще раз напоминаю, что система рендеринга никогда не меняет координаты объектов и камеры - они для нее только входные данные. Но она может рассчитывать их итоговые позиции в сцене как ей заблагорассудится, это её бизнес-логика. При работе с координатами, система рендеринга работает с типом Vector3d, и конвертация в Vector3 происходит на самом последнем этапе, что позволяет сохранять точность при расчетах.
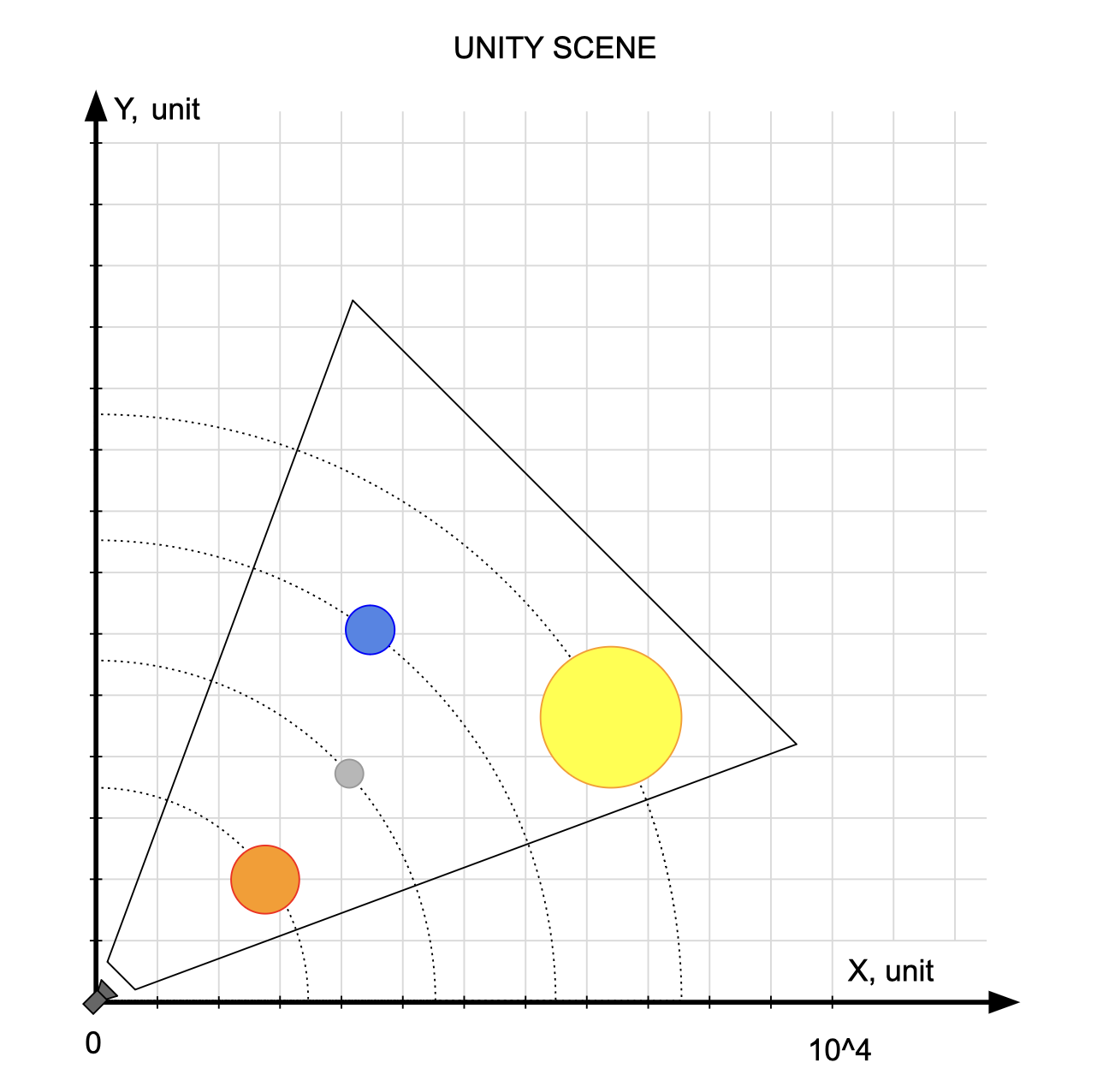
Таким образом, если камера расположена около того же многострадального Плутона, то его позиция в сцене относительно камеры (и соответственно центра координат сцены) будет маленькой, и не создаст проблем с точностью - он не будет трястись. Разумеется, при таком расположении камеры, уже позиция Меркурия в сцене станет далекой от центра, но его тряску (да и его самого) мы не увидим - слишком далеко. Казалось бы, проблема решена?
MeterToUnit = 1E-09, Scale все так же мал, но и Position близок к нулю - Плутону норм Не совсем. Проблема с ближней плоскостью клипирования, описанная в предыдущем методе, никуда не делась. Минимальную дальность плоскости клипирования 0.01f уменьшить нельзя, мы можем только увеличить MeterToUnit чтобы увеличить масштаб пространства и отодвинуть объект от камеры в сцене, но тогда во-первых возрастут расстояния между объектами, а во-вторых их собственные размеры так же станут слишком большими. Логика плавающего центра координат сохранит точность для объектов около камеры, но чтобы дальние объекты (которые при большом MeterToUnit окажутся еще дальше) все еще попадали в область видимости камеры, нам придется отодвигать дальнюю плоскость клипирования (FarClip) на очень большое расстояние, а за этим следует еще одна принципиальная проблема.
Одним из этапов рендеринга является z-буферизация, в ходе которой для каждого пикселя кадра определяется дальность от отображенного на нем объекта сцены до камеры. Разрядность z-буфера фиксирована, поэтому его разрешение зависит от расстояния от ближней плоскости клипирования до дальней, и чем оно больше, тем точность меньше. Распространенным багом, связанным с проблемой точности z-буфера является так называемый z-конфликт, когда два объекта имеющие близкие z-координаты начинают поочередно перекрывать друг друга в зависимости от точки обзора, иногда смешиваясь с образованием полосатого узора.
Ограничение точности z-буфера не позволяет нам бесконечно отодвигать дальнюю плоскость клипирования. Если мы все же попытаемся это сделать и выставим экстремальные значения FarClip, то увидим весьма разнообразные графические баги, например:
Нарушение порядка отрисовки объектов - даже далекое от Земли Солнце иногда рисуется поверх нее
Некоторые объекты при определенном удалении станут полно��тью черными
Скайбокс может деформироваться или полностью исчезать

Выводы
Результат все так же неудовлетворительный. Устранена тряска далеких объектов, но проблемы с маленькими объектами не решены
Метод был бы пригоден, если объекты имели сопоставимые размеры, тогда можно было бы подобрать параметры при которых они бы все отображались корректно
Метод очень прост в реализации
Геометрический хак. Метод конического масштабирования
Давайте временно забудем об инфографических объектах (плоскость эклиптики, высоты) и посмотрим, из чего состоит наша сцена? Она состоит из сфер разного радиуса, которые не пересекаются (мы не моделируем столкновения планет), и обычно расположены друг от друга на приличном расстоянии.

Если сцена состоит только из сфер, то обязательно ли нам по-честному расставлять их в сцене и присваивать им истинные размеры (путь даже и единообразно отмасштабированные)? Ответ - нет, не обязательно. Надо помнить, что пользователь не видит сцену Unity, пользователь видит только итоговый кадр, и нам нужно сделать так, чтобы в нем объекты выглядели так, как выглядели бы объекты таких размеров в реальности, а то как это было достигнуто - исключительно наше дело.
В пределе, такую задачу можно было бы решить без применения средств 3D графики, а просто рисуя спрайты на двухмерном холсте (Canvas). Действительно, ведь мы знаем точные координаты объектов, значит мы можем их отсортировать по дальности от камеры а затем просто рисовать по очереди от более дальнего к самому ближнему, выставляя масштаб в зависимости от расстояния и радиуса объекта.
Примерно на такой идее строится этот метод, но без ухода в крайность - мы все же будем работать с трехмерной сценой, ведь у нас нет готовых спрайтов объектов - у нас есть полигональные модели, которые к тому же в теории могут иметь произвольный поворот. В этом методе применяется прием, который я называю “коническое масштабирование”.
Он заключается в том, что объект в сцене можно невозбранно двигать вдоль его “конуса видимости”, при этом уменьшая его при приближении к камере и увеличивая при удалении, чтобы компенсировать изменение размера в кадре от влияния перспективной проекции. Разумеется, такое преобразование может нарушить порядок объектов в сцене, но мы можем попробовать это учесть.
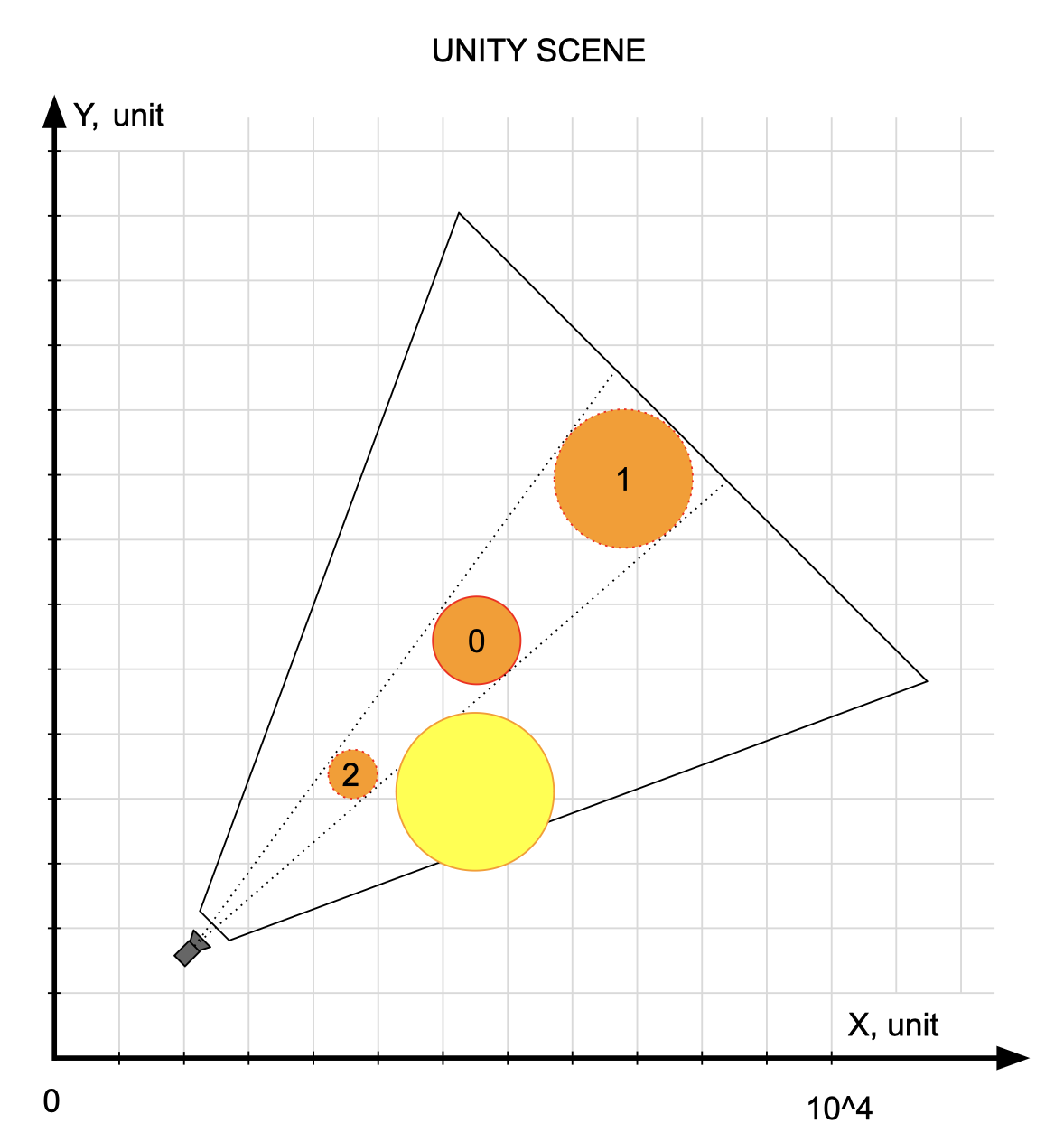
Предлагаемый алгоритм выглядит так:
Камера всегда выставляется в нулевую позицию
Формируется массив из объектов сцены, отсортированный по возрастанию расстояния от камеры
Если камера попала внутрь какого-то объекта то он скрывается и не обрабатывается дальше
Для каждого объекта формируется “радиальный слой”: мы сохраняем направление от объекта до камеры, нормализуем его (превращаем в единичный вектор) и умножаем на текущий радиус слоя. При переходе к следующему объекту, к радиусу слоя прибавляется фиксированный шаг
Масштаб объекта рассчитывается на основе его радиуса, с учетом изменения расстояния от камеры с исходного до фактического
Применяя этот метод мы перестраиваем сцену, выстраивая на небольшом расстоянии перед камерой все объекты, но так как перестройка происходит перед каждым рендерингом кадра то пользователь этого не замечает. В рамках данного способа мы решаем и проблему с большими координатами объектов и с их размерами, а так же устраняем проблему с точность z-буфера камеры.
Пока что все выглядит неплохо, можно ли считать этот способ готовым решением? К сожалению нет, есть две проблемы.
Во-первых в такой метод нельзя полноценно интегрировать инфографические объекты, ведь мы фактически ломаем геометрию сцены, и это остается незамеченным лишь потому что эти объекты никак не соединены между собой. Если бы нам требовалось рисовать линии между объектами, то они бы никак не вписались в эту систему. В нашем проекте линий между объектами нет, но есть сетка плоскости эклиптики и линии высот объектов над ней. Конечно можно придумать разные трюки, например привязать их к первому объекту и масштабировать вместе с ним, но в любом случае о их правильной сортировке с остальными объектами можно забыть. Тем не менее, для того что бы различать инфографики и реальные объекты как раз используется флаг Solid.

Во-вторых надо признать, что наш алгоритм сортировки объектов по дальности не всегда работает корректно. Например, если поставить маленький объект близко к большому, то при некоторых положениях камеры расстояние до него будет ближе чем расстояние до центра большого объекта, что ломает нашу логику. Если подумать, то наверное можно придумать что-то получше (например применить рейкаст), но из-за того что у этого метода и так уже есть неустранимая проблема, описанной в первом пункте, я не стал копать глубже.

Выводы
Метод концептуально прост, но требует доработки и тонкой настройки
Оценка результата зависит от задачи, но все же в наших условиях он не годится
Метод обычно работает для удаленных друг от друга объектов и при отсутствии инфографик, поэтому можно подумать о его применении в задачах где эти условия соблюдаются
Алгоритм сортировки объектов требует доработки
Ультимативное решение. Многослойный рендеринг
Итак, в предыдущих методах мы смогли побороть отдельные проблемы рендеринга космических объектов, но так и не получили универсального решения, которое удовлетворяло бы всем нашим требованиям. Я предлагаю вернуться ко второму методу - плавающему центру координат, и вспомнить чего нам не хватило для победы. В нем мы справились с проблемой дрожания удаленных объектов, но столкнулись с недостатком точности z-буфера. Мы не можем увеличить точность z-буфера напрямую, но мы можем попробовать разбить пространство по дальности на слои и рендерить их отдельными камерами, у каждой из которых буфер будет свой. Этой идеей можно коротко описать всю суть описанного далее метода.
Рассмотрим предлагаемый алгоритм более подробно:
Находим в сцене объекты "ближней зоны" - те объекты, которым грозит обрезка из-за ближней плоскости клипирования камеры. Если таких объектов нет, то переходим сразу к пункту 5
Сортируем объекты по дальности от камеры
Формируем слои для этих объектов. Рассчитываем специфичный для каждого слоя
MeterToUnitтак, чтобы самый близкий к камере объект слоя не обрезался ближней плоскость клипирования, а так же рассчитываем “толщину” слоя так, чтобы она не превышала заданный лимит (и точности z-буфера хватило). При этом формируем столько слоев, сколько нужно чтобы охватить все ближнее пространство по дальности, поэтому все последующие слои начинаются сразу после предыдущего без единого разрыва. Рассчитываем с учетомMeterToUnitкоординаты и размеры объектов в рамках слоя, так же применяя логику плавающего центра координат.
Эта процедура выполняется для всех объектов, но в зависимости от флагаSolidсистема по-разному реагирует на попадание камеры внутрь объекта, соответственно для инфографик она делает вид что ничего не произошло и рендерит их с фиксированной близкой дальности изнутри, а реальные объекты скрывает, потому что они не рассчитаны на это. НоSolidэто не синонимReal, к примеру кольца Сатурна реальный объект, но камера может влететь внутрь негоПод каждый слой создаем (точнее - активируем из пула) новую камеру, и вешаем на нее коллбек, чтобы перед началом ее рендеринга выставить объектам слоя нужные позиции и масштабы
Для всех остальных объектов (так называемой "дальней зоны") применяем обычную логику метода плавающего центра координат с единой камерой и фиксированным
MeterToUnitРендеринг камер происходит по очереди, от камеры дальнего слоя к ближнему. Результаты рендеринга камер накладываются друг на друга, формируя итоговый кадр
MeterToUnit, поэтому показать итоговое расположение объектов в них на одном рисунке нельзя

Разумеется такое описание алгоритма не отражает всех деталей реализации и настроек - их можно посмотреть в исходном коде проекта. Скажу лишь что поиск объектов ближней зоны отнюдь не является тривиальной задачей.
Про задачу поиска объектов ближней зоны
Задачу о поиске объектов ближней зоны можно сформулировать так: в трехмерном пространстве имеется пирамида (причем не усеченная, как обычно бывает для камеры) и сфера, их параметры известны. Они могут иметь произвольное расположение и поворот (это важно для пирамиды но не важно для сферы). Требуется определить: 1) пересекаются ли эти объекты 2) если да, то нужно найти глубину самой ближней и самой дальней точки сферы, попавшей внутрь пирамиды.
Возможно кому-то эта задача покажется простой, особенно если рассматривать ее как двухмерную, но уверяю вас, в ней есть груда подводных камней. Сфера может обрезаться пирамидой по-разному, иногда точки пересечения являются границами по дальности, иногда - нет. Камера может находиться внутри сферы, тогда все равно надо найти глубину ее последней точки. Наконец, трехмерный случай нельзя собрать просто из решения этой задачи для двух плоскостей.
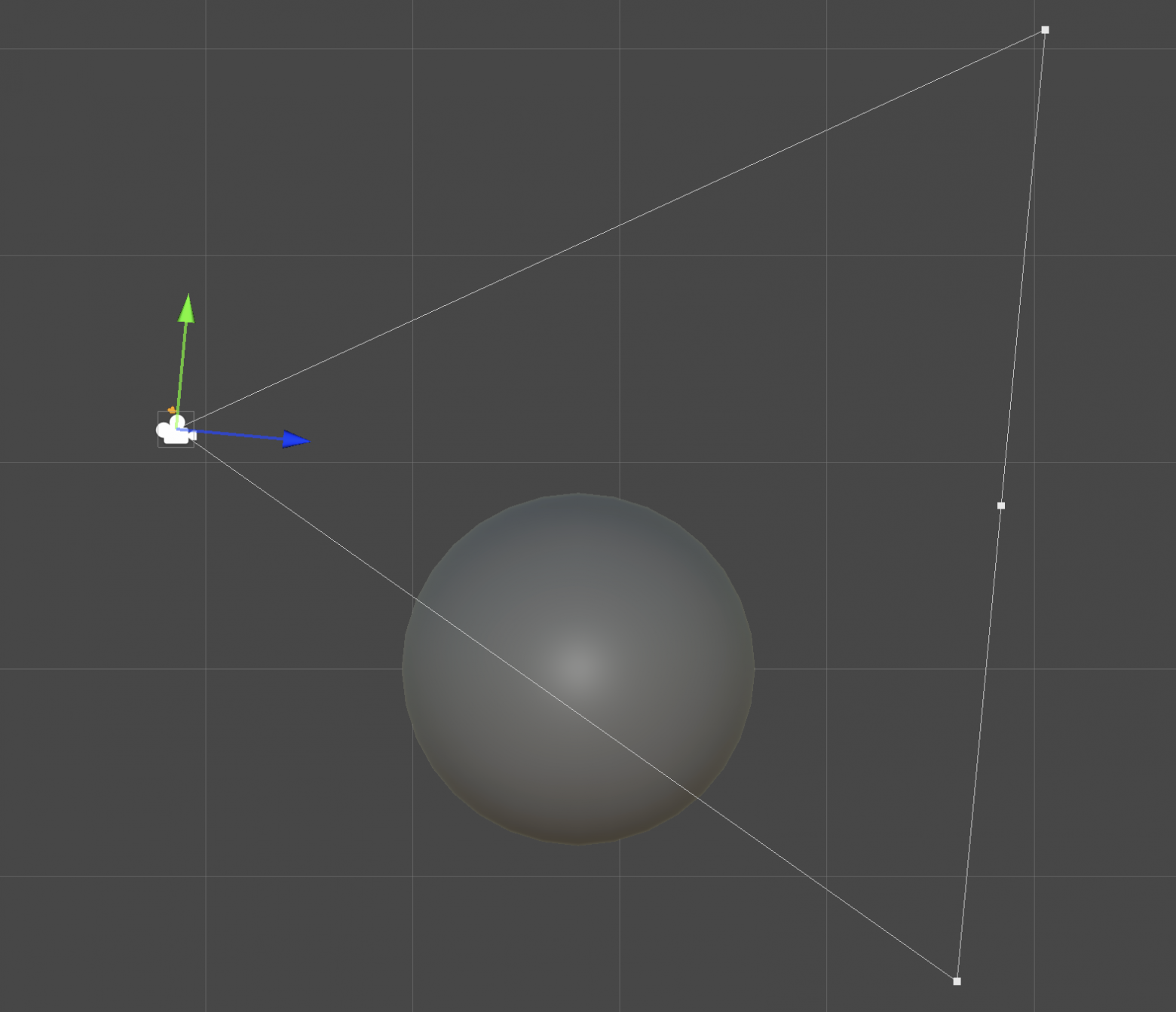
Но в итоге я решил эту задачу, общая идея решения в том, что для каждой боковой грани пирамиды отдельно проверяется пересечение со сферой, и в свою очередь, в рамках каждой грани алгебраически ищутся точки пересечения окружности с прямыми, формирующими эту грань. Важным ходом в процессе решения так же является применение к локальным координатам сферы обратного кватерниона поворота самой пирамиды. Это позволяет полностью устранить из игры произвольный поворот пирамиды. Фактически мы считаем ее намертво приклеенной к осям, и вместо этого просто поворачиваем весь мир вокруг нее, что для сфер имеет результат только в сдвиге координат.
Так как итоговое изображение строится на основе склеивания отдельных слоев, важно чтобы границы этой склейки не были видны. Это достигается выставления правильных настроек системы, в частности нельзя допускать чтобы внутри слоев были проблемы с точностью z-буфера. Для увеличения точности слоя его нужно делать мельче, а чем мельче слои тем больше требуется камер, поэтому тут важно найти баланс между точностью и производительностью.

Тем не менее, в тестовом проекте этого удалось добиться, и дефекты склейки слоев встречаются только тогда, когда камерой режется плоскость эклиптики. Эту проблему при желании можно решить, если заменить одну плоскость с адским масштабом несколькими отдельными моделями.

Выводы
Метод решает поставленные задачи. Иногда на стыке слоев больших объектов возникают артефакты, но с ними можно бороться
Метод использует несколько камер а так же множество вычислений, что делает его менее производительным чем предыдущие
Метод заметно сложнее предыдущих в реализации
Общий вывод
Как мы видим, для поставленной в этой статье задачи подошел только последний метод, но это не значит что остальные не имеют права на существование. Я считаю что самый лучший метод этот тот, который решает задачу самым простым способом, поэтому важно понимать границы применимости разных подходов и уметь выбрать лучший в зависимости от условий, при необходимости модифицируя его с учетом специфики проекта или даже комбинируя с другими.
Исходный код проекта
Unity-проект со всем исходным кодом проекта доступен по ссылке. Хотя для этого проекта использовались только бесплатные ассеты, в соответствии с лицензией стора я не имею права публиковать их в открытом доступе. В ближайшее время я подготовлю небольшую инструкцию как интегрировать графику в проект самостоятельно.
Прошу учесть, что этот проект не представляет собой готовое решение из коробки а является тестовым стендом для отработки технологий. В связи с этим, при написании кода я старался ставить простоту и читаемость в абсолютный приоритет над любыми (даже очевидными) оптимизациями, в частности:
Некоторые переменные объявлены только для удобства чтения и отладки
Vector.magnitude используется даже там, где можно применять sqrMagnitude
List применяется там, где можно обойтись массивом с максимальной фиксированной длиной, в случае если число элементов не очевидно заранее
Для более глубокого управления рендерингом можно было бы использовать Unity Scriptable Render Pipeline, но я обошелся и без него
И многое другое
Тем не менее, проект не имеет проблем с производительностью в редакторе, по крайней мере на моей машине (MacBook Pro M1)
WebGL билд проекта можно посмотреть здесь
Мемчик

