ВВЕДЕНИЕ
Медицинские исследования играют важную роль в понимании различных заболеваний и разработке эффективных методов лечения. Одним из инструментов, используемых в кардиологии, является фонокардиограмма (ФКГ).
Фонокардиограмма - это метод диагностики сердечно-сосудистой системы, который основывается на записи звуков, производимых сердцем. Она может быть полезной в определении различных заболеваний сердца, таких как стеноз клапана, митральный стеноз, митральную недостаточность, перикардит и другие.
ФКГ може�� использоваться для оценки эффективности лечения сердечных заболеваний и для наблюдения за состоянием сердца в течение времени. Если у вас есть симптомы, такие как боль в груди, одышка, учащенный пульс, упадок сил, обратитесь к кардиологу, который посоветует, нужна ли вам ФКГ [1].
Объектом исследования выпускной квалификационной работы является список файлов формата .csv, содержащих разделенные знаком ";" смещенные целочисленные значения амплитуды шумов сердца, записанные в течение нескольких секунд, частота дискретизации – 1000 гц (числа в записи обозначают амплитуду сигнала, временной промежуток между соседними значениями - 1 миллисекунда).
Цель работы состоит в создании алгоритма автоматической интерпретации снятых данных, который пытается по форме кривых делать выводы, аналогичные тем, которые по этим же кривым умеет делать эксперт и создание собственного алгоритма. Необходимо определить и выделить точку максимальной амплитуды, начало и окончание тона 1 для каждого из сердечных циклов. Ответ необходимо вывести в виде списка списков [t1, t2, t3], где t1 – начало тона 1, t2 – точка максимальной амплитуды, t3 – окончание тона 1. Также, для проверки результата, необходимо визуализировать полученный результат на графике. Данную процедуру необходимо произвести для каждого файла.
Для достижения поставленной цели в процессе работы будут выполнены:
· Получение предметной области (фонокардиограммы и ее интерпретации) и ее описание,
· Изучение алгоритмов анализа данных
· Изучение навыков работы с файлами в формате .csv
· Разработка плана алгоритма по анализу данных
· Программная реализация созданного алгоритма на языке python
· Анализ полученных данных
Актуальность данной темы ВКР заключается в возможности применения улучшенного алгоритма на практике при обследовании пациентов и в больших исследовательских проектах, связанных исследованием сердца. Это особенно важно в наше время, так как заболевания сердечно-сосудистой системы являются лидером по количеству смертей в мире (18,56 млн. в 2019 году, по оценкам американского Института измерения показателей и оценки состояния здоровья).
Ссылка на github с кодом: medical_date/script.py at main · ReshetnikovDmitrii4918/medical_date (github.com)
1. Изучение предметной области и ее описание
1.1. Определение ФКГ
Медицинские исследования играют важную роль в понимании различных заболеваний и разработке эффективных методов лечения. Одним из инструментов, используемых в кардиологии, является фонокардиограмма (ФКГ). Она может использоваться для диагностики многих заболеваний сердца, таких как:
· Ишемическая болезнь сердца
· Аритмия сердца
· Застойная сердечная недостаточность
· Врожденные пороки сердца
· Перикардит (воспаление оболочки сердца)
· Миокардит (воспаление мышцы сердца)
· Клапанные пороки сердца
Сердце - это один из самых важных органов человеческого организма, поскольку оно отвечает за кровообращение, необходимое для жизни.
Сердце работает как насос, который откачивает кровь через кровеносные сосуды, доставляя кислород и питательные вещества во все органы и ткани тела. Кроме того, сердце удаляет отработанные продукты обмена веществ и углекислый газ, который выделяется при дыхании.
Несоответствие работы сердца может привести к серьезным заболеваниям, которые могут существенно ухудшить качество жизни, снизить работоспособность, а в некоторых случаях могут быть смертельными.
Сердце производит два основных звука, называемых первым и вторым тонами. Первый тон связан с закрытием митрального и трикуспидального клапанов во время систолы, а второй тон связан с закрытием аортального и легочного клапанов во время диастолы. Первый тон более низкий и короткий, чем второй тон [6].
Фонокардиограмма – это метод записи звуков, которые производит сердце во время систолы и диастолы. ФКГ отображает звуковые волны, которые передаются по коже груди человека во время систолы и диастолы. Эти звуковые волны затем усиливаются и записываются на бумагу или электронный носитель [2].
ФКГ (Функционально-Категориальная Грамматика) - это одна из лингвистических теорий, которая описывает язык как систему грамматических категорий и функций. Она развивалась с 70-х годов XX века в работах лингвистов из Европы и США, включая Саймона Дикса, Пола Хёнеманна и других.
Основной принцип ФКГ заключается в том, что смысл выражается через функции, которые слова и ��ыражения выполняют в предложении. Функции определяются на основе категорий, которые могут быть выражены различными частями речи, такими как существительные, глаголы, прилагательные и т.д [3].
В ФКГ грамматика рассматривается как средство обеспечения коммуникации, а не просто правила, которые нужно следовать. Таким образом, ФКГ ориентирована на анализ реальных языковых данных и на поиск того, как грамматика функционирует в речевой практике [4].
Пример того, как выглядит ФКГ в соответствии с рисунком 1.

1.2. История ФКГ
Фонокардиограмма (ФКГ) – это метод исследования сердечной деятельности, который использует запись звуков, генерируемых сердцем в процессе его работы [5]. История ФКГ начинается в 1902 году, когда русский врач и ученый Николай Сергеевич Коротков представил свой изобретенный стетоскоп с двухсторонней мембраной. С помощью этого стетоскопа он смог записать сердечные звуки и зарегистрировать их изменения в процессе сердечной деятельности.
Однако, развитие ФКГ как метода диагностики сердечных заболеваний началось в 1950-х годах, когда появились первые специализированные устройства для записи и анализа звуков сердца. В 1953 году американский кардиолог Paul Wood описал в своей книге "Diseases of the Heart and Circulation" метод записи и анализа звуков сердца, который позже стал известен как ФКГ.
С тех пор ФКГ стали широко использоваться в медицине для диагностики различных заболеваний сердца, таких как пороки сердца, ишемическая болезнь сердца, аритмии и другие. Современные устройства для записи и анализа звуков сердца позволяют получать более точные и детальные данные о функционировании сердца и сокращать время, необходимое для проведения исследований.
С развитием информационных технологий и компьютерных методов анализа данных, возникла возможность автоматизировать процесс анализа ФКГ, что повышает точность диагностики сердечных заболеваний и сокращает время их обнаружения. Разработка программного обеспечения для автоматической обработки ФКГ является актуальной задачей в области медицинских исследований.
1.3. Принцип работы ФКГ
Принцип работы ФКГ основан на регистрации звуковых волн, которые производятся при работе сердца, и передаются через кожу груди пациента. ФКГ-аппарат состоит из микрофона, усилителя, фильтра и записывающего устройства.
Во время исследования пациент лежит на кушетке и на его груди размещают микрофон, который регистрирует звуки, производимые сердцем. Эти звуки усиливаются усилителем и проходят через фильтр, который удаляет шумы и артефакты, не связанные с сердечной работой [7].
После фильтрации звуки записываются на бумаге или в электронной форме. Электронная форма записи ФКГ позволяет более детально анализировать данные, проводить автоматическую обработку и сохранять результаты в электронном виде.
1.4. Преимущества фонокардиограммы
Существует несколько преимуществ фонокардиограммы по сравнению с другими методами исследования сердца:
· Неинвазивность. Фонокардиограмма - неинвазивный метод диагностики, что означает, что нет необходимости в проникновении внутрь тела пациента, что может уменьшить риск возникновения осложнений и нежелательных побочных эффектов.
· Нет необходимости специальной подготовки. Фонокардиограмма не требует специальной подготовки пациента, в отличие от других методов диагностики сердечно-сосудистой системы, таких как коронарография.
· Доступность. Фонокардиограмма относительно дешевый и широко доступный метод диагностики, который может использоваться в большинстве медицинских учреждений.
· Полезность в диагностике определенных заболеваний. Фонокардиограмма может быть особенно полезной в диагностике некоторых заболеваний сердца, таких как митральный стеноз, при котором клапан между левым предсердием и левым желудочком не открывается полностью, что приводит к сужению прохода и повышению давления в легочной артерии.
Однако, не следует забывать, что фонокардиограмма имеет свои ограничения, и ее результаты должны интерпретироваться в сочетании с другими методами диагностики. Кроме того, результаты фонокардиограммы могут быть неправильно интерпретированы, если пациент имеет заболевания легких или грудной клетки.
1.5. Процедура дискретизации сигнала
Процедура дискретизации сигнала - это процесс преобразования аналогового сигнала в цифровой формат. Дискретизация используется для хранения и обработки сигналов в компьютерных системах и других устройствах.
Процедура дискретизации состоит из следующих шагов:
· Определение частоты дискретизации (sampling rate) - это количество отсчетов сигнала, производимых за секунду. Частота дискретизации измеряется в герцах (Гц) и обычно должна быть достаточно высокой, чтобы сохранить достоверность исходного сигнала. Чем выше частота дискретизации, тем больше точность результата, но и больше объем полученных данных [8].
· Измерение аналогового сигнала на протяжении определенного периода времени. Для этого используется аналогово-цифровой преобразователь (ADC) [5].
· Конвертация аналогового сигнала в цифровой формат. Аналоговый сигнал амплитуды в каждый момент времени переводится в соответствующее цифровое значение.
· Хранение полученных данных в цифровом формате для дальнейшей обработки.
После процедуры дискретизации, цифровой сигнал может быть обработан и передан для дальнейшего использования в различных цифровых устройствах. Однако, важно помнить, что процесс дискретизации не является обратимым, и потери точности могут возникнуть в процессе перевода аналогового сигнала в цифровой формат. Поэтому, при выборе частоты дискретизации необходимо учитывать специфики и требования конкретной задачи, а также возможные ограничения оборудования [9].
Примеры процедуры дискретизации сигнала представлены в соответствии с рисунком 2.

1.6. Типовые значения дискретизации фонокардиограммы
Типовые значения частоты дискретизации фонокардиограммы составляют от 1000 до 4000 Гц. Однако, в некоторых случаях может использоваться и более высокая частота дискретизации для получения более точных результатов. Важно учитывать, что частота дискретизации должна быть достаточно высокой, чтобы сохранить все важные компоненты сигнала, но при этом не должна быть слишком высокой, чтобы не возникло проблем с объемом данных и вычислительной сложностью анализа.
Кроме того, при выборе частоты дискретизации необходимо учитывать особенности оборудования, используемого для записи фонокардиограммы. Например, если используется аналоговый микрофон, то частота дискретизации должна быть достаточно высокой, чтобы избежать потери качества сигнала при его преобразовании в цифровой формат.
Для анализа фонокардиограммы используются различные методы обработки сигналов, такие как фурье-анализ, вейвлет-анализ и другие. Однако, для успешного применения этих методов необходимо иметь качественный и достаточно точный сигнал, полученный при правильной частоте дискретизации.
В целом, выбор частоты дискретизации фонокардиограммы зависит от конкретной задачи и доступных ресурсов. Однако, при выборе частоты необходимо учитывать особенности оборудования и возможности анализа данных, чтобы получить наиболее точные и полезные результаты.
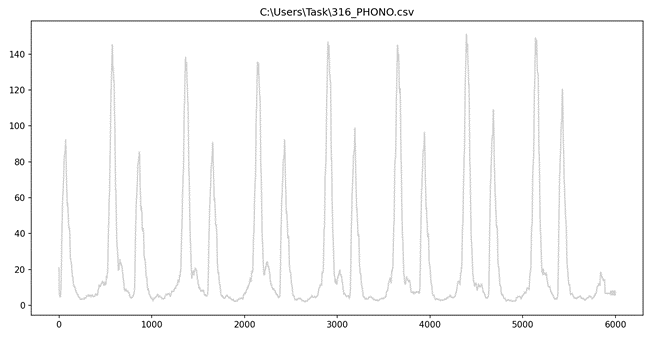
Пример фонокардиограммы с большим количеством шумов представлен в соответствии с рисунком 3.
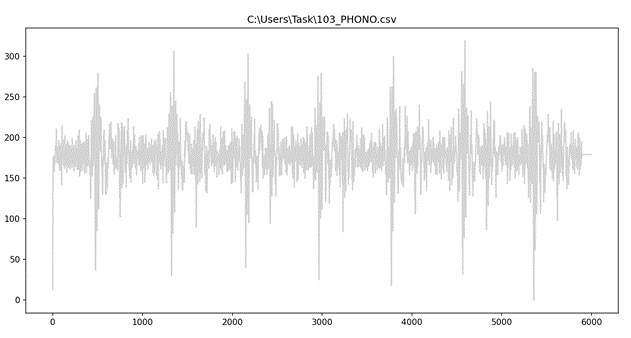
1.7. Свойства фонокардиограммы
Фонокардиограмма (ФКГ) - это графическое изображение звуковых сигналов, которые возникают в процессе работы сердца, и которые можно записать с помощью фонокардиографа. ФКГ имеет несколько свойств, которые могут быть полезны при диагностике заболеваний сердца. Некоторые из них описаны ниже:
· Амплитуда звука. ФКГ отображает амплитуду звуковых сигналов, возникающих в сердце. Нормальные звуки сердца обычно имеют характерные амплитуды, которые могут изменяться при наличии патологии.
· Частота звука. ФКГ также может показывать частоту звука, который производит сердце. Например, первый звук (S1) часто имеет более низкую частоту, чем второй звук (S2).
· Длительность звука. ФКГ может отображать длительность звуковых сигналов, которые производит сердце. Нормальные звуки сердца обычно имеют характерную длительность, которая может изменяться при наличии патологии.
· Характеристики звука. ФКГ может также показывать различные характеристики звуковых сигналов, такие как наличие шумов, ритмичность звуков, асимметричность звуков, и т.д.
· Временные интервалы между звуками. ФКГ может отображать временные интервалы между звуками, которые производит сердце.
В качестве наглядного примера представлены 2 рисунка. В соответствии с рисунком 4, изображена фонокардиограмма здорового человека, в соответствии с рисунком 5 изображена фонокардиограмма человека при митральном стенозе. Фонокардиограмма при митральном стенозе: видны увеличение амплитуда и частоты I тона сердца («хлопающий тон I»), тон открытия митрального клапана (М) и предшествующий I тону пресистолический шум (указан стрелками).
Митральный стеноз - это заболевание сердца, при котором стенка между левым предсердием и левым желудочком становится узкой, что затрудняет нормальный кровоток и может привести к сердечной недостаточности. Симптомами митрального стеноза могут быть одышка, усталость, отеки, боли в груди и снижение физической выносливости. Лечение может включать медикаментозную терапию, а также хирургическое вмешательство в виде расширения или замены стенки между предсердием и желудочком.


Ориентировочные значения частот и амплитуд фонокардиограммы зависят от конкретной ситуации и могут варьироваться. Однако, обычно на фонокардиограмме можно увидеть основные звуки сердца - первый тон (S1), который происходит при закрытии митрального и трикуспидального клапанов, и второй тон (S2), который происходит при закрытии аортального и легочного клапанов. Частоты этих звуков обычно находятся в диапазоне 20-200 Гц, а амплитуды могут варьироваться в зависимости от состояния сердца и других факторов. Дополнительные звуки, такие как третий тон (S3) или четвертый тон (S4), могут также быть видны на фонокардиограмме и иметь свои собственные частоты и амплитуды.
Длительность фонокардиограммы зависит от длительности сердечного цикла и может составлять от 0,5 до 1,5 секунд. Интервалы между звуками на фонокардиограмме также имеют свои нормы и могут варьироваться в зависимости от состояния сердца. Например, интервал между S1 и S2 (систолический интервал) обычно составляет около 0,3-0,4 секунды, а интервал между S2 и следующим S1 (диастолический интервал) - около 0,4-0,5 секунды. Однако, эти значения могут изменяться при различных патологиях сердца.
Фонокардиограмма показывает нормальный ритм сердца, отсутствие шумов и аномалий звуков сердечных клапанов. Она может быть ограничена тем, что не всегда способна выявить другие сердечно-сосудистые заболевания, такие как ишемическая болезнь сердца или аритмии, и может потребоваться дополнительная диагностика.
На фонокардиограмме можно выделить несколько основных звуковых сигналов:
· Первые тоны (S1) – возникают в результате закрытия митрального и трикуспидального клапанов в начале систолы. Этот звук имеет низкую частоту и высокую амплитуду.
· Вторые тоны (S2) – возникают в результате закрытия аортального и легочного клапанов в конце систолы. Этот звук имеет более высокую частоту и меньшую амплитуду, чем S1.
· Третьи тоны (S3) – возникают при быстром наполнении желудочков кровью в начале диастолы. Этот звук имеет очень низкую частоту и низкую амплитуду.
· Четвертые тоны (S4) – возникают при сокращении предсердий и наполнении желудочков кровью. Этот звук имеет еще более низкую частоту, чем S3.
Пример фонокардиограммы с обозначением всех видов шумов представлен в соответствии с рисунком 6. I – первый тон, II – второй тон, III – третий тон, IV – четвертый тон.

Интерпретация звуковых сигналов на фонокардиограмме позволяет оценить работу сердца и выявить нарушения его функций. Например, увеличение амплитуды S3 может свидетельствовать о наличии нарушений в работе желудочков сердца, а появление S4 – о наличии нарушений в работе предсердий. Кроме того, изменение времени между S1 и S2 может свидетельствовать о наличии аритмии, а изменение формы звуковых сигналов может указывать на наличие пороков сердца [10].
1.8. Сравнительный анализ фонокардиограммы и электрокардиограммы в диагностике
Фонокардиограмма и электрокардиограмма (ЭКГ) - это два разных метода диагностики сердечно-сосудистых заболеваний. Фонокардиограмма основана на регистрации звуковых сигналов, которые создаются сердцем во время его работы, а ЭКГ - на регистрации электрических сигналов, которые возникают в сердце во время сокращения мышц [11].
Однако, несмотря на то, что фонокардиограмма и ЭКГ измеряют разные параметры сердца, они могут использоваться вместе для более точной диагностики сердечно-сосудистых заболеваний.
Например, при ишемической болезни сердца (ИБС) оба метода могут использоваться для определения наличия и местоположения ишемии (недостаточного кровоснабжения сердца). Фонокардиограмма может показать наличие шума в сердце, который может быть связан с недостаточным кровоснабжением, а ЭКГ - изменение электрической активности сердца.
Также, фонокардиограмма может быть полезна для диагностики других заболеваний сердца, таких как митральный стеноз, аортальный стеноз и гипертрофическая кардиомиопатия. В то же время, ЭКГ может использоваться для диагностики аритмий и других нарушений сердечного ритма.
В целом, фонокардиограмма и ЭКГ - это важные методы диагностики сердечно-сосудистых заболеваний, которые могут использоваться вместе для более точной оценки состояния сердца. Однако, для полной диагностики может потребоваться использование других методов, таких как ЭхоКГ, коронарография и др.
2. Алгоритмы для анализа фонокардиограммы
В теории, выбор алгоритма для анализа фонокардиограммы зависит от конкретной задачи, которую нужно решить. В общем случае, для анализа ФКГ используются следующие алгоритмы: фильтрация, сегментация, анализ частоты.
2.1. Сегментация
Сегментация сигнала - это процесс разделения сигнала на отдельные сегменты или фрагменты, которые имеют определенные характеристики или свойства. Этот процесс может быть использован в обработке сигналов, например, для анализа звуковых сигналов, изображений или видео.
Для выделения отдельных фаз сердечного цикла на сигнале ФКГ используется алгоритм сегментации. Сегментация позволяет выделить фазы сердечного цикла, такие как систола и диастола, и провести анализ каждой из них.
Алгоритмы сегментации сигнала могут быть основаны на различных методах, таких как пороговая обработка, анализ спектра, машинное обучение и т.д., Например, пороговая обработка может быть использована для выделения отдельных звуковых сигналов в записи, а анализ спектра может помочь в выделении определенных частотных компонентов.
В анализе пороговая обработка может использоваться для определения минимального объема данных, необходимых для достижения нужного уровня точности и достоверности результатов. Например, при проведении исследования определенной группы людей, пороговая разработка может помочь определить минимальное количество участник��в, необходимых для получения статистически значимых результатов. Также пороговая разработка может использоваться для определения минимального объема данных, необходимых для обучения модели машинного обучения или для проведения анализа временных рядов. В общем, пороговая разработка в анализе данных помогает определить минимальные требования для достижения нужного уровня точности и достоверности результатов.
Алгоритмы сегментации сигнала могут быть настроены на различные параметры, такие как размер сегмента, пороговые значения и т.д., чтобы достичь наилучшей производительности в конкретных условиях. Они могут быть использованы для различных приложений, таких как распознавание речи, анализ звуковых сигналов в музыке или в медицинских приложениях.
2.2. Фильтрация
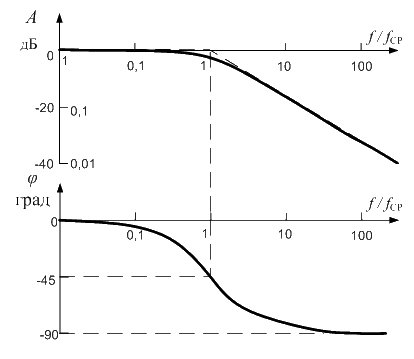
Для удаления шумов и артефактов из сигнала ФКГ применяются фильтры. Любой фильтр описывается частотной характеристикой. Эта характеристика показывает, как фильтр изменяет амплитуду и фазу сигнала при прохождении через него в зависимости от частоты. График амплитудно-частотной характеристики фильтра нижних частот представлен в соответствии с рисунком 7, а график фазо-частотной характеристики фильтра нижних частот представлен в соответствии с рисунком 8. Например, низкочастотный фильтр будет подавлять высокие частоты и сохранять низкие, а высокочастотный фильтр будет делать наоборот. Выбор определенного типа фильтра зависит от конкретной задачи и требуемых характеристик фильтрации. Для удаления шума из аудиосигнала может использоваться низкочастотный фильтр. Фильтр нижних частот - это алгоритм обработки сигнала, который позволяет удалять высокочастотные компоненты из сигнала и оставлять только низкочастотные [12]. Этот фильтр широко используется в обработке звука и изображений для устранения шума и улучшения качества сигнала. Фильтр нижних частот работает путем пропускания сигнала через фильтр с определенной частотной характеристикой, которая позволяет пропускать только низкочастотные компоненты. В качестве примера работы фильтрации в соответствии с рисунком 9. На рисунках желтым цветом изображены графики после фильтрации, а синим до фильтрации.
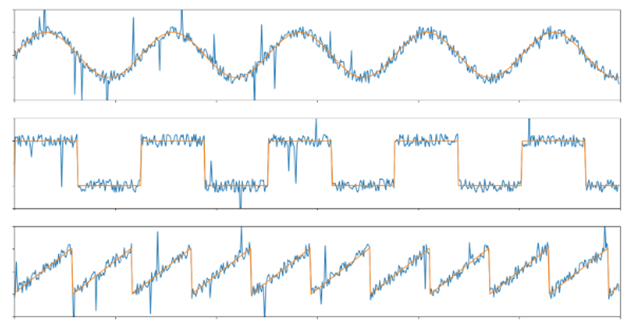
Один из методов шумоподавления - это медианный фильтр. Он используется для удаления шума из сигнала, основываясь на медианном значении. Медианное значение - это значение, которое находится в середине отсортированного списка значений. Медианный фильтр работает следующим образом: он берет определенное количество значений (например, 3, 5 или 7) и сортирует их по порядку. Затем он выбирает медианное значение и заменяет текущее значение в сигнале на это медианное значение. Этот процесс повторяется для каждого значения в сигнале. Медианный фильтр хорошо работает с шумами, которые имеют небольшую амплитуду и не являются коррелированными с полезным сигналом. Однако, если шум имеет большую амплитуду или коррелирован с полезным сигналом, то медианный фильтр может привести к потере полезной информации. Формула медианного фильтра:
Рекурсивный фильтр - это метод шумоподавления, который использует предыдущие значения сигнала для вычисления текущего значения. Он работает путем применения линейного фильтра к последовательности значений сигнала. Рекурсивный фильтр использует коэффициенты фильтра, которые определяют, как предыдущие значения сигнала будут влиять на текущее значение. Коэффициенты фильтра могут быть настроены для достижения определенных целей шумоподавления, таких как уменьшение шума или сохранение полезной информации. Рекурсивный фильтр может быть эффективным методом шумоподавления для сигналов с высоким уровнем шума, но он может быть чувствителен к выбросам и неустойчив к изменениям входных данных. Формула рекурсивного фильтра:
Нерекурсивный фильтр - это метод шумоподавления, который не использует предыдущие значения сигнала для вычисления текущего значения. Он работает путем применения линейного фильтра к последовательности значений сигнала без использования обратной связи. Нерекурсивный фильтр использует только текущее значение сигнала и некоторое количество предыдущих значений для расчета текущего значения. Коэффициенты фильтра могут быть настроены для достижения определенных целей шумоподавления, таких как уменьшение шума или сохранение полезной информации. Нерекурсивный фильтр может быть менее чувствительным к выбросам и более устойчивым к изменениям входных данных, чем рекурсивный фильтр. Однако он может быть менее эффективным для сигналов с высоким уровнем шума, чем рекурсивный фильтр. Формула нерекурсивного фильтра:
2.3. Анализ частоты
Для анализа частотных характеристик ФКГ используются спектральные анализаторы. Спектральный анализ позволяет выделить частоты, которые соответствуют отдельным компонентам звукового сигнала ФКГ.
В контексте анализа данных, спектральный анализ - это метод, который позволяет проанализировать временные ряды данных, разложив их на частотные компоненты и определив, какие частоты присутствуют в данных. Этот метод может быть полезен для выявления периодических закономерностей в данных, таких как сезонность или цикличность.
Процесс спектрального анализа включает в себя несколько шагов. Сначала данные анализируются с помощью преобразования Фурье, которое разбивает временной ряд на частотные компоненты. Затем производится анализ полученных компонент, чтобы определить, какие частоты присутствуют в данных.
Спектральная характеристика Фурье - это представление сигнала в частотной области. Она показывает, какие частоты присутствуют в сигнале и какая амплитуда у каждой частоты. Спектральная характеристика Фурье может быть получена с помощью преобразования Фурье, которое переводит сигнал из временной области в частотную область.
Преобразование Фурье - это математический метод, который позволяет перевести сигнал из временной области в частотную область. Оно основывается на представлении сигнала в виде суммы гармонических функций различных частот.
Дискретное преобразование Фурье основано на теории Фурье, которая утверждает, что любой периодический сигнал может быть представлен в виде суммы гармонических компонент различных частот. ДПФ позволяет применить эту теорию к не периодическим сигналам, разбивая их на дискретные отрезки времени и применяя к ним преобразование Фурье. Формула дискретного преобразования Фурье:
Для выполнения дискретное преобразование Фурье необходимо использовать алгоритмы, такие как быстрое преобразование Фурье, которые позволяют выполнить преобразование сигнала быстрее, чем стандартный алгоритм дискретное преобразование Фурье. Быстрое преобразование Фурье использует специальные математические методы для ускорения процесса вычисления, что делает его более эффективным для обработки больших объемов данных. Пример амплитудного спектра синусоидного сигнала представлен в соответствии с рисунком 10.
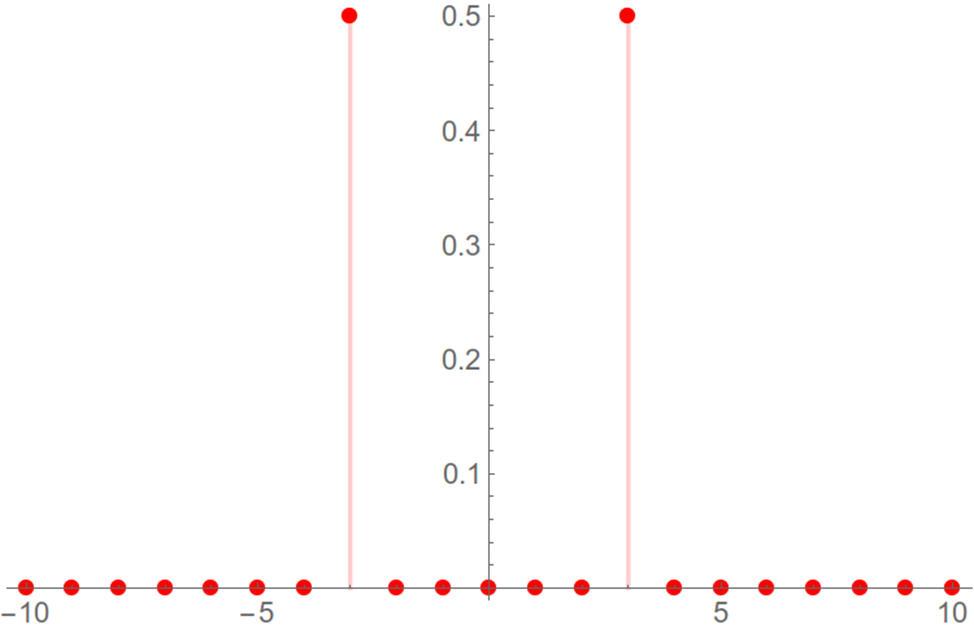
Дискретное преобразование Фурье широко используется в обработке сигналов для анализа спектра частот, выделения определенных частотных компонентов, фильтрации шума и т.д.
Выбор метода анализа частот зависит от требований к точности, скорости обработки и доступности ресурсов вычислительной системы. Для некоторых задач может быть достаточно использовать стандартный алгоритм дискретное преобразование Фурье, в то время как для других задач может потребоваться использование более сложных методов, таких как быстрое преобразование Фурье или другие алгоритмы преобразования сигналов.
После выполнения быстрого преобразования Фурье, полученный результат представляет собой комплексные числа, которые могут быть интерпретированы как амплитуда и фаза сигнала на каждой частоте. Амплитудный спектр показывает, какая часть каждой частоты присутствует в сигнале, а фазовый спектр показывает, как сигнал задерживается на каждой частоте. Эта информация может быть использована для анализа и обработки сигнала, например, для фильтрации шума или выделения определенных частотных компонентов. Соответствие ряда Фурье и преобразования Фурье на примере амплитудного спектра в соответствии с рисунком 11.
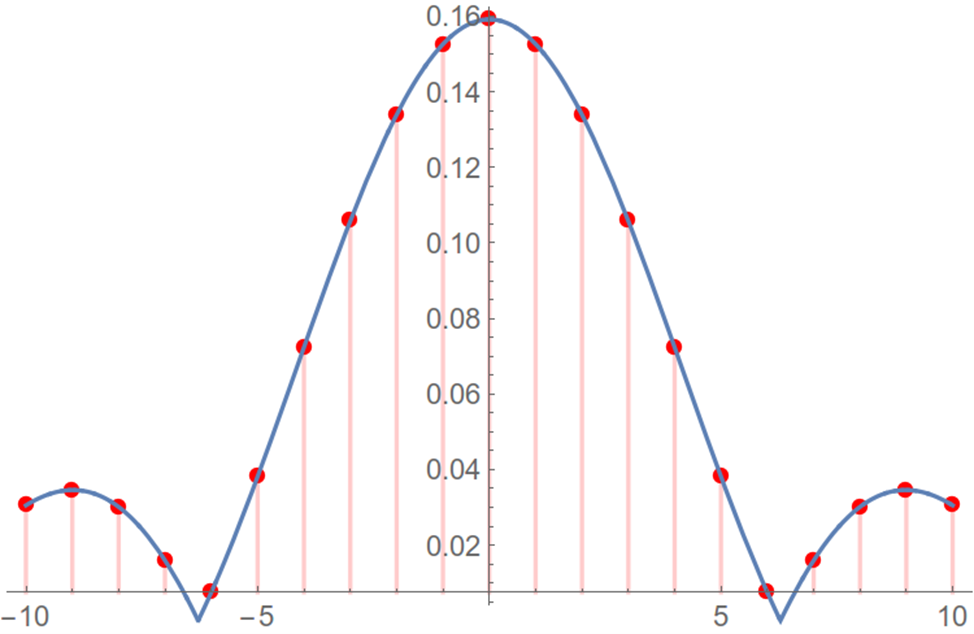
В целом, для анализа ФКГ наиболее эффективным является использование комплексного подхода, который включает в себя несколько алгоритмов. Например, использование фильтрации, сегментации и спектрального анализа может повысить точность диагностики заболеваний сердца по ФКГ.
1.2. Общие принципы работы с файлами данных в формате .csv
CSV (Comma-Separated Values) - это текстовый файл, который содержит табличные данные, разделенные запятыми. Каждая строка файла представляет собой запись таблицы, а каждый столбец - поле записи. Такой формат данных очень удобен для хранения и обмена информацией между различными программами и системам.
Работа с CSV файлами включает в себя чтение, запись и обработку данных. Для работы с CSV файлами используются различные программы и языки программирования. CSV формат данных используется для обмена табличными данными между различными программами и системами, и широко используется в бизнесе, науке, финансах и других областях. CSV файлы содержат данные, которые разделены запятыми или другими символами, например точкой с запятой. Каждая строка файла представляет собой запись в таблице, а каждый столбец - поле записи. Данные в CSV файлах обычно не имеют форматирования и сохраняются в текстовом виде. Для работы с CSV файлами важно знать формат данных, а также понимать, какие символы используются для разделения полей и строк. Кроме того, необходимо уметь читать и записывать данные в CSV файлы, а также обрабатывать их с помощью различных инструментов и программных библиотек. Работа с CSV файлами является важной и неотъемлемой частью работы с табличными данными, и может быть использована в различных об��астях и задачах. При работе с CSV файлами необходимо учитывать особенности локализации, так как в разных странах используются разные символы для разделения полей и строк.
Для удобства работы с CSV файлами многие приложения и сервисы предоставляют возможность импорта и экспорта данных в формате CSV, включая Microsoft Excel, Google Sheets, MySQL и другие. Существуют онлайн-сервисы, такие как CSVLint, которые позволяют проверять корректность формата CSV файлов и исправлять возможные ошибки.
В Python существует специальный модуль csv для работы с CSV файлами, который позволяет читать, записывать и обрабатывать данные в формате CSV.
1.3. Выбор программного обеспечения для реализации алгоритма
Существует несколько языков программирования, с помощью которых можно реализовать алгоритм, с помощью которого можно будет решить поставленную задачу. Было рассмотрено 3 языка основных языка: Python, C++, R.
C++ - это язык программирования, который был разработан в 1983 году Бьярном Страуструпом как расширение языка C. Он предоставляет программистам возможность писать высокопроизводительный код, который может работать на разных платформах. C++ используется для создания приложений, игр, операционных систем и других программных продуктов. Он поддерживает объектно-ориентированное программирование, шаблоны, множественное наследование и другие функции. C++ также известен своей скоростью выполнения и низким уровнем абстракции, что делает его очень популярным среди разработчиков. Анализ данных на C++ возможен, но не является оптимальным выбором из-за низкого уровня абстракции и сложности языка. Для анализа данных обычно используются языки более высокого уровня, такие как Python или R, которые обладают более удобными инструментами для работы с данными и имеют большое количество библиотек для анализа данных. Однако, если необходимо работать с большими объемами данных и требуется высокая производительность, то C++ может быть хорошим выбором [13].
R - язык программирования и среда разработки для статистического анализа данных и создания графиков. Он обладает большим количеством библиотек для работы с данными и позволяет проводить сложные статистические анализы. R широко используется в научных исследованиях, а также в бизнесе для анализа данных и принятия решений.
Python - мощный язык программирования с широким спектром библиотек для анализа данных, простым синтаксисом и поддержкой машинного обучения. Он также используется в веб-разработке [14].
Python широко используется для анализа данных благодаря своим библиотекам, таким как NumPy, Pandas, SciPy, Matplotlib и другим. Эти библиотеки обеспечивают мощные инструменты для работы с массивами данных, статистическими функциями, построением графиков и визуализацией данных.
С помощью Python можно проводить анализ данных, обработку и подготовку данных для машинного обучения, построение моделей машинного обучения и оценку их эффективности. Python также используется для создания приложений для анализа данных и визуализации результатов [15].
Python также имеет большое сообщество пользователей и разработчиков, которые создают новые библиотеки и инструменты для анализа данных, что делает его еще более мощным и гибким для работы с данными [16].
Python и R являются двумя наиболее популярными языками программирования для анализа данных. В целом, выбор между Python и R зависит от конкретных потребностей и задач анализа данных. Если вы работаете с большими объемами данных и нуждаетесь в машинном обучении и глубоком обучении, то Python может быть лучшим выбором. Если же вы работаете с экспериментальными данными и нуждаетесь в большом наборе статистических функций, то R может быть более подходящим выбором. В данном случае был выбран язык Python, так как у меня намного больше знаний инструментов языка python и имеется опыт работы, связанной с данным языком и непосредственно с анализом данных на этом языке.
·
2. Разработка алгоритма обработки фонокардиограммы
На рисунке 12 представлен фрагмент массива данных, хранящихся в файле формата .csv. На рисунке 13 представлен график, построенный на основе массива данных из файла .csv

Алгоритм будет состоять из 5 этапов: центрирование данных относительно 0, усреднение по скользящему окну, удаление фоновых шумов, выделение тонов, этап принятия решения.
Первым этапом алгоритма будет центрирование массива данных относительно нуля. Из графика на рисунке 3 хорошо видно, что в данных имеется постоянная составляющая, кроме того хорошо видно на рисунке 8, что все числа положительные. Звук не предполагает, что у данных будет постоянная составляющая, она связана с особенностями построения регистрирующей аппаратуры, но она совершенно не информативна и поэтому, чтобы предать звуку характерные для него особенности, а именно, наличие как положительных волн, так и отрицательных, производится операция центрирования. Также центрирование необходимо провести для того, чтобы уменьшить ошибки при расчете статистических показателей, сделать данные более понятными и упростить интерпретацию результатов. Для центрирования использовалась следующая формула.
где x_sh(n) – элемент итогового массив данных, x(n) – элемент массива данных.
Реализуем простейший способ выделения огибающей. Это требуется сделать в соответствии со следующей формулой:
где x_t(n) – элемент итогового массива, x(n) – элемент массива данных
Это необходимо сделать для того, чтобы наш алгоритм был более стабильным и точным при обработке данных фонокардиограммы.
В результате мы получаем следующие изменения в массиве данных в соответствии с рисунком 14.
На втором этапе предлагаемого алгоритма необходимо усреднить данные по скользящему окну, таким образом убрать высокие частоты в соответствии с формулой. Это может помочь улучшить качество сигнала или уменьшить влияние выбросов на результаты анализа данных. Необходимо взять сигналы, по ним прогнать данные и понять, что если поменять длину скользящего окна, то результат может быть лучше, в итоге длина скользящего окна w был вычислен в результате метода оптимизация вручную.
В качестве уравнения для фильтрации можно использовать простейшую формулу скользящего среднего.
где w – длина скользящего окна.
В результате мы получаем следующие изменения в массиве данных в соответствии с рисунком 15.
На третьем этапе требуется обработать сигнал таким образом, чтобы можно было в последствии однозначно дифференцировать интервалы, где есть тоны фонокардиограммы и интервалы где их нет (планируется их прировнять к нулю). Для того чтобы отличить интервалы, где есть шум, а где нет, необходимо учитывать стандартное отклонение на всем сигнале и среднее значение массива данных. Требуется вычислить уровень шумоподавления при помощи следующей формулы.
где cutoffValue – уровень шумоподавления, m – среднее значение массива данных, s – стандартное отклонение
Для этого потребуется дополнительный этап разработки алгоритма. Необходимо взять сигналы, по ним прогнать данные и понять, что если поменять коэффициент, то результат может быть лучше, в итоге коэффициент k был вычислен в результате метода оптимизация вручную. Предполагается, что алгоритм будет применен с разными значениями параметров к одним и тем же сигналам и в результате будет видно, какое значение параметра будет являться оптимальным Наилучшим значением k = 3.1
Фильтрация заключается в том, что значению элемента массива, который не удовлетворяет неравенству (5) присваивается значение 0. Данный метод является методом нелинейной фильтрации.
где x – единичное значение из массива данных.
В результате мы получаем следующие изменения в массиве данных в соответствии с рисунком 16. На рисунке видно, что значения, которые не удовлетворили формуле (5), стали равны 0. Также представлен график после удаления шумов в соответствии с рисунком 17

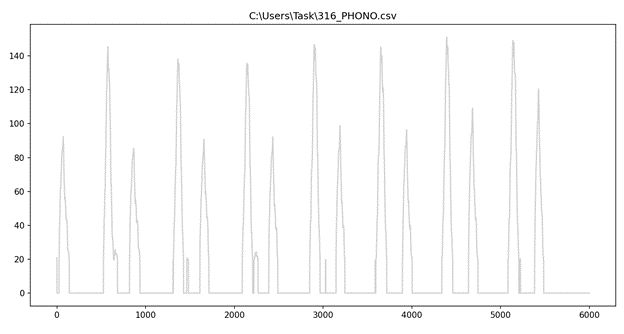
На заключительном этапе нашего алгоритма требуется создать две функции. Первая из которых вычисляет индексы начало и конца каждого из тонов, а вторая вычисляет максимум тона.
Необходимо создать функцию, которая принимает массив данных, среднее значение и пороговое значение, вычисленные на 3 этапе. Функция находит левые и правые края каждого тона по следующим условиям: для краев левого тона – если встречается значение элемента массива данных не равное нулю, то данный элемент обозначается как начало тона и правого края тона – если встречается значение элемента равного нулю, то этот элемент обозначается как конец тона. Функция возвращает индексы левого и правого краев. Таким образом вычисляется начало тона и конец тона, это левый и правый индексы краев.
Требуется создать функцию, которая принимает массив данных, начальный и конечный индексы. Функция находит индекс максимального значения в определенном промежутке и возвращает его. Таком образом вычисляется точка максимальной амплитуда тона.
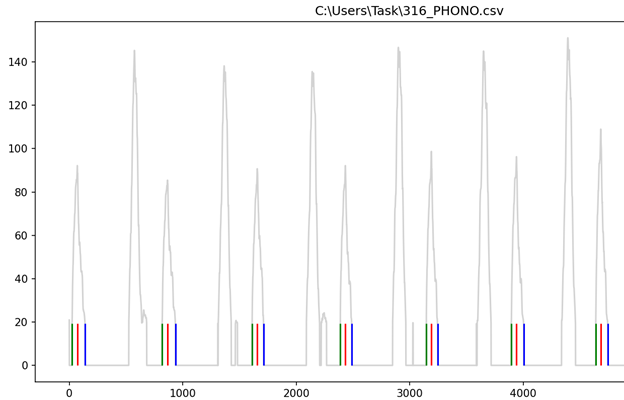
Результат алгоритма представлен двумя вариантами. На графике выделены начало (зеленый цвет), точка максимальной амплитуды (красный цвет) и окончание (синий цвет) в соответствии с рисунком 18.
Список списков, где каждый список выглядит как [t1, t2, t3], где t1 - начало, t2 - точка максимальной амплитуды, t3 – окончание для каждого из сердечных циклов в соответствии с рисунком 19.

3. Программная реализация предложенного алгоритма обработки
Программная реализация предложенного алгоритма предполагает написания решения поставленной задачи. Необходимо представить таблицу с обозначениями переменных из кода на языке python в соответствии с таблицей 1.
Таблица 1 – Обозначение переменных
Переменная | Обозначение переменной |
array | Список, в котором содержатся данные из файла |
st | Стандартное отклонение |
maxVal | Максимальное значение списка array |
med | Среднее значение списка array |
cutoffValue | Уровень шумоподавления |
threshold | Количество точек, которые должны идти прямо, чтобы считаться началом и концом тона |
toneMinLen | Минимальная длина тона |
windowLength | Размер скользящего окна |
leftEdges | Левый край тона |
rightEdges | Правый край тона |
peak | Пик тона |
tones | Результирующий список |
first_tones | Первый тон |
shift | Нормализуемое значение списка array |
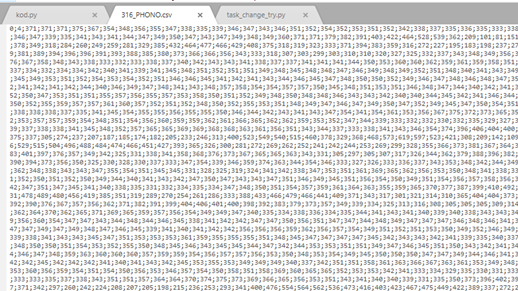
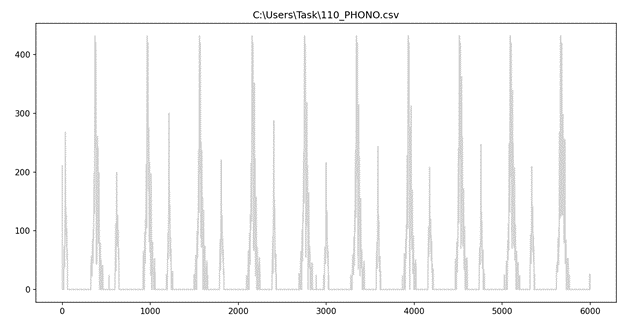
Дан список файлов в формате .csv, файлы хранят данные медицинских исследований. Пример того, как выглядит файл в формате .csv в соответствии с рисунком 20. В качестве конкретного примера здесь и далее берем файла под названием " 110_PHONO.csv ".
С помощью инструментов языка python [17], достаем и визуализируем данные в соответствии с листингом 1, из файла в виде графика в соответствии с рисунком 21.
Листинг 1 – Визуализация данных из файла в формате .csv
from matplotlib import pyplot from numpy import median, short, mean, sqrt, var import os dir_name = 'C:\\Users\\Task\\' test = os.listdir(dir_name) test = list(test) for i in test: with open(dir_name+str(i), newline='') as data: array = list(map(lambda x: int(x),data.read().split(";"))) pyplot.figure(figsize=(10,3)) pyplot.title(dir_name+str(i)) pyplot.plot(array,color="lightgray")
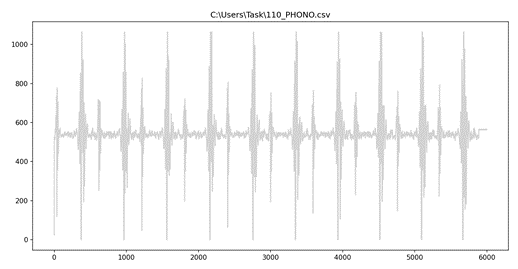
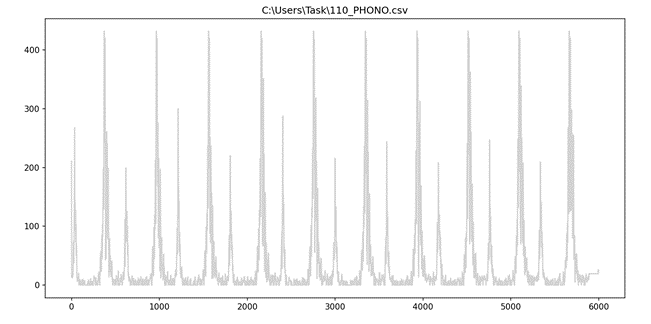
Далее необходимо пишем программу, которая осуществляет центрирование все значения относительно 0 в соответствии с формулой 1. Результат в соответствии с рисунком 22. Реализация центрирования на python в соответствии с листингом 2. На данном этапе все довольно просто, поэтому примеры каких-то неудачных действий или обработки данных нет, все получилось достаточно быстро и с первой попытки.
Листинг 2 – Центрирование данных относительно 0
def normalize(x,avg): shift = x - avg if shift >= 0: return shift else : return –shift med = mean(array) array = list(map(lambda x: normalize(x,med),array)) # нормализуем прочитанный #массив
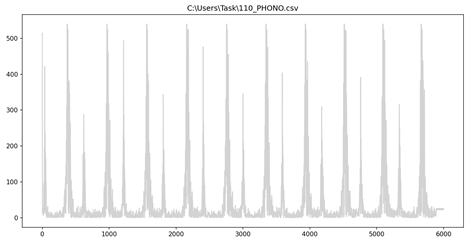
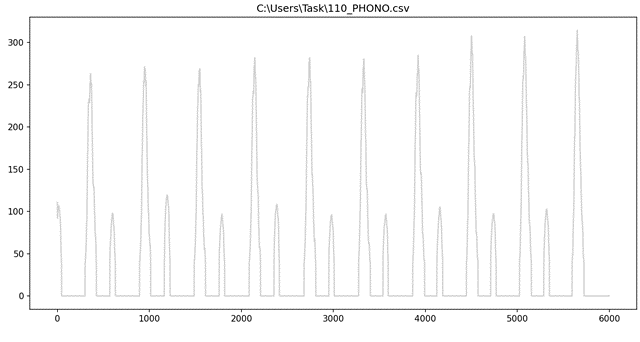
Необходимо усреднить по скользящему окну, таким образом убрать высокие частоты в соответствии с формулой (4). Результат в соответствии с рисунком 24. Реализация на языке python в соответствии с листингом 3. Изначально производилась попытка присвоить скользящему окну значение 5 в соответствии с рисунком 23, но в итоге значение 50 оказалось оптимальным.
Листинг 3 – Убираем высокие частоты
for idx in range(len(array)-windowLength): #усреднение по скользящему окну #размера windowLength - убираем высокие частоты array[idx] = sum(array[idx:idx+windowLength-1])/windowLength
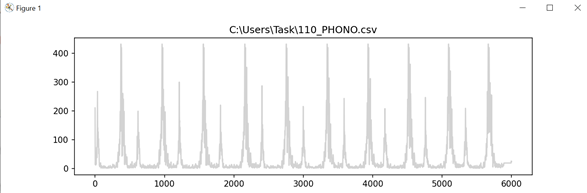
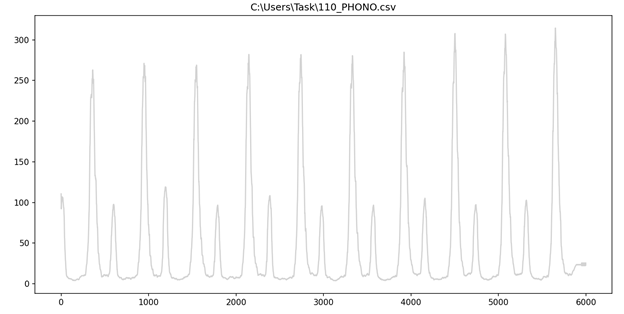
Требуется выполнить выделение интервалов компоненты фонокардиограммы в соответствии с формулой (5). В ходе поиска оптимального значения коэффициента k, в качестве примера, были выведены два графика, на которых фоновые шумы удаляются неправильно в соответствии с рисунками 25 и 26. Оптимальным значением коэффициента оказалось значение 3.1, график без фоновых шумов представлен в соответствии с рисунком 27. Также необходимо присвоить значение 0 всем элементам массива, которые не удовлетворяют неравенству в соответствии с формулой (5).
Реализация на языке python в соответствии с листингом 4. Последствия неправильного удаления шумов и какие ошибки это за собой это может повлечь отображено на рисунке 28. Из-за того, что фоновые шумы были удалены неправильно, часть меток, характеризующих начало (зеленый цвет), точка максимальной амплитуды (красный цвет) и окончание (синий цвет) были установлены некорректно.
Листинг 4 – Выделение интервалов компоненты фонокардиограммы
def cutOff(x, threshold): if x >= threshold: return x else : return 0 cutoffValue = (med + st)/3.1 #уровень шумоподавления array = list(map(lambda x: cutOff(x,cutoffValue),array)) # убираем фоновые шумы #из нормализованного массива
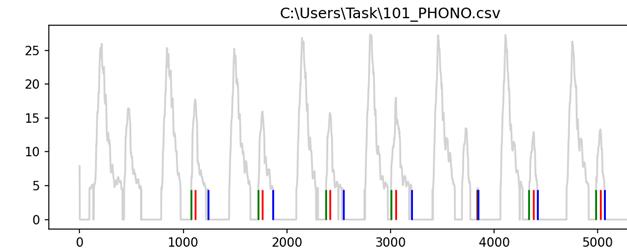
Далее необходимо выделить тоны и вывести их на экран. Требуется сделать это двумя способами, первый способ - записать в виде списка списков, каждый список выглядит как [t1, t2, t3], где t1 - начало, t2 - точка максимальной амплитуды, t3 – окончание для каждого из сердечных циклов в соответствии с рисунком 29. А также требуется визуализировать полученные результаты на графике в соответствии с рисунком 30. Реализация на языке python в соответствии с листингом 5. При решении данного этапа алгоритма также не возникло никаких трудностей, так как идея была одна, она была успешно реализована и представлена.
Листинг 5 – Выделение тонов
#находим индекс максимального значения в определенном промежутке def findPeakIndex(array, start, end): interval = array[start:end] maxValue = max(interval) return array.index(maxValue,start-1,end+1) # оставляем только 1 тон def first_tone(array, first_tones): b= [] c = [] def split(arr, size): arrs = [] while len(arr) > size: pice = arr[:size] arrs.append(pice) arr = arr[size:] arrs.append(arr) return arrs first_tones = split(first_tones, 3) for i in range(1, len(first_tones)): b.append(first_tones[i][0] - first_tones[i-1][2]) for i in range(1, len(first_tones)): for j in range(1, len(b)): if i == j: if sum(array[first_tones[i][0]:first_tones[i][2]+1])>sum(array[first_tones[i-1][0]:first_tones[i-1][2]+1]) and b[j]<b[j-1]: c.append(first_tones[i-1]) return c # собираем данные в класс Tone, упаковываем def makeTones(leftEdges,rightEdges,minLenforTone): tones = [] first_tones = [] if(rightEdges[0] < leftEdges[0]):# если у нас есть правый край, но у него нет парного левого края - удаляем его rightEdges.pop(0) if leftEdges[-1] > leftEdges[-1]: # если есть левый край, но нет парного правого - удаляем leftEdges.pop(len(leftEdges)-1) for i in range(min(len(leftEdges),len(rightEdges))): # для каждого левого и правого края создаем объект Tone, и в промежутке этих краев находим значение максимальной амплитуды if(rightEdges[i] - leftEdges[i] > minLenforTone): peak = findPeakIndex(array,leftEdges[i],rightEdges[i]) first_tones.append(leftEdges[i]) first_tones.append(peak) first_tones.append(rightEdges[i]) first_tones = first_tone(array, first_tones) for i in range(len(first_tones)): tones.append(Tone(first_tones[i][0],first_tones[i][1],first_tones[i][2])) return tones LeftEdges, RightEdges = findEdgesNormal(array, threshold) # находим края tones = makeTones(LeftEdges,RightEdges,toneMinLen) # по данным о краях создаем тоны #добавляем вертикальные полосы, отображающие тон pyplot.vlines(x=[l.LeftPoint for l in tones],color="green",ymin=0,ymax=cutoffValue) #начало тона pyplot.vlines(x=[r.RightPoint for r in tones],color="red",ymin=0,ymax=cutoffValue) # конец тона pyplot.vlines(x=[p.Peak for p in tones],color="blue",ymin=0,ymax = cutoffValue)# пик тона pyplot.show()

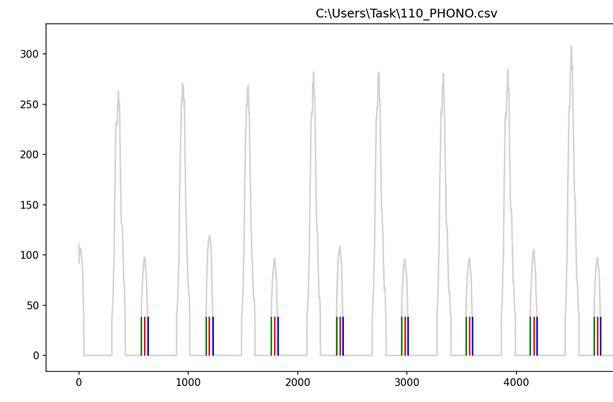
Созданный алгоритм был рассмотрен на примере одного набора данных. Ниже представлены результаты работы алгоритма с другими данными, которые находятся в других файлах. Успешная реализация алгоритма в соответствии с рисунками 31, 32, 33. Начало (зеленый цвет), точка максимальной амплитуды (красный цвет) и окончание (синий цвет).
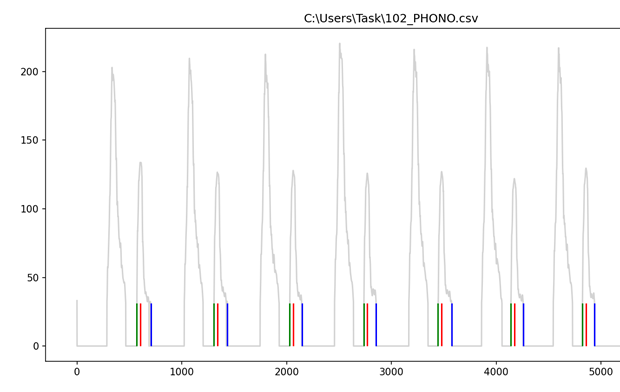
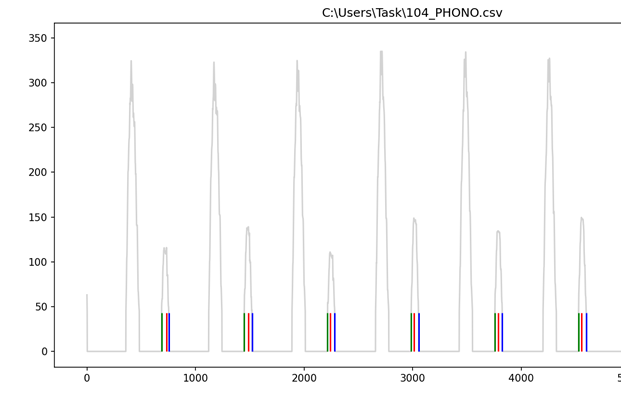
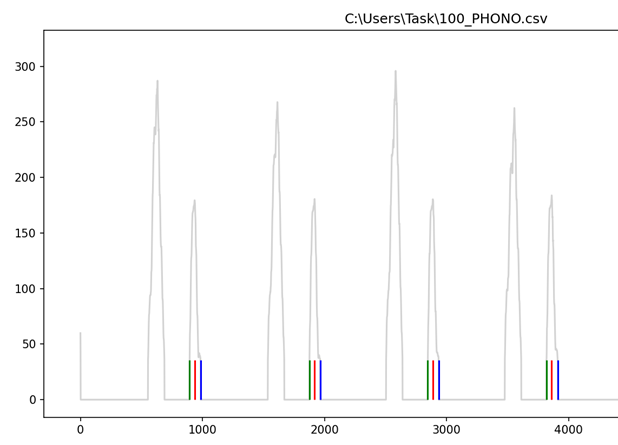
Код представлен в соответствии с приложением А.
ЗАКЛЮЧЕНИЕ
В выпускной квалификационной работе был поэтапно реализован алгоритм, при помощи которого решается поставленная задача, программно реализован на языке python и получен необходимый результат.
В ходе разработки алгоритма анализа данных фонокардиограммы были успешно выполнены следующие этапы: центрирование данных относительно 0, усреднение по скользящему окну, удаление фоновых шумов, выделение тонов, этап принятия решения.
В ходе последовательного выполнения этапов алгоритма были изучены и применены следующие навыки. Чтобы предать звуку характерные для него особенности, а именно, наличие как положительных волн, так и отрицательных была выполнена операция центрирования. затем было выполнено усреднение данных по скользящему окну, таким образом удалось убрать высокие частоты при помощи соответствующей формулы, ради которой требовалось с помощью оптимизации вручную вычислить длину скользящего окна, которым являлся коэффициент w. Затем был реализован простейший способ выделения огибающей, это необходимо было сделать для того, чтобы наш алгоритм был более стабильным и точным при обработке данных фонокардиограммы. Также было выполнено усреднение данных по скользящему окну, таким образом удалось убрать высокие частоты при помощи соответствующей формулы, в которой требовалось с помощью оптимизации вручную вычислить длину скользящего окна, которым являлся коэффициент w. Далее было выполнено выделение интервалов компоненты фонокардиограммы при помощи сравнения каждого элемента массива данных с уровнем шумоподавления, который был вычислен при помощи специальной формулы, в которой использовались среднее значение массива данных, стандартное отклонение и коэффициент k, который был вычислен при помощи оптимизации вручную, данный метод является методом нелинейной фильтрации. В результате были найдены при помощи двух функций и выделены начало тона, конец тона, максимум амплитуды и представлены двумя разными способами, с помощью списка списков и отмечены разными цветами на графике.
Алгоритм правильно работает с 240 файлами из 318 возможных, то есть выполняет поставленную задачу примерно в 75% случаев.
После грамотной реализации представленного алгоритма, можно ставить задачу спектрального анализа полученных данных, с целью анализа частот этих самых частот, но это уже не входит в цели работы.
СПИСОК ЛИТЕРАТУРЫ
1. Григорьев Е.Б., Красичков А.С. Программа оценки динамики изменения тонов и шумов сердца. Vol. 4. P. 24–27.
2. Кумар Прашант et al. Устройство и способ обработки сигналов фонокардиограммы. 2010. Vol. 2. P. 19–21.
3. Ракицкий Ю.С. Импорт и экспорт ролевой политики безопасности в СУБД Oracle // Математические Структуры И Моделирование. 2018. № 4 (48).
4. Bachevskiy S.V. A software-hardware solution for analysis of phono-cardiograms. 2019. Vol. 3. P. 121–125.
5. Сепери Амир А., Гаребаги Араш. Способ И Устройство Для Определения Частотного Диапазона Шума. 2014. Vol. 1, № 1. P. 13–17.
6. Kalaivani V. Diagnosis of arrhythmia dideases using heart sounds and acg signals. 2014. Vol. 1. P. 12–15.
7. Никитин В.М., Муромцев В.В., Анохин Д.А. Программно-Аппаратный Комплекс Для Фонокардиографических Исследований // Научные Ведомости Белгородского Государственного Университета Серия Экономика Информатика. 2012. № 13 (132).
8. Tomas Bozo. Graphics representations and frequency parametrs of heart sounds signals // Data science. 2018. Vol. 3, № 1. P. 7–8.
9. Бурсов А.И. Применение искусственного интеллекта для анализа медицинских данных // Альманах Клинической Медицины. Государственное учреждение Московский областной научно-исследовательский клинический институт имени М. Ф. Владимирского, 2019. Vol. 47, № 7. P. 630–633.
10. Klimiankov Y.I. An operating system bootstrapping package for IBM PC compatible computer system. 2019. Vol. 6, № 11.
11. Юзбашев З.Ю., Майскова Е.А. Методы исследования сердца, основанные на регистрации низкочастотных колебаний прекордиальной зоны, их диагностические возможности и перспективы // Исследования сердца в нашем мире. 2017. Vol. 1.
12. Шабаев М.Б., Матыгов М.М. Сравнение SEO и GOOGLE ADS // Тенденции Развития Науки И Образования. 2020. № 68–1.
13. Фокин Р.Р., Атоян А.А., Абиссова М.А. Вопросы структурирования алгоритмов и программ С++ при изучении студентами информатики // Научный Альманах. 2022. № 7-1 (93).
14. Ламонина Л.В., Смирнова О.Б., Сорокин А.А. О программировании на языке Python. Омский государственный аграрный университет имени П.А. Столыпина, 2022. P. 445–453.
15. Открытый курс машинного обучения. Тема 9. Анализ временных рядов с помощью Python [Electronic resource] // Хабр. 2017. URL: https://habr.com/ru/company/ods/blog/327242/ (accessed: 21.02.2023).
16. Пирматов А.З., Камалов С.С. Объектно-ориентированное программирование на языке Python // Вестник Журнал Жалал-Абадского Госудраственного Университета. 2022. № 4 (53). P. 22–28.
17. Ельсуков Д.А. Python - Язык программирования // Экономика И Социум. 2021. № 11-1 (90). P. 982–985.
ПРИЛОЖЕНИЕ А
from matplotlib import pyplot from numpy import median, short, mean, sqrt, var import os class Tone(object): def __init__(self,left,right,peak): self.LeftPoint = left self.RightPoint = right self.Peak = peak # KAA: Нормализуем значение. def normalize(x,avg): shift = x - avg if shift >= 0: return shift else : return -shift def cutOff(x, threshold): if x >= threshold: return x else : return 0 #находим левые и правые края по следующим условиям # для левого края - слева определенное кол-во точек равны медианному, а следующая точка отличается # для правого края - справа определенное кол-во точек равны медианному, а предыдущая точка отличается def findEdges(array,avg,threshold): LeftEdges = [] RightEdges = [] for i in range(threshold,len(array)-threshold): if isLeftStraight(array,avg,i,threshold) and array[i+1] != avg: LeftEdges.append(i) if isRightStraight(array,avg,i,threshold) and array[i-1] != avg: RightEdges.append(i) return LeftEdges,RightEdges #находим левые и правые края по следующим условиям # для левого края - слева определенное кол-во точек равны 0, а следующая точка отличается # для правого края - справа определенное кол-во точек равны 0, а предыдущая точка отличается def findEdgesNormal(array, threshold): LeftEdges = [] RightEdges = [] for i in range(threshold,len(array)-threshold): if isLeftStraight(array,0,i,threshold) and array[i+1] != 0: LeftEdges.append(i) if isRightStraight(array,0,i,threshold) and array[i-1] != 0: RightEdges.append(i) return LeftEdges,RightEdges def isLeftStraight(array,avg,index,threshold): isleftStr = True for i in range(threshold): isleftStr = isleftStr and array[index-i] == avg if not isleftStr: return False return isleftStr; def isRightStraight(array,avg,index,threshold): isrightStr = True for i in range(threshold): isrightStr = isrightStr and array[index+i] == avg if not isrightStr: return False return isrightStr; #находим индекс максимального значения в определенном промежутке def findPeakIndex(array, start, end): interval = array[start:end] maxValue = max(interval) return array.index(maxValue,start-1,end+1) # оставляем только 1 тон def first_tone(array, first_tones): b= [] c = [] def split(arr, size): arrs = [] while len(arr) > size: pice = arr[:size] arrs.append(pice) arr = arr[size:] arrs.append(arr) return arrs first_tones = split(first_tones, 3) for i in range(1, len(first_tones)): b.append(first_tones[i][0] - first_tones[i-1][2]) for i in range(1, len(first_tones)): for j in range(1, len(b)): if i == j: if sum(array[first_tones[i][0]:first_tones[i][2]+1])>sum(array[first_tones[i-1][0]:first_tones[i-1][2]+1]) and b[j]<b[j-1]: c.append(first_tones[i-1]) print(c) return c # собираем данные в класс Tone, упаковываем def makeTones(leftEdges,rightEdges,minLenforTone): tones = [] first_tones = [] if(rightEdges[0] < leftEdges[0]):# если у нас есть правый край, но у него нет парного левого края - удаляем его rightEdges.pop(0) if leftEdges[-1] > leftEdges[-1]: # если есть левый край, но нет парного правого - удаляем leftEdges.pop(len(leftEdges)-1) for i in range(min(len(leftEdges),len(rightEdges))): # для каждого левого и правого края создаем объект Tone, и в промежутке этих краев находим значение максимальной амплитуды if(rightEdges[i] - leftEdges[i] > minLenforTone): peak = findPeakIndex(array,leftEdges[i],rightEdges[i]) first_tones.append(leftEdges[i]) first_tones.append(peak) first_tones.append(rightEdges[i]) first_tones = first_tone(array, first_tones) for i in range(len(first_tones)): tones.append(Tone(first_tones[i][0],first_tones[i][1],first_tones[i][2])) return tones # собираем данные в класс Tone, упаковываем def makeTonesOld(leftEdges,rightEdges,minLenforTone): tones = [] if(rightEdges[0] < leftEdges[0]):# если у нас есть правый край, но у него нет парного левого края - удаляем его rightEdges.pop(0) if leftEdges[-1] > leftEdges[-1]: # если есть левый край, но нет парного правого - удаляем leftEdges.pop(len(leftEdges)-1) for i in range(min(len(leftEdges),len(rightEdges))): # для каждого левого и правого края создаем объект Tone, и в промежутке этих краев находим значение максимальной амплитуды if(rightEdges[i] - leftEdges[i] > minLenforTone): peak = findPeakIndex(array,leftEdges[i],rightEdges[i]) tones.append(Tone(leftEdges[i],rightEdges[i],peak)) return tones dir_name = 'C:\\Users\\Task\\' test = os.listdir(dir_name) test = list(test) for i in test: with open(dir_name+i, newline='') as data: array = list(map(lambda x: int(x),data.read().split(";"))) #KAA: med = mean(array) threshold = 20 #сколько точек должны идти прямо, чтобы считаться началом или концом тона toneMinLen = 5 #какая минимальная длина должна быть у реального тона(нужна чтобы отсечь фейковые всплески) #KAA: array = list(map(lambda x: normalize(x,med),array)) # нормал��зуем прочитанный массив windowLength = 50 for idx in range(len(array)-windowLength): #усреднение по скользящему окну размера windowLength - убираем высокие частоты array[idx] = sum(array[idx:idx+windowLength-1])/windowLength maxVal = max(array) med = mean(array) st = sqrt(var(array)) # стандартное отклонение cutoffValue = (med + st)/3.1 #уровень шумоподавления array = list(map(lambda x: cutOff(x,cutoffValue),array)) # убираем фоновые шумы из нормализованного массива LeftEdges, RightEdges = findEdgesNormal(array, threshold) # находим края tones = makeTones(LeftEdges,RightEdges,toneMinLen) # по данным о краях создаем тоны #рисуем основной график pyplot.figure(figsize=(10,3)) pyplot.title(dir_name+i) pyplot.plot(array,color="lightgray"); #добавляем вертикальные полосы, отображающие тон pyplot.vlines(x=[l.LeftPoint for l in tones],color="green",ymin=0,ymax=cutoffValue) #начало тона pyplot.vlines(x=[r.RightPoint for r in tones],color="red",ymin=0,ymax=cutoffValue) # конец тона pyplot.vlines(x=[p.Peak for p in tones],color="blue",ymin=0,ymax = cutoffValue)# пик тона pyplot.show()
