На хабре уже пару раз упоминался дизеринг, но в довольно узком ключе. Здесь, я хоть и буду делать упор на применение дизеринга в графике, я хочу продемонстрировать недооценённость некоторых его алгоритмов.
Терминология
Вкратце, для тех кто в танке, что такое дизеринг. Это намеренное добавление шума, направленное на уменьшение ошибок квантизации(округления). Вы, конечно, можете использовать его как артистический приём (что уже описывалось на хабре), но в основном это довольно утилитарная вещь, которая применяется куда бы вы ни пошли в графике.
Пример



Есть много видов дизеринга, но я буду рассматривать только те, которые не опираются на предыдущие значения при рассмотрении текущего. То есть GPU friendly алгоритмы.
При этом просто добавление белого шума не позволяет сохранить большую часть информации.
Изображение сжато только до двух цветов: только черный и только белый. Если пиксель шума имеет меньшее значение (темнее), чем пиксель изображения, мы возвращаем черный пиксель, в противном случае мы возвращаем белый пиксель.


Здесь на свет выходят известные в математике последовательности с низким расхождением. По сути это функции со следующим видом:
Где натуральное число, индекс,
вектор (точка) в
-мерном пространстве, а
детерминированная функция.
Они позволяют примерно равномерно покрыть некий диапазон значений, при этом избегая паттернов, которые могут резонировать с исходными данными, как если бы мы просто взяли одинаковые промежутки диапазона. Так, в математике такие последовательности широко применяются в методах квази-Монте-Карло для численного интегрирования. При их применении ключевая идея состоит в том, что точки, выбранные из такой последовательности, равномерно покрывают область интегрирования гораздо эффективнее, чем набор независимых случайных точек.
Сетка с низким расхождением (LDG) (которые можно считать особым случаем последовательностей с низким расхождением) — это структурированное детерминистическое расположение значений в многомерном пространстве, индексированное целочисленными координатами, предназначенное для поддержания равномерного распределения (низкого расхождения) по всей области. Они принимают на вход координаты и возвращают скалярное значение. Они не имеют какой-либо стартовой точки, поскольку также хорошо работают с негативными координатами. Последовательности же являются частью некой прогрессии, и большиство из них плохо масштабируются в более высокие измерения. В данном случае будут рассматриваться двумерные сетки.
Также упоминания стоит синий шум. Синий шум называется синим шумом, потому что он содержит большее количество высоких частот и меньшее количество низких частот. Это то же самое, что и синий свет, который содержит более высокочастотный (синий) свет. При этом эти частоты примерно равномерно распределены по диапазону. Таким образом, в то время как рисунок синего шума выглядит как случайные точки, расположенные на одинаковом расстоянии друг от друга, рисунок белого шума выглядит как чисто случайные точки, состоящие из больших скоплений и больших открытых промежутков.
Пример

Из-за своих свойств синий шум довольно сложно генерировать, из-за чего в графике (и многих других сферах) его предпочитают заранее просчитать, а затем при помощи некоторых приблежений применять. Например, при помощи этого метода даже из текстуры 32х32 можно стабильно получать наборы значений крайне близкие по своим свойствам к оригинальному синему шуму.
Конкретный пример, Interleaved Gradient Noise
Хотя синий шум крайне хорош по своим свойствам, его применение означает семплирование текстуры, чего в шейдерах нужно избегать, если это возможно. Практически любые математические операции будут быстрее, чем семплирование.
Начнём с самого популярного метода: IGN, или же Interleaved Gradient Noise. Он был предложен в 2014 году by Jorge Jimenez из Activision.
Примеры и сравнение распределения значений для области 16х16


Для сравнения приведён ещё паттерн Bayer. Хоть он идеально покрывает диапазон, вы легко можете видеть паттерн, который резонирует с исходными данными.
Он призван был решать конкретную проблему: если сильно упрощать, TAA алгоритмы совмещают предыдущий кадр с текущим. При этом совмещении, у нового кадра может быть новая информация, которой не было в предыдущем кадре. Если при проекции предыдущего кадра с матрицей движения не было валидной информации (из‑за движения или джиттеринга проекции), то семплируется блок соседних пикселей 3×3, чтобы найти наиболее похожую информацию на текущую. Это повышает шансы получить валидный результат.
Когда TAA делает выборку в районе 3×3, цель состоит в том, чтобы получить представление о том, какие возможные цвета пиксель должен принимать, основываясь на других пикселях в локальной области. Чем точнее это соседство представляет возможные значения пикселей в этой локальной области, тем точнее будет отклонение невалидных пикселей из истории истории. IGN делает локальную область более точной, представляя полный набор возможностей в небольших окрестностях пикселей.
К примеру, у нас есть полупрозрачный объект использующий альфа клиппинг (то есть, отбрасывающий часть пикселей, и рендерящий часть пикселей как полностью непрозрачные), у которого прозрачность равно 1/9, то в любой области 3×3 мы ожидаем, что как минимум один пиксель такого объекта будет включён как возможный в TAA. Если мы используем для такой задачи белый шум, то в итоге будут некоторый области с множестом отброшенных пикселей, и области с множеством не отброшенных, что сломает эффект полупрозрачности.
Если вы захотите сесть и переизобрести IGN, то вот как будут звучать условия задачи: «Для каждого блока 9×9 пикселей на бесконечной текстуре должны быть значения ~ от 0/9 до 8/9». На данный момент, вы буквально описали судоку. Если ещё добавить «Это правило также должно быть верно для пересекающихся блоков», вы описали обобщённое судоку. Однако, в этой задаче слишком много конфликтующих ситуаций, и она не разрешима. Способ обойти эту проблему — немного сместить числа по пространству, чтобы она была в основном решена, а ошибка несовершенного решения была распределена по пространству. На этом этапе вы достигли того, как работает IGN.
HLSL Код
float IGN(int pixelX, int pixelY, int frame)
{
const float3 magic = float3(0.06711056, 0.00583715, 52.9829189);
const float frameOffset = 5.588238f;
frame = frame % 64; // Periodically reset frame to avoid numerical issues
float x = float(pixelX) + frameOffset * float(frame);
float y = float(pixelY) + frameOffset * float(frame);
return frac(magic.z * frac(magic.x * x + magic.y * y));
}Jorge Jimenez потратил полный 8-часовой рабочий день, вручную подбирая подходящие «магические числа» для этого алгоритма.
С IGN каждая область пикселей 3×3 (даже перекрывающиеся) имеет набор значений с низким расхождением, поэтому можно ожидать, что из каждой области 3×3 из 9 пикселей этот 1 пиксель всегда переживет альфа‑клиппинг. Вот как IGN улучшает рендеринг в TAA.
Синий шум частично имеет это свойство, но не так гарантированно, как IGN. Bayer ordered, похоже, имеет это свойство в горизонтальной и вертикальной плоскости, но не в диагональной, а также выглядит более искусственно.
Пример

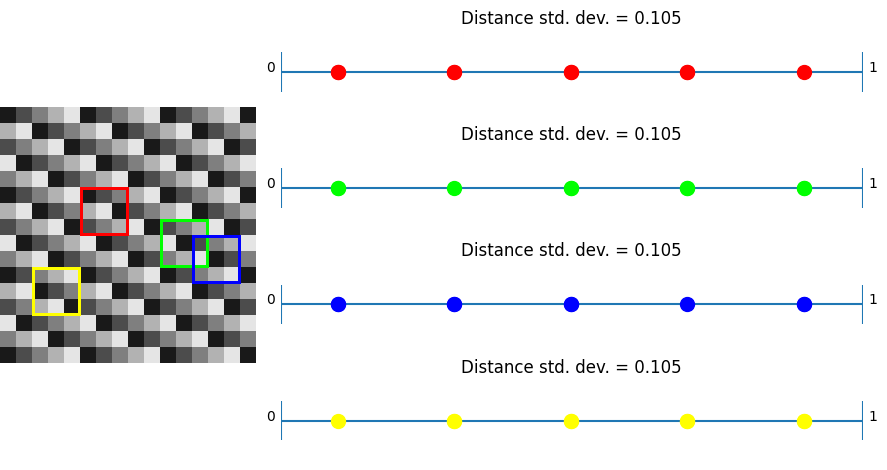
Давайте возьмём несколько блоков пикселей, и посмотрим на расстояния между значениями этих пикселей, чтобы лучше понять как работает этот шум. IGN имеет очень низкое стандартное отклонение.

Пустоты и скопления белого шума ведут к большим отклонениям между значениями

Синий шум имеет намного лучшую картину, но она гораздо хуже, чем IGN.

В общем, если вам нужны попиксельно уникальные значения, которые в некоторой области будут корректно отображать общую картину, IGN ваш хороший друг.
R2 LDG
Этот метод был впервые предложен в 2018 by Martin Roberts в его статье The Unreasonable Effectiveness of Quasirandom Sequences. последовательность является последовательностью Кронекера, использующая золотое сечение. Это позволяет ей быть одним из лучших вариантов для одномерных методов квазислучайной интеграции Монте-Карло (см статью).
Благодаря использованию золотого сечения этот алгоритм обладает многими удивительными математическими свойствами, однако, поскольку они уже подробно описаны в первоисточнике, не буду вдаваться в них в этой обзорной статье.
Для 1d алгоритм выглядит так:
g = 1.6180339887498948482
a1 = 1.0/g
x[n] = (0.5+a1*n) %1 Для 2d алгоритм будет выглядеть так:
g = 1.32471795724474602596
a1 = 1.0/g
a2 = 1.0/(g*g)
x[n] = (0.5+a1*n) %1
y[n] = (0.5+a2*n) %1 Для любого набора измерений будет равна:
(См https://ru.wikipedia.org/wiki/Пластическое_число)
Для 1d это золотое сечение (1.6180339887498948482), для 2d это пластическое число (1.32471795724474602596), а для 3d оно записано как [OEIS A079398] в инциклопедии бесконечных последовательностей.
HLSL код для 2d
float r_dither(float2 pos, float t)
{
const float2 magic = float2(0.75487766624669276, 0.569840290998);
return frac(dot(pos, magic) + t);
}Значения захардкожены в целях производительности.
Пример в дизеринге

Для получения дизеринга IGN требуется 3 умножения с плавающей точкой и два оператора %1, тогда как предыдущий код показывает, что мы можем получить схожий дизеринг всего с 2 умножениями с плавающей точкой и одной операцией %1. Что еще важнее, указанная выше статья дает более четкое математическое понимание того, почему маска дизеринга этой формы настолько эффективна, если не оптимальна.
Всё это делаеталгоритм хорошим вариантом сетки с низким расхождением общего назначения.
Однако, в частном случае зоны 3х3, дизеринг даёт большее стандартное отклонение, чем IGN.

Plus LDG
В некоторых реализациях TAA вместо того, чтобы брать полную область 3х3 вокруг пикселя, будут сэмплироваться только 4 соседа по ос��м, создавая плюсовую форму (+) сэмплирования. Это может снизить требования к пропускной способности памяти, поскольку сокращает сэмплирование окрестностей вдвое, с 8 сэмплов до 4.
Поэтому в 2022 году был предложен Plus LDG by Alan Wolf. Он специально создан для областей + формы.
HLSL код
float PlusShapedLDG(int pixelX, int pixelY)
{
return fmod(((float(pixelX) + 3 * float(pixelY))/5) + 1/10, 1);
}Пример

Мы получааем регулярную сетку значений, где каждая плюсовая фигура имеет все значения ~ 0/5, 1/5, 2/5, 3/5, 4/5. Каждая плюсовая фигура, включая перекрывающиеся. Это даёт наиболее точное представление возможных значений для этого пикселя.
Тесты с альфа клиппингом
Чем ближе значение к целевому, тем лучше.




Стоит упомянуть, что процент пикселей белого шума, которые выживают в альфа-тесте, довольно сильно колеблется по сравнению с фактическим значением прозрачности. Это фактически делает пиксели более непрозрачными или более прозрачными, чем они должны быть, что вызывает проблемы при фильтрации в пространстве и/или во времени. Это в дополнение к тому, как белый шум слипается и оставляет дыры, что затрудняет фильтрацию, чем более равномерно распределенные точки.
Еще одна вещь, на которую стоит обратить внимание, заключается в том, что Plus LDG ОЧЕНЬ неверен при 10% и 30%, но очень хорош при 20% и 40%. Причина этого в том, как шум в форме плюса дискретизируется на 1/5. У других шумов есть все значения (от 0 до 255), что означает, что они лучше работают при произвольных непрозрачностях.
Со всеми шумами, кроме Plus LDG, по мере плавного увеличения непрозрачности пиксели начнут медленно появляться. С Plus LDG, по мере того как вы плавно увеличиваете непрозрачность, пиксели будут появляться большими группами, а не по одному. Однако, если в коде вместо 1/10 добавлять случайные значения из синего шума от 0 до 1/5, то порядок можно разбить, при этом сохраняя правильное среднее значение.
В области 3х3 Plus LDG показывает себя хуже чем IGN или . Что неудивительно, ведь он создан для использования в другом контексте.
Однако, при анализе региона в виде +:






В этом тесте, белый шум показывает наихудшие результаты, как обычно. Байер и синий шум тоже не очень хороши.
Теперь, в отличие от последнего теста, где IGN показывал результат лучше , мы видим, что
победил IGN. Это снова показывает, что
хорош в «для общего применения», когда IGN оптимизирован всего лишь для блоков 3×3.
Наконец, мы видим, что Plus LDG здесь работает лучше всего — в ситуации, для которой он был оптимизирован, что неудивительно. Любая рандомизация, добавленная к этому шуму, чтобы помочь разбить артефакты квантования, приведет к тому, что этот конкретный тест будет иметь большее стандартное отклонение. При использовании хорошего шума (например, синего шума) стандартное отклонение может увеличиться лишь немного. Небольшое увеличение стандартного отклонения, вероятно, улучшит результаты в целом при использовании этого шума. В конце концов, цель последовательностей с низким расхождением — иметь НИЗКОЕ расхождение, но не ОТСУТСТВИЕ расхождения, поскольку отсутствие расхождения — это регулярно распределенная выборка, которая имеет некоторые плохие свойства, включая наложение спектров.
Вместо вывода
Если вы на минуту остановитесь и присмотритесь к алгоритму генерации Plus LDG и R2, то заметите схожесть в их строении. Если ещё минуту присмотерться, то можно выписать обе функции как:
z = (x A + y
B) mod 1
, где для Plus
, и
.
В то же время, для R2 ,
К сожалению, формула IGN выбивается, однако я не думаю, что две операции mod необходимы, если изначально подобрать правильные магические числа. К сожалению, я не знаю как можно аналитически вывести эти числа (или доказать, что их нельзя вывести).
Спойлер
Нечто прямолинейное вроде float2(magic.z magic.x, magic.z
magic.y) не работает и приводит к потери свойств IGN.
Как же так вышло, что эту простую формулу обнаружили только недавно? Ответ в том, что её до этого несколько раз независимо друг от друга переизобретали, но распространение она получила только недавно.
Christian Cann Schuldt Jensen, когда разрабатывал SweetFX в 2011, искал быстрейший способ получения дизернга, т.к. его инжектор не позволял семплировать пользовательский текстуры, так что ему приходилось использовать математику. Он обнаружил, что frac(dot(coordinates, MAGIC_NUMBERS) даёт хорошие результаты, причём если смещать зелёный компонент (потому что наши глаза наиболее чувствительны к зелёному) rgb в обратную сторону от rb, то можно создать дешёвую (в плане производительности) иллюзию наличия большего диапазона переходных цветов.
Øyvind Kolås для Gimp в 2013 также независимо написал свой дизеринг, только в этот раз для CPU.
Позднее, Pascal Richer (Marty из MartyMods) также переизобрёл этот алгоритм, только с другими магическими числами.
Где-то в это время похожий алгоритм использовали в Valve для их Half-life 2 HDR lighthouse demo. Также его использовали в ID software/Bethesda для Doom Eternal.
А также, скорее всего, этот алгоритм переоткрывали много раз за закрытыми дверьми.
Я думаю, что причина, по которой его так много открывают заново, заключается в сочетании простоты, и того, что существует так много комбинаций магических чисел, которые хорошо работают, что найти хорошую несложно.
Кроме того, синий шум по-прежнему можно считать лучшим по качеству дизеринга (кроме особых случаев), поэтому, чтобы конкурировать с ним, нужно быть либо быстрее, либо лучше, и поскольку мы, вероятно, не можем сделать лучше (это вопрос поиска лучшего генератора синего шума), то нам нужно быть быстрее, чем семплирование текстуры.
И этот поиск чего-то более быстрого, чем семплирование текстуры, обычно заканчивается на этом алгоритме.
Думаю, этой области необходимо дальнейшее изучение и категоризация "магических чисел", ведь множество из них обладают "магическими свойствами", которые могут оказаться полезными. К сожалению, только игровые разработчики осознали ценность этого алгоритма, поскольку пока он пока полезен только в сферах графики в реальном времени.
