Полтора года назад адепты функционального программирования основали сообщество RuHaskell и с тех пор периодически собираются, и проводят митапы. Ну как периодически — уже два раза собирались. Мы тут, в «Лаборатории Касперского», вообще очень поддерживаем это начинание. Во-первых, потому что это интересно, во-вторых, потому что мы используем Haskell в процессе разработки наших решений, а в-третьих, потому что некоторые участники сообщества у нас работают. А потому мы решили собрать третий митап этого сообщества на нашей территории. 18 августа все заинтересованные могут прийти в наш московский офис (Ленинградское шоссе, д.39А, стр.2), послушать умных людей, обсудить Haskell, поделиться опытом, позадавать вопросы и пообщаться. Разумеется, предварительно следует зарегистрироваться вот на этой страничке.

Теоретические основы императивного программирования были заложены ещё в 30-х годах XX века Аланом Тьюрингом и Джоном фон Нейманом. Теория, положенная в основу функционального подхода, формировалась в 20-х и 30-х годах. В числе разработчиков математических основ функционального программирования — Мозес Шёнфинкель (Германия и Россия) и Хаскелл Карри (Англия), а также Алонзо Чёрч (США). Шёнфинкель и Карри заложили основы комбинаторной логики, а Чёрч является создателем лямбда-исчисления.

Функциональное программирование как раз основано на идеях из комбинаторной логики и лямбда-исчисления.

Но теория так и оставалась теорией, пока в начале 50-х прошлого века Джон МакКарти не разработал язык Lisp (1958), который стал первым почти функциональным языком программирования. На протяжении многих лет у Lisp не было конкурентов. Позднее появились функциональные языки программирования APL (1964), ISWIM (1966) и FP (1977), которые не получили столь широкого распространения.

Со временем Lisp перестал удовлетворять некоторым требованиям разработчиков программ, особенно с ростом объема и сложности программного кода.

19 серия культового соревнования начнётся в пятницу, 5 августа, в 0:00 UTC.

ICFP Programming Contest — международное соревнование по программированию, проводимое ежегодно летом с 1998 года. Результаты соревнования объявляются на Международной конференции по функциональному программированию. (с) Wikipedia

Это седьмая статья из цикла «Теория категорий для программистов». Предыдущие статьи уже публиковались на Хабре:

• Теория категорий для программистов: предисловие
• Категория: суть композиции
• Типы и функции
• Категории, большие и малые
• Категории Клейсли
• Произведения и копроизведения
• Простые алгебраические типы данных

Функторы

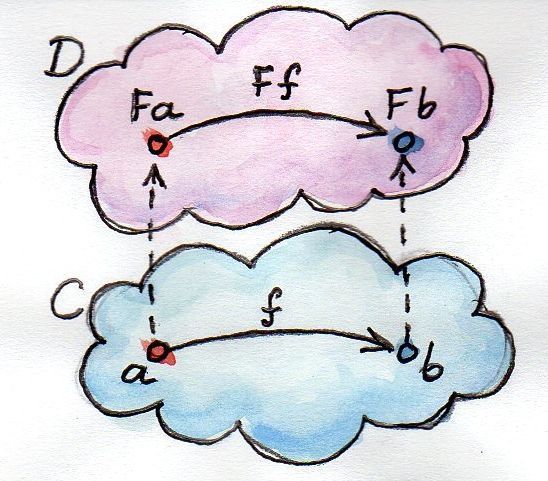
За понятием функтора стоит очень простая, но мощная идея (как бы заезжено это ни прозвучало). Просто теория категорий полна простых и мощных идей. Функтор есть отображение между категориями. Пусть даны две категории C и D, а функтор F отображает объекты из C в объекты из D — это функция над объектами. Если a — это объект из C, то будем обозначать его образ из D как F a (без скобок). Но ведь категория — это не только объекты, но еще и соединяющие их морфизмы. Функтор также отображает и морфизмы — это функция над морфизмами. Но морфизмы отображаются не как попало, а так, чтобы сохранять связи. А именно, если морфизм f из C связывает объект a с объектом b,

f :: a -> b

то образ f в D, F f, связывает образ a с образом b:

F f :: F a -> F b

(Надеемся, что такая смесь математических обозначений и синтаксиса Haskell понятна читателю. Мы не будем писать скобки, применяя функторы к объектам или морфизмам.)

От автора: перевод статьи «Функциональное программирование непопулярно, потому что оно странное» вызвал бурное обсуждение. В нескольких комментариях весьма справедливо замечалось, что при обсуждении недостатков функционального программирования хорошо бы опираться на современные и развитые функциональные языки (в оригинальной статье примеры были на шаблонах C++) и что Хаскель, например, последние пять лет широко используется в индустрии. В связи с этим я хотел бы обратить внимание на две очень предметные статьи из другого блога (от автора книги F# for Scientists): (i) "Недостатки чистого функционального программирования" и (ii) "Почему Хаскель так мало используется в индустрии". Перевод первой из них я как раз и хотел бы представить ниже.

1. На чистых функциональных языках не существует эффективного неупорядоченного словаря и множества

Я подразумеваю, что читатель знает Haskell, по крайней мере, до монад.

Monad – это класс типов, позволяющий (неформально говоря) из функций, которые возвращают что то вроде MyMonad КакойтоТип выполнять некие функции, взаимодействующие с монадой. Функции, использующие монады, нужно связывать между собой специальными функциями (>>),(>>=),(=<<).
Так вот, Comonad – это тоже класс типов, который позволяет функциям взаимодействовать с эффектами комонады, только у этих функций комонада указывается не в возвращаемом типе, а в аргументе.

Это шестая статья из цикла «Теория категорий для программистов». Предыдущие статьи уже публиковались на Хабре:
0. Теория категорий для программистов: предисловие
1. Категория: суть композиции
2. Типы и функции
3. Категории, большие и малые
4. Категории Клейсли
5. Произведения и копроизведения

В предыдущей статье были рассмотрены базовые операции над типами: произведение и копроизведение. Теперь покажем, что комбинирование этих механизмов позволяет построить многие из повседневных структур данных. Такое построение имеет существенное прикладное значение. Например, если мы умеем проверять на равенство базовые типы данных, а также знаем, как свести равенство произведения и копроизведения к равенстве компонент, то операторы равенства для составных типов можно вывести автоматически. В Haskell для обширного подмножества составных типов автоматически выводятся операторы равенства и сравнения, конвертация в строку и обратно и многие другие операции.

Рассмотрим подробнее место произведения и копроизведения типов в программировании.

Произведение типов

Каноническая реализация произведения типов в языках программирования — это пара. В Haskell пара является примитивным конструктором типов, а в C++ это относительно сложный шаблон из стандартной библиотеки.

Строго говоря, произведение типов не коммутативно: нельзя подставить пару типа (Int, Bool) вместо (Bool, Int), хотя они и содержат одни и те же данные. Однако произведение коммутативно с точностью до изоморфизма, задаваемого функцией swap, которая обратна самой себе:

swap :: (a, b) -> (b, a)
swap (x, y) = (y, x)

Можно рассматривать такие пары как различные форматы хранения одной и той же информации, как big endian и little endian.

Данный пост является попыткой добавить пару капель топлива в машину пропаганды Haskell, демонстрируя его использование в повседневных задачах.



В качестве таковых рассмотрим следующие:

• Реализуем пакет доступа к API ВКонтакте.
  Код будет работать как в «native» приложениях, так и в приложениях JavaScript через GHCJS, компилятор Haskell в JavaScript
  
• Напишем одностраничное браузерное приложение, используя наше API
  

— Для чего нужны монады?
— Для того, чтобы отделить чистые вычисления от побочных эффектов.
(из сетевых дискуссий о языке Haskell)

Шерлок Холмс и доктор Ватсон летят на воздушном шаре. Попадают в густой туман и теряют ориентацию. Тут небольшой просвет — и они видят на земле человека.
— Уважаемый, не подскажете ли, где мы находимся?
— В корзине воздушного шара, сэр.
Тут их относит дальше и они опять ничего не видят.
— Это был математик, – говорит Холмс.
— Но почему?
— Его ответ совершенно точен, но при этом абсолютно бесполезен.
(анекдот)

Когда древние египтяне хотели написать, что они насчитали 5 рыб, они рисовали 5 фигурок рыб. Когда они хотели написать, что насчитали 70 людей, они рисовали 70 фигурок людей. Когда они хотели написать, что насчитали в стаде 300 овец, они… — ну, в общем, вы поняли. Так и мучились древние египтяне, пока самый умный и ленивый из них не увидел нечто общее во всех этих записях, и не отделил понятие количества того, что мы подсчитываем, от свойств того, что мы подсчитываем. А потом другой умный ленивый египтянин заменил множество палочек, которыми люди обозначали количество, на значительно меньшее количество знаков, короткой комбинацией которых можно было заменить огромное количество палочек.

То, что сделали эти умные ленивые египтяне, называется абстракцией. Они подметили нечто общее, что свойственно всем записям о количестве чего-либо, и отделили это общее от частных свойств подсчитываемых предметов. Если вы понимаете смысл этой абстракции, которую мы сегодня называем числами, и то, насколько она облегчила жизнь людям, то вам не составит труда понять и абстракции языка Haskell — все эти непонятные, на первый взгляд, функторы, моноиды, аппликативные функторы и монады. Несмотря на их пугающие названия, пришедшие к нам из математической теории категорий, понять их не сложнее, чем абстракцию под названием «числа». Для их понимания совершенно не требуется знать ни теорию категорий, ни даже математику в объёме средней школы (арифметики вполне достаточно). И объяснить их тоже можно, не прибегая к пугающим многих математическим понятиям. А смысл абстракций языка Haskell точно такой же, как и у чисел — они значительно облегчают программистам жизнь (и вы пока даже не представляете, насколько!).

Это пятая статья из цикла «Теория категорий для программистов». Предыдущие статьи уже публиковались на Хабре в переводе Monnoroch:
0. Теория категорий для программистов: предисловие
1. Категория: суть композиции
2. Типы и функции
3. Категории, большие и малые
4. Категории Клейсли

На КДПВ поросенок Петр заводит по одному трактору в каждый объект категории.

Следуй по стрелкам

Древнегреческий драматург Еврипид писал «Всякий человек подобен своему окружению». Это верно и для теории категорий. Выделить определенный объект категории можно только путем описания характера его взаимоотношений с другими объектами (и самим собой), где отношения — это морфизмы.

Для определения объектов в терминах их взаимоотношений теория категорий прибегает к т. н. универсальным конструкциям. Для этого можно выбрать некоторый шаблон, диаграмму из объектов и морфизмов определенной формы, и рассмотреть все подходящие под него конструкции рассматриваемой категории. Если шаблон достаточно распространен и категория достаточно велика, то, вероятно, найденных конструкций будет очень и очень много. Идея универсальной конструкции состоит в том, чтобы упорядочить конструкции по какому-то закону и выбрать наиболее подходящую.

Этот процесс можно сравнить с поиском в сети. Запрос пользователя — это наш шаблон. Если запрос не очень специфичен, то в ответ поисковая система выдаст множество подходящих документов, только часть из которых релевантны. Чтобы исключить нерелевантные ответы, пользователь уточняет запрос, что увеличивает точность поиска. В конце концов поисковая система проранжирует совпадения и, если повезет, искомый результат будет в самом начале списка.

В данной статье приведено краткое описание техники, которое позволяет использовать в программах на Haskell библиотеки, написанные на других языках программирования. При этом нет необходимости ни переписывать эти библиотеки на Haskell, ни писать бесчисленные обертки на C, ни писать явные байндинги. В получающейся программе можно как напрямую вызывать “чужой” код, так и вызывать из чужого кода Haskell функции. Сам же код функций может быть написан на расширенном подключаемом языке, что позволяет работать с ним специалистам в подключаемых языках, которые, к сожалению, пока не знакомы с Haskell.

Перевод статьи о вопросе выбора языка и компромиссе сложности и продуктивности.

Предупреждение: это разглагольствование.

Недавно я сделал очередной большой шаг вперед на своём пути просвещения в Хаскеле. Наконец-то я вижу, как много различных частей мозаики Хаскеля гармонично складываются воедино. На этом моменте, я почувствовал, что готов идти вперёд и писать полезные программы. Я прочёл исходный код web-фреймворка Scotty и был приятно удивлён тем, что я прекрасно понимал, как он работает. Я полностью влюблён в Хаскель. Мне нравится, что он заставляет тебя думать. Ты не просто открываешь текстовый редактор и начинаешь ударять по клавишам, чтобы написать программу на Хаскеле. Я люблю то, что Хаскель поощряет обобщения и абстракции. Одним из «эврика»-моментов в моём пути было понимание всех последствий того, почему функция типа a -> a имеет только одну реализацию. Я подсел на возможность запустить программу в первый раз и знать, что она заработает (после борьбы с компилятором целую вечность). Я думаю, что монады и линзы — очень умные вещи. Да по многим критериям, Haskell — идеальный язык программирования.

И у меня заняло 4 года прийти к этому.

Одри Тан в первую очередь известна как создатель и разработчик Pugs, Perl 6 User’s Golfing System, реализации Perl 6 на Haskell, которая появилась 1 февраля 2005 года и была наиболее активно разрабатываемой и наиболее полной реализацией на то время.

Предлагаю читателям «Хабрахабра» вольный перевод статьи «Functional programming in Kotlin». Автор публикации — Mike Hearn.



Те, кто используют .NET, наверняка слышали про F#, универсальный функциональный язык программирования для CLR. Программисты же вне .NET сообщества скорее всего знают про функциональное программирование в связи с языком Haskell.

Так или иначе, я подозреваю что многим пришелся бы по душе схожий язык, но для JVM, с развитыми инструментами и без необходимости делать все подряд в функциональном стиле.

Язык Kotlin (kotlinlang.org) от JetBrains может показаться всего лишь подслащенной Java: синтаксические конвенции, автовывод типов (type inference) и тому подобные мелочи. Но под незамысловатой оболочкой в нем можно найти все самые популярные и прогрессивные конструкции функциональных языков.

От переводчика:
Это вольный перевод статьи «Purify code using free monads» Габриэля Гонзалеса, посвященный использованию свободных монад для представления кода как синтаксического дерева с последующей управляемой интерпретацией.
На хабре имеются другие статьи Габриэля — «Кооперативные потоки с нуля в 33 строках на Хаскеле» и «Чем хороши свободные монады».
Для прочтения этой статьи необходимо знать, что такое свободная монада и почему она является функтором и монадой. Узнать об этом можно в указанных двух переводах или в статье, на которую ссылается сам автор.
Все замечания переводчика выделены курсивом.
По всем замечаниям, связанным с переводом, обращайтесь в личку.

Опытные программисты на Хаскеле часто советуют новичкам делать программы настолько чистыми, насколько это возможно. Функция называется чистой, если она детерминированная (возвращаемое значение однозначно определяется значениями всех формальных аргументов) и не имеет побочных эффектов (то есть не изменяет состояние среды исполнения). В классической математике, λ-исчислении и комбинаторной логике все функции чистые. Чистота предоставляет множество практических преимуществ:

• можно формально доказать какие-то свойства написанного кода,
• кроме того, можно легко обозревать код и сказать, что он делает,
• наконец, можно прогнать через QuickCheck.

Для демонстрации я буду использовать такую простенькую программу echo:

import System.Exit

main = do x <- getLine
          putStrLn x
          exitSuccess
          putStrLn "Finished"

В приведённой программе, однако, имеется один недостаток: в ней смешаны бизнес-логика и побочные эффекты. В конкретном случае в этом нет ничего плохого, я всегда так пишу простенькие программы, которые могу целиком держать в голове. Впрочем, я надеюсь вас заинтересовать прикольными штуками, которые получаются, когда побочные эффекты отделены от бизнес-логики.

Привет!

15 августа состоится FPConf — первая в России конференция по функциональному программированию. В двух потоках однодневной конференции будут доклады о Scala, F#, Erlang, Clojure, Haskell и функциональных подходах в привычных Ruby, Python и Java.

Мы искренне считаем, что функциональные подходы сегодня — новый мэйнстрим, точка развития отрасли и полезный инструментарий, который нужен высококлассному разработчику для решения сложных и интересных задач. Прошло время, когда можно ограничиться одним технологическим стеком и быть востребованным. Большие данные, возрастающие нагрузки, профессиональное любопытство и желание развиваться приводят все больше людей к изучению монад, лямбд, замыканий и иммутабельности.

Поэтому, мы приглашаем как опытных функциональщиков, так и тех, кто только хочет получить вдохновение и обзор тем для первого изучения :)

Доклады от представителей JetBrains, Лаборатории Касперского, 2ГИС, Mail.ru, Mashine Zone, Luxoft, Sputnik и многих других.
Цена билета сейчас — 7000 рублей. Регистрация тут.


Программа:

Эдвард Кметт, Chair of the Haskell Core Libraries Committee
LENSES AND PRISMS
Functional programming shows us that working with immutable structures makes it easy to reason about parallelism, non-determinism, and other effects, but along the way we lose the familiar notion of a field accessor. «Getters and setters» don't make sense as such in an immutable world. Lenses provide us a way to regain that lost functionality and more besides, acting as a form of «functional reference».
On the flip side, in the process of constructing the lenslibraryfor Haskell, I've found a related notion, that of a Prism, to be equally useful for working with case matching on ADTs, handling extensible exceptions, as well as working with semi-structured data such as JSON, XML and the like. However, surprisingly little has been said about them before now.
This talk will explore the roles each of these abstractions play and why you as a developer should care about them.

Рассмотрим типичную задачу, из тех, что обычно считаются «ООП-эшными». Имеется список данных (объектов) имеющих не одинаковые структуры (по научному, гетерогенный список), при чём, над каждым нужно выполнять одинаковые действия – по простому, каждый можно передать в некую функцию.

Некоторое время назад я решил поэкспериментировать с микросервисами на Haskell. Архитектура проекта подразумевает создание большого количества микро-проектов, каждый из которых отвечает за один небольшой объем задач. Через какое-то время мне надоело создавать эти проекты вручную, а также писать шаблонный код для каждой сущности из БД. Для решения этой проблемы я разработал небольшую утилиту, позволяющую генерировать шаблонный код. Под катом — подробнее.

Очень удивительно (я бы даже сказал — внезапно!), но кортеж-пара в GHC является функтором. Это сложно понять, ведь функтор должен иметь только один параметр, а у пары их два. Можно восхищаться тем, как разработчики стандартной библиотеки GHC умудрились предоставить такую абстракцию, но мне кажется, полученное решение все же следует признать неудачным.

Начнем с того, что оно интуитивно непонятно. Скажем, попробуйте вычислить вручную, не используя инструментов GHC, выражение (1+) `fmap` (2, 3). А после этого проверьте полученный результат, например, в ghci. У многих ли результат ручного вычисления совпал с тем, который выдала система? И если у вас результаты все же совпали, мне очень хотелось бы услышать хорошее объяснение того, как именно вам это удалось.

Некоторое время назад я окончательно устал от языков с динамической типизацией и решил попробовать изучить что-нибудь брутально-статическое. Haskell приглянулся мне красотой кода и бескомпромиссным стремлением явно отделить чистые функции от производящих сайд-эффекты. Я залпом проглотил несколько книжек по Haskell и решил, что пора что-нибудь уже и написать.

И тут-то меня ждало разочарование: я не был способен написать ничего кроме hello world-a. Т.е. я примерно представлял себе, как написать какую-нибудь консольную утилиту типа find или вроде того, — но первая же встреча с IO разрушала все мои представления. Библиотек для Haskell вроде бы много, а документации по ним почти совсем нету. Примеров решения типовых задач тоже очень мало.

Симптомы понятны, диагноз простой: отсутствие практики. А для Haskell это достаточно болезненно, т.к. язык крайне необычный. Даже то, что я неплохо знаю Clojure, почти никак мне не помогло, т.к. Clojure больше фокусируется на функциях, в то время как Haskell — на их типах.

Думаю, многие новички столкнулись с проблемой отсутствия практики в Haskell. Писать что-то совсем уж без интерфейса как-то не интересно, а сделать desktop- или web-приложение для начинающего хаскелиста довольно сложно. И в этой статье я собираюсь предложить простой пример, как написать сервер веб-приложения на Haskell специально для тех, кто хочет попрактиковаться в Haskell, но не знает, с какой стороны к нему подойти.

Для самых нетерпеливых: исходники здесь.