
По правилам сокращений в заголовке не должно быть, но расписав сокращения я превратил бы заголовок в аннотацию. Так что вот…
- БИНС — бесплатформенная инерциальная навигационная система
- БПЛА — беспилотный летательный аппарат
- ОЧ — ось чувствительности датчика
Речь в статье пойдет о навигационной системе, в которой ОЧ датчиков ориентированы неортогонально, т.е. расположены под некоторым, ненулевым, углом к осям системы координат, связанной с БПЛА. Особенность таких БИНС в том, что по информации от каждого из датчиков можно получить значения всех трех компонент угловой скорости (для гироскопов) и линейного ускорения (для линейных акселерометров) объекта.
Статья написана как дополнение к Строим мультикоптер, часть вторая. Целью является описание одного из способов борьбы с дрейфом нуля в дешевых датчиках.
ВВЕДЕНИЕ
Преимуществами БИНС являются относительная дешевизна (имеется возможность применения датчиков из категории «low cost»), малые габариты и вес, а также малое энергопотребление. Эти преимущества особенно хорошо видны в БИНС, построенных на микромеханических навигационных датчиках (гироскопах – ММГ, акселерометров – ММА).
Блоки линейных микромеханических акселерометров используются как датчики кажущегося ускорения подвижного объекта в составе инерцииальных навигационных систем. Они не обладают высокими точностными характеристиками (если рассматривать недорогие ММА). Однако имеются задачи, для решения которых они хорошо подходят. Например, в малоразмерных летательных аппаратах малые габариты и вес вкупе с низким энергопотреблением блоков ММА приносят много выгоды. То же самое касается и автомобилестроения, где они комплексируются со спутниковыми системами (GPS, ГЛОНАСС или др.).
Одной из серьезных проблем недорогих микромеханических датчиков является случайный дрейф нуля. Попросту говоря, дрейф — это когда датчик показывает, что объект вращается (дрейф ММГ), хотя на самом деле вращения нет. У дрейфа есть постоянная составляющая, которую можно скомпенсировать, и случайная, которую скомпенсировать трудно. Существуют разные способы борьбы со случайной погрешностью. Одним из них является построение неортогональной БИНС с информационной избыточностью.
В данной статье повествование пойдет на примере блока четырех двухосных ММА ADXL-203CE, ОЧ которых ориентированы параллельно образующим двух конусов. Оптимальная величина угла полураствора конуса для одноосных измерителей составляет 54,75 градуса [1]. Для двухосных датчиков приходится применить схему расположения ОЧ на двух конусах. Такая конструкция описана в патенте РФ №1810299, “Блок инерциальных чувствительных элементов с избыточной структурой”.
ИЗБЫТОЧНЫЙ БЛОК
Для создания информационной избыточности нужно, чтобы число измерительных каналов (осей чувствительности) в блоке было больше числа измеряемых параметров. Для блока 4-х двухосных датчиков мы получаем 8 измерительных каналов, чего вполне достаточно для построения нормальной БИНС. При этом, как говорилось выше, ОЧ датчиков должны быть ориентированы параллельно образующим конуса. Для создания такой конструкции необязательно делать конус и даже пирамиду. Датчики можно разместить на боковую поверхность параллелепипеда и повернуть их вокруг нормали к боковой грани. Получится следующее
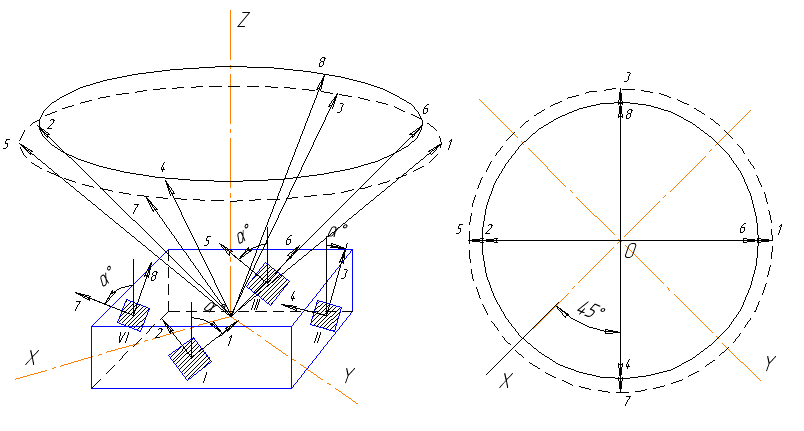
Рис. 1. Конструкция избыточного блока.
Сами датчики могут продаваться будучи уже распаяными на миниплаты с монтажными отверстиями. Основу для блока можно сделать из текстолита (из пластика, дерева и пр.). Точность монтажных отверстий в основании играет второстепенную роль. У самих датчиков внутренняя погрешность ориентации достаточно велика. После сборки такой БИНС в любом случае нужно провести калибровку датчиков для определения фактических значений матрицы направляющих косинусов и масштабных коэффициентов [2].
Для такой ориентации датчиков требуется составить матрицу направляющих косинусов. Эта матрица состоит из косинусов углов между ОЧ датчика (строки) и осями объектового координатного трехгранника (столбцы). Для построения матрицы направляющих косинусов можно использовать метод последовательных поворотов [3, 4].
При указанном выше монтаже датчиков получим следующую схему поворотов.

Рис. 2. Схема поворотов датчика в блоке
При этом в итоге получится матрица [8x3] — восемь осей чувствительности датчиков и три оси связанной системы координат. Для проверки правильности составления матрицы направляющих косинусов имеется несколько критериев:
- векторы-строки матрицы Н имеют норму, равную 1
- Любые три строки линейно-независимы (требование отсутствия в блоке двух параллельных и трех компланарных ОЧ)
- матрица (HT*H)-1 — ковариационная матрица ошибок, является диагональной с элементами в диагонали, меньшими единицы.
Для оплимальной ориентации ОЧ (на поверхности одного конуса с углом полураствора 54.75 градуса) имеем:

Это означает, что при данной ориентации ОЧ дисперсия ошибок по осям ОХ и ОY уменьшится в корень из 2, а по ОZ в два раза [1].
ОБРАБОТКА ИНФОРМАЦИИ ИЗБЫТОЧНОГО БЛОКА
В простейшем случае для получения оценки компонент вектора абсолютной угловой скорости (или кажущегося ускорения) потребуется решить систему линейных алгебраических уравнений (СЛАУ), в правых частях которых выходные сигналы датчиков, независимые переменные — искомые компоненты вектора угловой скорости (ускорения), а коэффициенты — элементы матрицы направляющих косинусов. Вследствие информационной избыточности полученная СЛАУ будет переопределенной (число уравнений больше числа переменных). В общем случае такая система решений (точных) не имеет. Для ее приближенного решения можно воспользоваться, например, простым алгоритмом гауссовского метода наименьших квадратов:

С помощью этого выражения вычисляется псевдообратная к прямоугольной матрица. Данный метод накладывает серьезные ограничения на подавляемые шумы (нулевое среднее, гауссов шум, равные дисперсии шумов в разных измерительных каналах).
Чуть более сложным является алгоритм гауссовско-марковского МНК (метод взвешенных наименьших квадратов, МВНК):

где N — матрица направляющих косинусов,
С — матрица ковариаций измерительных шумов.
Из МВНК выводится рекуррентный гауссовско-марковский МНК, который в [5] называется фильтром Калмана-Бьюси:


В этом алгоритме не учитывается динамическая модель датчиков.
Следующий алгоритм — фильтр Калмана, учитывающий динамику датчиков:


В пособии [5] эти алгоритмы описаны подробно, там же вы найдете обобщение фильтра Калмана на различные частные случаи шумов, схемы совокупной системы «блок — наблюдающее устройство».
Помимо алгоритмов на основе МНК можно воспользоваться, к примеру, нейросетями для решения систем уравнений [6]
КАЛИБРОВКА БЛОКА
Если используются датчики с аналоговым выходом, то нужно откалибровать масштабные коэффициенты датчиков, чтобы приводить вольты к угловой скорости и ускорению. Для датчиков с цифровым выходом (например, у Analog Devices есть микромеханика с SPI-интерфейсом) масштабный коэффициент калибровать не нужно. Также нужно откалибровать матрицу направляющих косинусов, т.е. определить реальные значения углов ориентации уже смонтированного блока (основание «на коленке» не изготовить точно, плюс погрешности распайки датчиков на несущие платы и внутренние неидеальности). Можно подумать, что если датчики сильно шумят, то и с калибровкой нет смысла заморачиваться. Однако калибровкой мы устраняем смещение среднего шумов. Поэтому калибровка все-таки важна.
Как калибровать? Для блока акселерометров это можно делать в поле тяготения Земли. Для гироскопов тоже, если вы знаете вертикальную составляющую вращения планеты в своем местоположении.
При работе над дипломом я пользовался лабораторной установкой, состоящей из избыточного блока, АЦП, ПК и поворотного стола.

Главная трудность тут — поворотный стол. Думаю, это приспособление в «Юном Технике» не продается. Также желательно «мини лабораторию» организовать на «развязанном» фундаменте, где-то вдали от автострады. Как указано в Строим мультикоптер, часть вторая, ММА достаточно чувствительны. Если «пошуршать» по столу, на котором размещен блок, то вы увидите это невооруженным глазом на графиках выходных сигналов.
Методика калибровки масштабного коэффициента может быть следующей.
- Сделать в грани основания несколько групп отверстий для закрепления платы с датчиком под разными углами (дискретность, к примеру, 15 градусов).
- Выставить основание к горизонту так, чтобы датчик выдавал максимальное положительное значение (если у датчика применено смещение нуля сигнала, то просто максимальное)
- Поворачивая датчик по 15 градусов вокруг нормали к грани мы получим несколько значений от максимума до минимума (от +1g до -1g)
По полученным замерам легко можно построить линию тренда, наклон которой и будет масштабным коэффициентом. Но нужно учесть, что вблизи нуля показания датчика сильнее отклоняются от тренда.
Для толковой калибровки матрицы направляющих косинусов желательно наличие поворотного стола. Если такового нет, то нужно как можно точнее выставлять грань блока ММА с калибруемым датчиком перпендикулярно всем трем плоскостям местного координатного трехгранника и по показаниям датчика определять его углы в грани основания. Если вы уверены в том, что ваше основание параллелепипед, то задача несколько упрощается.
ЗАКЛЮЧЕНИЕ
Каков эффект от неортогональности и избыточности? Т.к. мы боремся со случайным дрейфом, который может быть как положительным, так и отрицательным, то при суммировании проекций дрейфов на объектовые оси координат мы получим уменьшение общего дрейфа измерений (конечно, при оптимальной ориентации). Усилить эффект можно ориентированием одной ОЧ по оси конуса (подходит для нечетного числа измерительных каналов).
Еще один немаловажный эффект — повышение надежности за счет избыточного числа датчиков. Выход из строя измерительного канала будет приводить лишь к увеличению погрешности измерений (пока в блоке работают 4 и более измерительных канала). Таким образом, можно построить алгоритм, который будет адаптироваться к возможным неисправностям. В случае отказов даже не нужно будет модифицировать алгоритмы (перестраивать матрицу направляющих косинусов), достаточно будет поставить для отказавшего канала слишком большое значение дисперсии в ковариационных матрицах МВНК и ФК.
СПИСОК ЛИТЕРАТУРЫ
1. Водичева Л. В. Повышение надежности и точности бесплатформенного инерциального измерительного блока при избыточном количестве измерений // Гироскопия и навигация. 1997. № 1. — С. 55-67.
2. Алешкин М.В. Математические модели, методы и алгоритмы обработки избыточной информации измерительного блока / В.В. Алешкин, A.C. Матвеев, М.В. Алешкин // Интернет и инновации: сб.трудов Междунар. конф. Саратов: СГТУ, 2008. С. 377-380.
3. Схема поворотов
4. Поворот в н-мерном пространстве
5. Браммер К., Зиффлинг Г. Фильтр Калмана-Бьюси. Детерминированное наблюдение и стохастическая фильтрация
6. Нейронные сети. Решение систем нелинейных уравнений
