
Искать счастье бесполезно, главное — где оно найдет тебя. Некоторые, в том числе и я, заимел привычку проверять маршрутные проездные билеты на предмет этого «счастья» — билет можно назвать «счастливым», если сумма его первых трех цифр равняется сумме трех остальных. Забавное такое, знаете ли, занятие.
Но иногда бывает так, что счастливые билеты попадаются очень часто, а иногда — их не бывает и несколько месяцев. Это если ездить один раз в день по какому-нибудь маршруту.
И тут приходит замечательный вопрос: «сколько всего существует счастливых билетов?», а еще лучше, когда приходит математика с ее не менее красивым вопросом: «какова вероятность покупки счастливого билета?»
Для человека, который постиг азы программирования, не составит большого труда написать программу для подсчета этого самого количества счастливых билетов — обычным методом перебора. Что сделал и я, получив результат — 55 251 билет, который говорит, что примерно каждый восемнадцатый билет будет счастливым.
Но теперь представьте себе образ кондуктора — человека-сумка-через шею, с несколькими килограммами мелочи и катушкой билетов, которые он выдает последовательно за определенную плату. И что будет, если вы станете счастливым обладателем билета с номером «010100»? Правильно, счастливобилетчиков на этом маршруте не будет, пока кондуктор не покончит с этой катушкой.
Теперь попробуем ответить на этот вопрос математически.
Максимально возможно счастливый билет «999999» имеет сумму триад равную 27 = 9+9+9 = 9+9+9. Билетов с суммой счастливых цифр равной 1 будет 9, это билеты:
001001 010001 100001
001010 010010 100010
001100 010100 100100
Билетов с суммой счастливых цифр равной 3 будет 36. Можете посчитать сами — любым методом. Составим таблицу для каждой такой комбинации:
Сумма триад / Количество счастливых билетов в группе
1 / 9
2 / 36
3 / 100
4 / 225
5 / 441
6 / 784
7 / 1296
8 / 2025
9 / 3025
10 / 3969
11 / 4761
12 / 5329
13 / 5625
14 / 5625
15 / 5329
16 / 4761
17 / 3969
18 / 3025
19 / 2025
20 / 1296
21 / 784
22 / 441
23 / 225
24 / 100
25 / 36
26 / 9
27 / 1
Сумма: 55251
Получается, что максимальное количество счастливых билетов будет в группах, сумма триад которых равняется 13 или 14.

В таких катушках каждый девятый билет будет счастливым, пока сумма двух цифр одной триады не превзойдет значения 13…14. Следовательно, можно логически предположить, что каждый 18 билет в такой группе будет счастливым. А ввиду такого «классического» распределения, то и во всей группе билетов от 000001 до 999999.
Осталось вспомнить один из методов теории вероятностей, и посчитать:
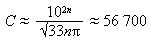
Получая результат с хорошей точностью, с отклонением ≈ 3%.
А еще, счастливые билеты нужно съедать, чтобы ощутить этот прилив вселенского счастья.
Будьте счастливы!