Привет, %username%!
Пару недель назад я опубликовал пост Эллиптическая криптография: теория, в котором постарался описать основные аспекты использования эллиптических кривых в криптографии. Тот мой пост носил исключительно ознакомительный характер, и не предусматривал никакой иной работы с компилятором, кроме созерцательной. Но что за теория без практики? С целью исправить это упущение я, собравшись с духом, ринулся в бой с ГОСТ-ом 34.10-2012, схемой ЭЦП на эллиптических кривых. Если вам интересно посмотреть что из всего этого получилось, тогда добро пожаловать под кат.
Выбор эллиптической кривой
Напомню, что в эллиптической криптографии используются т.н. «кривые над конечным полем». Это означает, что кривые имеют конечное число точек. Количество точек подобной кривой называется порядком кривой. Чтобы использовать эллиптическую кривую в криптографии необходимо знать ее порядок. Это обуславливается хотя бы тем, что от порядка кривой зависит криптостойкость системы, о чем я писал в своем предыдущем опусе.
Именно в этом и заключается вся сложность. Процесс выбора кривой можно записать следующим образом:
- Выбор параметров a и b, описывающих уравнение прямой
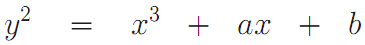
- Подсчет точек выбранной кривой;
- Проверка отвечает ли выбранная кривая с заданным количеством точек ряду условий.
Так вот, проблема состоит в том, что вычисление порядка эллиптической кривой является весьма нетривиальной задачей.
Наиболее распространенный метод вычисления количества точек алгоритм Шуфа имеет достаточно большую вычислительную сложность
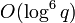. К тому же, алгоритм использует очень серьезные математические методы и весьма сложен для понимания.Есть еще один способ, т.н. метод комплексного умножения. Информацией об этом методе любезно поделился добрый хабрачеловек grechnik в своем посте Представление чисел суммой двух квадратов и эллиптические кривые. Если кратко, то этот метод позволяет гораздо более эффективно находить кривые с заданным количеством точек. Однако в отличие от алгоритма Шуфа, который является универсальным, метод комплексного умножения работает только при выполнении определенных условий. Этот метод тоже не так прост, как может показаться сначала. Более подробно почитать об этом можно например здесь (еще одно спасибо за ссылку, grechnik).
Благо NIST, очевидно в целях
Для описания кривой в стандарте NIST используется набор из 6 параметров D=(p,a,b,G,n,h), где
p — простое число, модуль эллиптической кривой;
a, b — задают уравнение эллиптической кривой
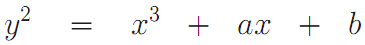;G — точка эллиптической кривой большого порядка. Это означает что если умножать точку на числа меньшие, чем порядок точки, каждый раз будут получаться совершенно различные точки;
n — порядок точки G;
h — параметр, называемый кофактор. Определяется отношением общего числа точек на эллиптической кривой к порядку точки G. Данное число должно быть как можно меньше.
Пара слов о параметрах
Не особо заморачиваясь с выбором, я решил использовать первую рекомендуемую NIST кривую, в которых значение описанных выше параметров соответственно равно:
p=6277101735386680763835789423207666416083908700390324961279;
a=-3;
b=2455155546008943817740293915197451784769108058161191238065;
xG=602046282375688656758213480587526111916698976636884684818 (x-координата точки G);
yG=174050332293622031404857552280219410364023488927386650641 (y-координата точки G);
n=6277101735386680763835789423176059013767194773182842284081;
h=1.
О параметре p, следую рассказать поподробнее. Данное число относится к обобщенным числам Мерсенна, это означает, что его можно представить как сумму различных степеней двойки. Конкретно в нашем случае, число p может быть записано как
p=2192-264-1.
Все эллиптические кривые над полем простого числа, рекомендованные NIST можно записать подобным образом. Использование подобных чисел позволяет ускорить операцию умножения по модулю большого числа. Суть метода сводится к представлению результата умножения в виде машинных слов длиной 32 бита, комбинирование которых дает в результате искомое произведение по модулю большого числа. Подробнее об этом можно почитать, например здесь (спасибо datacompboy за наводку).
Еще один интересный момент связан с координатами точек. Зачастую, в разного рода спецификациях образующая точка G эллиптической кривой задается в сжатой форме. Например, в нашем случае точку G можно задать следующим образом:
G=0x 03 188da80eb03090f67cbf20eb43a18800f4ff0afd82ff1012
Первый байт хранит в себе данные о четности y-координаты. Он может быть равен 2 (это означает что y-координата четная) или 3 (соответственно нечетная). Остальные байты хранят x-координату.
Располагая этими данными мы можем восстановить y-координату следующим образом.
Мы знаем, что точка G принадлежит эллиптической кривой. Соответственно для нее выполняется равенство:
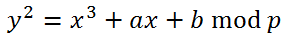
и мы можем вычислить y как:
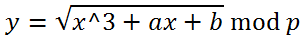.Так как результатом вычисления квадратного корня по модулю p являются два числа y и p-y, мы выбираем то число, четность которого совпадает с четностью первого байта сжатой записи координат G.
Формирование подписи
Прежде чем приступать к реализации самого алгоритма ЭЦП, необходимо написать класс для работы с точками эллиптической кривой. О математических законах и операциях на эллиптических кривых я немного писал в прошлом посте, поэтому не буду сейчас заострять на этом внимание.
Скажу лишь, что для реализации ГОСТ 34.10 нам понадобится всего три операции:
- Сложение двух разных точек;
- Удвоение точки;
- Умножение точки на число.
Немного больше подробностей вы сможете найти, например, на википедии.
Реализацию класса ECPoint, позволяющего выполнять эти действия смотрите под спойлером.
ECPoint.cs
public class ECPoint
{
public BigInteger x;
public BigInteger y;
public BigInteger a;
public BigInteger b;
public BigInteger FieldChar;
public ECPoint(ECPoint p)
{
x = p.x;
y = p.y;
a = p.a;
b = p.b;
FieldChar = p.FieldChar;
}
public ECPoint()
{
x = new BigInteger();
y = new BigInteger();
a = new BigInteger();
b = new BigInteger();
FieldChar = new BigInteger();
}
//сложение двух точек P1 и P2
public static ECPoint operator +(ECPoint p1, ECPoint p2)
{
ECPoint p3 = new ECPoint();
p3.a = p1.a;
p3.b = p1.b;
p3.FieldChar = p1.FieldChar;
BigInteger dy = p2.y - p1.y;
BigInteger dx = p2.x - p1.x;
if (dx < 0)
dx += p1.FieldChar;
if (dy < 0)
dy += p1.FieldChar;
BigInteger m = (dy * dx.modInverse(p1.FieldChar)) % p1.FieldChar;
if (m < 0)
m += p1.FieldChar;
p3.x = (m * m - p1.x - p2.x) % p1.FieldChar;
p3.y = (m * (p1.x - p3.x) - p1.y) % p1.FieldChar;
if (p3.x < 0)
p3.x += p1.FieldChar;
if (p3.y < 0)
p3.y += p1.FieldChar;
return p3;
}
//сложение точки P c собой же
public static ECPoint Double(ECPoint p)
{
ECPoint p2 = new ECPoint();
p2.a = p.a;
p2.b = p.b;
p2.FieldChar = p.FieldChar;
BigInteger dy = 3 * p.x * p.x + p.a;
BigInteger dx = 2 * p.y;
if (dx < 0)
dx += p.FieldChar;
if (dy < 0)
dy += p.FieldChar;
BigInteger m = (dy * dx.modInverse(p.FieldChar)) % p.FieldChar;
p2.x = (m * m - p.x - p.x) % p.FieldChar;
p2.y = (m * (p.x - p2.x) - p.y) % p.FieldChar;
if (p2.x < 0)
p2.x += p.FieldChar;
if (p2.y < 0)
p2.y += p.FieldChar;
return p2;
}
//умножение точки на число x, по сути своей представляет x сложений точки самой с собой
public static ECPoint multiply(BigInteger x, ECPoint p)
{
ECPoint temp = p;
x = x - 1;
while (x != 0)
{
if ((x % 2) != 0)
{
if ((temp.x == p.x) || (temp.y == p.y))
temp = Double(temp);
else
temp = temp + p;
x = x - 1;
}
x = x / 2;
p = Double(p);
}
return temp;
}
}
Для формирования цифровой подписи используется большое число d, которое является постоянным секретным ключом схемы, и должно быть известно только подписывающему лицу.
Для вычисления подписи сообщения M по алгоритму ГОСТ необходимо проделать следующие шаги:
- Вычислить хеш сообщения M: H=h(M). На этом шаге используется хеш-функция Стрибог, о которой я уже писал на хабре;
- Вычислить целое число α, двоичным представление которого является H;
- Определить e=α mod n, если e=0, задать e=1;
- Сгенерировать случайное число k, удовлетворяющее условию 0<k<n;
- Вычислить точку эллиптической кривой C=k*G;
- Определить r = xC mod n, где xC — x-координата точки C. Если r=0, то вернуться к шагу 4;
- Вычислить значение s = (rd+ke) mod n. Если s=0, то вернуться к шагу 4;
- Вернуть значение r||s в качестве цифровой подписи.
Напишем функцию SignGen, реализующую все эти действия:
public string SignGen(byte[] h, BigInteger d)
{
BigInteger alpha = new BigInteger(h);
BigInteger e = alpha % n;
if (e == 0)
e = 1;
BigInteger k = new BigInteger();
ECPoint C=new ECPoint();
BigInteger r=new BigInteger();
BigInteger s = new BigInteger();
do
{
do
{
k.genRandomBits(n.bitCount(), new Random());
} while ((k < 0) || (k > n));
C = ECPoint.multiply(k, G);
r = C.x % n;
s = ((r * d) + (k * e)) % n;
} while ((r == 0)||(s==0));
string Rvector = padding(r.ToHexString(),n.bitCount()/4);
string Svector = padding(s.ToHexString(), n.bitCount() / 4);
return Rvector + Svector;
}
В приведенной части кода функция padding дополняет шестнадцатеричные представления чисел r и s до длины модуля p, чтобы при проверке подписи их можно было распарсить.
Проверка подписи
Для проверки подписи используется точка Q, удовлетворяющая равенству Q=d*G. Точка Q является открытым ключом схемы и может быть известна любому проверяющему.
Процесс проверки подписи происходит по следующему алгоритму:
- По полученной подписи восстановить числа r и s. Если не выполнены неравенства 0<r<n и 0<s<n, тогда вернуть «подпись не верна»;
- Вычислить хеш сообщения M: H=h(M);
- Вычислить целое число α, двоичным представление которого является H;
- Определить e=α mod n, если e=0, задать e=1;
- Вычислить v = e-1 mod n;
- Вычислить значения z1 = s*v mod n и z2 = -r*v mod n;
- Вычислить точку эллиптической кривой C = z1*G + z2*Q;
- Определить R = xc mod n, где xc — x-координата точки C;
- Если R=r, то подпись верна. В противном случае подпись не принимается.
Чтобы понять, почему это работает, запишем процесс проверки подписи в виде формул:
Как видите, мы получаем на этапе проверки ту самую точку C=k*G, что и при формировании подписи.
Функция SignVer, выполняющая проверку:
public bool SignVer(byte[] H, string sign, ECPoint Q)
{
string Rvector = sign.Substring(0, n.bitCount() / 4);
string Svector = sign.Substring(n.bitCount() / 4, n.bitCount() / 4);
BigInteger r = new BigInteger(Rvector, 16);
BigInteger s = new BigInteger(Svector, 16);
if ((r < 1) || (r > (n - 1)) || (s < 1) || (s > (n - 1)))
return false;
BigInteger alpha = new BigInteger(H);
BigInteger e = alpha % n;
if (e == 0)
e = 1;
BigInteger v = e.modInverse(n);
BigInteger z1 = (s * v) % n;
BigInteger z2 = n + ((-(r * v)) % n);
this.G = GDecompression();
ECPoint A = ECPoint.multiply(z1, G);
ECPoint B = ECPoint.multiply(z2, Q);
ECPoint C = A + B;
BigInteger R = C.x % n;
if (R == r)
return true;
else
return false;
}
Функция GDecompression() выполняет «распаковку» точек.
Полностью класс DSGost, реализующий подпись и проверку сообщений по алгоритму ГОСТ 34.10-2012 вы можете посмотреть под спойлером.
DSGost.cs
class DSGost
{
private BigInteger p = new BigInteger();
private BigInteger a = new BigInteger();
private BigInteger b = new BigInteger();
private BigInteger n = new BigInteger();
private byte[] xG;
private ECPoint G = new ECPoint();
public DSGost(BigInteger p, BigInteger a, BigInteger b, BigInteger n, byte[] xG)
{
this.a = a;
this.b = b;
this.n = n;
this.p = p;
this.xG = xG;
}
//Генерируем секретный ключ заданной длины
public BigInteger GenPrivateKey(int BitSize)
{
BigInteger d = new BigInteger();
do
{
d.genRandomBits(BitSize, new Random());
} while ((d < 0) || (d > n));
return d;
}
//С помощью секретного ключа d вычисляем точку Q=d*G, это и будет наш публичный ключ
public ECPoint GenPublicKey(BigInteger d)
{
ECPoint G=GDecompression();
ECPoint Q = ECPoint.multiply(d, G);
return Q;
}
//Восстанавливаем координату y из координаты x и бита четности y
private ECPoint GDecompression()
{
byte y = xG[0];
byte[] x=new byte[xG.Length-1];
Array.Copy(xG, 1, x, 0, xG.Length - 1);
BigInteger Xcord = new BigInteger(x);
BigInteger temp = (Xcord * Xcord * Xcord + a * Xcord + b) % p;
BigInteger beta = ModSqrt(temp, p);
BigInteger Ycord = new BigInteger();
if ((beta % 2) == (y % 2))
Ycord = beta;
else
Ycord = p - beta;
ECPoint G = new ECPoint();
G.a = a;
G.b = b;
G.FieldChar = p;
G.x = Xcord;
G.y = Ycord;
this.G = G;
return G;
}
//функция вычисления квадратоного корня по модулю простого числа q
public BigInteger ModSqrt(BigInteger a, BigInteger q)
{
BigInteger b = new BigInteger();
do
{
b.genRandomBits(255, new Random());
} while (Legendre(b, q) == 1);
BigInteger s = 0;
BigInteger t = q - 1;
while ((t & 1) != 1)
{
s++;
t = t >> 1;
}
BigInteger InvA = a.modInverse(q);
BigInteger c = b.modPow(t, q);
BigInteger r = a.modPow(((t + 1) / 2), q);
BigInteger d = new BigInteger();
for (int i = 1; i < s; i++)
{
BigInteger temp = 2;
temp = temp.modPow((s - i - 1), q);
d = (r.modPow(2, q) * InvA).modPow(temp, q);
if (d == (q - 1))
r = (r * c) % q;
c = c.modPow(2, q);
}
return r;
}
//Вычисляем символ Лежандра
public BigInteger Legendre(BigInteger a, BigInteger q)
{
return a.modPow((q - 1) / 2, q);
}
//подписываем сообщение
public string SignGen(byte[] h, BigInteger d)
{
BigInteger alpha = new BigInteger(h);
BigInteger e = alpha % n;
if (e == 0)
e = 1;
BigInteger k = new BigInteger();
ECPoint C=new ECPoint();
BigInteger r=new BigInteger();
BigInteger s = new BigInteger();
do
{
do
{
k.genRandomBits(n.bitCount(), new Random());
} while ((k < 0) || (k > n));
C = ECPoint.multiply(k, G);
r = C.x % n;
s = ((r * d) + (k * e)) % n;
} while ((r == 0)||(s==0));
string Rvector = padding(r.ToHexString(),n.bitCount()/4);
string Svector = padding(s.ToHexString(), n.bitCount() / 4);
return Rvector + Svector;
}
//проверяем подпись
public bool SignVer(byte[] H, string sign, ECPoint Q)
{
string Rvector = sign.Substring(0, n.bitCount() / 4);
string Svector = sign.Substring(n.bitCount() / 4, n.bitCount() / 4);
BigInteger r = new BigInteger(Rvector, 16);
BigInteger s = new BigInteger(Svector, 16);
if ((r < 1) || (r > (n - 1)) || (s < 1) || (s > (n - 1)))
return false;
BigInteger alpha = new BigInteger(H);
BigInteger e = alpha % n;
if (e == 0)
e = 1;
BigInteger v = e.modInverse(n);
BigInteger z1 = (s * v) % n;
BigInteger z2 = n + ((-(r * v)) % n);
this.G = GDecompression();
ECPoint A = ECPoint.multiply(z1, G);
ECPoint B = ECPoint.multiply(z2, Q);
ECPoint C = A + B;
BigInteger R = C.x % n;
if (R == r)
return true;
else
return false;
}
//дополняем подпись нулями слева до длины n, где n - длина модуля в битах
private string padding(string input, int size)
{
if (input.Length < size)
{
do
{
input = "0" + input;
} while (input.Length < size);
}
return input;
}
}
Пример работы с классом:
private void ECTest()
{
BigInteger p = new BigInteger("6277101735386680763835789423207666416083908700390324961279", 10);
BigInteger a = new BigInteger("-3", 10);
BigInteger b = new BigInteger("64210519e59c80e70fa7e9ab72243049feb8deecc146b9b1", 16);
byte[] xG = FromHexStringToByte("03188da80eb03090f67cbf20eb43a18800f4ff0afd82ff1012");
BigInteger n = new BigInteger("ffffffffffffffffffffffff99def836146bc9b1b4d22831", 16);
DSGost DS = new DSGost(p, a, b, n, xG);
BigInteger d=DS.GenPrivateKey(192);
ECPoint Q = DS.GenPublicKey(d);
GOST hash = new GOST(256);
byte[] H = hash.GetHash(Encoding.Default.GetBytes("Message"));
string sign = DS.SignGen(H, d);
bool result = DS.SignVer(H, sign, Q);
}
Заключение
Мы рассмотрели случай, когда криптосистема построена на эллиптической кривой над полем вычетов по модулю большого простого числа. Однако, не следует забывать что понятие эллиптическая криптография включает в себя гораздо больше, чем этот отдельно взятый случай. И при реализации криптосистем на эллиптических кривых над полями других типов необходимо учитывать, что математические операции на этих кривых могут в значительной степени отличаться от приведенных в данном посте.
PS исходники проекта лежат тут.
