
Число Пи, скажу вам братцы,
Легче так запоминать.
Три четырнадцать пятнадцать
Девять два, шесть пять, три пять.
© Дмитрий Эйт
Недавно мне потребовалось число Пи в шестнадцатиричном формате. Примерно 10000 знаков после запятой. Однако все публикации в сети как правило демонстрируют Пи в десятичном виде. Потыкавшись немного я нашёл Пи в двоичном виде, и это меня более чем устроило: простая конвертация решила поставленные задачи. Тут бы и закончить историю, но как говорится, «ложечка-то нашлась, а осадок остался». Ниже вы сможете посмотреть простую имплементацию библиотеки PiHex, генерирующей цифру, или последовательность цифр в любой позиции после запятой у числа Пи (правда, не более, чем 10,000,000).
Итак, существует алгоритм «BBP», который позволяет вычислить в шестнадцатиричном Пи знак в любой позиции после запятой. Сам этот алгоритм из разряда «краниковых», подробней об этом семействе алгоритмов можно почитать в статье: «Краник», или алгоритм для поиска цифр числа Пи. Об имплементации алгоритма «BBP» на языке Си на хабре также была статья: Вычисление N-го знака числа Пи без вычисления предыдущих
О алгоритме
Описание алгоритма лучше всего прочитать в статье «The BBP Algorithm for Pi», опубликованной Дэвидом Бейли 17 сентября 2006 года: www.davidhbailey.com/dhbpapers/bbp-alg.pdf Кстати говоря, написана она вполне понятно, по крайней мере и не математик тоже может кое-что понять. Из статьи видно, что для расчёта используется не сильно сложная формула в виде:
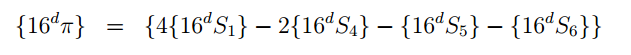
при этом Sj вычисляется как:
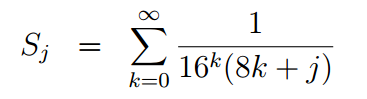
в результате получается немного более громоздкая формула
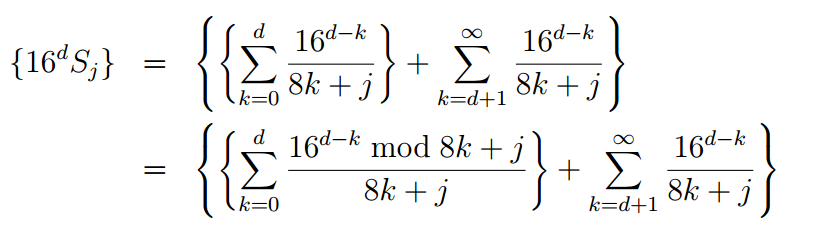
Реализация
При переносе на Go имплементация была реализована с использованием горутин, чтобы распараллелить ресурсоёмкие вычисления Sj. Это позволило значительно ускорить вычисления, так как на современных компьютерах в процессоре обычно ядер больше, чем одно. Впрочем возможно, это не сильно и нужно, если требуется один знак, но если тысяча, скорость работы в любом случае будет важна.
API
Использовать библиотеку не просто, а очень просто, т.к. фактически она поддерживает лишь один метод. Пример ниже показывает, как подключить библиотеку и получить первые 20 знаков после запятой:
package main
import (
"fmt"
"github.com/claygod/PiHex"
)
func main() {
pi := PiHex.New()
fmt.Print("The first 20 digits of Pi (hexadecimal): ", pi.Get(0, 20))
}
Где пригодится библиотека PiHex
Собственно, там, где нужно Пи, и при этом именно в шестнадцатиричном виде. Если требуются большие порядки, то возможно, имеет смысл заранее просчитать Пи и/или пользоваться уже вычисленными результатами, т.к. например на моём компьютере вычисление десяти знаков после 1,000,000 позиции заняло немного более десяти секунд. В связи с ограничением в 10,000,000 знаков после запятой библиотека PiHex никак не подойдёт для установки новых рекордов в вычислении Пи.
Конфигурирование
Реально менять можно только один параметр: STEP. Он указывает, сколько цифр может вычисляться за одну итерацию. По умолчанию стоит 9, и это максимально возможное число, позволяющее сохранить правильность вычисленного результата. Если есть сомнения, цифру можно уменьшать, что правда, уменьшит скорость работы библиотеки.
Тестирование
Поскольку API у библиотеки более чем простое, надеюсь, я смог охватить в тестах все возможные дыры в библиотеке. И да, когда писал тесты, дыры нашлись, без этого не обошлось.
Ссылки
Библиотека PiHex на Гитхабе
Формула Бэйли — Боруэйна — Плаффа
Статья Дэвида Бейли об алгоритме BBP