
Известный всем тест Тьюринга говорит о том, что понять: мыслит машина или нет, можно по тому отличим ли мы ее в беседе от человека или нет. При этом подразумевается, что вестись будет не светская беседа, а, по сути, допрос с пристрастием в котором мы будем всячески пытаться загнать машину в тупик. Что мы при этом будем проверять? Только одно — понимает ли машина суть задаваемых нами вопросов. Пытается ли она, просто, формально манипулировать словами или она может правильно интерпретировать значения слов, используя при этом знания, полученные ранее в беседе, или, вообще, общеизвестные людям знания.
Пожалуй, во время теста не особо интересно спрашивать у машины: когда была Куликовская битва. Гораздо интереснее что она скажет, например, о том: зачем мы нажимаем сильнее на кнопки пульта, у которого садятся батарейки?
Различие человеческого мышления и большинства компьютерных алгоритмов связано с вопросом понимания смысла. Как правило, в компьютерную программу закладываются достаточно жесткие правила, которые определяют то, как программа воспринимает и интерпретирует входную информацию. С одной стороны, это ограничивает вольность общения с программой, но, с другой стороны, позволяет избежать ошибок, связанных с неправильной трактовкой нечетко сформулированных высказываний.
Глобально, проблема передачи смысла, неважно, от человека к человеку или от человека к компьютеру, или между компьютерами, выглядит так: чем четче и однозначнее мы хотим передать сообщение, тем более высокие требования накладываются на согласованность используемых терминов на передающей и принимающей стороне.
Если мы хотим, чтобы программа выполнялась одинаково на любом компьютере, мы создаем условия для однозначной интерпретации всех команд. Когда мы пишем математические формулы, их трактовка не зависит от желания собеседника. Занимаясь наукой, чтобы добиться взаимопонимания, мы используем, где только возможно, не слова обиходного языка, а четко определенные научные термины.
Порою, складывается ощущение, что четкий математико-алгоритмический подход – это более высокий уровень представления информации по сравнению с нечеткой семантикой естественного языка. Но при этом мы часто сталкиваемся с тем, что нам гораздо легче понять сложную мысль не тогда, когда она записана подробно и математически строго, а когда нам кратко и образно на естественном языке объяснят ее суть.
Далее я покажу, что кроется за нечеткими семантическими описаниями и в каком направлении, возможно, стоит двигаться компьютеру, чтобы пройти тест Тьюринга.
Криптография и смысл
Рассмотрим пример из области криптографии. Предположим, что у нас есть поток зашифрованных сообщений. Алгоритм шифрования строится на замене символов исходного сообщения другими символами того же алфавита по правилам, которые определяются шифрующим механизмом и ключом. С чем-то подобным имел дело Алан Тьюринг, взламывая код немецкой «Энигмы».

Предположим, что правила замены букв полностью определяются ключами. Допустим, что есть конечный набор ключей и для каждого ключа заданы правила замены, такие, что каждая буква имеет однозначное соответствие. Тогда, чтобы расшифровать какое-либо сообщение, необходимо перебрать все ключи, применить обратную перекодировку и попробовать понять, не встретится ли среди вариантов расшифровки какой-либо осмысленный.
Для определения осмысленности потребуется словарь со словами, которые могут встретится в раскодированном сообщении. Как только сообщение примет вид, в котором слова сообщения совпадут со словами из словаря, можно будет сказать, что мы нашли правильный ключ и получили расшифрованное сообщение.
Если мы захотим ускорить подбор ключа, то нам придется распараллелить процесс проверки. В идеале можно взять столько параллельных процессоров сколько может быть различных ключей. Распределить ключи по процессорам и выполнить на каждом процессоре раскодирование со своим ключом. Затем на каждом процессоре сделать проверку полученного результата на осмысленность. За один проход мы сможем проверить все возможные гипотезы относительно используемого кода и выяснить, какая из них наиболее подходит для расшифровки сообщения.
Для проверки осмысленности каждый из процессоров должен иметь доступ к словарю возможных в сообщении слов. Другой вариант – каждый из процессоров должен иметь свою копию словаря и обращаться к ней для осуществления проверки.
Теперь сделаем задачу интереснее. Предположим, что в начале нам известно всего несколько слов, которые составляют наш начальный словарь. При этом нам известны все ключи и правила перекодировки. Тогда в потоке сообщений мы сможем подобрать ключ только для тех сообщений, в которых будет хотя бы одно из известных нам слов.
Когда мы узнаем правильный код для немногих расшифрованных сообщений, мы получим правильное написание для других ранее неизвестных нам слов. Этими словами можно пополнить словарь того процессора, что нашел правильный ответ. Кроме того, новые слова можно передать всем остальным процессорам и пополнить и их локальные словари. По мере приобретения опыта мы будем расшифровывать все больший процент сообщений пока не получим полный словарь и близкую к ста процентам результативность расшифровки.
Возможны ситуации, когда сразу несколько ключей проявят в перекодированном сообщении слова, имеющиеся в словаре. В этом случае можно либо игнорировать такие сообщения, считая их нерасшифрованными, либо выбирать тот ключ, который дает большее количество совпадений слов из нашего словаря. Возможны и случайные появления осмысленных слов, тогда придется вводить для новых слов признак «предположительно» и менять его на признак «подтверждено», когда такое слово встретится в расшифрованных текстах неоднократно.
Получившаяся простая криптографическая система интересна тем, что позволяет ввести понятие «смысл», близкое по сути к тому, что мы обычно называем смыслом, и дать алгоритм, позволяющий с ним работать.
Результат раскодирования, полученный с неким ключом, можно назвать интерпретацией или трактовкой исходного кодированного текста в контексте этого ключа. Алгоритм определения криптографического смысла – это проверка всех возможных кодовых интерпретаций и выбор такой, которая выглядит наиболее правдоподобно с точки зрения памяти, которая хранит весь предыдущий опыт интерпретаций.
Смысл информации
Интерпретацию смысла и алгоритм его определения, введенные для криптографической задачи, можно расширить для более общего случая произвольных информационных сообщений, составленных из дискретных элементов.
Введем термин «понятие» – c (concept). Будем полагать, что всего нам доступно N понятий. Набор всех доступных понятий образует словарь
Будем называть информационным сообщением длины k набор понятий
Будем полагать, что сообщению может быть поставлена в соответствие его трактовка Iint (interpretation). Трактовка сообщения – это также информационное сообщение, состоящее из понятий множества C.
Введем правило получения трактовок. Будем полагать, что любая трактовка получается заменой каждого понятия исходного сообщения на некое другое понятие или на само себя. При этом первое понятие сообщения переходит в первое понятие трактовки и так далее.
Допустим, что в том, какие замены осуществляются при трактовке, есть определенная система, которая в общем случае нам неизвестна.
Введем понятие «субъект» S. Для субъекта определим его память, то есть персональный опыт как набор известной ему информации, получившей трактовку. Информация в купе с трактовкой может быть записана парой
Тогда память может быть записана как множество всех таких пар
Допустим, что есть учитель, который готов для каждого сообщения предоставить его правильную трактовку. Проведем стадию начального обучения, используя возможности учителя. Будем запоминать сообщения и трактовки данные учителем, как пары вида «сообщение – трактовка».
На основе памяти, сформированной с учителем, мы можем попытаться найти систему в сопоставлении понятий и их трактовок. Самое простое, что мы можем сделать — это для каждого понятия собрать все его возможные трактовки, что хранятся в памяти, и получить спектр возможных значений понятия. По частоте использования той или иной трактовки можно дать оценку вероятности соответствующего толкования.
Но чтобы, действительно, найти систему в сопоставлении нам необходимо каким-либо разумным методом решить задачу кластеризации и поделить объекты mi на классы по тому критерию, как происходит внутри класса трактовка одних и тех же понятий. Будем стараться сделать так, чтобы для всех объектов внутри одного класса действовали одни и те же правила трактовки входящих в них понятий. То есть, если для одного воспоминания, отнесенного к конкретному классу, некое понятие переходит в определенную трактовку, то в эту же трактовку оно будет переходить и во всех остальных воспоминаниях этого класса.
Обратите внимание, на особенность проводимой кластеризации. Расстояние между воспоминаниями вычисляется не по схожести исходных описаний или полученных трактовок, а по тому насколько похожие правила использовались при получении трактовки из исходного описания. То есть, объединяются в классы не воспоминания внешне похожие друг на друга, а воспоминания для которых оказались общими правила интерпретации, входящих в них понятий.
Будем называть классы, полученные в результате такой кластеризации, «контекстами» — Context.
Совокупность всех контекстов для субъекта S образует пространство контекстов
{Contexti| i=1...NContext}.
Для каждого i контекста можно задать набор правил трактовки понятий
Набор правил для контекста — это множество пар «исходное понятие — трактовка», описывающих все преобразования, свойственные контексту.
После завершения стадии первичного обучения можно ввести алгоритм, позволяющий трактовать новую информацию. Выделим из памяти M память Mint, состоящую исключительно из трактовок
Введем меру согласованности трактовки и памяти трактовок. В простейшем случае это может быть число совпадений трактовки и элементов памяти, то есть то, сколько раз именно такая трактовка встречается в памяти трактовок

Теперь для любой новой информации I мы можем для каждого контекста Contextj получить трактовку Ijint, применив к исходной информации правила преобразования Rj. Далее для каждой получившейся трактовки можно определить ее согласованность с памятью трактовок
Схема вычислений для одного контекста показана на рисунке ниже.

Вычислительная схема одного контекстного модуля
Введем вероятность трактовки информации в контексте j

В результате мы получим трактовку информации I в каждом из K возможных контекстов и вероятность этой трактовки
Если все вероятности равны нулю, то мы констатируем, что информация субъектом не понята и не имеет для него смысла. Если же есть вероятности, отличные от нуля, то соответствующие им трактовки образуют множество возможных смыслов информации.
Если мы решим определиться с одной главной интерпретацией информации для данного субъекта, то можно воспользоваться контекстом с максимальным значением вероятности.
Как правило, информация содержит не один, а несколько смыслов. Дополнительные смыслы можно выделить, если взять отличные от главного контексты трактовки с ненулевой вероятностью. Но в этой процедуре есть свои подводные камни. При выборе надо учитывать возможную коррелированность контекстов. Позже мы рассмотрим это подробнее.
В итоге, понятие «смысл» можно описать следующим образом. Смыслом определенной информации для конкретного субъекта является набор трактовок, наиболее удачных в плане соответствия этих трактовок и памяти субъекта, полученных в результате анализа информации в различных контекстах, построенных, в свою очередь, на опыте этого субъекта.
Общая схема вычислений, связанных с определением смысла, может быть изображена как совокупность работающих параллельно контекстных вычислительных модулей (рисунок ниже). Каждый из модулей осуществляет трактовку исходного описания по своей системе правил преобразования. Память всех модулей одинакова по своему содержанию. Сравнение с памятью дает оценку соответствия трактовки и опыта. Исходя из вероятностей трактовок осуществляется выбор конкретного смысла. Процедура повторяется до тех пор пока не исчерпаются основные смысловые интерпретации информации.

Вычислительная схема определения одного из смыслов в системе с K контекстами
После того, как определился смысл информации, можно дополнить память новым опытом. Этот новый опыт можно использовать для определения трактовки последующей информации и для уточнения пространства контекстов и правил преобразования. Таким образом можно не выделять отдельную стадию начального обучения, а просто накапливать опыт, улучшая при этом способность вычленения смысла.
Описанный подход, связывающий информацию и ее смысл, содержит несколько ключевых моментов:
- Информационные описания, к которым применим такой подход, строятся из дискретных (номинальных) понятий. Это определяется идеологией сопоставления понятий и их трактовок в определенном контексте.
- Опыт позволяет сформировать пространство контекстов и правила трактовки в этих контекстах. Соответственно, смысл может быть определен субъектом только при наличии определенного опыта.
- Поскольку опыт различных субъектов может быть различен, могут различаться и смыслы, полученные в результате восприятия одной и той же информации;
- Информация может быть специально подготовлена отправителем таким образом, чтобы максимизировать вероятность появления у получателя определенного смысла;
- Не стоит говорить о том, что информация содержит смысл независимо от воспринимающего субъекта. Смысл – это результат «измерения» информации, выполненный субъектом. До момента определения смысла, для конкретного субъекта информация содержит трактовки сразу во всех контекстах, для которых оказалась ненулевая вероятность этих трактовок. Каждое «измерение» позволяет увидеть один из возможных смыслов. Этот пункт, кстати, повторяет копенгагенскую трактовку состояния квантовой системы и момента измерения.
Проблема перебора
Описанный алгоритм определения смысла очень тесно связан с вопросом о равенстве классов P и NP, который так же известен как проблема перебора. Нестрого проблему перебора можно описать так: если есть вопрос и есть ответ на этот вопрос, и можно быстро проверить правильность этого ответа (за полиномиальное время), то можно ли так же быстро найти на этот вопрос правильный ответ (за полиномиальное время и используя полиномиальную память).
Например, допустим, что у нас есть таблица простых чисел, некое число и утверждение, что определенный набор простых чисел является разложением этого числа. Чтобы проверить это утверждение достаточно перемножить простые числа из предлагаемого набора и посмотреть, получится ли в результате наше число. Но если мы просто захотим найти разложение этого числа на простые множители, то столкнемся с необходимостью перебора всех простых сомножителей. С ростом разрядности исходного числа количество простых чисел, которые требуется перебрать, растет экспоненциально. Соответственно, решение, основанное на переборе, оказывается экспоненциально сложным по отношению к линейному росту сложности условия. Вопрос о равенстве классов P и NP — это вопрос о том, существует ли для этой и других сложных, основанных на переборе, задач алгоритмы, способные решать их за полиномиальное от сложности входных данных время и память. Если любую “сложную” задачу можно свести к “простой”, то классы равны.
На сегодня вопрос о равенстве классов открыт, но большинство математиков склоняется к тому, что эти классы все-таки не равны. Так как работа всех алгоритмов шифрования с открытым ключом основана на том, что есть нечто, что легко проверить, но трудно найти, то это значит, что по мнению большинства математиков криптография может быть надежной.
В нашем случае мы имеем набор понятий, описания составленные из этих понятий и некий опыт обучения, когда нам указываются правильные трактовки для некоторых описаний.
Исходя из данных обучения мы можем составить спектры возможных трактовок. То есть для каждого понятия посмотреть, какие трактовки оно принимало и предположить, что других трактовок для него не бывает.
Теперь можно попробовать дать трактовку какому-либо описанию. Предположим, что у нас есть огромный опыт и в используемой нами памяти есть все возможные корректные трактовки для любых описаний. Тогда можно составить из спектров трактовок, допустимых для понятий, входящих в описание, все возможные совместные комбинации и посмотреть, не окажется ли какая-нибудь из них похожа на содержимое памяти. Так как наша память огромна, то там обязательно найдется совпадение (если, конечно, исходная фраза корректна). Если оно будет единственным, то это и будет правильная трактовка исходного описания.
Количество комбинаций, которые потребуется перебрать, будет равно произведению размеров спектров всех понятий исходного описания. Например, для описания из 10 понятий при 10 возможных трактовках для каждого понятия мы получим 10 миллиардов вариантов. С ростом длины описания и количеством трактовок, имея экспоненциальный рост, мы получим так называемый комбинаторный взрыв.
Можно провести приблизительную аналогию с переводом с одного языка на другой. Имея образцы текстов и их переводов можно для каждого слова составить спектр его возможных переводов на другой язык. Условно правильным вариантом перевода (не будем брать в расчет ничего кроме перевода самих слов) будет одна из комбинаций, составленная из спектров возможных переводов отдельных слов. Для реального языка в большинстве случаев мы получим сотни миллионов, триллионы или более комбинаций. При этом потребуется база всех корректных предложений. Можете представить ее размер.
Контекстный подход позволяет значительно упростить вычисления за счет выделения закономерностей в системе трактовок. Если есть некие общие правила сопоставления понятий и их трактовок, то наблюдение за корректными примерами трактовки позволяет выделить эти правила. Области действия общих правил мы назвали контекстами. Для проверки гипотез о возможной трактовке входной информации теперь достаточно проверить только те интерпретации, что возникают в контекстах.
Количество необходимых контекстов определяется природой входной информации и той точностью понимания смысла, которую мы хотим получить. Для практических задач для получения хороших результатов почти всегда оказывается достаточно не более миллиона контекстов, при том, что общее число комбинаций может быть выше на много порядков.
Если продолжить пример с переводом, то контекстный подход говорит о том, что можно выделить фиксированное число смысловых контекстов, внутри которых перевод для многих слов окажется согласован между собой. Например, если удается определить, что текст носит научный характер, то из спектра возможных трактовок многих слов уйдут практически все варианты, кроме одного. Аналогично и с другими тематиками.
Определить то, какому контексту при переводе стоит отдать предпочтение, можно по тому, в каком контексте трактовка фразы выглядит правдоподобнее. В том числе исходя из того, насколько часто фразы с таким набором слов встречаются в этом контексте. В том, что описано, можно усмотреть много общего с теми методами, что используются в реальных системах перевода, что и неудивительно.
Фреймы
Описываемая контекстно-смысловая модель, во многом, решает те же задачи, что и концепция фреймов Марвина Минского («A Framework for Representing Knowledge», Marvin Minsky). Общие задачи, которые стоят перед моделями, неизбежно приводят к похожим реализациям. Описывая фреймы, Минский использует термин «микромиры», понимая под ним ситуации, в которых существует определенная согласованность описаний, правил и действий. Такие микромиры можно сопоставить с контекстами в нашем определении. Выбор наиболее удачного фрейма из памяти и его приспособление к реальной ситуации также может быть во многом сопоставлен с процедурой определения смысла.
При использовании фреймов для описания зрительных сцен, фреймы трактуются, как различные «точки зрения». При этом разные фреймы имеют общие терминали, что позволяет координировать информацию между фреймами. Это соответствует тому, как в разных контекстах правила трактовки могут привести разные исходные описания к одним и тем же описаниям-трактовкам.
Популярный в программировании объектно-ориентированный подход, непосредственно связанный с теорий фреймов, использует идею полиморфизма, когда один и тот же интерфейс при применении к объектам различных типов вызывает разные действия. Это достаточно близко к идее трактовки информации в соответствующем контексте.
При всей похожести подходов, связанной с необходимостью отвечать на одни и те же вопросы, контекстно-смысловой механизм существенно отличается от теории фреймов и, как будет видно дальше, не сводится к ней.
Особенность контекстно-смыслового подхода заключается в том, что он одинаково хорошо применим ко всем видам информации, с которыми сталкивается и оперирует мозг. Различные зоны коры реального мозга крайне похожи с точки зрения внутренней организации. Это заставляет думать, что все они используют один и тот же принцип обработки информации. Очень похоже, что на роль такого единого принципа может претендовать подход, связанный с выделением смысла. Попробуем на нескольких пимерах показать основыне идеи применения смыслового механизма.
Семантическая информация
Слова, из которых строятся фразы, могут быть по-разному истолкованы в зависимости от общего контекста повествования. Однако для каждого слова можно составить спектр значений, описанный в других словах. Если проследить за тем от чего зависит разная трактовки одних и тех же слов, то можно выделить тематические области трактовки. Внутри таких областей многие слова будут иметь однозначный определенный темой области смысл. Набор таких тематических областей и есть пространство контекстов. Контексты могут быть связаны с временем повествования, числом, родом, предметной областью, тематикой и так далее.
Похожая ситуация, связанная с выбором возможной трактовки для каждого из слов фразы, возникает при переводе с одного языка на другой. Возможные варианты перевода какого-либо слова наглядно показывают спектр возможных значений этого слова (рисунок ниже).

Пример спектра возможных трактовок, возникающих при переводе
Определение смысла фразы – это выбор такого контекста и получение таких трактовок слов, которые создают предложение наиболее правдоподобное, исходя из опыта того, кто этот смысл пытается понять.
Возможны ситуации, когда одна и та же фраза в разных контекстах создаст разные трактовки, но при этом эти трактовки будут допустимы, исходя из предыдущего опыта. Если стоит задача определить единственный смысл такой фразы, то можно выбрать ту трактовку, у которой выше совпадение с памятью и, соответственно, рассчитанная для нее вероятность. Если же фраза изначально составлена как двусмысленная, то уместно воспринять каждый из смыслов по отдельности и констатировать тот факт, что автору фразы вольно или невольно удалось их совместить в одном высказывании.
Естественный язык является мощным инструментом выражения и передачи смысла. Однако эта мощность достигается за счет нечеткости трактовок и их вероятностного характера, зависящего от опыта воспринимающего субъекта. В большинстве бытовых ситуаций этого вполне достаточно для краткой и достаточно точной передачи смысла.
Когда передаваемый смысл достаточно сложен, как это бывает достаточно часто, например, при обсуждении научных или юридических вопросов, имеет смысл переходить на использование специальных терминов. Переход на терминологию – это выбор собеседниками такого согласованного контекста, в котором слова-термины трактуются собеседниками одинаково и однозначно. Чтобы такой контекст оказался доступен обоим собеседникам, каждому из них необходим соответствующий опыт. Для одинакового понимания опыт должен быть схож, что достигается за счет соответствующего обучения.
Для естественного языка можно использовать меру согласованности контекста и памяти, основанную не только на полном совпадении описаний, но и на схожести описаний. Тогда становится доступно большее количество возможных смыслов и появляется возможность дополнительной трактовки фраз. Например, таким образом можно корректно трактовать фразы, содержащие ошибки или внутренние противоречия. Или сказанные образно, или в переносном смысле.
При определении смысла легко учитывать общий контекст повествования. Так, если фраза допускает толкования в разных контекстах, предпочтение стоит отдавать контекстам, которые были активны у предыдущих фраз и задавали общий контекст. Если же фраза допускает толкование только в контексте, отличном от основного повествования, то это стоит воспринимать, как переключение повествования на другую тему.
Аудиальная информация
Аналоговый звуковой сигнал легко преобразуется в дискретную форму. Для этого сначала выполняется дискретизация по времени, когда непрерывный сигнал заменяется замерами, выполненными с частотой дискретизации. Затем проделывается квантование амплитуды. При этом уровень сигнала заменяется на номер ближайшего уровня квантования.
Полученную запись сигнала можно разбить на временные интервалы и выполнить для каждого из них оконное преобразование Фурье. В результате получится запись звукового сигнала в виде последовательности спектральных замеров (рисунок ниже).
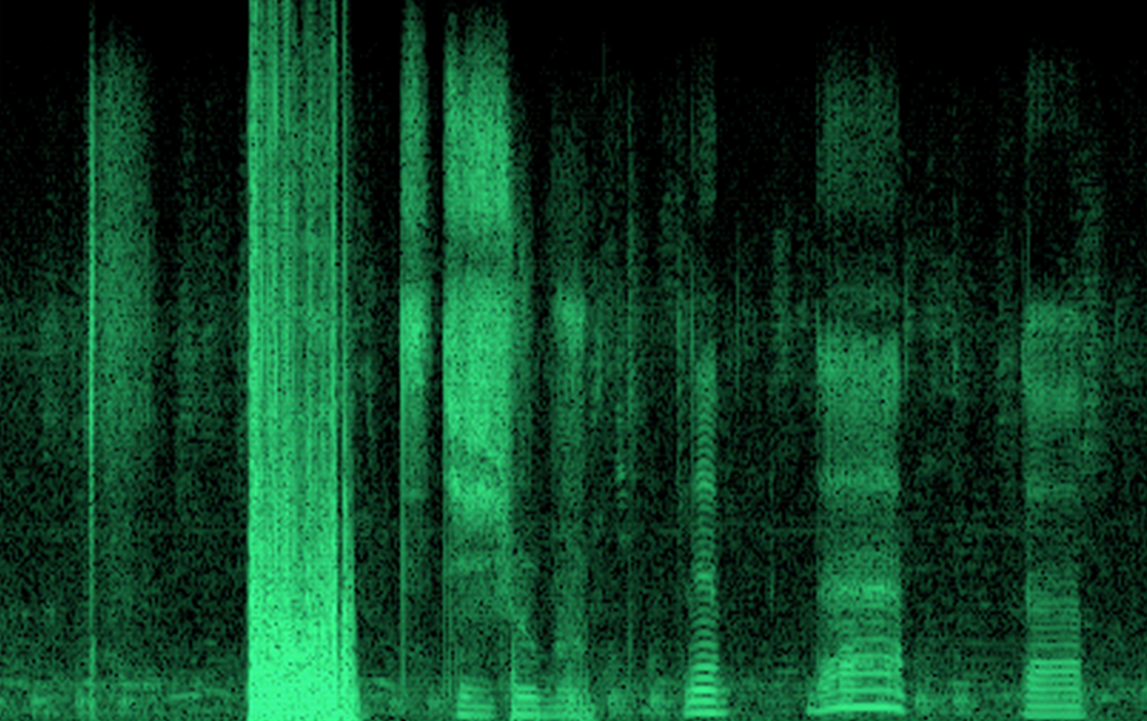
Пример временной развертки спектра речевого сигнала
Введем для временных интервалов кольцевой идентификатор с периодом NT. То есть занумеруем первые NT интервалов от 1 до NT. NT+1 интервал опять занумеруем 1 и так далее. В результате мы получим одинаковые номера через каждые NT интервалов.
Предположим, что преобразование Фурье содержало NF частотных интервалов. Это значит, что каждый спектральный замер будет содержать NF комплексных значений. Каждое комплексное значение заменим на его амплитуду и фазу и выполним их квантование. Амплитуду с NA уровнями квантования, фазу с NP уровнями.
Внутри диапазона из NT временных интервалов каждый элемент записи спектра можно описать сочетанием: код временного интервала, значение частоты, значение амплитуды, значение фазы. Ведем набор понятий C, позволяющий описать звук внутри интервала, заданного периодом кольцевого идентификатора. Это будут все возможные сочетания
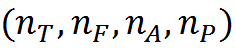
Всего таких понятий будет
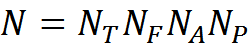
Соответственно, набор понятий C будет содержать N элементов

Любой звуковой сигнал продолжительностью не более NT временных интервалов можно записать как информацию через перечисление таких понятий.
 , где ij∈C
, где ij∈CС помощью этих же понятий можно записать и любую трактовку.
Если посмотреть на картинку с записью спектра речевого сигнала, то каждое из таких звуковых понятий — это точка с определенными координатами и яркостью. Есть еще фаза, но она на картинке не видна. Имея набор всех точек со всеми возможными цветами (амплитудами), мы, естественно, можем нарисовать любую картинку.
Задача распознавания звуковых образов требует узнавания одного и того же звукового образа при условии, что текущее звучание может быть трансформировано по отношению к тому, что хранится в памяти. Основные звуковые трансформации — это изменение громкости, изменение тональности звучания, изменение темпа звучания и сдвиг начала звучания.
Этим трансформациям соответствуют:
- Изменение амплитуды;
- Смещение по частоте;
- Линейное изменение временного масштаба;
- Сдвиг по временной шкале.
Введем пространство контекстов, покрывающее возможные сочетания трансформаций. Для каждого контекста можно создать правила переходов, то есть описать, как будет выглядеть каждое из исходных понятий в контексте соответствующего преобразования. Например, при контексте изменения частоты на одну позицию вверх все понятия получат трактовку, сдвигающую их на одну позицию вниз. Чистый тон на частоте 1 кГц – это то же, что и тон на частоте 900 Гц при контексте общего сдвига звучания вверх на 100 Гц. Аналогично с остальными видами трансформаций.
После описания правил переходов понятий в различных контекстах окажется возможным узнавать одни и те же звуковые образы независимо от их трансформаций. Момент произнесения, громкость, высота голоса и скорость речи не будут влиять на возможность сравнения текущей информации с той, что хранится в памяти. Текущее звучание будет преобразовано в различные трактовки во всех возможных контекстах. В том контексте, который соответствует искомой трансформации, описание примет трактовку, в которой можно легко узнать что-то уже слышанное ранее.
На практике при работе со сложными сигналами, например, с речью, оказывается невозможно обойтись одним этапом обработки. Сначала целесообразно ограничиться выделением простых фонем. Контексты при этом будут содержать правила трансформаций элементарных звуков, как описано выше. Затем составить описание, состоящее из фонем. При этом фонема будет достаточно сложным элементом, идентифицирующим не только звуковую форму, но и ее высоту, временное положение и скорость произнесения. Информация, составленная из фонем, в свою очередь, может быть подвергнута последующей обработке на новом пространстве контекстов.
Контексты можно усложнять, не ограничиваясь только простыми трансформациями. При этом само определение подходящего контекста создает дополнительную информацию. Например, для речи контекстами являются различные интонации и языковые акценты. Интонационные и акцентные контексты позволяют не только повысить точность распознавания, но и получить дополнительные знание о том, как именно сказана фраза.
Визуальная информация
Рассмотрим наиболее простые способы работы с изображением. Предположим, что у нас есть растровая картинка, состоящая из точек, для которых задан их цвет. Переведем изображение в черно-белое, оставив только значения яркости точек. Выполним выделение контура изображения (например, при помощи алгоритма Кэнни (JOHN CANNY, A Computational Approach to Edge Detection) (рисунок ниже)).


Результат выделения границы
Теперь разобьем изображение на небольшие квадратные области. В каждой небольшой области, через которую проходит линия границы, эта линия может быть аппроксимирована отрезком прямой. Зададимся числом квантования ориентации NO и определим соответствующие направления. Теперь для каждого квадрата, если он содержит границу, можно указать номер направления, наиболее точно соответствующего ориентации границы. Можно ввести и более сложные и, соответственно, более точные описания, но для примера нам подойдет и такая упрощенная модель.
Предположим, что размеры сетки, делящей изображение на области, NX на NY. Введем набор понятий C в который войдут понятия, соответствующие всем возможным сочетаниям

Таких понятий будет

Соответственно информационное описание изображения можно свести к перечислению соответствующих ему понятий
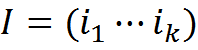 , где ij∈C
, где ij∈CТеперь нас будет интересовать задача инвариантного узнавания изображений. Зададимся набором трансформаций, по отношению к которым мы хотим добиться инвариантности. Наиболее распространенные на практики трансформации:
- горизонтальный сдвиг;
- вертикальный сдвиг;
- поворот;
- общее изменение масштаба;
- растяжение/сжатие по X;
- растяжение/сжатие по Y.
Эти преобразования наиболее интересны, так как соответствуют тому, как меняется проекция плоской фигуры при ее пространственных перемещениях и поворотах.
Теперь создадим пространство контекстов. Для этого осуществим квантование параметров трансформаций, то есть разобьем их на дискретные значения. И создадим столько контекстов, сколько возникнет возможных сочетаний этих параметров.
Для каждого контекста можно описать правила преобразования понятий. Так, вертикальная линия перейдет в горизонтальную при повороте на 90 градусов, вертикальная линия в позиции (0,0) станет вертикальной линией в позиции (10,0) при горизонтальном сдвиге на 10 позиций и так далее.
После задания правил трансформаций достаточно один раз увидеть и запомнить какой-либо образ, чтобы при предъявлении его в трансформированном виде определить и образ, и тип трансформации. Каждый контекст выполнит преобразование описания в трактовку, характерную для этого контекста, то есть совершит геометрическое преобразование описания, после чего сравнит с памятью на предмет поиска соответствия. Если такую проверку вести параллельно во всех контекстах, то за один такт можно найти смысл исходной информации. В данном случае это будет узнавание образа, если он нам был знаком, и определение его текущей трансформации.
Можно не ограничиваться описанными преобразованиями. Можно использовать, например, трансформацию «изгиба листа» и тому подобное. Но увеличение количества трансформации ведет к экспоненциальному росту количества контекстов. На практике задача обработки изображений описанным методом допускает очень сильные оптимизации, что позволяет производить расчеты в реальном времени. Основанные на таких идеях, но более продвинутые алгоритмы будут подробно описаны позже.
Основная идея описанного подхода заключается в том, что для получения инвариантного представления какого-либо объекта не обязательно проводить длительное обучение, показывая этот объект в различных ракурсах. Гораздо эффективнее научить систему правилам основных геометрических преобразований, свойственных этому миру и единых для всех объектов.
Частично описанный подход реализуется в хорошо себя зарекомендовавших сверточных сетях (Fukushima, 1980) (Y. LeCun and Y. Bengio, 1995). Для получения инвариантности к сдвигу в сверточных сетях ядро свертки, описывающее искомый образ, примеряется ко всем возможным позициям по горизонтали и вертикали. Такая процедура повторяется для всех знакомых сети образов с целью определения наиболее точного соответствия (рисунок ниже). По сути этот алгоритм декларирует «зашитое» в него априори знание о правилах трансформации при горизонтальном и вертикальном сдвиге. Используя эти знания, он формирует пространство возможных контекстов, реализуемое слоями простых искусственных нейронов. Определение максимального совпадения при свертке для различных ядер аналогично описанному нами определению смысла.
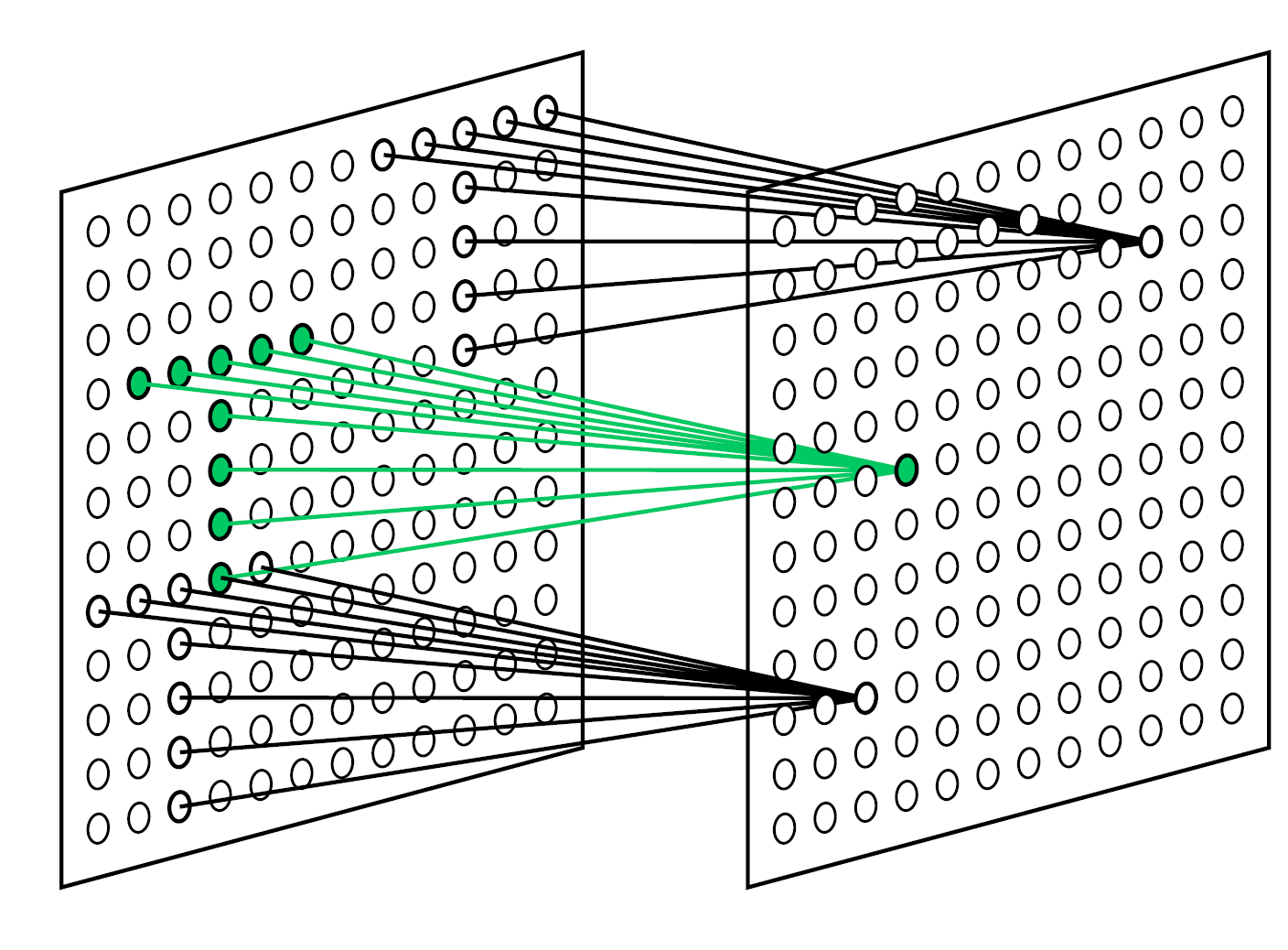
Рецептивные поля простых клеток, настроенных на поиск выбранного паттерна в разных позициях (Fukushima K., 2013)
Функция соответствия и условия выбора лучшего контекста
Функция соответствия трактовки и памяти служит для определения вероятности реализации контекста, соответствующего этой трактовке. По тому, как наш мозг выбирает смысл в реальных ситуациях, можно предположить, что алгоритмы определения соответствия могут быть достаточно сложны и не сводиться к одной простой формуле.
Ранее мы привели для примера «жесткую» функцию соответствия, основанную на точном совпадении описаний. Для памяти интерпретаций

Функция соответствия

Введем меру сравнения описаний Q. Меру, основанную на точном совпадении можно записать

Функция соответствия примет вид
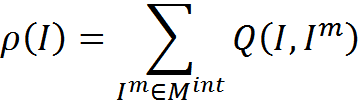
Соответствие, основанное на точном совпадении, позволяет определить смысл только в том случае, если хотя бы в одном контексте найдется интерпретация, уже хранящаяся в памяти. Но можно представить ситуацию, когда уместно найти наиболее подходящий контекст для трактовки описания, даже при отсутствии точных совпадений. В этом случае можно воспользоваться менее строгим сравнением описаний. Например, можно ввести меру схожести описаний, основанную на количестве общих для двух описаний понятий.
Ранее мы уже говорили о возможности кодирования описаний через сложение битовых массивов в фильтр Блума (Bloom, 1970). Сопоставим каждому понятию из словаря С его разряженный бинарный код длины m, содержащий k единиц.


Тогда каждому описанию I, состоящему из n понятий, можно сопоставить бинарный массив B, полученный от логического сложения кодов понятий, входящих в описание.

О похожести двух описаний можно судить по схожести их бинарных представлений. В нашем случае уместной выглядит мера сходства, основанная на их скалярном произведении.
Скалярное произведение двух бинарных массивов показывает сколько единиц совпало в этих двух массивах. Всегда есть вероятность того, что единицы в бинарных описаниях совпадут случайно. Ожидание количества случайно совпавших единиц M зависит от длины бинарного кода, количества единиц, кодирующих одно понятие, и количества понятий в описаниях. Чтобы избавиться от случайной составляющей, меру сходства можно скорректировать на величину случайного ожидания.

Такая мера может принимать отрицательные значения, которые сами по себе не имеют смысла. Но при сложении мер близости для всех элементов памяти они позволят компенсировать случайные положительные выбросы. Тогда функцию соответствия можно записать

При «мягком» задании функции соответствия наша модель уходит в сторону статистической оценки вероятностей того или иного контекста и может быть сопоставлена с Байесовскими методами, скрытыми Марковскими моделями и методами нечеткой логики.
«Жесткий» и «мягкий» подходы имеют, как свои плюсы, так и свои минусы. Мягкий подход позволяет получить результат для информации, которая не имеет четкого аналога в памяти. Это может быть в случаях, когда само описание содержит неточности или ошибки. В таких случаях, определив предпочтительный контекст, можно в качестве трактовки использовать наиболее похожее корректное воспоминание.
Кроме того, мягкое сравнение дает результат, когда описания, хранящиеся в памяти, содержат несущественные для смысла подробности, которые можно считать информационным шумом. Однако жесткий подход может давать принципиально более качественный результат. В большинстве случаев попадание в редкую, но адекватную для описания трактовку, значительно предпочтительнее шаблонных трактовок, основанных на «внешнем» сходстве.
Еще один, пожалуй, самый интересный подход возможен, если в наборе всех описаний предварительно выделить факторы, отвечающие за некие сущности, общие для части описаний. Тогда можно строить функцию соответствия, как мягкое или жесткое сравнение с портретами факторов. Такой подход хорош тем, что позволяет однозначно или с определенной вероятностью определять присутствие факторов на фоне зашумленной другими описаниями информации.
Разумным видится комбинированный подход, использующий все виды оценок соответствия. Самое главное, что определение смысла не является замкнутой в себе операцией. Правильное определение смысла служит основой для последующих информационных операций, связанных с мышлением и поведением субъекта. Как будет показано дальше, алгоритмы поведения и мышления определяется механизмами обучения с подкреплением, которые позволяют сформировать наиболее адекватные к ситуации мыслительные ходы и поведенческие акты. Можно предположить, что и с определением смысла наилучшим результатом будет не некая жестко заданная стратегия расчета функции соответствия, а расчет на основе обучения с подкреплением, который будет оптимизировать функцию расчета, исходя из успешности опыта предыдущих оценок.
В следующей части я покажу, как, возможно, работает со смыслом реальный мозг и расскажу, как с помощью паттерно-волновая модели, голографической памяти и понимания роли миниколонок кортекса можно попробовать обосновать, как выглядит пространство контекстов, реализованное на биологических нейронах.
Алексей Редозубов
Логика сознания. Вступление
Логика сознания. Часть 1. Волны в клеточном автомате
Логика сознания. Часть 2. Дендритные волны
Логика сознания. Часть 3. Голографическая память в клеточном автомате
Логика сознания. Часть 4. Секрет памяти мозга
Логика сознания. Часть 5. Смысловой подход к анализу информации
Логика сознания. Часть 6. Кора мозга как пространство вычисления смыслов
Логика сознания. Часть 7. Самоорганизация пространства контекстов
Логика сознания. Пояснение «на пальцах»
Логика сознания. Часть 8. Пространственные карты коры мозга
Логика сознания. Часть 9. Искусственные нейронные сети и миниколонки реальной коры
Логика сознания. Часть 10. Задача обобщения
Логика сознания. Часть 11. Естественное кодирование зрительной и звуковой информации
Логика сознания. Часть 12. Поиск закономерностей. Комбинаторное пространство
Логика сознания. Часть 13. Мозг, смысл и конец света
