Эффективный расчёт области видимости и линии взгляда в играх

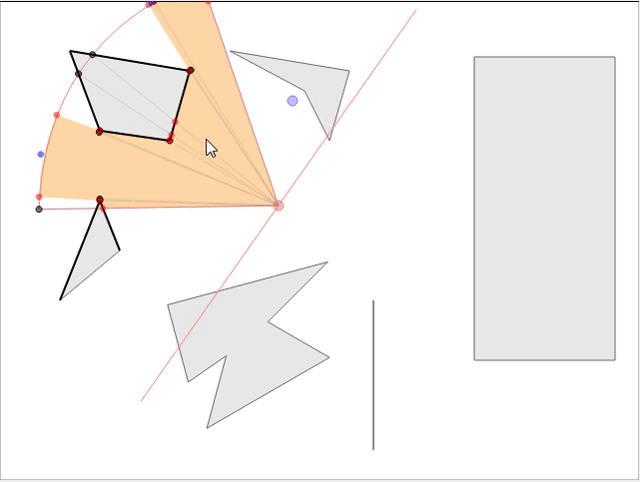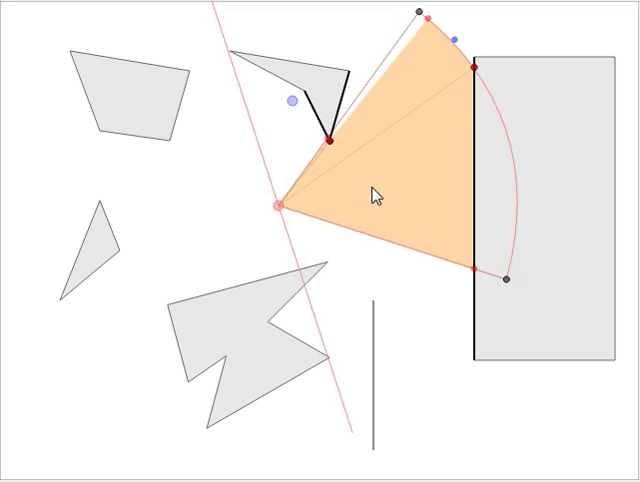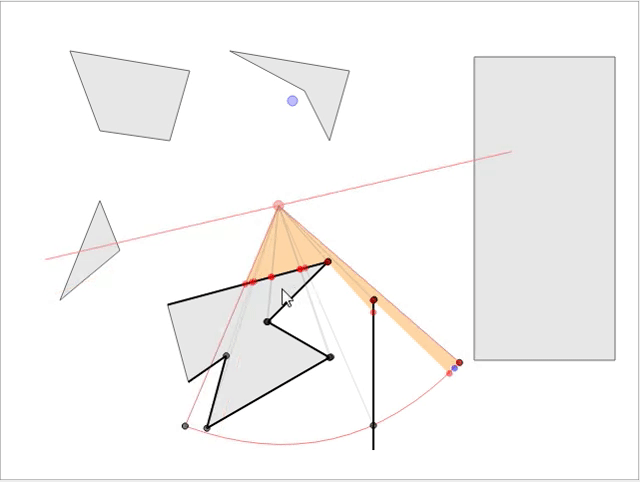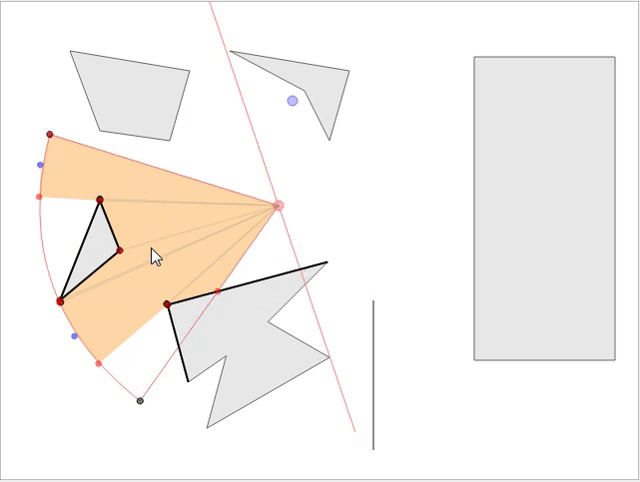
В стратегических играх обычно требуется знать область видимости NPC, чтобы игрок мог продумывать стратегию и делать следующий ход. Мы рассмотрим математику и реализацию рациональной модели, не просаживающей скорость игры при большом количестве NPC на карте. Если вы хотите увидеть готовое интерактивное демо модели, перейдите сюда и играйте прямо в браузере! Вот скриншот демонстрации:



Имея параметры видимости наблюдателя (направление взгляда, расстояние видимости и угол поля зрения), нам нужно найти видимую для него область, т.е. определить область видимости (field of view, FoV). Если препятствия отсутствуют, это будет сектор круга, состоящий из двух граней (радиусов) и соединяющей их дуги (см. Рис. 1). Кроме того, имея заданную точку мира, мы должны быстро определить, видима ли она для наблюдателя, т.е. необходимо обрабатывать запросы линии взгляда (line of sight, LOS) для заданной точки. Обе эти операции можно выполнить достаточно эффективно для использования при рендеринге в реальном времени.


Рис. 1

Положение наблюдателя представлено красной точкой, стрелкой указано направление взгляда, r — это расстояние видимости, а θ — половина угла поля зрения.

1 Входные данные

• Набор полигонов, в том числе и границы мира
• Параметры FoV
  
  • Положение наблюдателя
  • Направление взгляда, V
  • Угол поля зрения, 2θ < 180°
  • Расстояние видимости, r

Примечание: здесь и ниже буквы в нижнем регистре обозначают скалярные значения, а в верхнем — векторные.

1.1 Полигоны и рёбра

При описании мира в 2D здания естественным образом разбиваются на полигоны и таким образом становятся входными данными алгоритма. Однако технически область зрения ограничивается стенами, т.е. рёбрами полигонов. Кроме того, работа с рёбрами полигонов обеспечивает улучшенные детализацию и контроль, потому что при проверке пересечений мы в основном будем иметь дело с геометрическими примитивами. Поэтому в большинстве случаев алгоритм работает непосредственно с рёбрами и не касается абстракций более высокого уровня (полигонов).

2 Базовый алгоритм

Первая приходящая в голову интересная идея — обрезка сектора видимости контурами полигонов. Но мы рассматриваем видимость, и попытка решения этой задачи обрезкой по контуру не сработает, конечный результат будет неверным. Это понятно, ведь обрезка только отсекает пересечение двух областей, а для видимости нам нужно отсечь не только пересечение, но и всё за ним по принципу радиальности. На Рис. 2 показан результат обрезки (слева) и ожидаемый для такой конфигурации результат (справа).


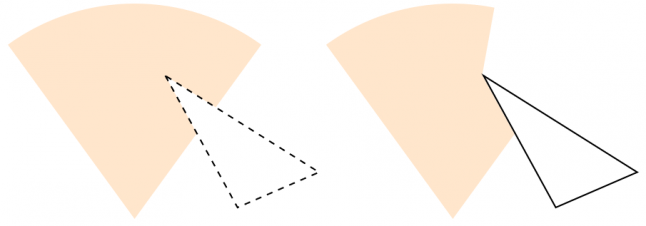
Рис. 2

В реальном мире мы видим объекты, когда световые лучи беспрепятственно попадают в глаз. Интуитивно понятно, что видимость можно определить обратной операцией, т.е. испусканием лучей из глаза в мир. В случае источника света лучи испускаются во всех направлениях. В практической реализации лучи испускаются радиально с заданным интервалом, например, один луч через каждые 5° и 72 луча для всей окружности. Луч должен двигаться, пока он не будет заблокирован ребром. Испускание лучей на все 360° и определение освещённой источником света области в 2D является решённой проблемой [1]. Точность этого способа зависит от интервала между испускаемыми лучами. Меньшие интервалы обеспечивают большую плотность распределения лучей.


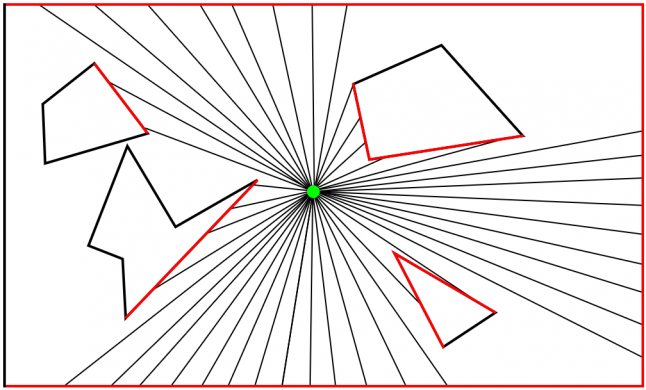
Рис. 3

Испускание лучей — это, иными словами, проверка на пересечение лучей с отрезками прямых. Для заданного луча при m отрезках выполняется m проверок для определения ближайшего к лучу ребра, блокирующего его. Поэтому в любом алгоритме отслеживания лучей для испускания n лучей на m рёбер необходимо выполнить n × m проверок. Однако, какой бы малой ни была ресурсоёмкость проверки пересечения лучей и отрезков прямых (рёбер), в огромном мире со множеством источников света такой подход может стать слишком затратным.

Давайте назовём блокирующее луч ребро блокирующим ребром. На Рис. 3 они выделены красным. Точку, в которой луч пересекает блокирующее ребро, назовём точкой попадания. После нахождения всех точек попадания их необходимо кругообразно соединить, т.е. все точки попадания упорядочиваются по углу и соединяются по линиям для определения области, освещённой источником света. Результатом будет неправильный замкнутый контур. Следует заметить, что при соединении точек пересечения таким образом некоторые углы или части полигонов отсекаются, что приводит к неверной или менее точной освещённой области. Её можно улучшить, уменьшив интервал испускания лучей. Чем меньше интервал, тем больше лучей и лучше покрытие. Результат улучается, но за счёт снижения производительности.

С помощью этой проблемы определения области освещённости мы рассмотрели основной подход, который мы будем использовать для решения нашей проблемы: метод отслеживания лучей (ray casting). Заметьте, что лучи света исходят из источника света во всех направлениях, пока не пересекутся с препятствием. Отсутствие ограничений делает проблему более простой по сравнению с нашей проблемой, в которой ограничены угол и расстояние видимости. Мы обсудим, почему это так, позже, в разделе 3.

2.1 Оптимизация

Вместо испускания лучей во всех направлениях (с определённым интервалом), задачу обычно оптимизируют испусканием лучей только в тех направлениях, в которых находятся концы рёбер. Это значительно снижает количество необходимых проверок пересечений. Вышеупомянутое значение n должно стать меньше. Ещё одно преимущество этого способа заключается в большей точности: теперь для правильности определяемой области видимости мы не полагаемся на выбранный интервал.


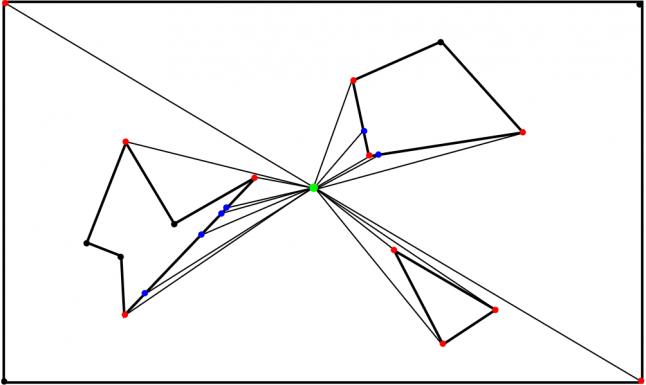
Рис. 4

Мы будем называть эти концы рёбер, дающие нам угол испускания лучей, угловыми точками. Это название вместо может показаться избыточным и бессмысленным, но позже оно нам пригодится. Угловые точки — это точки, в которые испускаются лучи видимости. На Рис. 4 угловые точки отмечены красным, синим и чёрным. Лучи испускаются во все эти точки. Точки, расположенные ближе всего к лучу, преобразуются в точки попаданий, отмеченные красным. Точки, которых не достигает их луч, отмечены чёрным. Эти лучи пересекаются с более близкими рёбрами и создают точки попаданий, отмеченные синим.

2.2 Зрение без углов

Хотя испускание лучей только в концы рёбер нас устраивает, у него есть небольшой недостаток. Заметьте, на Рис. 4 луч, испущенный к углу полигона, пересекает одно из рёбер, создающих угол, и не двигается дальше. Однако видимость должна в некоторых случаях быть дальше угла. Умный подход к решению этой проблемы показан в интерактивной статье [2].

Замысел в том, чтобы разделить первичный луч (луч на конце ребра) на два вспомогательных, отклонив их на угол «йота» по часовой и против часовой стрелки. Если видимость должна распространяться за угол, один из этих вспомогательных лучей пройдёт через угол, определив таким образом видимость за ним. Недостаток такого подхода: вместо одного луча нам теперь нужно испускать три для каждой угловой точки, что в три раза больше влияет на скорость. Было бы неплохо минимизировать количество угловых точек, которые нам нужно обработать.


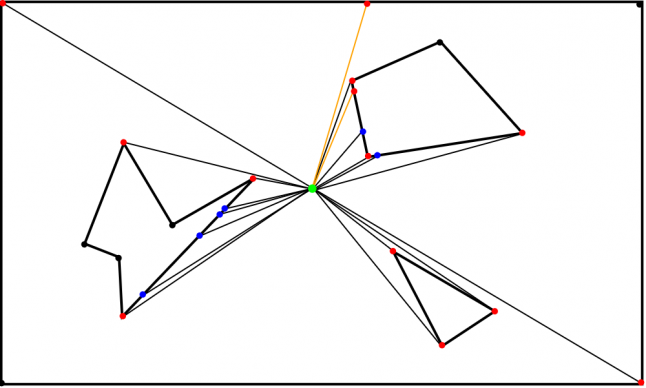
Рис. 5

Вспомогательные лучи выделены оранжевым. Угол отклонения (между оранжевым и чёрным лучом) здесь намеренно преувеличен для ясности, но он должен быть намного меньше, скажем, полградуса.

Простой оптимизацией стало бы определение того, видны ли оба ребра, формирующие угол, или одно из них скрыто другим. Если видны оба, то вспомогательные лучи не требуются, ведь видимость не может распространяться дальше. На Рис. 4 вершина треугольника — это видимый угол, вспомогательные лучи здесь не нужны, ведь видимость не может распространяться дальше. Вспомогательные лучи нужны только когда одно из двух рёбер скрыто от наблюдателя. Оба ребра не могут быть скрыты, потому что мы смотрим на каждый угол полигона в отдельности — на два ребра и точку, в которой они соединяются (см. Рис. 6, чёрные стрелки и синяя точка). Даже если одно из рёбер скрыто, испускание двух вспомогательных лучей избыточно; одного можно избежать, потому что только один может беспрепятственно пройти за угол. На Рис. 5 вспомогательный луч, созданный вращением первичного по часовой стрелке, избыточен.


Рис. 6

Для определения того, блокирует ли одно из рёбер другое, можно использовать теорему о разделяющейся оси. Проецирование векторов обоих рёбер на вектор, перпендикулярный первичному лучу, даст результаты с разными знаками, если одно из рёбер блокирует другое. Также в зависимости от знака проекции первого ребра мы можем узнать, какой из двух вспомогательных лучей необходим. На Рис. 6 сверху показаны три возможные ситуации, а внизу — результаты проецирования. Чёрная точка обозначает позицию наблюдателя, из которой испускается первичный луч (красный). Векторы рёбер (чёрные) проецируются на перпендикулярный первичному вектор (зелёный). Если вспомогательные лучи не требуются, обе проекции дают отрицательные значения, потому что оба вектора рёбер находятся в отрицательном полупространстве перпендикуляра. В двух других случаях, где нужны вспомогательные лучи (оранжевые), знаки проекций отличаются от знаков векторов; если знак отрицателен для вектора более длинного ребра, то достаточно повёрнутого по часовой стрелке вспомогательного луча, а если он положителен, достаточно луча, повёрнутого против часовой стрелки.

3 Блокирующие рёбра и угловые точки

В рассматриваемой нами задаче видимость ограничена углом и расстоянием; это приводит нас к интересным ситуациям.

• Угловыми точками становятся не все концы рёбер, а только находящиеся в области сектора видимости.
  
  • Это как минимум вдвое снижает количество испускаемых лучей. n теперь становится ещё меньше.
  • Чтобы воспользоваться этим преимуществом, следует приложить усилия для отделения угловых точек от концов рёбер. Используемая для этого техника должна быть достаточно быстрой, чтобы само отделение не занимало слишком много времени.
  
  
• Кроме того, большинство рёбер потенциально не будут блокирующими; для нас важны только те, которые содержатся в секторе или отсекаются им.
  
  • Это позволяет снизить количество необходимых проверок пересечений. Значение m должно снизиться.
  • Для этой цели нам также следует придумать быстрый алгоритм отсечения ненужных рёбер.

Основное отличие или отклонение от базового алгоритма, объяснённого в разделе 2, заключается в том, что могут существовать угловые точки, не входящие в множество концов рёбер. Может потребоваться определение большего количества угловых точек. См. конфигурации на Рис. 7 и 8. Концы рёбер находятся за пределами сектора видимости, поэтому бесполезны в качестве угловых точек. Все угловые точки, необходимые для правильного определения области видимости (отмеченные чёрным, синим и красным) не совпадают с концами рёбер. Необходима каждая из них, невозможность испускания луча в любую из них приведёт к неправильному определению области видимости. В чём они отличаются и как их определить?

Поскольку зрение ограничено углом видимости, две угловые точки необходимы и должны безусловно приниматься вне зависимости от наличия ребра. Они являются крайними точками на рёбрах сектора. В них испускаются лучи и определяются точки попадания. На Рис. 7 чёрным показана одна из этих подразумеваемых угловых точек: угловая точка, возникшая из-за точки правого ребра сектора. Испущенный в неё луч заблокирован ребром, что привело к появлению синей точки. Другой луч, испущенный в угловую точку левого ребра, проходит беспрепятственно. Поэтому точкой попадания становится сама угловая точка, выделенная синим. Итак, синие точки определять просто, они не требуют проверок. Их положение постоянно и зависит от положения и направления сектора видимости.

Рассмотрим красную угловую точку (превратившуюся в точку попадания, потому что луч ничем не заблокирован) в пересечении дуги и ребра сектора. Она требует ещё одной проверки пересечения: проверки пересечения дуги и отрезка прямой. Эти угловые точки необходимы, когда ребро пересекает дугу сектора.


Рис. 7

Луч показан остриём стрелки, а ребро имеет конечные точки.


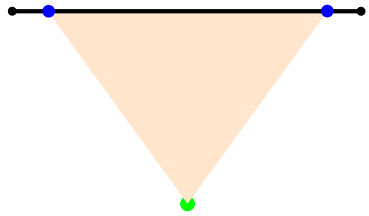
Рис. 8

С учётом этого мы перечислим случаи возникновения угловых точек:

• Любая конечная точка ребра, находящаяся в секторе видимости
• Любая точка дуги сектора, в которой её пересекает ребро

Кроме того, потенциально блокирующими рёбрами являются рёбра, полностью или частично находящиеся в секторе.

Теперь проблема становится задачей получения множества угловых точек (поиска новых и отбрасывания ненужных конечных точек) и множества потенциально блокирующих рёбер (отсечение неблокирующих рёбер). Эту задачу необходимо выполнять быстро, как можно раньше отбрасывая неправильные элементы, чтобы не обременять циклы обработки результатами, которые потом будут отброшены. Цель заключается в снижении значений n (количество испущенных лучей = количество угловых точек) и m (количество отрезков для проверки пересечения с лучом = количество потенциально блокирующих рёбер), обеспечивающем быстрый алгоритм для определения FoV.

3.1 Отсечение

В [3] предполагается, что идеальный алгоритм отсечения (в реальности он будет ресурсоёмким и осложнённым проблемами точности чисел с плавающей запятой) оставляет только множество видимых точек, а достаточно хороший алгоритм отбрасывает большинство невидимых, оставляя точно видимые и потенциально видимые. Он будет консервативен при отбрасывании потенциально видимых точек. Другими словами, если он не может быть совершенно уверен, что ребро не мешает видимости, он не будет отбрасывать его.

3.1.1 Этап раннего, тривиального отбрасывания

Простейшая идея для отбрасывания неподходящих конечных точек и рёбер — проверять только конечные точки рёбер, находящиеся внутри сектора. Это подходит для угловых точек, но недостаточно для блокирующих рёбер, потому что не сработает в конфигурациях, где конечные точки рёбер не находятся в секторе, но ребро блокирует видимость (см. Рис. 7 и 8). Прежде чем переходить к более детальному анализу, проверку конечных точек, если мы можем отбросить ребро, можно полностью пропустить.

3.1.1.1 Пересечение ребра с ограничивающей окружностью

Если ближайшая к центру окружности точка отрезка находится внутри окружности, то он либо находится в нём, либо пересекает его. Этот подход подробно описан в [4]. С помощью ребра и ограничивающей окружности сектора мы можем отбросить все рёбра, не входящие в ограничивающую окружность. После этого этапа все рёбра, не находящиеся в окружности, не рассматриваются. Поскольку это не проверка для поиска точек пересечения, а просто отсечение лишних рёбер, то результат представляется в булевой форме и получается довольно быстро. Для реализации этой проверки нам нужна только пара операций векторного вычитания (дающих вектор) и скалярные произведения: одно для нахождения ближайшей точки (проецированием), а другое для расчёта квадрата расстояния от неё до центра окружности.

Результаты этой проверки показаны на Рис. 9. Ограничивающая окружность сектора видимости отмечена пунктиром. Синяя точка на каждом ребре обозначает ближайшую к центру окружности точку. Зелёные рёбра сохраняются для дальнейших расчётов. Сиреневые тоже сохраняются, но являются ложноположительными. Красные отбрасываются. Ребро, касающееся ограничивающей окружности, тоже отбрасывается, потому что не препятствует видимости.


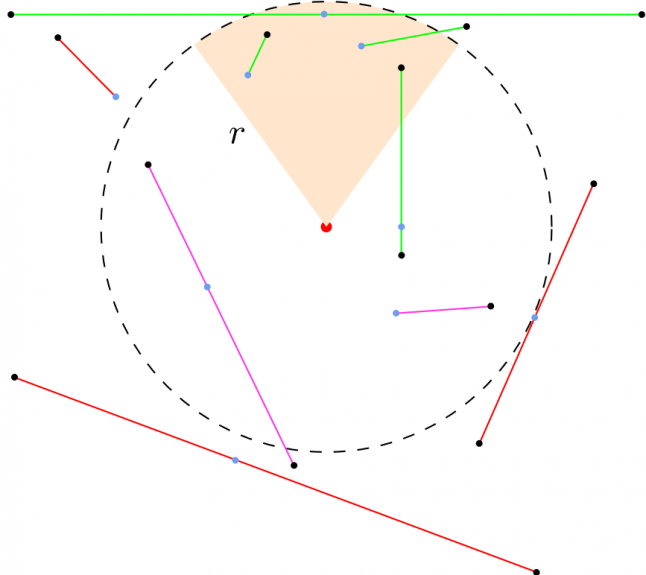
Рис. 9

Для агрессивного отбрасывания ложноположительных результатов привлекательной выглядит идея проверки ближайшей точки в секторе, а не в окружности. Однако, такая проверка некорректна, ведь она будет отбрасывать положительные результаты. На Рис. 9 вместе с сиреневыми точками будет также отброшено зелёное ребро, ближайшая точка которого находится за пределами сектора.

3.1.1.2 Точка относительно сектора

Имея точку и сектор, можно быстро определить

1. находится ли точка за наблюдателем
2. перед наблюдателем и
   
   1. за пределами расстояния видимости
   2. в пределах расстояния видимости и
      
      1. внутри сектора
      2. за пределами сектора, но внутри ограничивающей полуокружности

с помощью только скалярных и векторных произведений. Поскольку векторное произведение не определено в 2D, мы переносим векторы в 3D, принимая z = 0. Результаты векторного произведения являются вектором, но так как z = 0, элементы, относящиеся к x и y будут равны 0, и ненулевой будет только величина z (если векторы непараллельны). Таким образом мы получим из этого векторного произведения скалярный результат. См. различные определения векторного произведения в 2D в [5].

Пусть вектор из центра окружности к точке будет (U), а векторы рёбер сектора — E1, E2. У нас уже есть направление взгляда V.

1. Если U ⋅ V < 0, то точка находится за наблюдателем.
2. иначе если U ⋅ U = ‖U‖² > r², то точка находится за пределами видимости.
3. иначе если sign(E1 × U) = sign(U × E2), то точка находится в секторе.
4. иначе она в окружающей полуокружности, но за пределами сектора.

Мы использовали две оптимизации, требующие объяснений. Мы сравниваем квадраты длин (2) вместо сравнения длин, потому что нахождение длины означает использование sqrt (квадратного корня). Мы избегаем этого и применяем оптимизацию, привычную для работы с компьютерной графикой ([7]). Для проверки того, находится ли точка внутри сектора (3), мы можем найти угол, противолежащий первому ребру сектора и проверить, находится ли он внутри допустимого угла видимости (2θ). Однако для этого нужно воспользоваться тригонометрической функцией acos (арккосинус), что может быть затратнее, чем расчёт пары векторных произведений, в котором используются только арифметические операции.

Если ребро «пережило» предыдущую проверку, мы проверяем его конечные точки, чтобы определить, где они расположены. На Рис. 10 показана текущая ситуация: серые точки за наблюдателем (1), красные — за пределами сектора (2), зелёные конечные точки — внутри сектора (3), а сиреневая находится внутри ограничивающей полуокружности, но за пределами сектора (4).


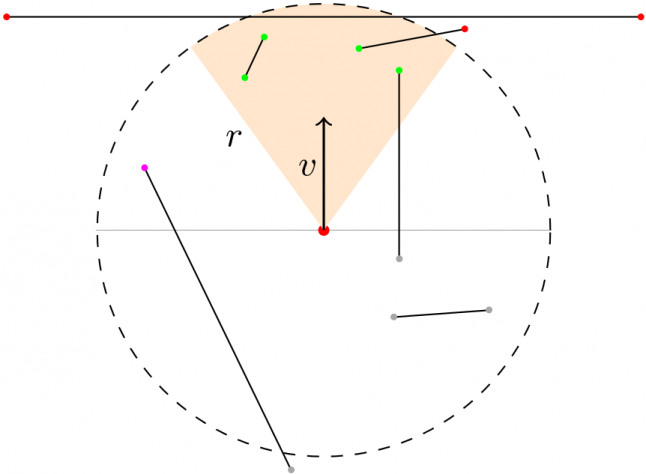
Рис. 10

Угловые точки и блокирующие рёбра можно определить из результатов:

1. Если оба конца за наблюдателем (1), они не мешают видимости; отбрасываем их и больше не обрабатываем.
2. Если оба конца внутри сектора (3), помечаем оба как угловые точки, а ребро — как блокирующее. Прекращаем дальнейшую обработку.
3. Если одна из них внутри сектора (3), а другая нет — (1), (2), (4) — помечаем одну внутри как угловую точку, а ребро — как блокирующее. Это ребро может пересекать дугу сектора и создать новую угловую точку.
4. Если обе за пределами сектора — (2), (4) — конечные точки не являются угловыми, но ребро может пересекать дугу сектора, создавая новые угловые точки. Ребро может быть блокирующим, если пересекает дугу или рёбра сектора.

В случаях 3 и 4 нам требуются дополнительные проверки для нахождения угловых точек, не являющихся конечными точками, содержащихся внутри рёбер и блокировки видимости рёбрами. Это приводит нас к этапу сужения отсечения.

3.2 Этап сужения

На этом этапе мы избавляемся от других ложноположительных результатов с помощью более затратных проверок, чтобы повысить производительность при испускании лучей. Мы можем провести проверки пересечения ребра и дуги арки и/или ребра и ребра.

Однако перед выполнением немного затратной проверки пересечения отрезка и дуги (в ней используется квадратный корень и больше трёх операций ветвления) мы можем использовать результаты предыдущей проверки, чтобы убедиться в необходимости проверки. Проверка нужна только когда ребро имеет возможность пересечь дугу. Если обе конечные точки находятся внутри ограничивающей окружности, ребро не сможет пересечь окружность. Ребро может пересечь дугу сектора только если одна из его конечных точек находится перед наблюдателем, а другая — за пределами ограничивающей окружности (случай 2.1 в разделе 3.1.1.2).

Таблица 1. Возможные положения и состояния конечных точек рёбер

№	Конец А	Конец Б	Состояние
1	Внутри	Внутри (2.2.1)	Угловые точки: A, Б • блокирует
2	Внутри	Сзади (1)	Угловая точка: A • блокирует
3	Внутри	В полуокружности (2.2.2)	Угловая точка: A • блокирует
4	Внутри	За пределами (2.1)	Угловая точка: A • блокирует • может пересекать дугу
5	Сзади	Сзади	Отбрасывается
6	Сзади	За пределами	Может пересекать дугу • может блокировать
7	Сзади	В полуокружности	Может блокировать
8	В полуокружности	В полуокружности	Может блокировать
9	В полуокружности	За пределами	Может пересекать дугу • может блокировать
10	За пределами	За пределами	Может пересекать дугу • может блокировать

С пунктами 1, 2, 3 и 5 мы уже имели дело на этапе раннего отбрасывания и с ними ничего уже делать не нужно. Для пункта 4 требуется проверка пересечения ребра с дугой, чтобы убедиться, что не нужна дополнительная угловая точка. На раннем этапе мы уже пометили одну из его конечных точек как угловую точку, а ребро — как блокирующее. Пункты 6-10 — самые интересные на этапе сужения. Для пунктов 6, 9 и 10 нужна проверка пересечения ребра с дугой, чтобы знать, возникают ли угловые точки при пересечении. Если это так, то ребро должно быть помечено как блокирующее. Если эти пункты не проходят проверку, они присоединяются к пунктам 7 и 8. Они не могут иметь угловых точек, но всё равно должны пройти проверку пересечения ребра и ребра, чтобы знать, блокируют ли они видимость.

3.2.1 Пересечение ребра и дуги сектора

Для пунктов 4, 6, 9 и 10 Таблицы 1 мы с помощью проверки пересечения отрезка и дуги проверяем, пересекает ли ребро дугу сектора [6]. Если это так, то помечаем точки пересечения как угловые точки, а ребро — как блокирующее. Дальнейшая обработка не требуется. Если это не так, ребро не может иметь угловых точек, но ребро должно пройти следующую проверку на блокировку видимости.

В сущности, это проверка пересечения линии и окружности, результатом которой являются две точки. Точки, лежащие и на отрезке, и на дуге, считаются точками пересечения. Здесь можно внести небольшую оптимизацию: если обе точки пересечения находятся за наблюдателем, то отрезок не может блокировать видимость и иметь угловые точки, поэтому ребро можно отбросить без дальнейшей обработки.


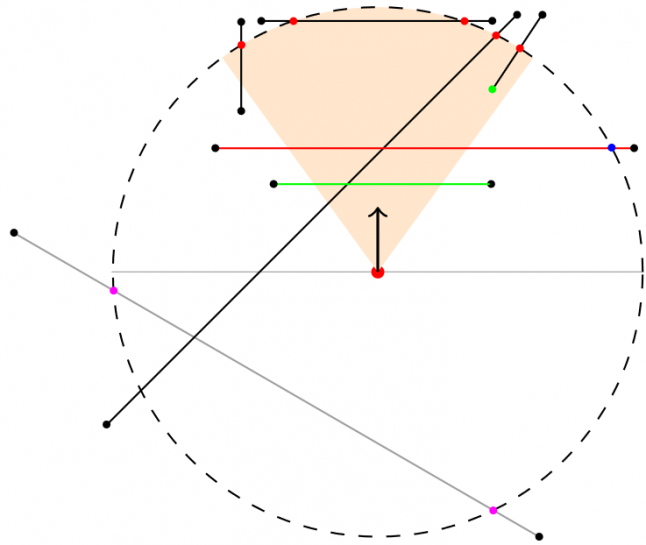
Рис. 11

На Рис. 11 проверяется серое ребро с одной конечной точкой за пределами видимости, а другой конечной точкой — за наблюдателем, но обе точки пересечения сзади наблюдателя (сиреневые), а поэтому отбрасываются. Зелёное ребро с обеими точками в полуокружности никогда не проверяется. Красное ребро с одной конечной точкой за пределами видимости проверяется, но единственная найденная точка пересечения (синяя) не находится на дуге. Это ребро не может иметь угловых точек, но отправляется на следующий этап (проверка пересечения ребра и ребра) для проверки на блокировку. Все другие рёбра (чёрные) с одной или обеими конечными точками за пределами ограничивающей окружности, имеющие подходящие (красные) точки пересечения помечаются как блокирующие, а точки пересечения — как угловые точки Каждое такое ребро соответствует одному из пунктов 4, 6, 9 или 10 в Таблице 1.

3.2.2 Пересечение ребра и ребра сектора

Для пунктов 7 и 8, которые ни разу не проходили предыдущую проверку и для пунктов (6, 9 и 10), проходивших проверку, не обнаружившую точек пересечения, на ребре не может быть угловых точек. Обе его конечные точки не находятся внутри сектора, и на дуге не лежат новые угловые точки. Однако такие рёбра нельзя отбрасывать, потому что они всё равно могут блокировать (см. Рис. 8) или не блокировать (см. Рис. 10; ребро с сиреневой конечной точкой). У нас есть два варианта: подстраховаться и пометить их как блокирующие или для уверенности проверить их на пересечение с рёбрами сектора. Выбрав первый вариант, для каждого ложноположительного непересечения с сектором видимости мы платим проверками пересечения отрезка и отрезка n на этапе испускания лучей, потому что каждый луч проверяется на пересечение с каждой потенциально блокирующим ребром. Вместо того, чтобы расплачиваться n раз за ложноположительные результаты, лучшим вариантом будет потратить n + 2 (в худшем случае). Поэтому мы проверяем ребро на пересечение с обоими рёбрами сектора. Если ребро пересекает хотя бы одно из них, мы помечаем его как блокирующее.


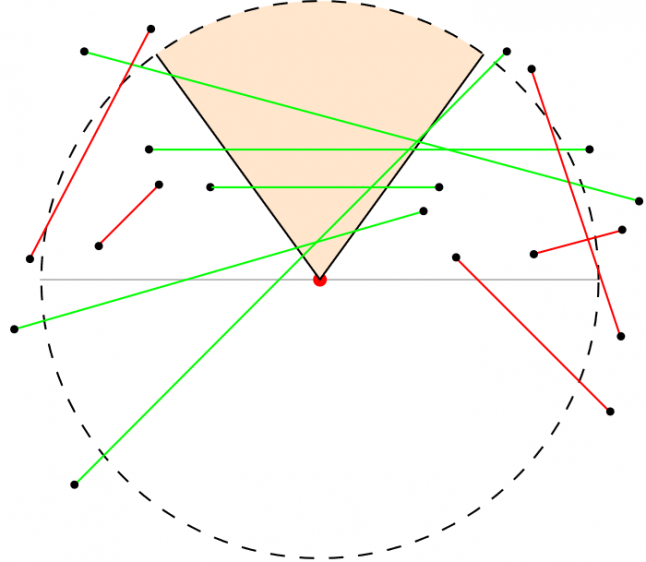
Рис. 12

Для пунктов 6-10 на Рис. 12 есть два соответствующих ребра: одно положительное (зелёное), другое отрицательное (красное). Из рисунка очевидно, что эта проверка имеет большую вероятность отбрасывания рёбер, несоответствующих видимости.

4 Испускание лучей

У нас есть все угловые точки и блокирующие рёбра. Перед выполнением отслеживания лучей необходимо отсортировать угловые точки по углу, чтобы окончательная форма области видимости была правильной при соединении точек попадания рёбрами и дугами. Кроме того, если две или более угловые точки и положение наблюдателя коллинеарны, то в одном направлении будет испущено несколько лучей. Необходимо отбросить дублирующие угловые точки, чтобы избежать лишних лучей.

Для сортировки может использоваться техника. описанная в разделе 3.1.1.2: использование векторного произведения для определения того, находится ли точка внутри сектора видимости. Дублирующие угловые точки можно с лёгкостью снова обработать с помощью векторного произведения. Перед испусканием луча для каждой угловой точки он векторно умножается с предыдущим, и если результат равен нулю, то векторы линейно зависимы (параллельны), а значит, их можно игнорировать.

Первичные лучи испускаются в отсортированные угловые точки. Если мы знаем, что точка является конечной точкой ребра, а не точкой пересечения, то необходимо испустить ещё и вспомогательные лучи (подробнее см. в разделе 2.2). Вспомогательные лучи испускаются только в угловые точки, являющиеся конечными точками рёбер, и не испускаются в точки пересечения, потому что те не могут быть углами полигонов, т.е. видимость не может распространяться дальше них.

Для каждого испускаемого луча мы находим точку пересечения луча и ближайшего к нему ребра. Она становится точкой попадания луча. Если эта точка находится за пределами расстояния видимости r, то мы берём точку попадания в качестве точки вдоль луча, которая находится на расстоянии r от наблюдателя. Т.е. мы перетаскиваем точку попадания назад, пока расстояние от неё до наблюдателя не становится равным r. Мы проверяем, находится ли каждая найденная точка попадания на границе дуги. Если эта и предыдущая точка находится на границе дуги, то мы соединяем их дугой, а в противном случае — отрезком. Однако при выполнении этой задачи «вслепую» возникает небольшая проблема.


Рис. 13

На Рис. 13 точки попадания (пронумерованные справа налево) 1 и 2 находятся на дуге, и должны быть соединены дугой. То же самое в случае с точками попадания 3 и 4. Однако точки попадания 2 и 3 должны быть соединены отрезком, потому что есть ребро, пересекающее дугу. При обнаружении точки попадания 3 и подтверждении того, что она и предыдущая точка попадания находятся на дуге, перед соединением их дугой нужно проверить, параллельна ли соединяющая их линия ближайшему ребру, на котором лежит точка попадания 3. Соединить их отрезком, если они параллельны.

5 Линия взгляда

Запрос линии взгляда необходим для ответа на вопрос, видима ли определённая точка мира X для наблюдателя при заданных параметрах наблюдателя (см. раздел 1). После нахождения блокирующих рёбер и угловых точек сделать это просто. Сначала мы классифицируем X согласно разделу 3.1.1.2. Если точка не внутри сектора, мы возвращаем false. Если она внутри, мы проверяем, пересекает ли какое-нибудь из блокирующих рёбер отрезок, образованный соединением X с наблюдателем. Если он не пересекает, мы возвращаем true, потому что линии взгляда или лучу от наблюдателя к объекту ничего не препятствует. Соответственно, объект видим.

6 Справочные материалы

1. 2D Visibility, Amit Patel
2. Sight & Light, Nicky Case
3. §14.2 Culling Techniques, Real-Time Rendering, Third Editio, Thomas Akenine-Möller, Eric Haines and Naty Hoffman
4. Line segment to circle collision/intersection detection, David Stygstra
5. §A.2.1, 3-D Computer Graphics, Samuel R. Buss
6. Intersection of Linear and Circular Components in 2D, David Eberly
7. §2.2.5, Essential Mathematics for Games and Interactive Applications, Second Edition, James Van Verth and Lars M. Bishop
8. 3D Math Primer for Graphics and Game Development, Second Edition, Fletcher Dunn and Ian Parberry
9. Mathematics for 3D Game Programming and Computer Graphics, Third Edition, Eric Lengyel