 Хей, привет. 2017 год на дворе. Даже простенькие мобильные и браузерные приложения начинают потихоньку рисовать физически корректное освещение. Интернет пестрит кучей статей и готовых шейдеров. И кажется, что это должно быть так просто тоже обмазаться PBR… Или нет?
Хей, привет. 2017 год на дворе. Даже простенькие мобильные и браузерные приложения начинают потихоньку рисовать физически корректное освещение. Интернет пестрит кучей статей и готовых шейдеров. И кажется, что это должно быть так просто тоже обмазаться PBR… Или нет?В действительности же честный PBR сделать достаточно сложно, потому что легко достичь похожего результата, но сложно правильного. И в интернете полно статей, которые делают именно похожий результат, вместо правильного. Отделить мух от котлет в этом хаосе становится сложно.
Поэтому цель статьи не только разобраться, что же такое PBR и как он работает, но и научиться писать его. Как отлаживать, куда смотреть, и какие ошибки типично можно допустить.
Статья рассчитана на людей, которые в достаточной мере уже знают hlsl и неплохо знакомы с линейной алгеброй, и можете написать свой простейший неPBR Phong свет. В общем я постараюсь как можно проще объяснить, но рассчитываю на то, что некоторый опыт работы с шейдерами вы уже имеете.
Примеры будут написаны на Delphi (и собираются под FreePascal), но основной код будет все же на hlsl. Поэтому не стоит пугаться, если вы не знаете Delphi.
Где что можно посмотреть и пощупать?
Для сборки примеров вам понадобится код AvalancheProject. Это мой фреймворк вокруг DX11/OpenGL. Еще понадобится Vampyre Imaging Library. Это библиотека для работы с картинками, я её использую, чтобы загружать текстуры. Сам исходный код примеров находится тут. Для тех, кто не хочет/не может собирать бинарники, а хочет воспользоваться уже собранными, то они тут.
Итак пристегнули ремни, поехали.
1 Важность поддержки sRGB
Наши мониторы обычно показывают sRGB изображение. Это на 95% справедливо для десктопов, и в некоторой степени справедливо для ноутбуков (а на телефонах там сплошной произвол).
Связано это с тем, что наше восприятие не линейно, и небольшие изменения света в темных областях мы замечаем лучше, чем такие же абсолютные изменения в светлых областях. Если грубо — то при повышении яркости в 4 раза мы воспринимаем это как повышение яркости в 2 раза. Я приготовил вам картинку:

Прежде чем пытаться понять картинку — убедитесь, что ваш браузер или операционная система не изменили размеры изображения.
Посредине квадрат, состоящий из горизонтальных однопиксельных черных и белых полос. Количество света от этого квадрата ровно в 2 раза меньше, чем от чисто белого. Теперь если вы отойдете от экрана подальше, чтобы полосы слились в квадрат одного цвета, то на откалиброванном мониторе центральный квадрат должен слиться с правым квадратом, а левый будет значительно темнее. Если вы теперь возьмете пипеткой цвет левого квадрата, то обнаружите что он 128, а правого — 187. Получается, что при смешивании 50/50 черного: 0 0 0 и белого 255 255 255 мы получаем не ~128 128 128, а аж 187 187 187.
Поэтому для физически корректного рендера нам важно, чтобы белый, умноженный на 0.5 на экране превратился в 187 187 187. Для этого в графических API (DirectX и OpenGL) есть аппаратная поддержка sRGB. В момент работы с текстурами в шейдере они переводятся в линейное пространство, а при выводе на экран переводятся обратно в sRGB.
Я не буду подробнее останавливаться на том, как этого добиться в DirectX/OpenGL. Это легко гуглится. А убедится, что ваш sRGB заработал достаточно просто. Линейный градиент от черного к белому должен измениться примерно вот так:

Мне лишь нужно было показать важность работы в линейном пространстве, потому что это одна из первых ошибок, которая встречается в интернете в статьях про PBR.
2 Cook-Torrance
Физически корректный рендер обычно учитывает такие вещи как:
- Коэффициенты отражения Френеля
- Закон сохранения энергии
- Теорию микрограней (microfacet theory) для отраженного света и переизлученного
Список может расширяться на microfacet theory для подповерхностного рассеивания (subsurface scattering) и физически корректного преломления и т.д., но в контексте этой статьи мы поговорим о первых трех пунктах.
2.1 Microfacet Theory
Поверхности различных материалов в реальном мире не абсолютно гладкие, а очень даже шероховатые. Эти микронеровности значительно больше длинны световой волны, и вносят существенный вклад в освещение. Невозможно описать шероховатую плоскость одним вектором нормали, и нормаль обычно описывает некоторое усредненное значение макроповерхности:
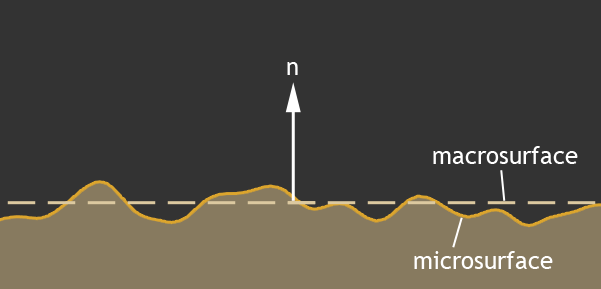
Когда в действительности основной вклад в отраженный свет дают именно микрограни:
Все мы помним, что угол падения равен углу отражения, и вектор h на данном рисунке описывает именно нормаль микрограни, которая дает вклад в освещение. Именно свет от этой точки поверхности мы увидим.
Кроме того, часть света физически не долетит до микрограней, которые могли бы отразить его:

Это называется самозатенение, или self shadowing.
А свет, долетевший до поверхности, и отразившийся — не всегда сможет вылететь:

Это называется самоперекрытие, или masking. А самый хитрый свет сможет отразиться два и больше раз:
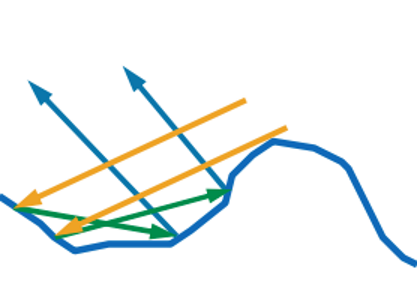
И называется этот эффект — retroreflection. Все эти микрограни описываются коэффициентом шероховатости (roughness), который обычно (но не всегда) лежит в диапазоне (0;1]. При 0 у нас поверхность идеально гладкая, и микрограней нет. При 1 микрограни распределены так, что равновероятно отражают свет по полусфере. Иногда коэффициент шероховатости заменяют коэффициентом гладкости, который равен 1-roughness.
Вот в принципе и все, как ведут себя поверхности для отраженного света.
2.2 Bidirectional Reflectance Distribution Function
Итак, свет попадая на поверхность частично отражается, и частично проникает внутрь материала. Поэтому из общего потока света сначала вычленяют количество отраженного света. Более того, нас интересует не только количество отраженного света, но и количество света, попадающего нам в глаз. И это описывают различные Bidirectional Reflectance Distribution Function (BRDF).
Мы рассмотрим одну из наиболее популярных моделей — модель Cook-Torrance:

В этой функции:
V — вектор от поверхности в глаз наблюдателя
N — макро-нормаль поверхности
L — направление от поверхности к источнику света
D — функция распределения отраженного света с учетом микрограней. Описывает количество микрограней, повернутых к нам так, чтобы отражать свет к нам в глаз.
G — функция распределения самозатенения и самоперекрытия. К сожалению свет, переотраженный несколько раз в этой функции не учитывается, и будет потерян. Мы еще вернемся к этому моменту позже в статье.
F — коэффициенты отражения Френеля. Не весь свет отражается. Часть света преломляется и попадет внутрь материала. В данной функции F описывает количество отраженного света.
Еще в формуле не видно такого параметра, как H вектор, но он активно будет использоваться в D и G функциях распределения. Смысл H вектора — описать нормаль микрограней, которые дают вклад в отраженный свет. Т.е. луч света попавший на микрогрань с нормалью H всегда отразится нам в глаз. Поскольку угол падения равен углу отражения, то мы всегда можем вычислить H, как normalize(V+L). Вот как-то так:
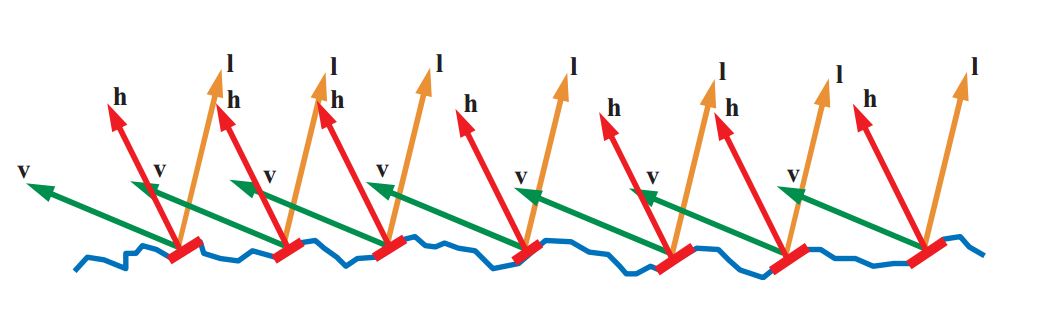
Функции распределения D и G представляют собой приближенное решение, и их много, и разных. Я в конце статьи оставлю ссылочку на список таких распределений. Мы же будем использовать GGX функции распределения, разработанные Bruce Walter-ом.
2.3 G. Геометрия перекрытия
Начнем с самозатенения и перекрытия. Это функция G. GGX распределение этой функции использует метод Smith-а (Smith 1967, «Geometrical shadowing of a random rough surface»). Главный пойнт этого метода заключается в том, что количество потерянного света от света до поверхности и от поверхности до наблюдателя будет симметрично относительно макронормали поврехности. Поэтому функцию G мы можем разбить на 2 части, и посчитать первую половину потерянного света от угла между N и L, а потом используя эту же функцию посчитать потерянный свет от угла между V и N. Вот одну половину такой функции G и описывает распределение GGX:
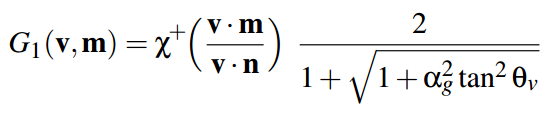
В этой функции
αg — квадрат шероховатости поверхности (roughness*roughness).
θv — угол между макронормалью N и в одном случае светом L, в другом случае вектором на наблюдателя V.
Χ — функция, возвращающая ноль если проверяемый луч приходит с противоположной стороны нормали, в остальных случаях возвращает единицу. В шейдере HLSL мы выкинем это из формулы, т.к. будем проверять на самых ранних этапах, и не освещать такой пиксель вообще. В исходной формуле у нас тангенс, однако для рендера удобно использовать косинус угла, т.к. мы его получаем через скалярное произведение. Поэтому я чуть преобразовал формулу, и записал её в HLSL коде:
float GGX_PartialGeometry(float cosThetaN, float alpha) {
float cosTheta_sqr = saturate(cosThetaN*cosThetaN);
float tan2 = ( 1 - cosTheta_sqr ) / cosTheta_sqr;
float GP = 2 / ( 1 + sqrt( 1 + alpha * alpha * tan2 ) );
return GP;
}И общий G от вектора света и вектора наблюдателя мы считаем так:
float roug_sqr = roughness*roughness;
float G = GGX_PartialGeometry(dot(N,V), roug_sqr) * GGX_PartialGeometry(dot(N,L), roug_sqr);
Если мы отрендерим шарики, и выведем этот G, то получим примерно такую картину:

Источник света находится слева. Шероховатость шариков слева направо от 0.05 до 1.0.
Проверка: Ни один пиксель не должен быть больше единицы. Поставьте вот такое условие:
Out.Color = G;
if (Out.Color.r > 1.000001) Out.Color.gb = 0.0;
Если хоть один аутпут пиксель окажется больше единицы — то он окрасится в красный цвет. Если все сделали правильно — все пиксели останутся белыми.
2.4 D. Распределение отражающих микрограней
Итак у нас есть такие параметры: макронормаль, шерохватость, и H вектор. Из этих параметров можно установить какой % микрограней на данном пикселе имеют нормаль, совпадающую с H. В GGX за это отвечает вот эта функция:
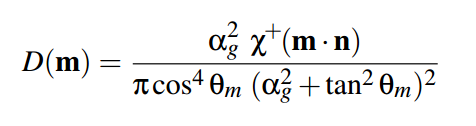
Χ — такая же функция как и в случае с G. Мы её выкидываем по тем же причинам.
αg — квадрат шероховатости поверхности
θm — угол между макронормалью N и нашим H вектором.
Я опять сделал небольшие преобразования, и заменил тангенс на косинус угла. В итоге мы имеем вот такую HLSL функцию:
float GGX_Distribution(float cosThetaNH, float alpha) {
float alpha2 = alpha * alpha;
float NH_sqr = saturate(cosThetaNH * cosThetaNH);
float den = NH_sqr * alpha2 + (1.0 - NH_sqr);
return alpha2 / ( PI * den * den );
}И вызываем её вот так:
float D = GGX_Distribution(dot(N,H), roughness*roughness);Если вывести значение D на экран, то получим примерно такую картину:

Шероховатость по прежнему изменяется от 0.05 слева, до 1.0 справа.
Проверка: Обратите внимание на то, что при шероховатости равной 1.0 весь свет должен распределиться равномерно по полусфере. Это значит что последний шарик обязательно должен быть однотонным. Его цвет должен быть 153 153 153 (+-1 из-за округлений), что при переводе из sRGB в линейное пространство даст 0.318546778125092. Умножив это число на PI мы должны получить примерно единицу, что соответствует отражению по полусфере. Почему PI? Потому что интеграл cos(x)sin(x) по полусфере дает PI.
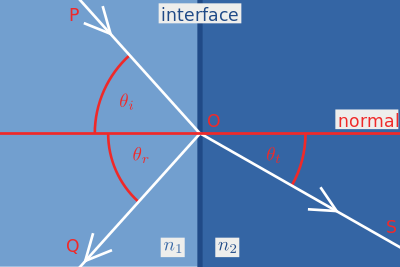
2.5 F. Коэффициенты отражения Френеля
Луч света, попав на границу двух разных сред отражается и преломляется.
Формулы Френеля достаточно точно описывают законы, по которым это происходит, но если вы сходите в вики, и посмотрите на эти многоэтажные формулы, то увидите, что они тяжелые. К счастью есть неплохая аппроксимация, которая используется в большинстве случаев в PBR рендерах, это аппроксимация Шлика:

Где R0 вычисляется как отношение коэффициентов преломления:
а cosθ в формуле — косинус угла между падением света и нормалью. Видно, что при cosθ = 1 формула вырождается в R0, а это значит, что физический смысл R0 — количество отраженного света, если луч падает перпендикулярно поверхности. Давайте сразу оформим это в hlsl код:
float3 FresnelSchlick(float3 F0, float cosTheta) {
return F0 + (1.0 - F0) * pow(1.0 - saturate(cosTheta), 5.0);
}Обратите внимание, что F0 имеет тип float3. Это связано с тем, что коэффициенты отражения могут быть разными для разных каналов. Разные материалы отражают разное количество света в зависимости от длинны волны:
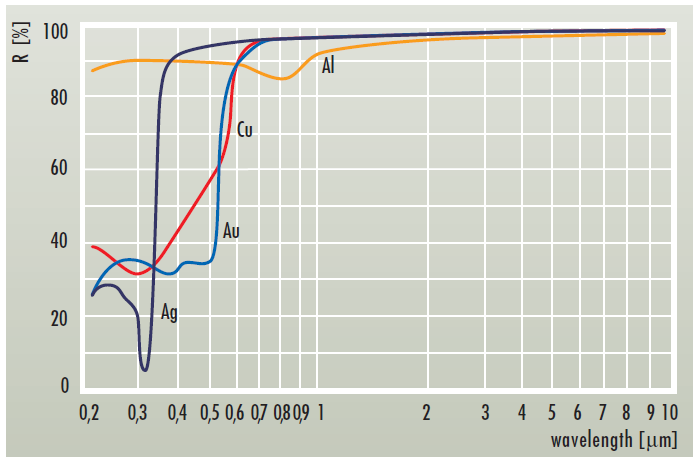
А так как у нас в глазах RGB колбочки, то для людей будет достаточно float3.
2.6 Складываем вместе
Что ж. Давайте теперь соберем нашу функцию, возвращающую отраженный цвет целиком:
float3 CookTorrance_GGX(float3 n, float3 l, float3 v, Material_pbr m) {
n = normalize(n);
v = normalize(v);
l = normalize(l);
float3 h = normalize(v+l);
//precompute dots
float NL = dot(n, l);
if (NL <= 0.0) return 0.0;
float NV = dot(n, v);
if (NV <= 0.0) return 0.0;
float NH = dot(n, h);
float HV = dot(h, v);
//precompute roughness square
float roug_sqr = m.roughness*m.roughness;
//calc coefficients
float G = GGX_PartialGeometry(NV, roug_sqr) * GGX_PartialGeometry(NL, roug_sqr);
float D = GGX_Distribution(NH, roug_sqr);
float3 F = FresnelSchlick(m.f0, HV);
//mix
float3 specK = G*D*F*0.25/NV;
return max(0.0, specK);
}В самом начале мы фильтруем свет, не попавший на поверхность:
if (NL <= 0.0) return 0.0;if (NV <= 0.0) return 0.0;
Обратите внимание, что я не поделил на NL:
float3 specK = G*D*F*0.25/NV;потому, что потом мы все равно умножаем на NL, и NL сокращается. На выходе у меня вышла вот такая картина:
Слева направо шероховатость увеличивается от 0.05 до 1.0
Сверху вниз разные коэффециенты френеля F0:
1. (0.04, 0.04, 0.04)
2. (0.24, 0.24, 0.24)
3. (1.0, 0.86, 0.56)
2.7 Lambertian модель рассеянного света
Итак функция FresnelSchlick вернет нам количество отраженного света. Остальной свет будет равен 1.0-FresnelSchlick().
Здесь я хочу сделать отступление.
Вот эту единицу минус френель многие считают по разному. Например в UE4 FresnelSchlick считают от dot(V,H). Где-то берут два коэффициента (от dot(L,N) и dot(V,N)). Как по мне — логичнее брать от dot(L,N). Сейчас я могу сказать, что я не знаю точно, как правильнее, и как будет ближе к реальности. Когда я изучу этот вопрос, я дополню этот пробел в статье, а пока мы будем делать так, как в UE4, то есть dot(V,H).
Этот свет пройдет сквозь поверхность и будет хаотически блуждать внутри неё, пока не будет поглощен/переизлучен/покинет поверхность в другой точке. Поскольку мы пока не затрагиваем subsurface scattering, то грубо предположим, что этот свет будет поглощен, либо переизлучен по полусфере:

В первом приближении нас это устроит. Описывается данное рассеивание моделью освещения Ламберта. Описывается это простейшей формулой LightColor*dot(N,L)/PI. То есть всем знакомый dot(N,L), который описывает плотность светового потока, попадающего на поверхность, и деление на PI с которым мы уже встречались ранее в виде интеграла полусфере. Количество поглощенного/переизлученного света описывает float3 параметр, который называют albedo. Тут все очень похоже с F0 параметром. Предмет переизлучает только определенные длины волн.
Поскольку больше по модели освещения Ламберт сказать нечего — то мы в наш CookTorrance_GGX добавляем его (хотя возможно правильнее было вынести в отдельную функцию, но мне лень пока вытаскивать F параметр):
float3 specK = G*D*F*0.25/(NV+0.001);
float3 diffK = saturate(1.0-F);
return max(0.0, m.albedo*diffK*NL/PI + specK);
А в целом функция стала вот такой
float3 CookTorrance_GGX(float3 n, float3 l, float3 v, Material_pbr m) {
n = normalize(n);
v = normalize(v);
l = normalize(l);
float3 h = normalize(v+l);
//precompute dots
float NL = dot(n, l);
if (NL <= 0.0) return 0.0;
float NV = dot(n, v);
if (NV <= 0.0) return 0.0;
float NH = dot(n, h);
float HV = dot(h, v);
//precompute roughness square
float roug_sqr = m.roughness*m.roughness;
//calc coefficients
float G = GGX_PartialGeometry(NV, roug_sqr) * GGX_PartialGeometry(NL, roug_sqr);
float D = GGX_Distribution(NH, roug_sqr);
float3 F = FresnelSchlick(m.f0, HV);
//mix
float3 specK = G*D*F*0.25/(NV+0.001);
float3 diffK = saturate(1.0-F);
return max(0.0, m.albedo*diffK*NL/PI + specK);
}Вот что у меня получилось после добавления диффузной составляющей:

Альбедо трех материалов (в линейном пространстве) сверху вниз:
1. (0.47, 0.78, 0.73)
2. (0.86, 0.176, 0)
3. (0.01, 0.01, 0.01)
Ну и вот я поставил второй источник света справа, и увеличил интенсивность источников в 3 раза:

Текущий пример можно скачать вот тут в репозитории. Так же напоминаю, что собранные версии примеров вот тут.
3.0 Image based lighting

Мы сейчас рассмотрели то, как точечный источник света вносит вклад в освещение каждого пикселя изображения. Конечно мы пренебрегли тем, что источник должен затухать от квадрата расстояния, а также тем, что источник не может быть точечным, и можно было бы все это учесть, но давайте посмотрим на еще один подход к освещению. Дело в том, что все предметы вокруг отражают/переизлучают свет, и этим самым освещают окружение. Вы подходите к зеркалу, и видите себя. Отраженный свет в зеркале был не так давно переизлучен/отражен вашим телом, и именно поэтому в видите в нем себя. Если мы хотим в гладких объектах получать красивые отражения, то нам нужно будет для каждого пикселя посчитать свет от полусферы, окружающей этот пиксель. В играх используют в этом случае такой фейк. Подготавливают большую текстуру с окружением (фактически 360° фото либо кубическая карта). Каждый пиксель такой фотографии — маленький эммитер. Дальше с помощью «некоторой магии» выбирают пиксели с таких текстур, и освещают рисующейся пиксель с помощью кода, который мы написали выше для точечных источников. Именно поэтому техника и называется Image based lighting (т.е. текстура окружения используется как источник света).
3.1 Monte-Carlo
Начнем с простого. Воспользуемся методом Монте-Карло, чтобы посчитать наше освещение. Для тех, кто боится и не понимает страшных слов «метод Монте-Карло» попробую объяснить на пальцах. На освещение каждой точки у нас влияют все точки из карты. Половину из них мы можем отсеять. Это те, которые находятся с противоположной стороны поверхности, так как они дадут нулевой вклад в освещение. У нас остается полусфера. Теперь мы можем пускать случайные равномерно распределенные лучи по этой полусфере, и складывать освещение в кучу, а потом поделить на количество пущенных лучей и умножить на 2π. На 2π — это площадь полусферы с радиусом 1. Математики же скажут, что мы проинтегрировали освещение по полусфере методом Монте-Карло.
Как это будет работать на практике? Складывать в кучу мы будем с помощью рендера во floating point текстуру через аддитивный блендинг. В альфаканал этой текстуры мы будем записывать количество наших лучей, а в rgb собственно освещение. Это позволит нам разделить потом color.rgb на color.a и получить финальное изображение.
Однако аддитивный блендинг означает, что объекты, перекрываемые другими объектами у нас начнут просвечивать сквозь другие, так как будут рисоваться. Чтобы избежать этой проблемы мы воспользуемся depth prepass техникой. Суть техники в том, что мы сначала рисуем объекты только в буфер глубины, а потом переключаем тест глубины в equal и рисуем объекты теперь уже в буфер цвета.
Итак, далее я генерирую кучу лучей, равномерно распределенных по сфере:
function RandomRay(): TVec3;
var theta, cosphi, sinphi: Single;
begin
theta := 2 * Pi * Random;
cosphi := 1 - 2 * Random;
sinphi := sqrt(1 - min(1.0, sqr(cosphi)));
Result.x := sinphi * cos(theta);
Result.y := sinphi * sin(theta);
Result.z := cosphi;
end;
SetLength(Result, ACount);
for i := 0 to ACount - 1 do
Result[i] := Vec(RandomRay(), 1.0);и отправляю это добро как константу вот в этот шейдер:
float3 m_albedo;
float3 m_f0;
float m_roughness;
static const float LightInt = 1.0;
#define SamplesCount 1024
#define MaxSamplesCount 1024
float4 uLightDirections[MaxSamplesCount];
TextureCube uEnviroment; SamplerState uEnviromentSampler;
PS_Output PS(VS_Output In) {
PS_Output Out;
Material_pbr m;
m.albedo = m_albedo;
m.f0 = m_f0;
m.roughness = m_roughness;
float3 MacroNormal = normalize(In.vNorm);
float3 ViewDir = normalize(-In.vCoord);
Out.Color.rgb = 0.0;
[fastopt]
for (uint i=0; i<SamplesCount; i++){ //складываем освещение всех лучей в кучу
float3 LightDir = dot(uLightDirections[i].xyz, In.vNorm) < 0 ? -uLightDirections[i].xyz : uLightDirections[i].xyz; //нас интересует только полусфера поэтому переворачиваем луч на 180, если он нам не подходит
float3 LightColor = uEnviroment.SampleLevel(uEnviromentSampler, mul(LightDir, (float3x3)V_InverseMatrix), 0.0).rgb*LightInt; //по лучу берем семпл из кубической карты (наше окружение)
Out.Color.rgb += CookTorrance_GGX(MacroNormal, LightDir, ViewDir, m)*LightColor; //и считаем освещение по уже написанной функции для точечного источника
}
Out.Color.rgb *= 2*PI; //не забываем умножить на площадь единичной полусферы
Out.Color.a = SamplesCount; //и складываем количество лучей в альфаканал
return Out;
}Запускаем, и видим как наша картинка для тех же шариков постепенно сходится. Я использовал две кубические карты для рендера. Вот для этого:

я взял кубическую карту, которая шла вместе с RenderMonkey. Называется она Snow.dds. Это LDR текстура, и она скууучная. Шарики скорее кажутся грязными, чем красиво освещенными.
А для вот этого:

я взял HDR Probe вот отсюда: www.pauldebevec.com/Probes которая называется Grace Cathedral, San Francisco. У неё динамический диапазон аж 200,000:1. Видите какая разница? Поэтому когда будете делать у себя такое освещение — берите сразу HDR текстуру.
Кстати, давайте посмотрим, что закон сохранения энергии выполняется. Для этого я альбедо в шейдере форсированно задаю в 1.0:
m.albedo = 1.0;
свет задаю в 1.0:
LightColor = 1.0;
В идеале каждый пиксель шарика теперь должен стать равен единице. Поэтому все, что выходит за пределы единицы мы пометим красным. У меня вышло вот так:

Фактически то красное, что сейчас есть — это погрешности. Оно начинает сходится, но в какой то момент точности флоата не хватает, и сходимость исчезает. Обратите внимание на то, что правый нижний шарик «посинел». Это из-за того, что модель Ламберта не учитывает шероховатости поверхности, а модель Кука-Торенса учитывает их не полностью. Фактически мы потеряли желтый цвет, который идет в F0. Давайте попробуем F0 всем шарам выставить в 1.0 и посмотрим:

Правые шары стали значительно темнее из-за большого roughness. Фактически это ретрорефлекшн, который мы потеряли. Кук-Торренс просто теряет эту энергию. Частично восстановить эту энергию может модель Орен-Наяра. Но мы пока отложим это. Придется смирится с тем, что для сильно шероховатых моделей мы потеряем до 70% энергии ретроотражений.
Исходный код находится тут. Собранные бинарники я уже упоминал ранее, они находятся тут.
3.2 Importance sampling
Конечно же геймер не будет ждать, когда свет на вашей картинке сойдется. Нужно что-то делать, чтобы не считать тысячи и тысячи лучей для каждого пикселя. И фокус тут вот в чем. Для монтекарло мы считали равномерное распределение по полусфере. Вот так мы делали выборки:

но реальный вклад дает именно часть, обведенная розовым. Если бы мы могли выбирать лучи, преимущественно из красной зоны, мы бы гораздо раньше получили приемлемую картинку. Итак нам хочется вот такого:

К счастью для этого есть математический метод, который называется Importance Sampling (или выборка по значимости). Значимость в нашем выражении вносит параметр D. По нему мы можем построить CDF (функцию распределения), из некоторой PDF функции (функция плотности вероятности). За PDF мы берем распределение микронормали к нашей нормали, сумма по полусфере будет давать единицу, значит мы можем записать такой интеграл:

Здесь подынтегральное выражение — PDF
Взяв интеграл по сферическим углам мы получим вот такую CDF:
Для тех, кто хочет step by step пройти этот этап — можете заглянуть вот сюда.
Для тех, кто не хочет/не может углубляться скажу. У нас есть CDF, в которую мы подставляем равномерно распределенные ξ, на выходе мы получаем распределение, которое отражает нашу PDF. Что это значит для нас?
1. То, что это изменит нашу функцию Кука-Торренса. Её надо будет разделить на PDF функцию.
2. PDF функция отражает распределение микронормали относительно макронормали. Раньше для Монте-Карло мы брали случайный вектор, и принимали его как вектор на источник света. Сейчас с помощью CDF мы выбираем случайный вектор H. Далее отражаем вектор взгляда относительно этого случайного H и получаем вектор света.
3. PDF нашу надо перевести в пространство вида (т.к. она отражает распределение вдоль вектора N). Для перевода нам нужно нашу PDF разделить на 4*dot(H,V) Кому интересно вникнуть глубже — идем сюда и там есть объяснения в параграфе 4.1 и дальше с рисунками на кружочках.
Кажется, что ничего непонятно, да? Давайте попробуем переварить все это в коде.
Для начала напишем функцию, генерирующую вектор H из нашей CDF. В HLSL это будет вот так:
float3 GGX_Sample(float2 E, float alpha) {
float Phi = 2.0*PI*E.x;
float cosThetha = saturate(sqrt( (1.0 - E.y) / (1.0 + alpha*alpha * E.y - E.y) ));
float sinThetha = sqrt( 1.0 - cosThetha*cosThetha);
return float3(sinThetha*cos(Phi), sinThetha*sin(Phi), cosThetha);
}Сюда в E мы подаем равномерное распределение [0;1) для обоих сферических углов, в alpha у нас квадрат от roughness материала.
На выходе получаем H вектор на полусфере. Но эту полусферу нужно ориентировать по поверхности. Для этого пишем еще одну функцию, которая будет возвращать нам матрицу ориентации на поверхности:
float3x3 GetSampleTransform(float3 Normal) {
float3x3 w;
float3 up = abs(Normal.y) < 0.999 ? float3(0,1,0) : float3(1,0,0);
w[0] = normalize ( cross( up, Normal ) );
w[1] = cross( Normal, w[0] );
w[2] = Normal;
return w;
}На эту матрицу мы будем умножать все наши сгенерированные вектора H, переводя их касательного пространство в пространство вида. Принцип очень похож на TBN базис.
Теперь осталось поделить нашего Кука-Торренса: G*D*F*0.25/(NV) на PDF. Наша PDF = D*NH/(4*HV). Поэтому наш измененный Кук-Торренс получается:
G*F*HV/(NV*NH)
В HLSL теперь это выглядит вот так:
float3 CookTorrance_GGX_sample(float3 n, float3 l, float3 v, Material_pbr m, out float3 FK) {
pdf = 0.0;
FK = 0.0;
n = normalize(n);
v = normalize(v);
l = normalize(l);
float3 h = normalize(v+l);
//precompute dots
float NL = dot(n, l);
if (NL <= 0.0) return 0.0;
float NV = dot(n, v);
if (NV <= 0.0) return 0.0;
float NH = dot(n, h);
float HV = dot(h, v);
//precompute roughness square
float roug_sqr = m.roughness*m.roughness;
//calc coefficients
float G = GGX_PartialGeometry(NV, roug_sqr) * GGX_PartialGeometry(NL, roug_sqr);
float3 F = FresnelSchlick(m.f0, HV);
FK = F;
float3 specK = G*F*HV/(NV*NH);
return max(0.0, specK);
}Обратите внимание, что я выкинул из этой функции диффузную часть от Ламбертовского освещения, и возвращаю наружу FK параметр. Дело в том, что мы не можем диффузную составляющую считать через Importance Sampling, т.к. наша PDF — она для граней, отражающих свет нам в глаз. А распределение Ламберта не зависит от этого. Что же делать? Хм… а давайте пока диффузную часть оставим черной, и сосредоточимся на спекуляре.
PS_Output PS(VS_Output In) {
PS_Output Out;
Material_pbr m;
m.albedo = m_albedo;
m.f0 = m_f0;
m.roughness = m_roughness;
float3 MacroNormal = normalize(In.vNorm);
float3 ViewDir = normalize(-In.vCoord);
float3x3 HTransform = GetSampleTransform(MacroNormal);
Out.Color.rgb = 0.0;
float3 specColor = 0.0;
float3 FK_summ = 0.0;
for (uint i=0; i<(uint)uSamplesCount; i++){
float3 H = GGX_Sample(uHammersleyPts[i].xy, m.roughness*m.roughness); //генерим H вектор
H = mul(H, HTransform); //переводим из пространства модели в пространство вида
float3 LightDir = reflect(-ViewDir, H); //отражаем вектор взгляда чтобы получить вектор света
float3 specK;
float3 FK;
specK = CookTorrance_GGX_sample(MacroNormal, LightDir, ViewDir, m, FK); //считаем количество спекуляра
FK_summ += FK;
float3 LightColor = uRadiance.SampleLevel(uRadianceSampler, mul(LightDir.xyz, (float3x3)V_InverseMatrix), 0).rgb*LightInt;//и множим его на пиксель из карты света
specColor += specK * LightColor; //добавляем в сумму
}
specColor /= uSamplesCount;
FK_summ /= uSamplesCount;
Out.Color.rgb = specColor;
Out.Color.a = 1.0;
return Out;
}Зададим 1024 семпла (без аккумулирования как в монте-карло) и посмотрим на результат:
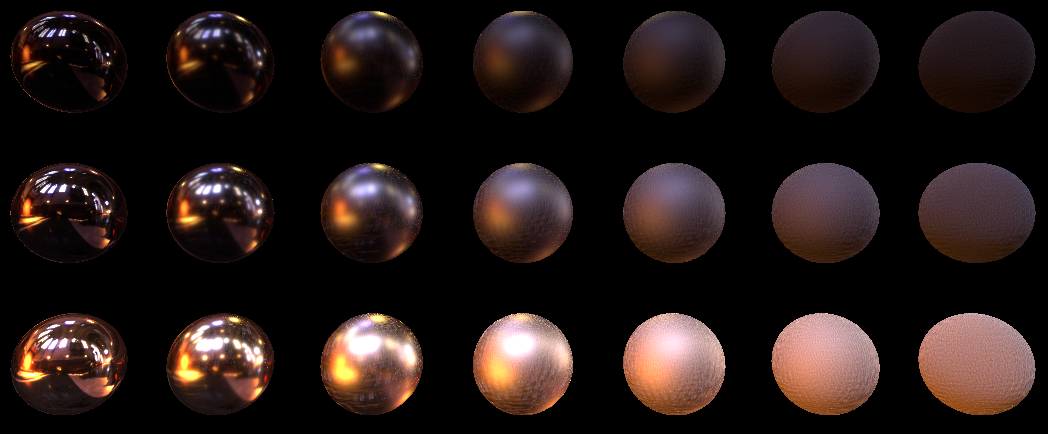
Хоть семплов и много, а вышло шумновато. Особенно на большом roughness.
3.3 Выбор LOD-ов
Это потому, что мы семплы берем с высокодетализированной карты, с нулевого LOD. А хорошо бы для лучей, имеющих большое отклонение брать лод поменьше. Ситуацию хорошо иллюстрирует вот эта картинка:

Из этой статьи от NVidia. Синие области показывают усреденное значение, которое неплохо бы взять из LOD-ов текстуры. Видно что для более значимых мы берем LOD поменьше, а для менее значимых побольше, т.е. берем усредненное по области значение. Идеально было бы, если бы мы лодами покрыли целиком полусферу. К счастью NVidia уже дала нам готовую (и простую по их словам) формулу:

Эта формула состоит из разности:

Левая часть у нас зависит от размеров текстуры и количества семплов. А это значит что для всех семплов мы её можем посчитать один раз. В правой части у нас функция p, которая ничто иное как наша pdf, и функция d, которую они называют distortion, но по сути там зависимость от угла семпла к наблюдателю. Для d у них выходит вот такая формула:

Заголовок спойлера
(Внимание, данная формула справедлива для Dual-Paraboloid карт. У нас используется кубическая карта, и я полагаю, что коэффициент b для нашего случая может быть другой, но я это еще не проверял. В моем случае коэффициент предложенный в статье b=1.2 сработал достаточно неплохо)
Ну и еще NVidia рекомендуют делать bias для лодов, добавлять единичку. Давайте посмотрим как это выглядит в hlsl коде. Вот наша левая часть уравнения:
float ComputeLOD_AParam(){
float w, h;
uRadiance.GetDimensions(w, h);
return 0.5*log2(w*h/uSamplesCount);
}Вот мы считаем правую часть, и сразу вычитаем её из левой:
float ComputeLOD(float AParam, float pdf, float3 l) {
float du = 2.0*1.2*(abs(l.z)+1.0);
return max(0.0, AParam-0.5*log2(pdf*du*du)+1.0);
}Теперь мы видим, что нам в ComputeLOD нужно передать pdf и l значения. l — это вектор семпла света, а pdf, если мы посмотрим выше то это у нас: pdf = D*dot(N,H)/(4*dot(H,V)).
Поэтому давайте в нашу функцию CookTorrance_GGX_sample добавим возвращающийся параметр pdf:
float3 CookTorrance_GGX_sample(float3 n, float3 l, float3 v, Material_pbr m, out float3 FK, out float pdf) {
pdf = 0.0;
FK = 0.0;
n = normalize(n);
v = normalize(v);
l = normalize(l);
float3 h = normalize(v+l);
//precompute dots
float NL = dot(n, l);
if (NL <= 0.0) return 0.0;
float NV = dot(n, v);
if (NV <= 0.0) return 0.0;
float NH = dot(n, h);
float HV = dot(h, v);
//precompute roughness square
float roug_sqr = m.roughness*m.roughness;
//calc coefficients
float G = GGX_PartialGeometry(NV, roug_sqr) * GGX_PartialGeometry(NL, roug_sqr);
float3 F = FresnelSchlick(m.f0, HV);
FK = F;
float D = GGX_Distribution(NH, roug_sqr); //вот тут собственно мы добавили вычисление D
pdf = D*NH/(4.0*HV); //и вычисление самой pdf
float3 specK = G*F*HV/(NV*NH);
return max(0.0, specK);
}А сам цикл по семплам теперь у нас вычисляет LOD:
float LOD_Aparam = ComputeLOD_AParam();
for (uint i=0; i<(uint)uSamplesCount; i++){
float3 H = GGX_Sample(uHammersleyPts[i].xy, m.roughness*m.roughness);
H = mul(H, HTransform);
float3 LightDir = reflect(-ViewDir, H);
float3 specK;
float pdf;
float3 FK;
specK = CookTorrance_GGX_sample(MacroNormal, LightDir, ViewDir, m, FK, pdf);
FK_summ += FK;
float LOD = ComputeLOD(LOD_Aparam, pdf, LightDir);
float3 LightColor = uRadiance.SampleLevel(uRadianceSampler, mul(LightDir.xyz, (float3x3)V_InverseMatrix), LOD).rgb*LightInt;
specColor += specK * LightColor;
}Давайте же глянем, что у нас получилось для 1024 семплов с лодами:

Выглядит идеально. Понижаем до 16, и…
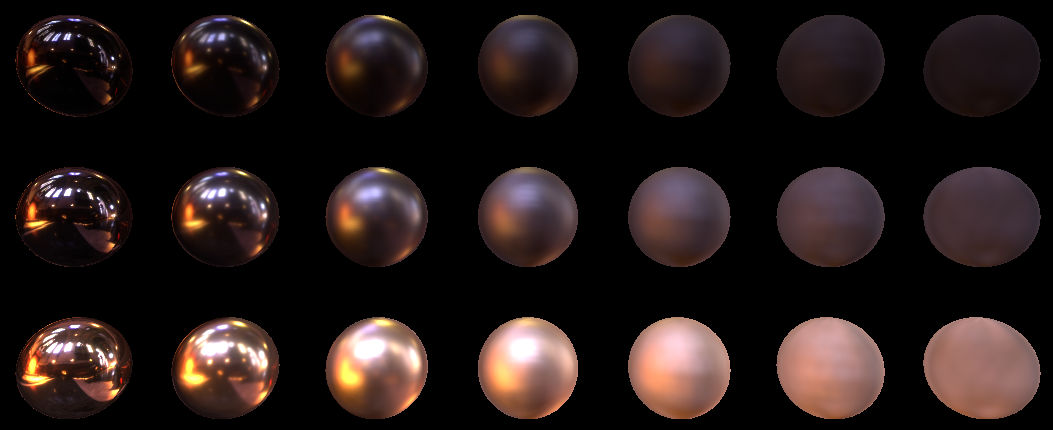
Да, конечно уже не совсем идеально. Видно что качество пострадало на шариках с большим roughness, но тем не менее я считаю это качество в принципе приемлемым. Дополнительно повысить качество можно было бы, если бы мы mip-ы для текстур построили на основе нашего распределения. Об этом можно прочесть в презентации от Epic вот тут (см. параграф Pre-Filtered Environment Map). А пока в рамках этой статьи я предлагаю остановиться на классических пирамидальных мипах.
3.4 Hammersley point set
Если посмотреть на наши случайный лучи, то понятен недостаток. Они случайны. А мы уже научились читать из lod-ов и хотим нашими лучами захватить как можно большую площадь. Для этого нам нужно «распылить» наши лучи, но с учетом importance sampling-а. Т.к. CDF у нас принимает равномерное распределение, то нам достаточно равномерно расположить точки на промежутке [0;1)… но у нас равномерное распределение должно быть двумерным. Поэтому надо не только равномерно расположить точки на промежутке, но еще и сделать так, чтобы расстояние в декартовых координатах между точками было как можно больше. На эту роль хорошо подходят Hammersley point set. Чуть больше про это множество точек можно почитать вот тут.
Я лишь покажу картинку распределения:

А так же приведу функцию, генерирующую отдельную из точек:
function HammersleyPoint(const I, N: Integer): TVec2;
function radicalInverse_VdC(bits: Cardinal): Single;
begin
bits := (bits shl 16) or (bits shr 16);
bits := ((bits and $55555555) shl 1) or ((bits and $AAAAAAAA) shr 1);
bits := ((bits and $33333333) shl 2) or ((bits and $CCCCCCCC) shr 2);
bits := ((bits and $0F0F0F0F) shl 4) or ((bits and $F0F0F0F0) shr 4);
bits := ((bits and $00FF00FF) shl 8) or ((bits and $FF00FF00) shr 8);
Result := bits * 2.3283064365386963e-10;
end;
begin
Result.x := I/N;
Result.y := radicalInverse_VdC(I);
end;Как наши шары будут выглядеть с этим набором точек? На самом деле я схалтурил, и все вышеописанные картинки для Importance Sampling-а сгенерированы именно с набором этих точек. На случайных наборах картинки выглядят чуть хуже (поверите на слово?)
3.5 Irradiance map
Помните как мы остались без диффузного цвета? Мы не можем семплить диффузный цвет с помощью importance sampling, потому что наш importance sampling выбирает наиболее ценные лучи для спекуляра. Для диффуза же наиболее ценные находятся прямо напротив, по макронормали поверхности. К счастью диффузная составляющая для Ламберта у нас совершенно не зависит от наблюдателя. Поэтому мы можем предрасчитать освещение в кубической карте. А еще один бонус — изменение угла настолько незначительно влияет на освещение, что предрасчитанная карта может быть очень низкого разрешения, например 16*16 пикселей на сторону.
На этот раз нам повезло. Мы не будем писать код, который занимается построением Irradiance map, а воспользуемся программой CubeMapGen. Просто открываем нашу кубмапу (Load Cubemap (.dds) ), выставляем галку Irradiance cubemap, выбираем Output Cube Size 16:
и сохраняем получившуюся кубическую карту (для HDR текстур не забываем выставить нужный формат аутпут текстуры).
Ну и поскольку мы разобрались с Irradiance map, то просто после семплинга добавляем одну выборку из этой карты. Наш HLSL код теперь выглядит так:
Out.Color.rgb = 0.0;
float3 specColor = 0.0;
float3 FK_summ = 0.0;
for (uint i=0; i<(uint)uSamplesCount; i++){
float3 H = GGX_Sample(uHammersleyPts[i].xy, m.roughness*m.roughness);
H = mul(H, HTransform);
float3 LightDir = reflect(-ViewDir, H);
float3 specK;
float pdf;
float3 FK;
specK = CookTorrance_GGX_sample(MacroNormal, LightDir, ViewDir, m, FK, pdf);
FK_summ += FK;
float LOD = ComputeLOD(LOD_Aparam, pdf, LightDir);
float3 LightColor = uRadiance.SampleLevel(uRadianceSampler, mul(LightDir.xyz, (float3x3)V_InverseMatrix), LOD).rgb*LightInt;
specColor += specK * LightColor;
}
specColor /= uSamplesCount;
FK_summ /= uSamplesCount;
float3 LightColor = uIrradiance.Sample(uIrradianceSampler, mul(MacroNormal, (float3x3)V_InverseMatrix)).rgb;
Out.Color.rgb = m.albedo*saturate(1.0-FK_summ)*LightColor + specColor;А на выходе имеем вот такую картинку для 16 семплов:

И такую для 1024
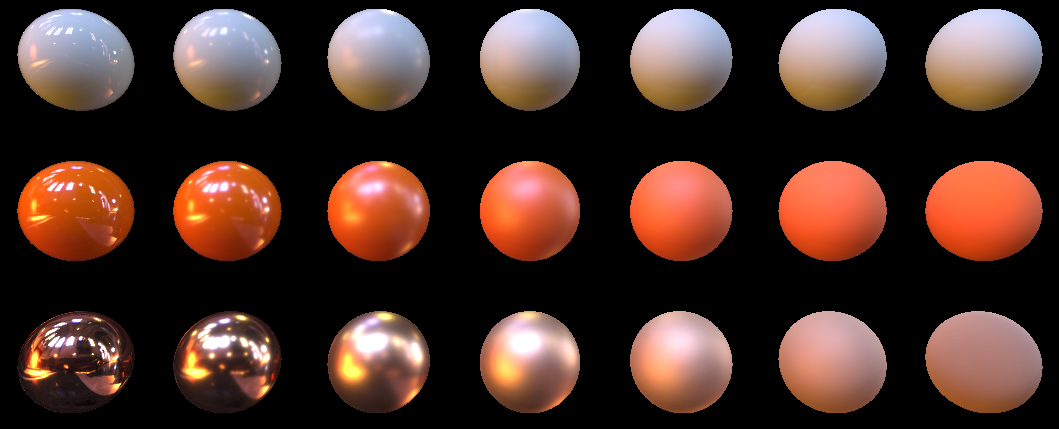
Обратите внимание, что диффузный свет мы уже не умножаем на dot(N,L), что как бы логично. Ведь это освещение мы предрасчитали и запекли в кубмапу, и в нашем случае N и L это вообще один и тот же вектор.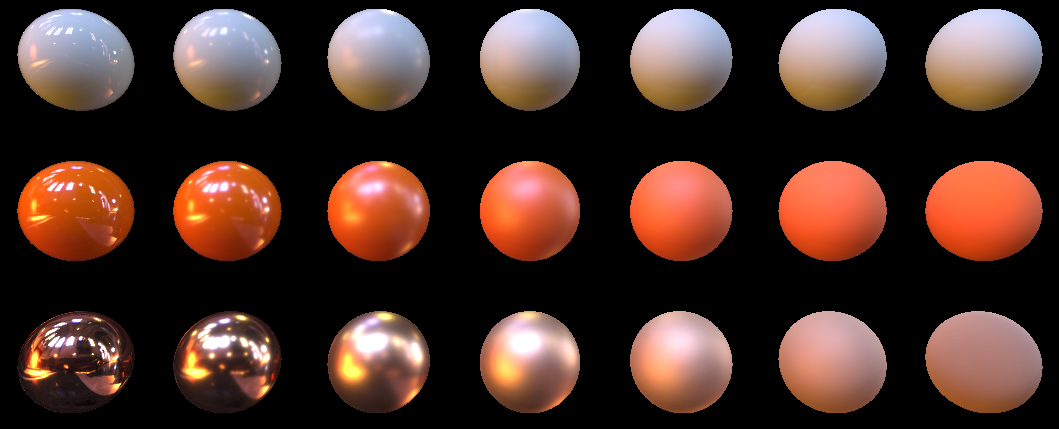
Давайте глянем, что у нас там с сохранением энергии? Как обычно выставляем свет из кубических карт равным единице, альбедо материала выставляем равным единице, и подсвечиваем красным области >1. Получаем примерно это для 1024 семплов:

И вот это для 16:

Как видим есть явные «выбросы» лишней энергии, но они небольшие. Связано это с тем, что мы не точно рассчитываем количество света от диффузной энергии. Ведь мы считаем коэффициенты Френеля только для определенных семплов спекуляра, а используем их для всех семлов, которые предрасчитаны в irradiance map. Увы, я не знаю что с этим делать, интернет ничего мне не смог подсказать. Поэтому предлагаю пока смириться с этим, все таки выбросы лишней энергии не значительны.
4 Еще чуть-чуть про материалы.
Пока мы возились с шариками — вы должно быть заметили, что у нас есть два float3 параметра цвета. Это albedo и f0. Они оба имеют некоторый физический смысл, но в играх как правило материалы разделяют на металлы и неметаллы. Дело в том, что неметаллы отражают свет всегда в grayscale диапазонах, но при этом переизлучают цвентной свет. Металлы же наоборот, отражают цветной свет, но при этом поглощают весь остальной.
То есть для металлов у нас:
albedo = {0, 0, 0}
f0 = {R, G, B}
для диэлектриков у нас:
albedo = {R, G, B}
f0 = {X, X, X}
и… мы видим, что мы можем ввести некоторый коэффициент [0,1], которым мы будем показывать насколько у нас поверхность металлическая, и считать материал просто через линейную интерполяцию. Это собственно многие художники и делают. Я скачал вот эту 3д модель.
Вот например текстуры меча.
Текстура цвета:

Текстура шероховатости:

И наконец текстура металличности (та самая, о которой выше я рассказал):

Чуть больше о материалах вы можете прочитать в интернете. Например тут.
Разные движки и студии могут паковать параметры по разному, но как правило все крутится вокруг: цвета, шероховатости, металличности.
Ну и наконец, как это выглядит на модели целиком:

слева — все тот же собор, который мы тестировали на шариках. Справа наш Арториас выбрался на природу (карта окружения отсюда www.pauldebevec.com/Probes называется Campus)
Для рендера данных изображений я использовал дополнительно Reinhard тонмаппинг, но это тема уже для отдельной статьи.
Исходный код с моделью Арториаса — это демка в моем фреймворке, и находится вот тут. Так же я собрал для вас версию, и выложил тут.
5 Заключение
Статья вышла гораздо больше, чем я предполагал. Я хотел рассказать еще про:
1. Анизотропные модели освещения
2. Подповерхностное рассеивание
3. Продвинутые диффузные модели освещения, типа Орен-Наяра
4. Захватить сферические гармоники
5. Захватить тонмаппинг
Но верите или нет, я выдохся пока писал эту статью… А тут каждый пункт — это жирный пласт. Поэтому есть, что есть. Может быть когда-нибудь я расскажу про все это.
Надеюсь что моя статья приоткроет кому-нибудь завесу тайны, скрытой за этими буквами PBR. И спасибо за внимание.
Полезные материалы по PBR и около того
[1] blog.tobias-franke.eu/2014/03/30/notes_on_importance_sampling.html
откуда взялись PDF и CDF, и как их посчитать самому.
[2] hal.inria.fr/hal-00942452v1/document
хороший математический материал по PBR (+ анизотропные распределения)
[3] disney-animation.s3.amazonaws.com/library/s2012_pbs_disney_brdf_notes_v2.pdf
хороший материал от Disney, что как можно запаковать и предрасчитать. Сравнение погрешностей, а так же пример нескольких диффузных моделей освещения
[4] blog.selfshadow.com/publications/s2015-shading-course/#course_content
И еще более свежий материал от Disney
[5] www.cs.cornell.edu/~srm/publications/EGSR07-btdf.pdf
Подробно о GGX, от Bruce Walter-а и других умных ребят
[6] de45xmedrsdbp.cloudfront.net/Resources/files/2013SiggraphPresentationsNotes-26915738.pdf
Про PBR в Unreal Engine 4
[7] holger.dammertz.org/stuff/notes_HammersleyOnHemisphere.html
Классная инструкция по Hammersley Point Set
[8] www.jordanstevenstechart.com/physically-based-rendering
Различные функции распределения. С картиночками.
[9] graphicrants.blogspot.nl/2013/08/specular-brdf-reference.html
еще функции распределения
[10] developer.nvidia.com/gpugems/GPUGems3/gpugems3_ch20.html
Очень полезный материал от NVidia про Importance Sampling и оптимизацию LOD-ами.
[11] cgg.mff.cuni.cz/~jaroslav/papers/2008-egsr-fis/2008-egsr-fis-final-embedded.pdf
Еще один неплохой пейпер про Importance Sampling
[12] gdcvault.com/play/1024478/PBR-Diffuse-Lighting-for-GGX
Просто очень качественные слайды по PBR.
[13] www.codinglabs.net/article_physically_based_rendering.aspx
[14] www.codinglabs.net/article_physically_based_rendering_cook_torrance.aspx
Две очень хорошие для понимания основ статьи (но содержат кое-какие ошибки и неточности)
[15] www.rorydriscoll.com/2009/01/25/energy-conservation-in-games
Про сохранение энергии
[16] www.gamedev.net/topic/625981-lambert-and-the-division-by-pi
www.wolframalpha.com/input/?i=integrate+cos+x+*+sin+x+dx+dy+from+x+%3D+0+to+pi+%2F+2+y+%3D+0+to+pi+*+2
откуда Пи в знаменателе
[17]https://seblagarde.files.wordpress.com/2015/07/course_notes_moving_frostbite_to_pbr_v32.pdf
[18] www.pauldebevec.com/Probes
Набор HDR 360 проб. Прямо с формулами как читать из этих проб.
[19] seblagarde.wordpress.com/2012/06/10/amd-cubemapgen-for-physically-based-rendering
code.google.com/archive/p/cubemapgen/downloads
КубМапГен. Тулза для обработки radiance и irradiance кубических карт.
[20] eheitzresearch.wordpress.com/415-2
Про полигональные источники света. С демкой.
откуда взялись PDF и CDF, и как их посчитать самому.
[2] hal.inria.fr/hal-00942452v1/document
хороший математический материал по PBR (+ анизотропные распределения)
[3] disney-animation.s3.amazonaws.com/library/s2012_pbs_disney_brdf_notes_v2.pdf
хороший материал от Disney, что как можно запаковать и предрасчитать. Сравнение погрешностей, а так же пример нескольких диффузных моделей освещения
[4] blog.selfshadow.com/publications/s2015-shading-course/#course_content
И еще более свежий материал от Disney
[5] www.cs.cornell.edu/~srm/publications/EGSR07-btdf.pdf
Подробно о GGX, от Bruce Walter-а и других умных ребят
[6] de45xmedrsdbp.cloudfront.net/Resources/files/2013SiggraphPresentationsNotes-26915738.pdf
Про PBR в Unreal Engine 4
[7] holger.dammertz.org/stuff/notes_HammersleyOnHemisphere.html
Классная инструкция по Hammersley Point Set
[8] www.jordanstevenstechart.com/physically-based-rendering
Различные функции распределения. С картиночками.
[9] graphicrants.blogspot.nl/2013/08/specular-brdf-reference.html
еще функции распределения
[10] developer.nvidia.com/gpugems/GPUGems3/gpugems3_ch20.html
Очень полезный материал от NVidia про Importance Sampling и оптимизацию LOD-ами.
[11] cgg.mff.cuni.cz/~jaroslav/papers/2008-egsr-fis/2008-egsr-fis-final-embedded.pdf
Еще один неплохой пейпер про Importance Sampling
[12] gdcvault.com/play/1024478/PBR-Diffuse-Lighting-for-GGX
Просто очень качественные слайды по PBR.
[13] www.codinglabs.net/article_physically_based_rendering.aspx
[14] www.codinglabs.net/article_physically_based_rendering_cook_torrance.aspx
Две очень хорошие для понимания основ статьи (но содержат кое-какие ошибки и неточности)
[15] www.rorydriscoll.com/2009/01/25/energy-conservation-in-games
Про сохранение энергии
[16] www.gamedev.net/topic/625981-lambert-and-the-division-by-pi
www.wolframalpha.com/input/?i=integrate+cos+x+*+sin+x+dx+dy+from+x+%3D+0+to+pi+%2F+2+y+%3D+0+to+pi+*+2
откуда Пи в знаменателе
[17]https://seblagarde.files.wordpress.com/2015/07/course_notes_moving_frostbite_to_pbr_v32.pdf
[18] www.pauldebevec.com/Probes
Набор HDR 360 проб. Прямо с формулами как читать из этих проб.
[19] seblagarde.wordpress.com/2012/06/10/amd-cubemapgen-for-physically-based-rendering
code.google.com/archive/p/cubemapgen/downloads
КубМапГен. Тулза для обработки radiance и irradiance кубических карт.
[20] eheitzresearch.wordpress.com/415-2
Про полигональные источники света. С демкой.
