В коде id Software порой встречаются бесподобные жемчужины. Самая знаменитая — это, конечно, 0x5f3759df, удостоившаяся даже комикса на xkcd. Здесь же речь пойдёт о заливке экрана: пиксели закрашиваются по одному в случайном порядке, без повторов. Как это сделано?

Лобовым решением было бы использовать генератор случайных чисел и перед закраской каждого пикселя проверять, не закрашен ли он до сих пор. Это было бы крайне неэффективно: к тому моменту, когда на экране остаётся последний незакрашенный пиксель, потребуется порядка 320×200 вызовов ГСЧ, чтобы в него «попасть». (Вспомним, что Wolfenstein 3D работал на 286 с частотой 12МГц!) Другим лобовым решением было бы составить список из всех 320×200 возможных координат, перетасовать его (можно даже заранее, и вставить в код уже перетасованным), и закрашивать пиксели по списку; но для этого понадобилось бы как минимум 320×200×2 = 125КБ памяти — пятая часть всей памяти компьютера! (Помните ведь, что 640КБ должно было хватить любому?)
Вот как на самом деле реализована эта попиксельная заливка: (код немного упрощён по сравнению с оригиналом)
Что за чертовщина здесь происходит?
Для тех, кому тяжело разбираться в ассемблерном коде для 8086 — вот эквивалентный код на чистом Си:
Проще говоря:
Эта «магия» называется регистр сдвига с линейной обратной связью: для генерации каждого следующего значения мы выдвигаем один бит вправо, и вдвигаем слева новый бит, который получается как результат xor. Например, четырёхбитный РСЛОС с «отводами» на нулевом и втором битах, xor которых задаёт вдвигаемый слева бит, выглядит так:

Если взять начальное значение 1, то этот РСЛОС генерирует пять других значений, а потом зацикливается: 0001 → 1000 → 0100 → 1010 → 0101 → 0010 → 0001 (подчёркнуты биты, используемые для xor). Если взять начальное значение, не участвующее в этом цикле, то получится другой цикл: например, 0011 → 1001 → 1100 → 1110 → 1111 → 0111 → 0011. Легко проверить, что три четырёхбитных значения, не попавшие ни в один из этих двух циклов, образуют третий цикл. Нулевое значение всегда переходит само в себя, поэтому оно не рассматривается в числе возможных.
А можно ли подобрать отводы РСЛОС так, чтобы все возможные значения образовали один большой цикл? Да, если в поле по модулю 2 разложить на множители многочлен xN+1, где N=2m–1 — длина получающегося цикла. Опуская хардкорную математику, покажем, как четырёхбитный РСЛОС с отводами на нулевом и первом битах будет поочерёдно принимать все 15 возможных значений:
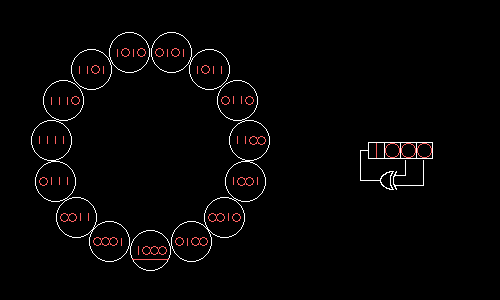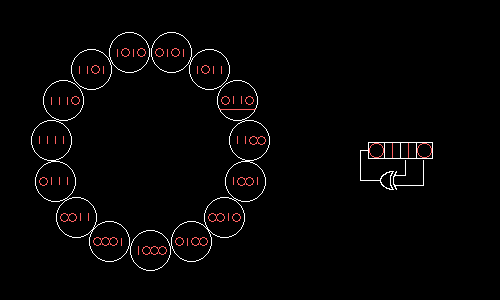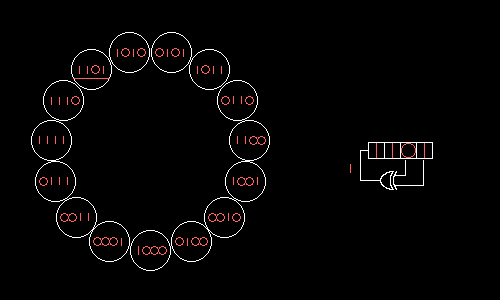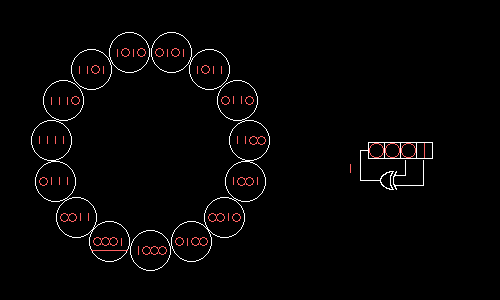
Wolfenstein 3D использует 17-битный РСЛОС с отводами на нулевом и третьем битах. Этот РСЛОС можно было бы реализовать «в лоб» за семь логических операций:
Такая реализация называется «конфигурацией Фибоначчи». Равнозначная ей «конфигурация Галуа» позволяет выполнить всё то же самое за три логические операции:
Если заметить, что старший бит после сдвига гарантированно нулевой, то копирование и xor можно объединить в одну операцию:
Значение в «конфигурации Галуа» по сравнению с «конфигурацией Фибоначчи» циклически сдвинуто на три бита: начальному значению 1 в конфигурации Галуа (используемому в коде Wolfenstein 3D) соответствует начальное значение 8 в конфигурации Фибоначчи. Вторым значением РСЛОС будет 0x12000, соответствующее 0x10004 в конфигурации Фибоначчи, и так далее. Если одна из последовательностей принимает все возможные (ненулевые) значения — значит, и вторая тоже принимает все эти значения, хоть и в другом порядке. Из-за того, что нулевое значение для РСЛОС недостижимо, из значения координаты y в коде вычитается единица — иначе пиксель (0,0) так никогда бы и не закрасился.
В заключение автор оригинальной статьи упоминает, что из 217–1 = 131071 значений, генерируемых этим РСЛОС, используются только 320×200 = 64000, т.е. чуть меньше половины; каждое второе генерируемое значение отбрасывается, т.е. генератор работает в половину доступной скорости. Для нужд Wolfenstein 3D хватило бы и 16-битного РСЛОС, и тогда не пришлось бы заморачиваться с обработкой 32-битного

Лобовым решением было бы использовать генератор случайных чисел и перед закраской каждого пикселя проверять, не закрашен ли он до сих пор. Это было бы крайне неэффективно: к тому моменту, когда на экране остаётся последний незакрашенный пиксель, потребуется порядка 320×200 вызовов ГСЧ, чтобы в него «попасть». (Вспомним, что Wolfenstein 3D работал на 286 с частотой 12МГц!) Другим лобовым решением было бы составить список из всех 320×200 возможных координат, перетасовать его (можно даже заранее, и вставить в код уже перетасованным), и закрашивать пиксели по списку; но для этого понадобилось бы как минимум 320×200×2 = 125КБ памяти — пятая часть всей памяти компьютера! (Помните ведь, что 640КБ должно было хватить любому?)
Вот как на самом деле реализована эта попиксельная заливка: (код немного упрощён по сравнению с оригиналом)
boolean FizzleFade(unsigned width, unsigned height) { unsigned x, y; long rndval = 1; do // while (1) { // seperate random value into x/y pair asm mov ax, [WORD PTR rndval] asm mov dx, [WORD PTR rndval+2] asm mov bx, ax asm dec bl asm mov [BYTE PTR y], bl // low 8 bits - 1 = y xoordinate asm mov bx, ax asm mov cx, dx asm mov [BYTE PTR x], ah // next 9 bits = x xoordinate asm mov [BYTE PTR x+1], dl // advance to next random element asm shr dx, 1 asm rcr ax, 1 asm jnc noxor asm xor dx, 0x0001 asm xor ax, 0x2000 noxor: asm mov [WORD PTR rndval], ax asm mov [WORD PTR rndval+2], dx if (x>width || y>height) continue; // copy one pixel into (x, y) if (rndval == 1) // entire sequence has been completed return false ; } while (1); }
Что за чертовщина здесь происходит?
Для тех, кому тяжело разбираться в ассемблерном коде для 8086 — вот эквивалентный код на чистом Си:
void FizzleFade(unsigned width, unsigned height) { unsigned x, y; long rndval = 1; do { y = (rndval & 0x000FF) - 1; // младшие 8 бит - 1 = координата y x = (rndval & 0x1FF00) >> 8; // следующие 9 bits = координата x unsigned lsb = rndval & 1; // младший бит потеряется при сдвиге rndval >>= 1; if (lsb) // если выдвинутый бит = 0, то не надо xor rndval ^= 0x00012000; if (x<=width && y<=height) copy_pixel_into(x, y); } while (rndval != 1); }
Проще говоря:
rndvalначинается с 1;- каждый раз разделяем значение
rndvalна координаты x и y, и закрашиваем пиксель с этими координатами; - каждый раз сдвигаем и xor-им
rndvalс непонятной «магической константой»; - когда
rndvalкаким-то образом снова примет значение 1 — готово, весь экран залит.
Эта «магия» называется регистр сдвига с линейной обратной связью: для генерации каждого следующего значения мы выдвигаем один бит вправо, и вдвигаем слева новый бит, который получается как результат xor. Например, четырёхбитный РСЛОС с «отводами» на нулевом и втором битах, xor которых задаёт вдвигаемый слева бит, выглядит так:
Если взять начальное значение 1, то этот РСЛОС генерирует пять других значений, а потом зацикливается: 0001 → 1000 → 0100 → 1010 → 0101 → 0010 → 0001 (подчёркнуты биты, используемые для xor). Если взять начальное значение, не участвующее в этом цикле, то получится другой цикл: например, 0011 → 1001 → 1100 → 1110 → 1111 → 0111 → 0011. Легко проверить, что три четырёхбитных значения, не попавшие ни в один из этих двух циклов, образуют третий цикл. Нулевое значение всегда переходит само в себя, поэтому оно не рассматривается в числе возможных.
А можно ли подобрать отводы РСЛОС так, чтобы все возможные значения образовали один большой цикл? Да, если в поле по модулю 2 разложить на множители многочлен xN+1, где N=2m–1 — длина получающегося цикла. Опуская хардкорную математику, покажем, как четырёхбитный РСЛОС с отводами на нулевом и первом битах будет поочерёдно принимать все 15 возможных значений:

Wolfenstein 3D использует 17-битный РСЛОС с отводами на нулевом и третьем битах. Этот РСЛОС можно было бы реализовать «в лоб» за семь логических операций:
unsigned new_bit = (rndval & 1) ^ (rndval>>3 & 1); rndval >>= 1; rndval |= (new_bit << 16);
Такая реализация называется «конфигурацией Фибоначчи». Равнозначная ей «конфигурация Галуа» позволяет выполнить всё то же самое за три логические операции:
a → b → c → d → e → f → g → h → i → j → k → l → m → n → o → p → q ↑ Фибоначчи ↓ ↓ ·← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ←^← ← ← ← ← ←· o → p → q→^→a → b → c → d → e → f → g → h → i → j → k → l → m → n ↑ ↑ Галуа ↓ ·← ← ← ← ←·← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ←·
- сдвигаем значение вправо;
- копируем выдвинутый бит (n) в самую старшую позицию;
- xor-им этот бит с 13-тым (q).
Если заметить, что старший бит после сдвига гарантированно нулевой, то копирование и xor можно объединить в одну операцию:
— что мы и видим в коде Wolfenstein 3D.unsigned lsb = rndval & 1; rndval >>= 1; if (lsb) rndval ^= 0x00012000;
Значение в «конфигурации Галуа» по сравнению с «конфигурацией Фибоначчи» циклически сдвинуто на три бита: начальному значению 1 в конфигурации Галуа (используемому в коде Wolfenstein 3D) соответствует начальное значение 8 в конфигурации Фибоначчи. Вторым значением РСЛОС будет 0x12000, соответствующее 0x10004 в конфигурации Фибоначчи, и так далее. Если одна из последовательностей принимает все возможные (ненулевые) значения — значит, и вторая тоже принимает все эти значения, хоть и в другом порядке. Из-за того, что нулевое значение для РСЛОС недостижимо, из значения координаты y в коде вычитается единица — иначе пиксель (0,0) так никогда бы и не закрасился.
В заключение автор оригинальной статьи упоминает, что из 217–1 = 131071 значений, генерируемых этим РСЛОС, используются только 320×200 = 64000, т.е. чуть меньше половины; каждое второе генерируемое значение отбрасывается, т.е. генератор работает в половину доступной скорости. Для нужд Wolfenstein 3D хватило бы и 16-битного РСЛОС, и тогда не пришлось бы заморачиваться с обработкой 32-битного
rndval на 16-битном процессоре. Автор предполагает, что программисты id Software просто не смогли найти подходящую комбинацию «отводов», которая давала бы максимальный 16-битный цикл. Мне же кажется, что он сильно их недооценивает :-) Дело в том, что для разделения 16-битного значения на координаты x и y его пришлось бы делить с остатком на 320 или на 200, и затраты на такую операцию деления с лихвой бы скомпенсировали всё ускорение от перехода на 16-битный РСЛОС.