Neural Ordinary Differential Equations
Значительная доля процессов описывается дифференциальными уравнениями, это могут быть эволюция физической системы во времени, медицинское состояние пациента, фундаментальные характеристики фондового рынка и т.д. Данные о таких процессах последовательны и непрерывны по своей природе, в том смысле, что наблюдения — это просто проявления какого-то непрерывно изменяющегося состояния.
Есть также и другой тип последовательных данных, это дискретные данные, например, данные NLP задач. Состояния в таких данных меняется дискретно: от одного символа или слова к другому.
Сейчас оба типа таких последовательных данных обычно обрабатываются рекуррентными сетями, несмотря на то, что они отличны по своей природе, и похоже, требуют различных подходов.
На последней NIPS-конференции была представлена одна очень интересная статья, которая может помочь решить эту проблему. Авторы предлагают подход, который они назвали Нейронные Обыкновенные Дифференциальные Уравнения (Neural ODE).
Здесь я постарался воспроизвести и кратко изложить результаты этой статьи, чтобы сделать знакомство с ее идеей чуть более простым. Мне кажется, что эта новая архитектура вполне может найти место в стандартном инструментарии дата-сайентиста наряду со сверточными и рекуррентными сетями.
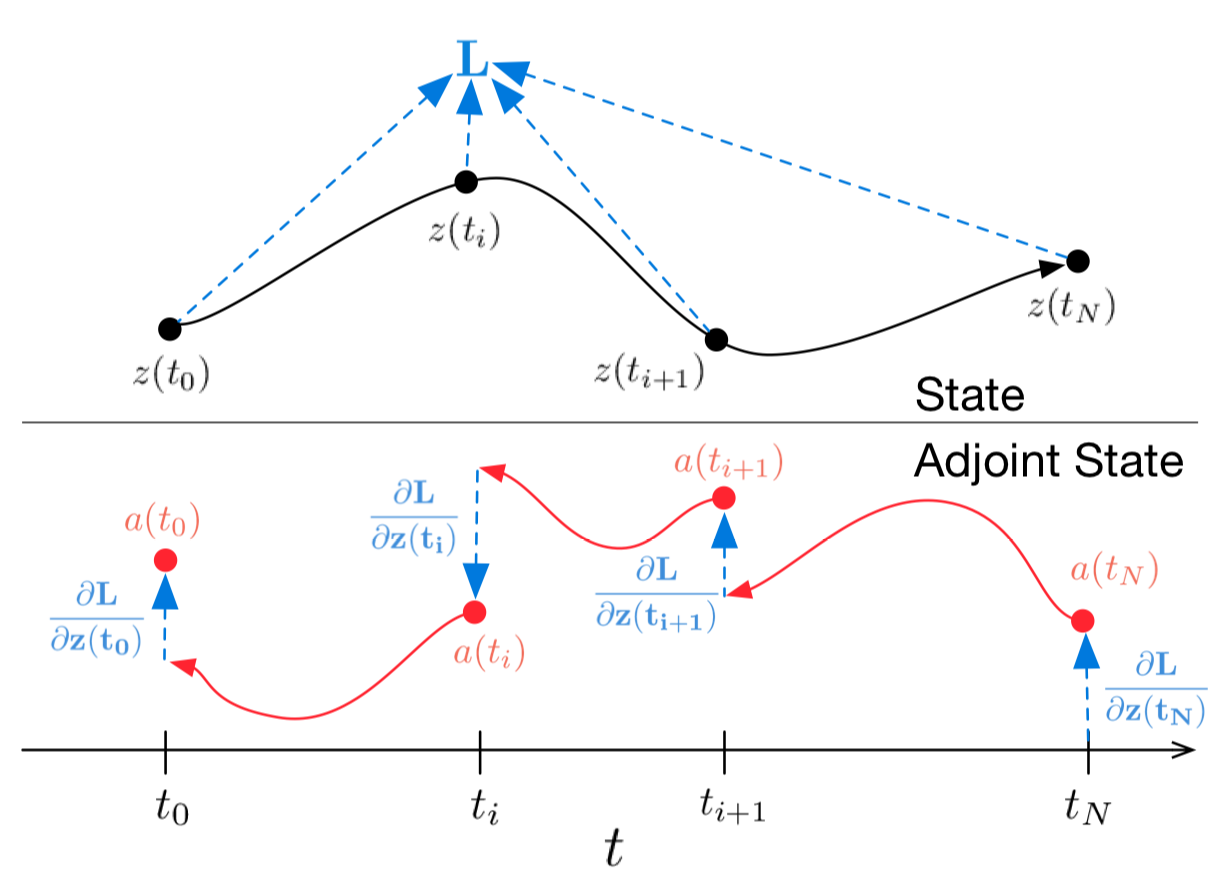
Картинка 1: Непрерывный backpropagation градиента требует решения аугментированного дифференциального уравнения назад во времени.
Стрелки представляют корректировку распространенных назад градиентов градиентами от наблюдений.
Иллюстрация из оригинальной статьи
Постановка проблемы
Пусть есть процесс, который подчиняется некоторому неизвестному ОДУ и пусть есть несколько (зашумленных) наблюдений вдоль траектории процесса
Как найти аппроксимацию
Сначала рассмотрим более простую задачу: есть только 2 наблюдения, в начале и в конце траектории,
Эволюция системы запускается из состояния
Или, более формально, рассмотрим минимизацию функции потерь
Чтобы минимизировать
Вывод этой формулы можно посмотреть в аппендиксе оригинальной статьи.
Векторы в этой статье следует считать строчными векторами, хотя оригинальная статья использует и строчное и столбцовое представление.
Решая диффур (4) назад во времени, получаем зависимость от начального состояния
Чтобы рассчитать градиент по отношению к
Тогда сопряженное состояние к этому аугментированному состоянию:
Градиент аугментированной динамики:
Дифференциальное уравнение сопряженного аугментированного состояния из формулы (4) тогда:
Решение этого ОДУ назад во времени дает:
Что вместе с
дает градиенты по всем входным параметрам в решатель ОДУ ODESolve.
Все градиенты (10), (11), (12), (13) могут быть рассчитаны вместе за один вызов ODESolve с динамикой сопряженного аугментированного состояния (9).

Иллюстрация из оригинальной статьи
Алгоритм выше описывает обратное распространения градиента решения ОДУ для последовательных наблюдений.
В случае нескольких наблюдений на одну траекторию все рассчитывается так же, но в моменты наблюдений обратно распространенный градиент надо корректировать градиентами от текущего наблюдения, как показано в иллюстрации 1.
Реализация
Код ниже — это моя реализация Нейронных ОДУ. Я делал это сугубо для лучшего понимания того, что происходит. Впрочем, она очень близка к тому, что реализовано в репозитории у авторов статьи. Здесь содержится весь нужный для понимания код в одном месте, он также слегка более закомментированный. Для реального применения и экспериментов все же лучше использовать реализацию авторов оригинальной статьи.
import math import numpy as np from IPython.display import clear_output from tqdm import tqdm_notebook as tqdm import matplotlib as mpl import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns sns.color_palette("bright") import matplotlib as mpl import matplotlib.cm as cm import torch from torch import Tensor from torch import nn from torch.nn import functional as F from torch.autograd import Variable use_cuda = torch.cuda.is_available()
Для начала надо реализовать любой метод эволюции систем ОДУ. В целях простоты здесь реализован метод Эйлера, хотя подойдет любой явный или неявный метод.
def ode_solve(z0, t0, t1, f): """ Простейший метод эволюции ОДУ - метод Эйлера """ h_max = 0.05 n_steps = math.ceil((abs(t1 - t0)/h_max).max().item()) h = (t1 - t0)/n_steps t = t0 z = z0 for i_step in range(n_steps): z = z + h * f(z, t) t = t + h return z
Здесь также описан суперкласс параметризованной функции динамики с парочкой полезных методов.
Во-первых: нужно возвращать все параметры от которых зависит функция в виде вектора.
Во-вторых: надо рассчитывать аугментированную динамику. Эта динамика зависит от градиента параметризованной функции по параметрам и входным данным. Чтобы не приходилось каждый раз для каждой новой архитектуры прописывать градиент руками, воспользуемся методом torch.autograd.grad.
class ODEF(nn.Module): def forward_with_grad(self, z, t, grad_outputs): """Compute f and a df/dz, a df/dp, a df/dt""" batch_size = z.shape[0] out = self.forward(z, t) a = grad_outputs adfdz, adfdt, *adfdp = torch.autograd.grad( (out,), (z, t) + tuple(self.parameters()), grad_outputs=(a), allow_unused=True, retain_graph=True ) # метод grad автоматически суммирует градиенты для всех элементов батча, # надо expand их обратно if adfdp is not None: adfdp = torch.cat([p_grad.flatten() for p_grad in adfdp]).unsqueeze(0) adfdp = adfdp.expand(batch_size, -1) / batch_size if adfdt is not None: adfdt = adfdt.expand(batch_size, 1) / batch_size return out, adfdz, adfdt, adfdp def flatten_parameters(self): p_shapes = [] flat_parameters = [] for p in self.parameters(): p_shapes.append(p.size()) flat_parameters.append(p.flatten()) return torch.cat(flat_parameters)
Код ниже описывает прямое и обратное распространение для Нейронных ОДУ. Приходится отделить этот код от основного torch.nn.Module в виде функции torch.autograd.Function потому, что в последнем можно реализовать произвольный метод обратного распространения, в отличие от модуля. Так что это просто костыль.
Эта функция лежит в основе всего подхода Нейронных ОДУ.
class ODEAdjoint(torch.autograd.Function): @staticmethod def forward(ctx, z0, t, flat_parameters, func): assert isinstance(func, ODEF) bs, *z_shape = z0.size() time_len = t.size(0) with torch.no_grad(): z = torch.zeros(time_len, bs, *z_shape).to(z0) z[0] = z0 for i_t in range(time_len - 1): z0 = ode_solve(z0, t[i_t], t[i_t+1], func) z[i_t+1] = z0 ctx.func = func ctx.save_for_backward(t, z.clone(), flat_parameters) return z @staticmethod def backward(ctx, dLdz): """ dLdz shape: time_len, batch_size, *z_shape """ func = ctx.func t, z, flat_parameters = ctx.saved_tensors time_len, bs, *z_shape = z.size() n_dim = np.prod(z_shape) n_params = flat_parameters.size(0) # Динамика аугментированной системы, # которую надо эволюционировать обратно во времени def augmented_dynamics(aug_z_i, t_i): """ Тензоры здесь - это срезы по времени t_i - тензор с размерами: bs, 1 aug_z_i - тензор с размерами: bs, n_dim*2 + n_params + 1 """ # игнорируем параметры и время z_i, a = aug_z_i[:, :n_dim], aug_z_i[:, n_dim:2*n_dim] # Unflatten z and a z_i = z_i.view(bs, *z_shape) a = a.view(bs, *z_shape) with torch.set_grad_enabled(True): t_i = t_i.detach().requires_grad_(True) z_i = z_i.detach().requires_grad_(True) faug = func.forward_with_grad(z_i, t_i, grad_outputs=a) func_eval, adfdz, adfdt, adfdp = faug adfdz = adfdz if adfdz is not None else torch.zeros(bs, *z_shape) adfdp = adfdp if adfdp is not None else torch.zeros(bs, n_params) adfdt = adfdt if adfdt is not None else torch.zeros(bs, 1) adfdz = adfdz.to(z_i) adfdp = adfdp.to(z_i) adfdt = adfdt.to(z_i) # Flatten f and adfdz func_eval = func_eval.view(bs, n_dim) adfdz = adfdz.view(bs, n_dim) return torch.cat((func_eval, -adfdz, -adfdp, -adfdt), dim=1) dLdz = dLdz.view(time_len, bs, n_dim) # flatten dLdz для удобства with torch.no_grad(): ## Создадим плейсхолдеры для возвращаемых градиентов # Распространенные назад сопряженные состояния, # которые надо поправить градиентами от наблюдений adj_z = torch.zeros(bs, n_dim).to(dLdz) adj_p = torch.zeros(bs, n_params).to(dLdz) # В отличие от z и p, нужно вернуть градиенты для всех моментов времени adj_t = torch.zeros(time_len, bs, 1).to(dLdz) for i_t in range(time_len-1, 0, -1): z_i = z[i_t] t_i = t[i_t] f_i = func(z_i, t_i).view(bs, n_dim) # Рассчитаем прямые градиенты от наблюдений dLdz_i = dLdz[i_t] dLdt_i = torch.bmm(torch.transpose(dLdz_i.unsqueeze(-1), 1, 2), f_i.unsqueeze(-1))[:, 0] # Подправим ими сопряженные состояния adj_z += dLdz_i adj_t[i_t] = adj_t[i_t] - dLdt_i # Упакуем аугментированные переменные в вектор aug_z = torch.cat(( z_i.view(bs, n_dim), adj_z, torch.zeros(bs, n_params).to(z) adj_t[i_t]), dim=-1 ) # Решим (эволюционируем) аугментированную систему назад во времени aug_ans = ode_solve(aug_z, t_i, t[i_t-1], augmented_dynamics) # Распакуем переменные обратно из решенной системы adj_z[:] = aug_ans[:, n_dim:2*n_dim] adj_p[:] += aug_ans[:, 2*n_dim:2*n_dim + n_params] adj_t[i_t-1] = aug_ans[:, 2*n_dim + n_params:] del aug_z, aug_ans ## Подправим сопряженное состояние в нулевой момент прямыми градиентами # Вычислим прямые градиенты dLdz_0 = dLdz[0] dLdt_0 = torch.bmm(torch.transpose(dLdz_0.unsqueeze(-1), 1, 2), f_i.unsqueeze(-1))[:, 0] # Подправим adj_z += dLdz_0 adj_t[0] = adj_t[0] - dLdt_0 return adj_z.view(bs, *z_shape), adj_t, adj_p, None
Теперь для удобства обернем эту функцию в nn.Module.
class NeuralODE(nn.Module): def __init__(self, func): super(NeuralODE, self).__init__() assert isinstance(func, ODEF) self.func = func def forward(self, z0, t=Tensor([0., 1.]), return_whole_sequence=False): t = t.to(z0) z = ODEAdjoint.apply(z0, t, self.func.flatten_parameters(), self.func) if return_whole_sequence: return z else: return z[-1]
Применение
Восстановление реальной функции динамики (проверка подхода)
В качестве базового теста проверим теперь, правда ли Neural ODE могут восстанавливать истинную функцию динамики, используя данные наблюдений.
Для этого мы сначала определим функцию динамики ОДУ, эволюционируем на ее основе траектории, а потом попробуем восстановить ее из случайно параметризованной функции динамики.
Для начала проверим простейший случай линейного ОДУ. Функция динамики это просто действие матрицы.
Обучаемая функция параметризована случайной матрицей.
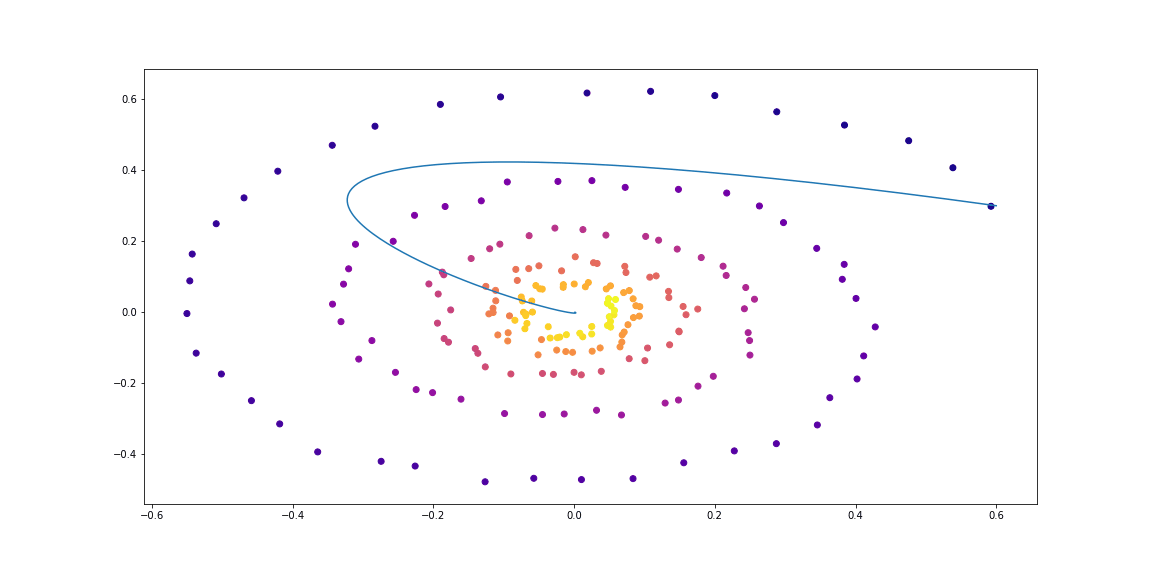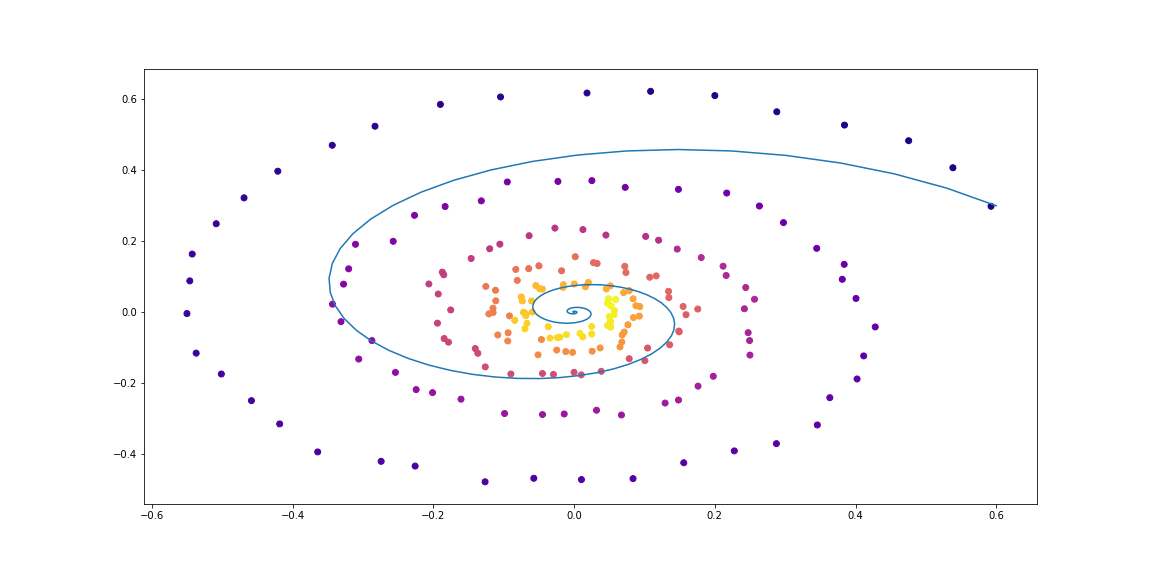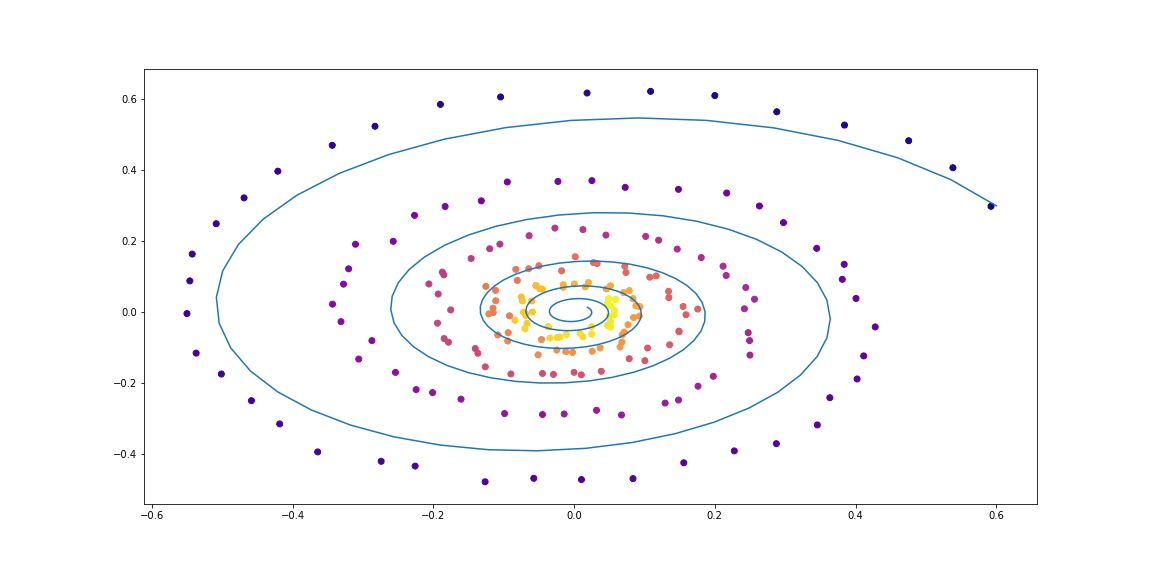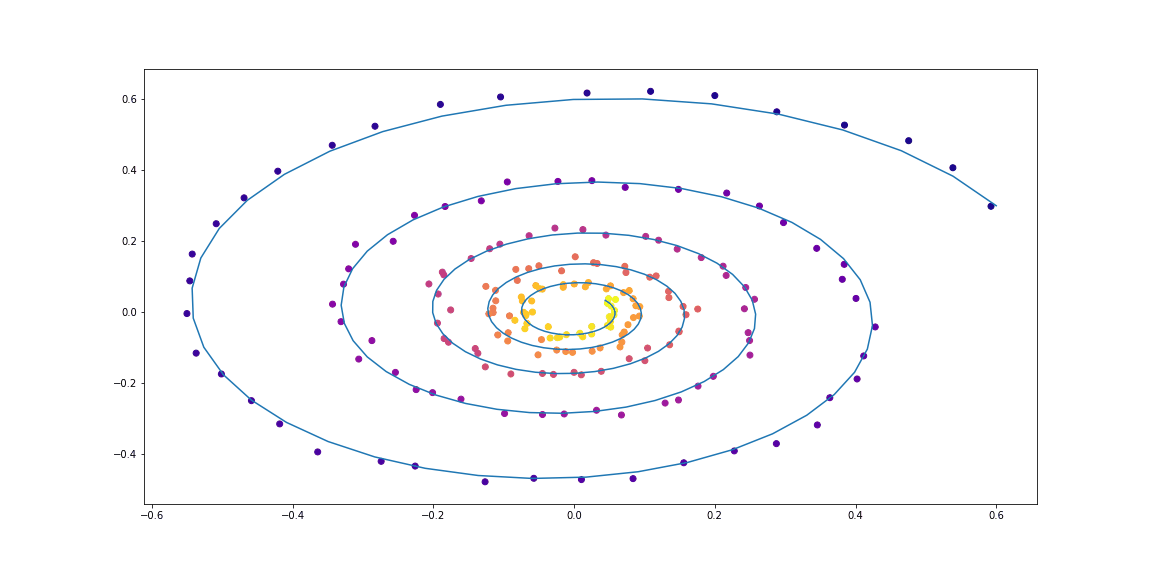
Далее чуть более изощренная динамика (без гифки, потому что процесс обучения не такой красивый :))
Обучаемая функция здесь — это полносвязная сеть с одним скрытым слоем.
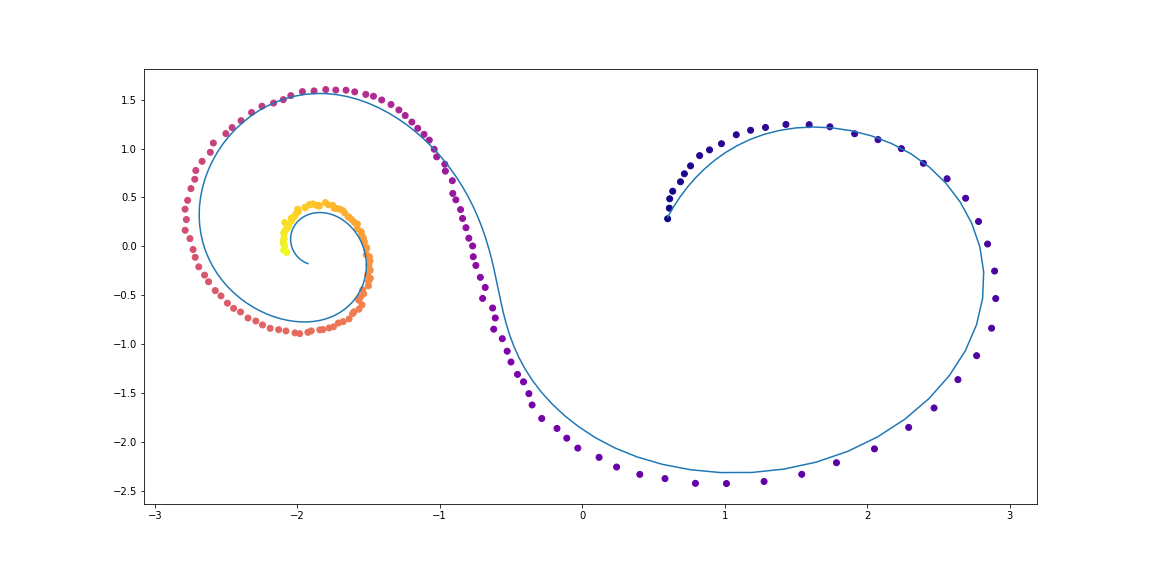
Код
Функция динамики это просто матрица
Случайно параметризованная матрица
Динамика для более изощренных траекторий
Обучаемая динамика в виде полносвязной сети
class LinearODEF(ODEF): def __init__(self, W): super(LinearODEF, self).__init__() self.lin = nn.Linear(2, 2, bias=False) self.lin.weight = nn.Parameter(W) def forward(self, x, t): return self.lin(x)
Функция динамики это просто матрица
class SpiralFunctionExample(LinearODEF): def __init__(self): matrix = Tensor([[-0.1, -1.], [1., -0.1]]) super(SpiralFunctionExample, self).__init__(matrix)
Случайно параметризованная матрица
class RandomLinearODEF(LinearODEF): def __init__(self): super(RandomLinearODEF, self).__init__(torch.randn(2, 2)/2.)
Динамика для более изощренных траекторий
class TestODEF(ODEF): def __init__(self, A, B, x0): super(TestODEF, self).__init__() self.A = nn.Linear(2, 2, bias=False) self.A.weight = nn.Parameter(A) self.B = nn.Linear(2, 2, bias=False) self.B.weight = nn.Parameter(B) self.x0 = nn.Parameter(x0) def forward(self, x, t): xTx0 = torch.sum(x*self.x0, dim=1) dxdt = torch.sigmoid(xTx0) * self.A(x - self.x0) + torch.sigmoid(-xTx0) * self.B(x + self.x0) return dxdt
Обучаемая динамика в виде полносвязной сети
class NNODEF(ODEF): def __init__(self, in_dim, hid_dim, time_invariant=False): super(NNODEF, self).__init__() self.time_invariant = time_invariant if time_invariant: self.lin1 = nn.Linear(in_dim, hid_dim) else: self.lin1 = nn.Linear(in_dim+1, hid_dim) self.lin2 = nn.Linear(hid_dim, hid_dim) self.lin3 = nn.Linear(hid_dim, in_dim) self.elu = nn.ELU(inplace=True) def forward(self, x, t): if not self.time_invariant: x = torch.cat((x, t), dim=-1) h = self.elu(self.lin1(x)) h = self.elu(self.lin2(h)) out = self.lin3(h) return out def to_np(x): return x.detach().cpu().numpy() def plot_trajectories(obs=None, times=None, trajs=None, save=None, figsize=(16, 8)): plt.figure(figsize=figsize) if obs is not None: if times is None: times = [None] * len(obs) for o, t in zip(obs, times): o, t = to_np(o), to_np(t) for b_i in range(o.shape[1]): plt.scatter(o[:, b_i, 0], o[:, b_i, 1], c=t[:, b_i, 0], cmap=cm.plasma) if trajs is not None: for z in trajs: z = to_np(z) plt.plot(z[:, 0, 0], z[:, 0, 1], lw=1.5) if save is not None: plt.savefig(save) plt.show() def conduct_experiment(ode_true, ode_trained, n_steps, name, plot_freq=10): # Create data z0 = Variable(torch.Tensor([[0.6, 0.3]])) t_max = 6.29*5 n_points = 200 index_np = np.arange(0, n_points, 1, dtype=np.int) index_np = np.hstack([index_np[:, None]]) times_np = np.linspace(0, t_max, num=n_points) times_np = np.hstack([times_np[:, None]]) times = torch.from_numpy(times_np[:, :, None]).to(z0) obs = ode_true(z0, times, return_whole_sequence=True).detach() obs = obs + torch.randn_like(obs) * 0.01 # Get trajectory of random timespan min_delta_time = 1.0 max_delta_time = 5.0 max_points_num = 32 def create_batch(): t0 = np.random.uniform(0, t_max - max_delta_time) t1 = t0 + np.random.uniform(min_delta_time, max_delta_time) idx = sorted(np.random.permutation( index_np[(times_np > t0) & (times_np < t1)] )[:max_points_num]) obs_ = obs[idx] ts_ = times[idx] return obs_, ts_ # Train Neural ODE optimizer = torch.optim.Adam(ode_trained.parameters(), lr=0.01) for i in range(n_steps): obs_, ts_ = create_batch() z_ = ode_trained(obs_[0], ts_, return_whole_sequence=True) loss = F.mse_loss(z_, obs_.detach()) optimizer.zero_grad() loss.backward(retain_graph=True) optimizer.step() if i % plot_freq == 0: z_p = ode_trained(z0, times, return_whole_sequence=True) plot_trajectories(obs=[obs], times=[times], trajs=[z_p], save=f"assets/imgs/{name}/{i}.png") clear_output(wait=True) ode_true = NeuralODE(SpiralFunctionExample()) ode_trained = NeuralODE(RandomLinearODEF()) conduct_experiment(ode_true, ode_trained, 500, "linear") func = TestODEF(Tensor([[-0.1, -0.5], [0.5, -0.1]]), Tensor([[0.2, 1.], [-1, 0.2]]), Tensor([[-1., 0.]])) ode_true = NeuralODE(func) func = NNODEF(2, 16, time_invariant=True) ode_trained = NeuralODE(func) conduct_experiment(ode_true, ode_trained, 3000, "comp", plot_freq=30)
Как можно видеть, Neural ODE довольно хорошо справляются с восстановлением динамики. То есть концепция в целом работает.
Теперь проверим на чуть более сложной задаче (MNIST, ха-ха).
Neural ODE вдохновленные ResNets
В ResNet’ax скрытое состояние меняется по формуле
где
В пределе, если брать бесконечное число блоков со все меньшими шагами, мы получаем непрерывную динамику скрытого слоя в виде ОДУ, прямо как то, что было выше.
Начиная со входного слоя
Теперь мы можем считать
Проверка Neural ODE архитектуры на MNIST
В этой части мы проверим возможность Neural ODE быть использованными в виде компонентов в более привычных архитектурах.
В частности, мы заменим остаточные (residual) блоки на Neural ODE в классификаторе MNIST.

Код
def norm(dim): return nn.BatchNorm2d(dim) def conv3x3(in_feats, out_feats, stride=1): return nn.Conv2d(in_feats, out_feats, kernel_size=3, stride=stride, padding=1, bias=False) def add_time(in_tensor, t): bs, c, w, h = in_tensor.shape return torch.cat((in_tensor, t.expand(bs, 1, w, h)), dim=1) class ConvODEF(ODEF): def __init__(self, dim): super(ConvODEF, self).__init__() self.conv1 = conv3x3(dim + 1, dim) self.norm1 = norm(dim) self.conv2 = conv3x3(dim + 1, dim) self.norm2 = norm(dim) def forward(self, x, t): xt = add_time(x, t) h = self.norm1(torch.relu(self.conv1(xt))) ht = add_time(h, t) dxdt = self.norm2(torch.relu(self.conv2(ht))) return dxdt class ContinuousNeuralMNISTClassifier(nn.Module): def __init__(self, ode): super(ContinuousNeuralMNISTClassifier, self).__init__() self.downsampling = nn.Sequential( nn.Conv2d(1, 64, 3, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), ) self.feature = ode self.norm = norm(64) self.avg_pool = nn.AdaptiveAvgPool2d((1, 1)) self.fc = nn.Linear(64, 10) def forward(self, x): x = self.downsampling(x) x = self.feature(x) x = self.norm(x) x = self.avg_pool(x) shape = torch.prod(torch.tensor(x.shape[1:])).item() x = x.view(-1, shape) out = self.fc(x) return out func = ConvODEF(64) ode = NeuralODE(func) model = ContinuousNeuralMNISTClassifier(ode) if use_cuda: model = model.cuda() import torchvision img_std = 0.3081 img_mean = 0.1307 batch_size = 32 train_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=True, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=batch_size, shuffle=True ) test_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=False, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=128, shuffle=True ) optimizer = torch.optim.Adam(model.parameters()) def train(epoch): num_items = 0 train_losses = [] model.train() criterion = nn.CrossEntropyLoss() print(f"Training Epoch {epoch}...") for batch_idx, (data, target) in tqdm(enumerate(train_loader), total=len(train_loader)): if use_cuda: data = data.cuda() target = target.cuda() optimizer.zero_grad() output = model(data) loss = criterion(output, target) loss.backward() optimizer.step() train_losses += [loss.item()] num_items += data.shape[0] print('Train loss: {:.5f}'.format(np.mean(train_losses))) return train_losses def test(): accuracy = 0.0 num_items = 0 model.eval() criterion = nn.CrossEntropyLoss() print(f"Testing...") with torch.no_grad(): for batch_idx, (data, target) in tqdm(enumerate(test_loader), total=len(test_loader)): if use_cuda: data = data.cuda() target = target.cuda() output = model(data) accuracy += torch.sum(torch.argmax(output, dim=1) == target).item() num_items += data.shape[0] accuracy = accuracy * 100 / num_items print("Test Accuracy: {:.3f}%".format(accuracy)) n_epochs = 5 test() train_losses = [] for epoch in range(1, n_epochs + 1): train_losses += train(epoch) test() import pandas as pd plt.figure(figsize=(9, 5)) history = pd.DataFrame({"loss": train_losses}) history["cum_data"] = history.index * batch_size history["smooth_loss"] = history.loss.ewm(halflife=10).mean() history.plot(x="cum_data", y="smooth_loss", figsize=(12, 5), title="train error")
Testing... 100% 79/79 [00:01<00:00, 45.69it/s] Test Accuracy: 9.740% Training Epoch 1... 100% 1875/1875 [01:15<00:00, 24.69it/s] Train loss: 0.20137 Testing... 100% 79/79 [00:01<00:00, 46.64it/s] Test Accuracy: 98.680% Training Epoch 2... 100% 1875/1875 [01:17<00:00, 24.32it/s] Train loss: 0.05059 Testing... 100% 79/79 [00:01<00:00, 46.11it/s] Test Accuracy: 97.760% Training Epoch 3... 100% 1875/1875 [01:16<00:00, 24.63it/s] Train loss: 0.03808 Testing... 100% 79/79 [00:01<00:00, 45.65it/s] Test Accuracy: 99.000% Training Epoch 4... 100% 1875/1875 [01:17<00:00, 24.28it/s] Train loss: 0.02894 Testing... 100% 79/79 [00:01<00:00, 45.42it/s] Test Accuracy: 99.130% Training Epoch 5... 100% 1875/1875 [01:16<00:00, 24.67it/s] Train loss: 0.02424 Testing... 100% 79/79 [00:01<00:00, 45.89it/s] Test Accuracy: 99.170%

После очень грубой тренировки в течение всего 5 эпох и 6 минут обучения, модель уже достигла тестовой ошибки в менее, чем 1%. Можно сказать, что Нейронные ОДУ хорошо интегрируются в виде компонента в более традиционные сети.
В своей статье авторы также сравнивают этот классификатор (ODE-Net) с обычной полнозвязной сетью, с ResNet’ом с похожей архитектурой, и с точно такой же архитектурой, только в которой градиент распространяется напрямую через операции в ODESolve (без метода сопряженного градиента) (RK-Net).

Иллюстрация из оригинальной статьи
Согласно им, 1-слойная полносвязная сеть с примерно таким же количеством параметров как Neural ODE имеет намного более высокую ошибку на тесте, ResNet с примерно такой же ошибкой имеет намного больше параметров, а RK-Net без метода сопряженного градиента, имеет чуть более высокую ошибку и с линейно растущим потреблением памяти (чем меньше допустимая ошибка, тем больше шагов должен сделать ODESolve, что линейно увеличивает потребляемую память с числом шагов).
Авторы в своей имплементации используют неявный метод Рунге-Кутты с адаптивным размером шага, в отличие от простейшего метода Эйлера здесь. Они также изучают некоторые свойства новой архитектуры.

Характеристика ODE-Net (NFE Forward — количество вычислений функции при прямом проходе)
Иллюстрация из оригинальной статьи
- (a) Изменение допустимого уровня численной ошибки изменяет количество шагов в прямом распространении.
- (b) Время потраченное на прямое распространение пропорционально количеству вычислений функции.
- (с) Количество вычислений функции при обратном распространение составляет примерно половину от прямого распространения, это указывает на то, что метод сопряженного градиента может быть более вычислительно эффективным, чем распространение градиента напрямую через ODESolve.
- (d) Как ODE-Net становится все более и более обученным, он требует все больше вычислений функции (все меньший шаг), возможно адаптируясь под возрастающую сложность модели.
Скрытая генеративная функция для моделирования временного ряда
Neural ODE подходит для обработки непрерывных последовательных данных и тогда, когда траектория лежит в неизвестном скрытом пространстве.
В этом разделе мы поэкспериментируем в генерации непрерывных последовательностей, используя Neural ODE, и немножко посмотрим на выученное скрытое пространство.
Авторы также сравнивают это с аналогичными последовательностями, сгенерированными Рекуррентными сетями.
Эксперимент здесь слегка отличается от соответствующего примера в репозитории авторов, здесь более разнообразное множество траекторий.
Данные
Обучающие данные состоят из случайных спиралей, половина из которых направлены по часовой, а вторая — против часовой. Далее случайные подпоследовательности сэмплируются из этих спиралей, обрабатываются кодирующей рекуррентной моделью в обратном направлении, порождая стартовое скрытое состояние, которое затем эволюционирует, создавая траекторию в скрытом пространстве. Это скрытая траектория затем отображается в пространство данных и сравнивается с сэмплированной подпоследовательностью. Таким образом, модель учится генерировать траектории, похожие на датасет.
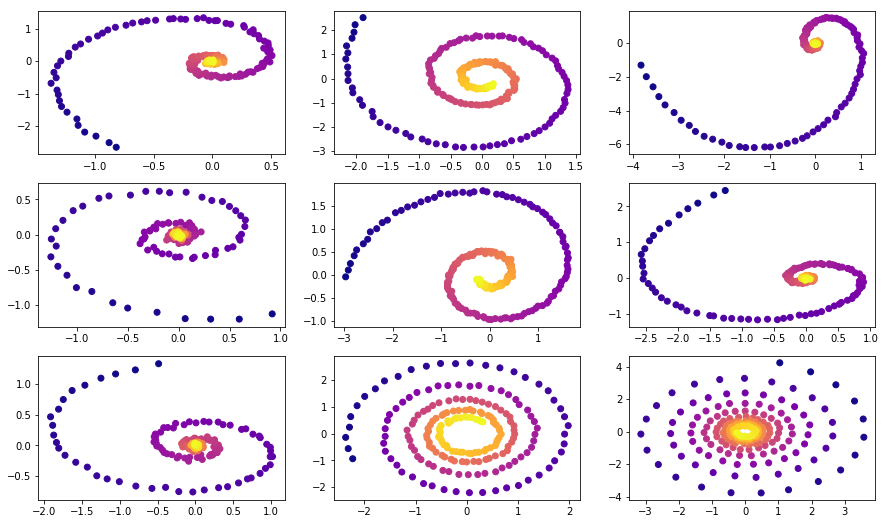
Примеры спиралей из датасета
VAE как генеративная модель
Генеративная модель через процедуру сэмплирования:
Которая может быть обучена, используя подход вариационных автокодировщиков.
- Пройтись рекуррентным энкодером через временную последовательность назад во времени, чтобы получить параметры
,
вариационного апостериорного распределения, а потом сэмплировать из него:
- Получить скрытую траекторию:
- Отобразить скрытую траекторию в траекторию в данных, используя другую нейросеть:
- Максимизировать оценку нижней границы обоснованности (ELBO) для сэмплированной траектории:
И в случае Гауссовского апостериорного распределения
Граф вычислений скрытой ОДУ модели можно изобразить вот так

Иллюстрация из оригинальной статьи
Эту модель можно затем протестировать на то, как она интерполирует траекторию, используя только начальные наблюдения.
Код
Define models
class RNNEncoder(nn.Module): def __init__(self, input_dim, hidden_dim, latent_dim): super(RNNEncoder, self).__init__() self.input_dim = input_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim self.rnn = nn.GRU(input_dim+1, hidden_dim) self.hid2lat = nn.Linear(hidden_dim, 2*latent_dim) def forward(self, x, t): # Concatenate time to input t = t.clone() t[1:] = t[:-1] - t[1:] t[0] = 0. xt = torch.cat((x, t), dim=-1) _, h0 = self.rnn(xt.flip((0,))) # Reversed # Compute latent dimension z0 = self.hid2lat(h0[0]) z0_mean = z0[:, :self.latent_dim] z0_log_var = z0[:, self.latent_dim:] return z0_mean, z0_log_var class NeuralODEDecoder(nn.Module): def __init__(self, output_dim, hidden_dim, latent_dim): super(NeuralODEDecoder, self).__init__() self.output_dim = output_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim func = NNODEF(latent_dim, hidden_dim, time_invariant=True) self.ode = NeuralODE(func) self.l2h = nn.Linear(latent_dim, hidden_dim) self.h2o = nn.Linear(hidden_dim, output_dim) def forward(self, z0, t): zs = self.ode(z0, t, return_whole_sequence=True) hs = self.l2h(zs) xs = self.h2o(hs) return xs class ODEVAE(nn.Module): def __init__(self, output_dim, hidden_dim, latent_dim): super(ODEVAE, self).__init__() self.output_dim = output_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim self.encoder = RNNEncoder(output_dim, hidden_dim, latent_dim) self.decoder = NeuralODEDecoder(output_dim, hidden_dim, latent_dim) def forward(self, x, t, MAP=False): z_mean, z_log_var = self.encoder(x, t) if MAP: z = z_mean else: z = z_mean + torch.randn_like(z_mean) * torch.exp(0.5 * z_log_var) x_p = self.decoder(z, t) return x_p, z, z_mean, z_log_var def generate_with_seed(self, seed_x, t): seed_t_len = seed_x.shape[0] z_mean, z_log_var = self.encoder(seed_x, t[:seed_t_len]) x_p = self.decoder(z_mean, t) return x_p
Генерация датасета
t_max = 6.29*5 n_points = 200 noise_std = 0.02 num_spirals = 1000 index_np = np.arange(0, n_points, 1, dtype=np.int) index_np = np.hstack([index_np[:, None]]) times_np = np.linspace(0, t_max, num=n_points) times_np = np.hstack([times_np[:, None]] * num_spirals) times = torch.from_numpy(times_np[:, :, None]).to(torch.float32) # Generate random spirals parameters normal01 = torch.distributions.Normal(0, 1.0) x0 = Variable(normal01.sample((num_spirals, 2))) * 2.0 W11 = -0.1 * normal01.sample((num_spirals,)).abs() - 0.05 W22 = -0.1 * normal01.sample((num_spirals,)).abs() - 0.05 W21 = -1.0 * normal01.sample((num_spirals,)).abs() W12 = 1.0 * normal01.sample((num_spirals,)).abs() xs_list = [] for i in range(num_spirals): if i % 2 == 1: # Make it counter-clockwise W21, W12 = W12, W21 func = LinearODEF(Tensor([[W11[i], W12[i]], [W21[i], W22[i]]])) ode = NeuralODE(func) xs = ode(x0[i:i+1], times[:, i:i+1], return_whole_sequence=True) xs_list.append(xs) orig_trajs = torch.cat(xs_list, dim=1).detach() samp_trajs = orig_trajs + torch.randn_like(orig_trajs) * noise_std samp_ts = times fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(15, 9)) axes = axes.flatten() for i, ax in enumerate(axes): ax.scatter(samp_trajs[:, i, 0], samp_trajs[:, i, 1], c=samp_ts[:, i, 0], cmap=cm.plasma) plt.show() import numpy.random as npr def gen_batch(batch_size, n_sample=100): n_batches = samp_trajs.shape[1] // batch_size time_len = samp_trajs.shape[0] n_sample = min(n_sample, time_len) for i in range(n_batches): if n_sample > 0: probs = [1. / (time_len - n_sample)] * (time_len - n_sample) t0_idx = npr.multinomial(1, probs) t0_idx = np.argmax(t0_idx) tM_idx = t0_idx + n_sample else: t0_idx = 0 tM_idx = time_len frm, to = batch_size*i, batch_size*(i+1) yield samp_trajs[t0_idx:tM_idx, frm:to], samp_ts[t0_idx:tM_idx, frm:to]
Обучение
vae = ODEVAE(2, 64, 6) vae = vae.cuda() if use_cuda: vae = vae.cuda() optim = torch.optim.Adam(vae.parameters(), betas=(0.9, 0.999), lr=0.001) preload = False n_epochs = 20000 batch_size = 100 plot_traj_idx = 1 plot_traj = orig_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_obs = samp_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_ts = samp_ts[:, plot_traj_idx:plot_traj_idx+1] if use_cuda: plot_traj = plot_traj.cuda() plot_obs = plot_obs.cuda() plot_ts = plot_ts.cuda() if preload: vae.load_state_dict(torch.load("models/vae_spirals.sd")) for epoch_idx in range(n_epochs): losses = [] train_iter = gen_batch(batch_size) for x, t in train_iter: optim.zero_grad() if use_cuda: x, t = x.cuda(), t.cuda() max_len = np.random.choice([30, 50, 100]) permutation = np.random.permutation(t.shape[0]) np.random.shuffle(permutation) permutation = np.sort(permutation[:max_len]) x, t = x[permutation], t[permutation] x_p, z, z_mean, z_log_var = vae(x, t) z_var = torch.exp(z_log_var) kl_loss = -0.5 * torch.sum(1 + z_log_var - z_mean**2 - z_var, -1) loss = 0.5 * ((x-x_p)**2).sum(-1).sum(0) / noise_std**2 + kl_loss loss = torch.mean(loss) loss /= max_len loss.backward() optim.step() losses.append(loss.item()) print(f"Epoch {epoch_idx}") frm, to, to_seed = 0, 200, 50 seed_trajs = samp_trajs[frm:to_seed] ts = samp_ts[frm:to] if use_cuda: seed_trajs = seed_trajs.cuda() ts = ts.cuda() samp_trajs_p = to_np(vae.generate_with_seed(seed_trajs, ts)) fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(15, 9)) axes = axes.flatten() for i, ax in enumerate(axes): ax.scatter(to_np(seed_trajs[:, i, 0]), to_np(seed_trajs[:, i, 1]), c=to_np(ts[frm:to_seed, i, 0]), cmap=cm.plasma) ax.plot(to_np(orig_trajs[frm:to, i, 0]), to_np(orig_trajs[frm:to, i, 1])) ax.plot(samp_trajs_p[:, i, 0], samp_trajs_p[:, i, 1]) plt.show() print(np.mean(losses), np.median(losses)) clear_output(wait=True) spiral_0_idx = 3 spiral_1_idx = 6 homotopy_p = Tensor(np.linspace(0., 1., 10)[:, None]) vae = vae if use_cuda: homotopy_p = homotopy_p.cuda() vae = vae.cuda() spiral_0 = orig_trajs[:, spiral_0_idx:spiral_0_idx+1, :] spiral_1 = orig_trajs[:, spiral_1_idx:spiral_1_idx+1, :] ts_0 = samp_ts[:, spiral_0_idx:spiral_0_idx+1, :] ts_1 = samp_ts[:, spiral_1_idx:spiral_1_idx+1, :] if use_cuda: spiral_0, ts_0 = spiral_0.cuda(), ts_0.cuda() spiral_1, ts_1 = spiral_1.cuda(), ts_1.cuda() z_cw, _ = vae.encoder(spiral_0, ts_0) z_cc, _ = vae.encoder(spiral_1, ts_1) homotopy_z = z_cw * (1 - homotopy_p) + z_cc * homotopy_p t = torch.from_numpy(np.linspace(0, 6*np.pi, 200)) t = t[:, None].expand(200, 10)[:, :, None].cuda() t = t.cuda() if use_cuda else t hom_gen_trajs = vae.decoder(homotopy_z, t) fig, axes = plt.subplots(nrows=2, ncols=5, figsize=(15, 5)) axes = axes.flatten() for i, ax in enumerate(axes): ax.plot(to_np(hom_gen_trajs[:, i, 0]), to_np(hom_gen_trajs[:, i, 1])) plt.show() torch.save(vae.state_dict(), "models/vae_spirals.sd")
Вот что получается после ночи обучения

Точки — это зашумленные наблюдения оригинальной траектории (синий),
желтая — это реконструированная и интерполированная траектория, используя точки как входы.
Цвет точки показывает время.
Реконструкции некоторых примеров не выглядят слишком хорошими. Может модель недостаточно сложная или недостаточно долго училась. В любом случае реконструкции выглядят очень разумно.
Теперь посмотрим что будет, если интерполировать скрытую переменную по-часовой траектории к противо-часовой траектории.

Авторы также сравнивают реконструкции и интерполяции траекторий между Neural ODE и простой Рекуррентной сетью.

Иллюстрация из оригинальной статьи
Непрерывные Нормализующие Потоки
Оригинальная статья также привносит многое в тему Нормализующих Потоков. Нормализующие потоки используются, когда нужно сэмплировать из некоторого сложного распределения, появившегося через замену переменных от некоторого простого распределения (Гауссовского, например), и при этом все еще знать плотность вероятности в точке каждого сэмпла.
Авторы показывают, что использование непрерывной замены переменных намного более вычислительно эффективно и интерпретируемо, чем предыдущие методы.
Нормализующие потоки очень полезны в таких моделях как Вариационные Автокодировщики, Байесовские Нейронные Сети и других из Байесовского подхода.
Эта тема, впрочем, лежит за пределами данной статьи, и тем, кто заинтересовался, следует прочесть оригинальную научную статью.
Для затравки:

Визуализация трансформации из шума (простого распределения) в данные (сложное распределение) для двух датасетов;
Ось-X показывает трансформацию плотности и сэмплов с течением «времени» (для ННП) и «глубины» (для НП).
Иллюстрация из оригинальной статьи
Спасибо bekemax за помощь в правке английской версии текста и за интересные физические комментарии.
Это завершает мое небольшое исследование Neural ODEs. Спасибо за внимание!
