Пришла мне в голову немного странная мысль, что дом мог бы быть неплохой площадкой для игры в Тетрис. Недалеко от меня как раз располагалось одно подходящее для этого здание. Результат можно увидеть на видео:
Проект реализован на достаточно низком уровне, без использования какого-то уже готового решения.
Исходный код
Чаще всего сейчас используют 2 варианта реализации дополненной реальности:
Данные реализации не требуют особой подготовки или особых условий.
Есть еще один вариант реализации — распознавать конкретный объект и использовать его в качестве маркера. Это требует как минимум его наличия, но дает возможность визуально им управлять. Один из способов такого распознавания — детектирование объекта по ребрам. У него есть ограничения — у объекта-маркера должны быть четко определяемые края, т.е. объект должен быть скорее всего однотонным.
Либо края должны быть четко очерчены, как, например, подсветка этого здания:

Видно, что подсветку легко можно будет отделить на изображении и использовать ее для детектирования.
На Qt. Этот фреймворк позволяет работать на разных платформах и при этом на С++. Так как нам важна производительность, то плюсы кажутся очевидным выбором.
Хотя Qt не очень хорошо работал с android (долгий запуск, подглючивала отладка), но это все нивелировалось возможностью отлаживать алгоритм на десктопе.
Трехмерная графика визуализировалась на сыром OpenGL, встроенном в Qt.
Работа с камерой велась через средства Qt. Для отладки был записан ролик, и было достаточно удобно заменять видеопоток камеры видеопотоком с файла.
Вывод осуществлялся через средства qml. Подружить qml и OpenGL получилось не без проблем, но не будем на этом останавливаться.
Для обработки изображений подключена библиотека OpenCV.
Теперь перейдем к самому интересному — к алгоритму трекинга объекта по его ребрам.
И начнем с выделения ребер на изображении. Все ребра в нашем случае имеют вид прямых линий, поэтому первая мысль, которая приходит на ум — использовать детектор линий. В качестве детектора линий можно было бы использовать преобразования Хафа. Однако, это путь мне кажется не очень верным, так как преобразование Хафа довольно затратное, к тому же данный детектор не очень надежный (это субъективно, возможно все зависит от задачи).
Вместо этого пойдем другим, более общим путем. Не будем брать в расчет, что линии у нас прямые, а будем работать просто на бинарном изображении. В бинарное изображение будет закодировано наличие ребер. Т.е. пиксель со значением равным нулю означает, что в этом месте есть ребро, значение пикселя больше нуля — тут ребра нет. Такое изображение можно получить при помощи детектора границ Канни или при помощи простого порогового преобразования. Эти алгоритмы можно найти в OpenCV.
Также в OpenCV есть еще одна полезная для нас сейчас функция — distanceTransform, которая на входе принимает бинарное изображение, а на выходе дает изображение, в пикселях которого закодировано расстояние до ближайшего нулевого пикселя.
Теперь предположим, что у нас уже есть первое хорошее приближение того, где у нас должна находиться наша модель. Далее, опишем функцию ошибки, которая описывает насколько ребра нашего приближения не совпадают с ребрами на полученном изображении. При помощи изображения от distanceTransform мы уже в состоянии это сделать. А затем запустим алгоритм оптимизации функции, меняя только наше приближение положения объекта в пространстве. В результате наше приближение должно достаточно точно описывать реальное положение объекта.
В итоге алгоритм можно разделить на два этапа:
На этом этапе на необходимо выделить ребра на изображении. Можно использовать детектор границ Канни, но в нашем случае лучше работает обычное пороговое преобразование или адаптивная его версия (в OpenCV это функции threshold или adaptiveThreshold). Понятно, что на таком изображении будет шум, поэтому нужна фильтрация. Выполним ее следующим образом — выделим контура при помощи функции OpenCV findCountours и удалим сегменты, которые имеют слишком маленький размер или недостаточно похожи на линию.
Результат обработки можно увидеть на изображении:

Последовательно: исходное изображение -> после порогового преобразования -> после фильтрации.
Это изображении уже достаточно четко говорит нам, где есть нужное ребро, а где нет. После этого применяем функцию distanceTransform, и в результате у нас будет информация о том, как далеко каждая точка находится от ребра. Полученное изображение обозначим как .
.
Вот так оно выглядит, если его нормализовать и визуализировать:

Далее нам понадобятся некоторые математические инструменты.
Оптимизация функции — это задача нахождения минимума функции.
Если мы имеем дело с линейной системой уравнений, то найти минимум достаточно просто. Представим систему уравнений в матричном виде: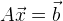 , тогда наше решение:
, тогда наше решение: 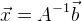 . Если же у нас переопределенная система уравнений, то можно воспользоваться методом наименьших квадратов:
. Если же у нас переопределенная система уравнений, то можно воспользоваться методом наименьших квадратов:  .
.
Если же наша функция нелинейна, то задача усложняется. Для нахождения минимума можно воспользоваться алгоритмом Гаусса-Ньютона. Алгоритм работает следующим образом:
Разберем алгоритм немного подробнее.
Пусть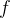 — рабочая функция,
— рабочая функция, 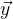 — известный заранее вектор значений функции. При наличии идеального решения уравнения
— известный заранее вектор значений функции. При наличии идеального решения уравнения  справедливо следующее утверждение
справедливо следующее утверждение  . Но у нас есть только его приближение
. Но у нас есть только его приближение 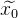 . Тогда вектор ошибки от данного приближения обозначим как:
. Тогда вектор ошибки от данного приближения обозначим как:  . А общая ошибка функции будет:
. А общая ошибка функции будет: 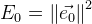 . Теперь отыскав такой
. Теперь отыскав такой  , при котором
, при котором  будет достигать минимума, мы получим лучшее приближение решения
будет достигать минимума, мы получим лучшее приближение решения  .
.
Начиная с приближения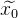 мы итеративно будем его приближать, получая на каждой итерации
мы итеративно будем его приближать, получая на каждой итерации  . Для этого нам понадобится каждую итерацию вычислять матрицу Якоби для функции
. Для этого нам понадобится каждую итерацию вычислять матрицу Якоби для функции 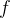 для текущего приближения, состоящую из производных нашей функции:
для текущего приближения, состоящую из производных нашей функции:

И следующее приближение задается как: .
.
Часто задачи строятся таким образом, что мы имеем большое количество независимых друг от друга данных (только от значений ). В результате общая матрица Якоби получается очень разряженной. Есть способ оптимизировать вычисления.
). В результате общая матрица Якоби получается очень разряженной. Есть способ оптимизировать вычисления.
Предположим общая функция у нас вычисляется из набора точек. От j-ой точки получаем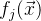 . Вместо того, чтобы вычислять матрицу Якоби
. Вместо того, чтобы вычислять матрицу Якоби 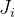 для всей функции, вычислим матрицу Якоби конкретно для
для всей функции, вычислим матрицу Якоби конкретно для 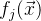 и обозначим ее как:
и обозначим ее как:  . Тогда следующее приближение будет задаваться следующим образом:
. Тогда следующее приближение будет задаваться следующим образом:  . Кроме того, данное изменение позволяет распараллелить вычисления.
. Кроме того, данное изменение позволяет распараллелить вычисления.
Может так получиться, что следующее значение будет давать большую ошибку, чем
будет давать большую ошибку, чем  . Для решения этой проблемы можно воспользоваться модификацией алгоритма — алгоритмом Левенберга-Марквардта. Добавим значение
. Для решения этой проблемы можно воспользоваться модификацией алгоритма — алгоритмом Левенберга-Марквардта. Добавим значение  в нашу формулу:
в нашу формулу: 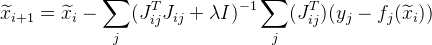 , где
, где 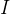 — это единичная матрица. Значение
— это единичная матрица. Значение  подбирается следующим образом:
подбирается следующим образом:
Чем более нелинейна функция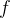 , тем больше должно быть значение
, тем больше должно быть значение  . Однако чем больше значение
. Однако чем больше значение  , тем медленнее сходится алгоритм.
, тем медленнее сходится алгоритм.
Завершаем алгоритм, когда отличается от
отличается от  на достаточно малую величину и берем
на достаточно малую величину и берем  в качестве решения.
в качестве решения.
Алгоритм достаточно универсален и может быть использован для самых разных задач.
Раз уж мы имеем дело с координатами в пространстве, то понятно, что нам нужно уметь этими координатами манипулировать. Предположим, что у нас есть некоторый набор точек . И нам нужно их повернуть вокруг точки с нулевыми координатами. Вероятно проще всего будет использовать матрицу поворота R, описывающую необходимый поворот:
. И нам нужно их повернуть вокруг точки с нулевыми координатами. Вероятно проще всего будет использовать матрицу поворота R, описывающую необходимый поворот:  . Если нам нужно сместить точки, то просто прибавим нужный вектор t:
. Если нам нужно сместить точки, то просто прибавим нужный вектор t:  .
.
Таким образом, можно как угодно менять положение объекта пространстве. Выходит, что координаты объекта задаются трехмерной матрицей R и трехмерным вектором t, т.е. 12 параметров. При этом эти параметры не независимы между собой, компоненты матрицы поворота связаны между собой определенными условиями. Поэтому с точки зрения использования в оптимизации функции эти параметры является не лучшим решением. Параметров больше, чем степеней свободы, есть зависимость между ними. Есть другая форма поворота — формула поворота Родрига. Этот поворот задается тремя параметрами, образуя трехмерный вектор.
Нормализованный вектор — это ось поворота, а длина этого вектора — угол поворота вокруг этой оси.
Зададим функцию поворот вектора v: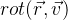 , используя параметры r формулы Родрига. Получаем из этого следующую формулу:
, используя параметры r формулы Родрига. Получаем из этого следующую формулу: 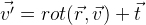 .
.
И в итоге мы можем задать координаты положения объекта 6-мерным вектором: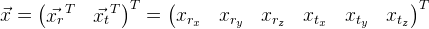
Получаем следующую формулу: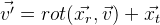 .
.
Теперь опишем простую математическую модель камеры, используемую в проекте:
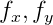 — фокальное расстояние в пикселях;
— фокальное расстояние в пикселях; 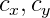 — оптический центр также в пикселях. Это индивидуальные параметры камеры, которые называют внутренними параметрами камеры (intrinsic parameters of camera). Обычно эти параметры известны заранее. В данном проекте эти параметры подобраны на глаз.
— оптический центр также в пикселях. Это индивидуальные параметры камеры, которые называют внутренними параметрами камеры (intrinsic parameters of camera). Обычно эти параметры известны заранее. В данном проекте эти параметры подобраны на глаз.
Данная модель не учитывает линзовые искажения камер (дисторсию). Предположим, что их нет.
Данной моделью мы получаем центральную проекцию, все точки которой тем больше стремятся к оптическому центру, чем дальше от камеры они находится. Таким образом получаем эффект сужающийся железной дороги:

В пространстве камера сонаправлена с осью z, плоскость изображения параллельна плоскости xy. Дополним нашу модель возможностью перемещаться в пространстве:
Таким образом мы получили модель, при помощи которой мы можем в алгебраической форме моделировать проецирование точек из внешнего мира на изображение камеры (из мировых координат в экранные). Неизвестными в этой модели для нас остаются параметры относительного положения камеры в пространстве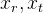 . Эти параметры называют внешними характеристиками камеры (extrinsic parameters of camera).
. Эти параметры называют внешними характеристиками камеры (extrinsic parameters of camera).
Реализован уже без средств OpenCV. Для начала нам нужно получить функцию ошибки для нашего приближенного решения, о которой писалось выше. И распишем ее вычисление поэтапно:
Теперь осталось найти минимум E. Для этого воспользуемся описанным выше алгоритмом Левенберга-Марквардта. Как мы уже знаем, алгоритм требует вычисления матрицы Якоби, т.е. производные функции. Можно использовать численное нахождение производных. Можно также использовать какие-то готовые решения этого алгоритма. Однако, в данном проекте все писалось вручную, поэтому я опишу полный вывод всего решения.
Для каждой контрольной точки мы получаем независимое от других точек уравнение. Выше уже было описано, что можно в таком случае рассматривать эти уравнения независимо друг от друга, вычисляя матрицу Якоби конкретно для каждого. Разберем его по порядку, используя правила дифференцирования сложной функции:

Обозначим , тогда
, тогда 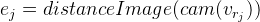

Отсюда:

Далее обозначим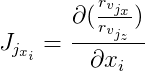 и
и  , тогда:
, тогда:

Производные по изображению distanceImage находятся численно. А для вычисления векторов и
и  нужно будет найти производные по формуле поворота Родрига. Якобиан по этой формуле я нашел в публикации «A compact formula for the derivative of a 3-D rotation in
нужно будет найти производные по формуле поворота Родрига. Якобиан по этой формуле я нашел в публикации «A compact formula for the derivative of a 3-D rotation in
exponential coordinates» Guillermo Gallego, Anthony Yezzi:
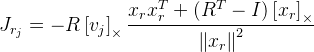 ,
,
где R — матрица поворота полученная по формуле Родрига из вектора поворота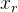 ;
;  — точка, которую поворачиваем;I — единичная матрица;
— точка, которую поворачиваем;I — единичная матрица;  . Как мы здесь видим, у нас есть деление на длину вектора поворота, и если вектор нулевой, то формула уже не работает. Вероятно это связано с тем, что при нулевом векторе не определена ось поворота. Если вектор поворота очень близок к нулевому, то используем уже эту формулу:
. Как мы здесь видим, у нас есть деление на длину вектора поворота, и если вектор нулевой, то формула уже не работает. Вероятно это связано с тем, что при нулевом векторе не определена ось поворота. Если вектор поворота очень близок к нулевому, то используем уже эту формулу: 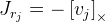 .
.
Осталось расписать и
и  (здесь индекс j опущен):
(здесь индекс j опущен):
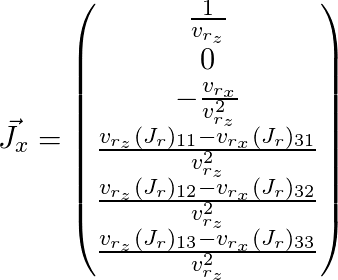

Таким образом мы получили матрицу Якоби для нужной нам точки и можем использовать его для алгоритма оптимизации, описанного выше.
Есть несколько проблемы с этим алгоритмом. Во-первых — точность. В результате глобальное положение камеры немного скачет от кадра к кадру. Можно немного это поправить. У нас есть априорная информация, что положение камеры не может резко меняться от кадра к кадру. И мы можем уменьшить это дрожание, добавив дополнительные уравнения в функцию.
Следует помнить, что вектор смещение t не является в нашем случае координатой глобального положения камеры. Глобальное положение является локальной точкой с нулевыми координатами, поэтому его можно вывести следующим образом:
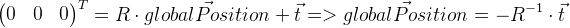
Запоминаем положение предыдущего кадра в prevGlobalPosition. Теперь предыдущее положение должно быть близко к нулю, т.е. длина вектора должна быть достаточно мала. Т.е. нужно минимизировать кроме прочих значений несоответствий еще и вектор d. Чтобы определить степень влияния этой модификации, введем значение
должна быть достаточно мала. Т.е. нужно минимизировать кроме прочих значений несоответствий еще и вектор d. Чтобы определить степень влияния этой модификации, введем значение  и умножим перед добавлением вектор d на
и умножим перед добавлением вектор d на  :
:  . Т.е. в алгоритме оптимизации дополнительно минимизируем вектор d’. Разумеется для этого необходимо будет вычислить для него матрицу Якоби, которая выводится таким же образом, как мы уже выводили ее выше для общей функции ошибки.
. Т.е. в алгоритме оптимизации дополнительно минимизируем вектор d’. Разумеется для этого необходимо будет вычислить для него матрицу Якоби, которая выводится таким же образом, как мы уже выводили ее выше для общей функции ошибки.
Вторая проблема алгоритма — он может застревать в локальных минимумах. В других работах это проблема решается использованием particle filter. В нашем же случае и этого варианта оказалось, в принципе, достаточно.
Зная положение и форму объекта, можно ими визуально манипулировать, что я и попытался продемонстрировать на видео. Искажение объекта происходило при помощи шейдеров OpenGL. При помощи нашей модели я проецировал точку объекта на изображение, и таким образом получал цвет этой точки. После чего можно эту точку двигать, получая интересные эффекты — например, морфинг. Однако, нужно помнить, что смещая точку, нужно, чтобы что-то оставалось на ее месте, иначе станут заметны несоответствия. Кроме того, в зависимости от качества нашего трекинга и формы объекта, мы будем получать разные нежелательные эффекты из-за накопленных ошибок, которые все равно будут. Просто это нужно как-то учитывать. В представленном выше видео мне хотелось показать, что дополненную реальность можно использовать немного шире, чем просто накладывать виртуальные объекты на изображение.
Кстати говоря, в Vuforia SDK реализован трекинг объекта по его форме, правда я не думаю, что с ней бы получилось реализовать данный проект, так как нет возможности использовать строго определенные ребра и нельзя их связать с подсветкой здания.
Проект реализован на достаточно низком уровне, без использования какого-то уже готового решения.
Исходный код
Чаще всего сейчас используют 2 варианта реализации дополненной реальности:
- безмаркерная, т.е. положение камеры определяется по движению ключевых точек ее видеопотока;
- изображение в качестве маркера, относительно которого находится положение камеры.
Данные реализации не требуют особой подготовки или особых условий.
Есть еще один вариант реализации — распознавать конкретный объект и использовать его в качестве маркера. Это требует как минимум его наличия, но дает возможность визуально им управлять. Один из способов такого распознавания — детектирование объекта по ребрам. У него есть ограничения — у объекта-маркера должны быть четко определяемые края, т.е. объект должен быть скорее всего однотонным.
Либо края должны быть четко очерчены, как, например, подсветка этого здания:

Видно, что подсветку легко можно будет отделить на изображении и использовать ее для детектирования.
Реализация
На Qt. Этот фреймворк позволяет работать на разных платформах и при этом на С++. Так как нам важна производительность, то плюсы кажутся очевидным выбором.
Хотя Qt не очень хорошо работал с android (долгий запуск, подглючивала отладка), но это все нивелировалось возможностью отлаживать алгоритм на десктопе.
Трехмерная графика визуализировалась на сыром OpenGL, встроенном в Qt.
Работа с камерой велась через средства Qt. Для отладки был записан ролик, и было достаточно удобно заменять видеопоток камеры видеопотоком с файла.
Вывод осуществлялся через средства qml. Подружить qml и OpenGL получилось не без проблем, но не будем на этом останавливаться.
Для обработки изображений подключена библиотека OpenCV.
Алгоритм трекинга
Теперь перейдем к самому интересному — к алгоритму трекинга объекта по его ребрам.
И начнем с выделения ребер на изображении. Все ребра в нашем случае имеют вид прямых линий, поэтому первая мысль, которая приходит на ум — использовать детектор линий. В качестве детектора линий можно было бы использовать преобразования Хафа. Однако, это путь мне кажется не очень верным, так как преобразование Хафа довольно затратное, к тому же данный детектор не очень надежный (это субъективно, возможно все зависит от задачи).
Вместо этого пойдем другим, более общим путем. Не будем брать в расчет, что линии у нас прямые, а будем работать просто на бинарном изображении. В бинарное изображение будет закодировано наличие ребер. Т.е. пиксель со значением равным нулю означает, что в этом месте есть ребро, значение пикселя больше нуля — тут ребра нет. Такое изображение можно получить при помощи детектора границ Канни или при помощи простого порогового преобразования. Эти алгоритмы можно найти в OpenCV.
Также в OpenCV есть еще одна полезная для нас сейчас функция — distanceTransform, которая на входе принимает бинарное изображение, а на выходе дает изображение, в пикселях которого закодировано расстояние до ближайшего нулевого пикселя.
Теперь предположим, что у нас уже есть первое хорошее приближение того, где у нас должна находиться наша модель. Далее, опишем функцию ошибки, которая описывает насколько ребра нашего приближения не совпадают с ребрами на полученном изображении. При помощи изображения от distanceTransform мы уже в состоянии это сделать. А затем запустим алгоритм оптимизации функции, меняя только наше приближение положения объекта в пространстве. В результате наше приближение должно достаточно точно описывать реальное положение объекта.
В итоге алгоритм можно разделить на два этапа:
- Препроцесинг изображения — бинаризация, фильтрация, и применение функции distanceTransfrom.
- Трекинг — оптимизация функции ошибки.
Препроцессинг изображения
На этом этапе на необходимо выделить ребра на изображении. Можно использовать детектор границ Канни, но в нашем случае лучше работает обычное пороговое преобразование или адаптивная его версия (в OpenCV это функции threshold или adaptiveThreshold). Понятно, что на таком изображении будет шум, поэтому нужна фильтрация. Выполним ее следующим образом — выделим контура при помощи функции OpenCV findCountours и удалим сегменты, которые имеют слишком маленький размер или недостаточно похожи на линию.
Результат обработки можно увидеть на изображении:

Последовательно: исходное изображение -> после порогового преобразования -> после фильтрации.
Это изображении уже достаточно четко говорит нам, где есть нужное ребро, а где нет. После этого применяем функцию distanceTransform, и в результате у нас будет информация о том, как далеко каждая точка находится от ребра. Полученное изображение обозначим как
 .
.Вот так оно выглядит, если его нормализовать и визуализировать:

Далее нам понадобятся некоторые математические инструменты.
Алгоритм оптимизации функции
Оптимизация функции — это задача нахождения минимума функции.
Если мы имеем дело с линейной системой уравнений, то найти минимум достаточно просто. Представим систему уравнений в матричном виде:
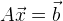 , тогда наше решение:
, тогда наше решение: 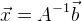 . Если же у нас переопределенная система уравнений, то можно воспользоваться методом наименьших квадратов:
. Если же у нас переопределенная система уравнений, то можно воспользоваться методом наименьших квадратов:  .
.Если же наша функция нелинейна, то задача усложняется. Для нахождения минимума можно воспользоваться алгоритмом Гаусса-Ньютона. Алгоритм работает следующим образом:
- Предполагается, что у нас есть уже какое-то начальное приближение решения
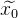 , которое мы будем итеративно уточнять.
, которое мы будем итеративно уточнять. - Используя разложение Тейлора мы можем аппроксимировать нашу нелинейную функцию линейной в точке текущего приближения. Решаем полученную линейную систему уравнений методом наименьших квадратов, получая
 . В результате полученное решение не будет являться решением, но оно будет ближе, чем текущие приближение.
. В результате полученное решение не будет являться решением, но оно будет ближе, чем текущие приближение. - Заменяем текущее приближение
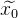 полученным решением
полученным решением  и переходим к шагу 2. Так повторяем до тех пор, пока разница между
и переходим к шагу 2. Так повторяем до тех пор, пока разница между  и
и  не станет меньше определенного значения.
не станет меньше определенного значения.
Разберем алгоритм немного подробнее.
Пусть
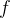 — рабочая функция,
— рабочая функция, 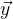 — известный заранее вектор значений функции. При наличии идеального решения уравнения
— известный заранее вектор значений функции. При наличии идеального решения уравнения  справедливо следующее утверждение
справедливо следующее утверждение  . Но у нас есть только его приближение
. Но у нас есть только его приближение 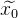 . Тогда вектор ошибки от данного приближения обозначим как:
. Тогда вектор ошибки от данного приближения обозначим как:  . А общая ошибка функции будет:
. А общая ошибка функции будет: 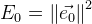 . Теперь отыскав такой
. Теперь отыскав такой  , при котором
, при котором  будет достигать минимума, мы получим лучшее приближение решения
будет достигать минимума, мы получим лучшее приближение решения  .
.Начиная с приближения
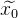 мы итеративно будем его приближать, получая на каждой итерации
мы итеративно будем его приближать, получая на каждой итерации  . Для этого нам понадобится каждую итерацию вычислять матрицу Якоби для функции
. Для этого нам понадобится каждую итерацию вычислять матрицу Якоби для функции 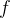 для текущего приближения, состоящую из производных нашей функции:
для текущего приближения, состоящую из производных нашей функции:
И следующее приближение задается как:
 .
.Часто задачи строятся таким образом, что мы имеем большое количество независимых друг от друга данных (только от значений
 ). В результате общая матрица Якоби получается очень разряженной. Есть способ оптимизировать вычисления.
). В результате общая матрица Якоби получается очень разряженной. Есть способ оптимизировать вычисления. Предположим общая функция у нас вычисляется из набора точек. От j-ой точки получаем
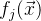 . Вместо того, чтобы вычислять матрицу Якоби
. Вместо того, чтобы вычислять матрицу Якоби 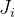 для всей функции, вычислим матрицу Якоби конкретно для
для всей функции, вычислим матрицу Якоби конкретно для 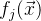 и обозначим ее как:
и обозначим ее как:  . Тогда следующее приближение будет задаваться следующим образом:
. Тогда следующее приближение будет задаваться следующим образом:  . Кроме того, данное изменение позволяет распараллелить вычисления.
. Кроме того, данное изменение позволяет распараллелить вычисления. Может так получиться, что следующее значение
 будет давать большую ошибку, чем
будет давать большую ошибку, чем  . Для решения этой проблемы можно воспользоваться модификацией алгоритма — алгоритмом Левенберга-Марквардта. Добавим значение
. Для решения этой проблемы можно воспользоваться модификацией алгоритма — алгоритмом Левенберга-Марквардта. Добавим значение  в нашу формулу:
в нашу формулу: 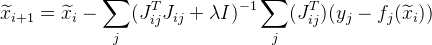 , где
, где 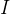 — это единичная матрица. Значение
— это единичная матрица. Значение  подбирается следующим образом:
подбирается следующим образом:- сперва она имеет какое-то достаточно малое значение (такое, чтобы алгоритм сходился);
- затем, если ошибка для
 больше, чем
больше, чем  , то увеличиваем значение
, то увеличиваем значение  и пробуем подсчитать ошибку для
и пробуем подсчитать ошибку для  снова.
снова.
Чем более нелинейна функция
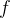 , тем больше должно быть значение
, тем больше должно быть значение  . Однако чем больше значение
. Однако чем больше значение  , тем медленнее сходится алгоритм.
, тем медленнее сходится алгоритм.Завершаем алгоритм, когда
 отличается от
отличается от  на достаточно малую величину и берем
на достаточно малую величину и берем  в качестве решения.
в качестве решения.Алгоритм достаточно универсален и может быть использован для самых разных задач.
Математическая модель трекинга
Раз уж мы имеем дело с координатами в пространстве, то понятно, что нам нужно уметь этими координатами манипулировать. Предположим, что у нас есть некоторый набор точек
 . И нам нужно их повернуть вокруг точки с нулевыми координатами. Вероятно проще всего будет использовать матрицу поворота R, описывающую необходимый поворот:
. И нам нужно их повернуть вокруг точки с нулевыми координатами. Вероятно проще всего будет использовать матрицу поворота R, описывающую необходимый поворот:  . Если нам нужно сместить точки, то просто прибавим нужный вектор t:
. Если нам нужно сместить точки, то просто прибавим нужный вектор t:  .
.Таким образом, можно как угодно менять положение объекта пространстве. Выходит, что координаты объекта задаются трехмерной матрицей R и трехмерным вектором t, т.е. 12 параметров. При этом эти параметры не независимы между собой, компоненты матрицы поворота связаны между собой определенными условиями. Поэтому с точки зрения использования в оптимизации функции эти параметры является не лучшим решением. Параметров больше, чем степеней свободы, есть зависимость между ними. Есть другая форма поворота — формула поворота Родрига. Этот поворот задается тремя параметрами, образуя трехмерный вектор.
Нормализованный вектор — это ось поворота, а длина этого вектора — угол поворота вокруг этой оси.
Зададим функцию поворот вектора v:
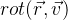 , используя параметры r формулы Родрига. Получаем из этого следующую формулу:
, используя параметры r формулы Родрига. Получаем из этого следующую формулу: 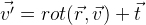 .
.И в итоге мы можем задать координаты положения объекта 6-мерным вектором:
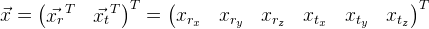
Получаем следующую формулу:
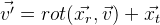 .
.Pinhole camera model
Теперь опишем простую математическую модель камеры, используемую в проекте:
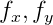 — фокальное расстояние в пикселях;
— фокальное расстояние в пикселях; 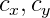 — оптический центр также в пикселях. Это индивидуальные параметры камеры, которые называют внутренними параметрами камеры (intrinsic parameters of camera). Обычно эти параметры известны заранее. В данном проекте эти параметры подобраны на глаз.
— оптический центр также в пикселях. Это индивидуальные параметры камеры, которые называют внутренними параметрами камеры (intrinsic parameters of camera). Обычно эти параметры известны заранее. В данном проекте эти параметры подобраны на глаз.Данная модель не учитывает линзовые искажения камер (дисторсию). Предположим, что их нет.
Данной моделью мы получаем центральную проекцию, все точки которой тем больше стремятся к оптическому центру, чем дальше от камеры они находится. Таким образом получаем эффект сужающийся железной дороги:

В пространстве камера сонаправлена с осью z, плоскость изображения параллельна плоскости xy. Дополним нашу модель возможностью перемещаться в пространстве:
Таким образом мы получили модель, при помощи которой мы можем в алгебраической форме моделировать проецирование точек из внешнего мира на изображение камеры (из мировых координат в экранные). Неизвестными в этой модели для нас остаются параметры относительного положения камеры в пространстве
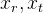 . Эти параметры называют внешними характеристиками камеры (extrinsic parameters of camera).
. Эти параметры называют внешними характеристиками камеры (extrinsic parameters of camera). Трекинг
Реализован уже без средств OpenCV. Для начала нам нужно получить функцию ошибки для нашего приближенного решения, о которой писалось выше. И распишем ее вычисление поэтапно:
- Выбираем такие ребра модели трекинга, которые являются видимыми исходя из параметров текущего приближения.
- Выбранный набор ребер превращаем в фиксированный набор точек, для упрощения вычислений. Можно, например, с каждого ребра взять n-ое количество точек, либо (более правильный вариант) подобрать такое количество, чтобы между точками было фиксированное расстояние в пикселях. Назовем их контрольными точками (в проекте: controlPoint — контрольные точки и controlPixelDistance — то самое фиксированное расстояние в пикселях).
- Проецируем контрольные точки на изображение. Благодаря distanceImage мы можем получить расстояние проекции контрольной точки до ребра на изображении. В идеальном случае все контрольные точки должны лежать строго на ребрах изображения, т.е. расстояние до ребра должно быть равным нулю. Исходя из этого получаем ошибку для конкретной контрольной точки:
 .
. - Получаем такую функцию ошибки:
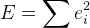
Теперь осталось найти минимум E. Для этого воспользуемся описанным выше алгоритмом Левенберга-Марквардта. Как мы уже знаем, алгоритм требует вычисления матрицы Якоби, т.е. производные функции. Можно использовать численное нахождение производных. Можно также использовать какие-то готовые решения этого алгоритма. Однако, в данном проекте все писалось вручную, поэтому я опишу полный вывод всего решения.
Для каждой контрольной точки мы получаем независимое от других точек уравнение. Выше уже было описано, что можно в таком случае рассматривать эти уравнения независимо друг от друга, вычисляя матрицу Якоби конкретно для каждого. Разберем его по порядку, используя правила дифференцирования сложной функции:

Обозначим
 , тогда
, тогда 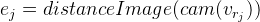

Отсюда:

Далее обозначим
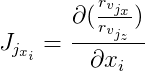 и
и  , тогда:
, тогда: 
Производные по изображению distanceImage находятся численно. А для вычисления векторов
 и
и  нужно будет найти производные по формуле поворота Родрига. Якобиан по этой формуле я нашел в публикации «A compact formula for the derivative of a 3-D rotation in
нужно будет найти производные по формуле поворота Родрига. Якобиан по этой формуле я нашел в публикации «A compact formula for the derivative of a 3-D rotation inexponential coordinates» Guillermo Gallego, Anthony Yezzi:
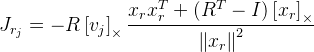 ,
, где R — матрица поворота полученная по формуле Родрига из вектора поворота
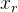 ;
;  — точка, которую поворачиваем;I — единичная матрица;
— точка, которую поворачиваем;I — единичная матрица;  . Как мы здесь видим, у нас есть деление на длину вектора поворота, и если вектор нулевой, то формула уже не работает. Вероятно это связано с тем, что при нулевом векторе не определена ось поворота. Если вектор поворота очень близок к нулевому, то используем уже эту формулу:
. Как мы здесь видим, у нас есть деление на длину вектора поворота, и если вектор нулевой, то формула уже не работает. Вероятно это связано с тем, что при нулевом векторе не определена ось поворота. Если вектор поворота очень близок к нулевому, то используем уже эту формулу: 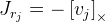 .
.Осталось расписать
 и
и  (здесь индекс j опущен):
(здесь индекс j опущен):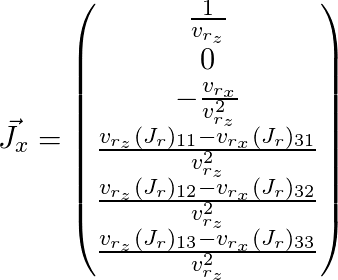

Таким образом мы получили матрицу Якоби для нужной нам точки и можем использовать его для алгоритма оптимизации, описанного выше.
Есть несколько проблемы с этим алгоритмом. Во-первых — точность. В результате глобальное положение камеры немного скачет от кадра к кадру. Можно немного это поправить. У нас есть априорная информация, что положение камеры не может резко меняться от кадра к кадру. И мы можем уменьшить это дрожание, добавив дополнительные уравнения в функцию.
Следует помнить, что вектор смещение t не является в нашем случае координатой глобального положения камеры. Глобальное положение является локальной точкой с нулевыми координатами, поэтому его можно вывести следующим образом:
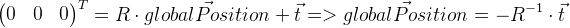
Запоминаем положение предыдущего кадра в prevGlobalPosition. Теперь предыдущее положение должно быть близко к нулю, т.е. длина вектора
 должна быть достаточно мала. Т.е. нужно минимизировать кроме прочих значений несоответствий еще и вектор d. Чтобы определить степень влияния этой модификации, введем значение
должна быть достаточно мала. Т.е. нужно минимизировать кроме прочих значений несоответствий еще и вектор d. Чтобы определить степень влияния этой модификации, введем значение  и умножим перед добавлением вектор d на
и умножим перед добавлением вектор d на  :
:  . Т.е. в алгоритме оптимизации дополнительно минимизируем вектор d’. Разумеется для этого необходимо будет вычислить для него матрицу Якоби, которая выводится таким же образом, как мы уже выводили ее выше для общей функции ошибки.
. Т.е. в алгоритме оптимизации дополнительно минимизируем вектор d’. Разумеется для этого необходимо будет вычислить для него матрицу Якоби, которая выводится таким же образом, как мы уже выводили ее выше для общей функции ошибки. Вторая проблема алгоритма — он может застревать в локальных минимумах. В других работах это проблема решается использованием particle filter. В нашем же случае и этого варианта оказалось, в принципе, достаточно.
Бонусы от трекинга объекта
Зная положение и форму объекта, можно ими визуально манипулировать, что я и попытался продемонстрировать на видео. Искажение объекта происходило при помощи шейдеров OpenGL. При помощи нашей модели я проецировал точку объекта на изображение, и таким образом получал цвет этой точки. После чего можно эту точку двигать, получая интересные эффекты — например, морфинг. Однако, нужно помнить, что смещая точку, нужно, чтобы что-то оставалось на ее месте, иначе станут заметны несоответствия. Кроме того, в зависимости от качества нашего трекинга и формы объекта, мы будем получать разные нежелательные эффекты из-за накопленных ошибок, которые все равно будут. Просто это нужно как-то учитывать. В представленном выше видео мне хотелось показать, что дополненную реальность можно использовать немного шире, чем просто накладывать виртуальные объекты на изображение.
Кстати говоря, в Vuforia SDK реализован трекинг объекта по его форме, правда я не думаю, что с ней бы получилось реализовать данный проект, так как нет возможности использовать строго определенные ребра и нельзя их связать с подсветкой здания.
