
Кто найдет тут «сет», получит от меня шоколадку.
Сет — гениальная игра в которую мы рубились лет 5 назад. Крики, вопли, фотографирование комбинаций.
В правилах игры написано, что ее изобрела в 1991 году генетик Марша Фалко (Marsha Falco), делая пометки во время исследования эпилепсии у немецких овчарок в 1974 году. Для тех, у кого мозг достаточно изможден математикой, через какое-то время возникает подозрение, что есть тут какие-то отголоски с планиметрией и проведением прямых через точки. (Для заданных двух карт существует одна и только одна карта, входящая с ними в один сет.)

Марша Фалко как бы спрашивает: «Ну что, не нашел „сет“?»
Вспоминаем правила
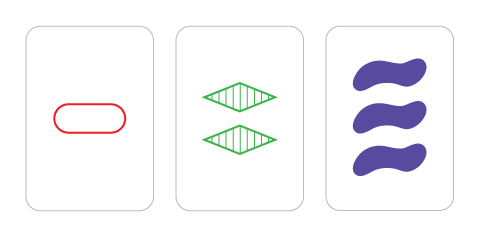
Сет — это карточная игра. Все карты имеют четыре параметра, каждый из которых принимает три значения (итого 3 x 3 × 3 × 3 = 81 карта).

Виды и значения параметров таковы:
- фигура ::= эллипс | ромб | «сопля»
- цвет ::= красный | зелёный | фиолетовый
- заливка ::= белая | полосатая | сплошная
- количество ::= 1 | 2 | 3
Цель игры состоит в нахождении особых сочетаний из трёх карт. Три карты называются «сет», если по каждому из четырёх атрибутов карты либо все одинаковы, либо все различны.
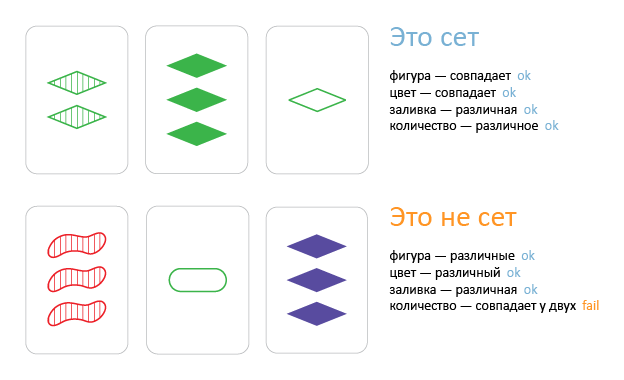
Другими словами можно сказать, что три карты не будут составлять сет, если две карты имеют одно значение параметра, а третья — другое. Можно видеть, что для любых двух карт всегда найдётся третья (притом единственная), с которой они будут сетом.
Ход игры: ведущий выкладывает на стол 12 карт. Когда кто-либо находит сет, он кричит «Сет!» и потом спокойно забирает составляющие сет карты. Если же в выложенных картах сета нет (скорее вcего, только кажется, что нет), ведущий выкладывает ещё три карты.
Максимальное количество карт без сета равно 20. Раунд продолжается, пока не кончилась колода. Выигрывает тот, кто собрал больше сетов.
Математики подсуетились и представили комбинацию из 20 карточек. Кто считает себя Чаком Норрисом, может забыть эту картинку и попробовать собрать «пасьянс» без сета самостоятельно.
Или проверить, а вдруг тут всё-таки есть «сет»?
20 карт без сета

Удобно проверить, что нет «сета по цвету».

Те же карты, но расположение показывает что нес сетов по параметру «заливки».

По количеству.

По фигурам.

Нет сета по различию признаков.
Открытая нерешенная задача математики
Сколько максимально можно карточек выложить, чтобы не получилось ни одного «сета»? Признак имеет три значения.
при 1 «признаке» — 2 карточки
2 признака — 4 карточки
3 признака — 9 карточек
4 признака — 20 карточек
5 признаков — 45 карточек
6 признаков — 112 карточек
7 признаков — хз
А при «n→∞»?
Видео
Создатель игры:
Алексей Савватеев искромётно рассказывает про Сет:
