Пусть будет некий абстрактный эксперимент в процессе которого может происходить некое событие. Этот эксперимент провели пять раз, и в четырех из них происходило то самое событие. Какие выводы можно сделать из этих 4/5?

Есть формула Бернулли, которая дает ответ, с какой вероятностью происходит 4 из 5 при известной исходной вероятности. Но она не дает ответ, какая была исходная вероятность, если событий получилось 4 из 5. Оставим пока в стороне формулу Бернулли.
Сделаем маленькую простенькую программку, симулирующую процессы вероятностей для такого случая, и на основе результата вычислений построим график.
Код этой программы можно найти здесь, рядом же вспомогательные функции.
Полученный расчет закинул в эксель и сделал график.

Такой вариант графика можно назвать распределением плотности вероятностей значения вероятности. Его площадь равна единице, которая распределена в этом холмике.
Для полноты картины упомяну, что этот график соответствует графику по формуле Бернулли от параметра вероятность и умноженный на N+1 количества экспериментов.
Далее по тексту, там где в статье употребляю дробь вида k/n, то это не деление, это k событий из n экспериментов, чтобы каждый раз не писать k из n.
Далее. Можно увеличить количество экспериментов, и получить более узкую область расположения основных величин значения вероятность, но как бы их не увеличивали, эта область не сократится до нулевой области с точно известной вероятностью.
На графике ниже изображены распределения для величин 4/5, 7/9, 11/14 и 24/30. Чем уже область, тем выше холмик, площадь которого неизменная единица. Эти соотношения выбраны, потому что они все около 0.8, а не потому что именно такие могут возникнут при 0.8 исходной вероятности. Выбраны, чтобы продемонстрировать, какая область возможных значений остается даже при 30 проведенных экспериментах.
Код программы для этого графика здесь.

Из чего следует, что в действительности экспериментальную вероятность абсолютно точно не определить, а можно лишь предположить область возможного расположения таковой величины, с точностью в зависимости от того сколько произвели замеров.
Сколько бы экспериментов не провели, всегда остается вероятность, что исходная вероятность может оказаться и 0.0001 и 0.9999. Для упрощения крайние маловероятные значения отбрасываются. И берется, скажем, например 95% от основной площади графика распределения.
Такая штука называется доверительные интервалы. Каких-либо рекомендаций, сколько именно и почему процентов нужно оставить я не встречал. Для прогноза погоды берут поменьше, для запуска космических шаттлов побольше. Так же обычно не упоминают, какой все же используется доверительный интервал на вероятность событий и используется ли вообще.
В моей программе расчет границ доверительного интервала осуществляется здесь.
Получилось, что вероятность события определяется плотностью вероятностей значения вероятности, и на это еще нужно наложить процент области основных значений, чтобы можно было хоть что-то определенно сказать, какая все же вероятность у исследуемого события.
Пусть будет всем надоевшая монетка, подбрасываем эту монетку, и получаем 4 из 5 выпадений решкой — очень реальный случай. В действительности это не совсем то же самое, что описал чуть выше. Чем это отличается от предыдущего эксперимента?
Предыдущий эксперимент описывался из предположения, что вероятность события может быть равнораспределена на интервале от 0 до 1. В программе это задается строкой double probability = get_random_real_0_1();. Но не бывает монеток с вероятностью выпадения, скажем, 0.1 или 0.9 всегда одной стороной.
Если взять тысячу самых разных монет от обычных до самых кривых, и для каждой произвести замер выпадения путем подбрасывания их по тысяче и более раз, то это покажет, что реально они выпадают одной стороной в диапазоне от 0.4 до 0.6 (это числа навскидку, не буду же я выискивать 1000 монет и каждую подбрасывать 1000 раз).
Как этот факт меняет программу для симуляции вероятностей одной конкретной монеты, для которой получили 4 из 5 выпадения решкой?
Допустим, что распределение выпадения одной стороной для монет описывается как приближение к графику нормального распределения взятого с параметрами средняя = 0.5, стандартное отклонение = 0.1. (на графике ниже он изображен черным цветом).
Когда в программе меняю генерацию исходной вероятности с равнораспределенной на распределенную по указанному правилу, то получаю следующие графики:
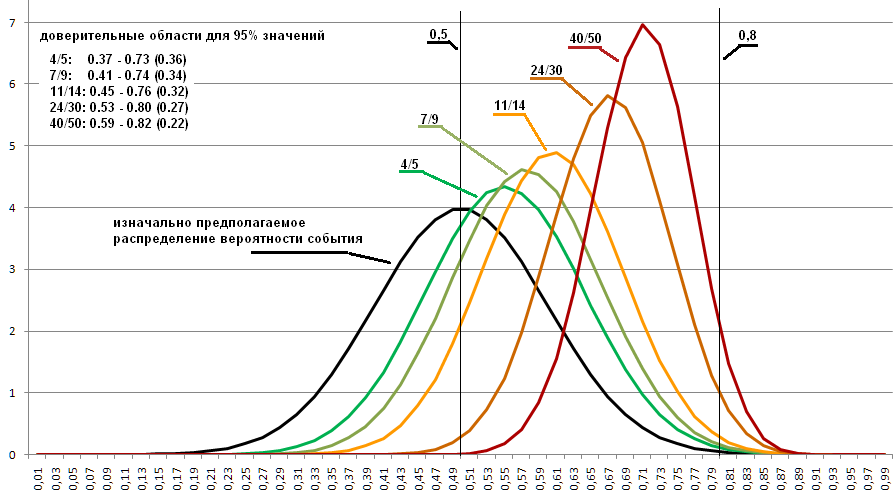
Код этого варианта здесь.
Видно, что распределения сильно сдвинулись и теперь определяют несколько иную область, в которой высоковероятно возможна искомая вероятность. Поэтому, если известно, какие вероятности бывают для тех вещей, одну из которых хотим измерить, то это может несколько улучшить результат.
В итоге, 4/5 это ни о чем не говорит и даже 50 проведенных экспериментов не очень информативны. Это очень мало информации, чтобы определить, что за вероятность все же лежит в основе эксперимента.
== Update ==
Как упомянул в комментариях jzha, человек существенно знающий математику, данные графики можно построить и путем точных формул. Но цель данной статьи все же как можно наглядней показать как образуется то, что все в повседневной жизни называют вероятностью.
Для того что бы это строить путем точных формул, это нужно рассмотреть имеющиеся в наличии данные по распределению вероятностей всех монет через аппроксимацию бета распределением, и путем сопряжения распределений выводить уже расчеты. Такая схема это существенный объем по объяснениям, как это сделать, и если я это здесь буду описывать, то это получится скорее статья по математическим расчетам, а не про бытовые вероятности.
Как получить в формулах описанный частный случай с монетой, смотрите комментарии от jzha.

Есть формула Бернулли, которая дает ответ, с какой вероятностью происходит 4 из 5 при известной исходной вероятности. Но она не дает ответ, какая была исходная вероятность, если событий получилось 4 из 5. Оставим пока в стороне формулу Бернулли.
Сделаем маленькую простенькую программку, симулирующую процессы вероятностей для такого случая, и на основе результата вычислений построим график.
void test1() {
uint sz_ar_events = 50; // замеряемых точек графика
uint ar_events[sz_ar_events]; // в этом массиве сбор данных для графика
for (uint i = 0; i < sz_ar_events; ++i) ar_events[i] = 0;
uint cnt_events = 0; // сколько уже событий в точках графика
uint k = 4; // k событий из n экспериментов
uint n = 5;
// НАКОПЛЕНИЕ СТАТИСТИКИ
while (cnt_events < 1000000) {
// случайный выбор предполагаемой вероятности
// эксперимента, из диапазона 0..1
double probability = get_random_real_0_1();
uint c_true = 0;
for (uint i = 0; i < n; ++i) {
// вероятность события в эксперименте probability,
// и n-раз взяли истина или ложь с выбранной этой вероятностью
bool v = get_true_with_probability(probability);
if (v) ++c_true;
}
// если из n-раз получили k-раз истину, значит это тот самый случай
if (c_true == k) {
uint idx = lrint(floor(probability*sz_ar_events));
assert( idx < sz_ar_events ); // проверка, что с округлением не напутал
++cnt_events; // всего событий
++ar_events[idx]; // событий в этой точке графика
}
}
// ВЫВОД РЕЗУЛЬТАТА
for (uint i = 0; i < sz_ar_events; ++i) {
double p0 = DD(i)/sz_ar_events;
// плотность вероятности:
// вероятность на отрезке деленное на протяженность отрезка
double v = DD(ar_events[i])/cnt_events / (1.0/sz_ar_events);
printf("%4.2f %f\n", p0, v);
}
}Код этой программы можно найти здесь, рядом же вспомогательные функции.
Полученный расчет закинул в эксель и сделал график.

Такой вариант графика можно назвать распределением плотности вероятностей значения вероятности. Его площадь равна единице, которая распределена в этом холмике.
Для полноты картины упомяну, что этот график соответствует графику по формуле Бернулли от параметра вероятность и умноженный на N+1 количества экспериментов.
Далее по тексту, там где в статье употребляю дробь вида k/n, то это не деление, это k событий из n экспериментов, чтобы каждый раз не писать k из n.
Далее. Можно увеличить количество экспериментов, и получить более узкую область расположения основных величин значения вероятность, но как бы их не увеличивали, эта область не сократится до нулевой области с точно известной вероятностью.
На графике ниже изображены распределения для величин 4/5, 7/9, 11/14 и 24/30. Чем уже область, тем выше холмик, площадь которого неизменная единица. Эти соотношения выбраны, потому что они все около 0.8, а не потому что именно такие могут возникнут при 0.8 исходной вероятности. Выбраны, чтобы продемонстрировать, какая область возможных значений остается даже при 30 проведенных экспериментах.
Код программы для этого графика здесь.

Из чего следует, что в действительности экспериментальную вероятность абсолютно точно не определить, а можно лишь предположить область возможного расположения таковой величины, с точностью в зависимости от того сколько произвели замеров.
Сколько бы экспериментов не провели, всегда остается вероятность, что исходная вероятность может оказаться и 0.0001 и 0.9999. Для упрощения крайние маловероятные значения отбрасываются. И берется, скажем, например 95% от основной площади графика распределения.
Такая штука называется доверительные интервалы. Каких-либо рекомендаций, сколько именно и почему процентов нужно оставить я не встречал. Для прогноза погоды берут поменьше, для запуска космических шаттлов побольше. Так же обычно не упоминают, какой все же используется доверительный интервал на вероятность событий и используется ли вообще.
В моей программе расчет границ доверительного интервала осуществляется здесь.
Получилось, что вероятность события определяется плотностью вероятностей значения вероятности, и на это еще нужно наложить процент области основных значений, чтобы можно было хоть что-то определенно сказать, какая все же вероятность у исследуемого события.
Теперь, про более реальный эксперимент.
Пусть будет всем надоевшая монетка, подбрасываем эту монетку, и получаем 4 из 5 выпадений решкой — очень реальный случай. В действительности это не совсем то же самое, что описал чуть выше. Чем это отличается от предыдущего эксперимента?
Предыдущий эксперимент описывался из предположения, что вероятность события может быть равнораспределена на интервале от 0 до 1. В программе это задается строкой double probability = get_random_real_0_1();. Но не бывает монеток с вероятностью выпадения, скажем, 0.1 или 0.9 всегда одной стороной.
Если взять тысячу самых разных монет от обычных до самых кривых, и для каждой произвести замер выпадения путем подбрасывания их по тысяче и более раз, то это покажет, что реально они выпадают одной стороной в диапазоне от 0.4 до 0.6 (это числа навскидку, не буду же я выискивать 1000 монет и каждую подбрасывать 1000 раз).
Как этот факт меняет программу для симуляции вероятностей одной конкретной монеты, для которой получили 4 из 5 выпадения решкой?
Допустим, что распределение выпадения одной стороной для монет описывается как приближение к графику нормального распределения взятого с параметрами средняя = 0.5, стандартное отклонение = 0.1. (на графике ниже он изображен черным цветом).
Когда в программе меняю генерацию исходной вероятности с равнораспределенной на распределенную по указанному правилу, то получаю следующие графики:

Код этого варианта здесь.
Видно, что распределения сильно сдвинулись и теперь определяют несколько иную область, в которой высоковероятно возможна искомая вероятность. Поэтому, если известно, какие вероятности бывают для тех вещей, одну из которых хотим измерить, то это может несколько улучшить результат.
В итоге, 4/5 это ни о чем не говорит и даже 50 проведенных экспериментов не очень информативны. Это очень мало информации, чтобы определить, что за вероятность все же лежит в основе эксперимента.
== Update ==
Как упомянул в комментариях jzha, человек существенно знающий математику, данные графики можно построить и путем точных формул. Но цель данной статьи все же как можно наглядней показать как образуется то, что все в повседневной жизни называют вероятностью.
Для того что бы это строить путем точных формул, это нужно рассмотреть имеющиеся в наличии данные по распределению вероятностей всех монет через аппроксимацию бета распределением, и путем сопряжения распределений выводить уже расчеты. Такая схема это существенный объем по объяснениям, как это сделать, и если я это здесь буду описывать, то это получится скорее статья по математическим расчетам, а не про бытовые вероятности.
Как получить в формулах описанный частный случай с монетой, смотрите комментарии от jzha.