Что такое структура данных?
Проще говоря, структура данных — это контейнер, в котором хранятся данные в определенной компоновке (формате, или способе организации их в памяти). Эта «компоновка» позволяет структуре данных быть эффективной в одних операциях и неэффективной в других. Ваша цель — понять структуры данных, чтобы вы могли выбрать структуру данных, наиболее оптимальную для рассматриваемой проблемы.
Зачем нам нужны структуры данных?
Поскольку структуры данных используются для хранения данных в организованном виде, и поскольку данные являются наиболее важным элементом компьютерной науки, истинная ценность структур данных очевидна.
Независимо от того, какую проблему вы решаете, вам так или иначе приходится иметь дело с данными — будь то зарплата сотрудника, цены на акции, список покупок или даже простой телефонный справочник.
Исходя из разных сценариев, данные должны храниться в определенном формате. У нас есть несколько структур данных, которые покрывают потребность хранить данные в разных форматах.
Обычно используемые структуры данных
Давайте сначала перечислим наиболее часто используемые структуры данных, а затем рассмотрим их одну за другой:
Arrays — Массивы
Массив — это самая простая и наиболее широко используемая структура данных. Другие структуры данных, такие как стеки и очереди, являются производными от массивов.
Вот изображение простого массива размера 4, содержащего элементы (1, 2, 3 и 4).
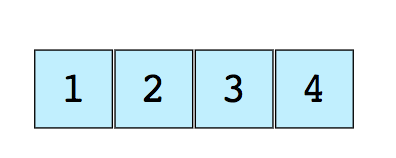
Каждому элементу данных присваивается положительное числовое значение, называемое индексом, которое соответствует позиции этого элемента в массиве. Большинство языков определяют начальный индекс массива как 0.
Ниже приведены два типа массивов:
Основные операции над массивами
Вставить (Insert) — вставляет элемент по указанному индексу
Получить (Get) — возвращает элемент по указанному индексу
Удалить (Delete) — удаляет элемент по указанному индексу
Размер (Size) — получить общее количество элементов в массиве
Для самостоятельного изучения:
1. Найти второй минимальный элемент массива.
2. Первые неповторяющиеся целые числа в массиве.
3. Объединить два отсортированных массива.
4. Переставить положительные и отрицательные значения в массиве.
Stacks (Стеки)
Мы все знакомы со знаменитой опцией Undo (Отмена), которая присутствует практически в каждом приложении. Когда-нибудь задумывались, как это работает? Суть механизма в том, что вы сохраняете предыдущие состояния вашей работы (которые ограничены определенным числом) в памяти в таком порядке, что последнее действие появляется первым. Это не может быть сделано только с помощью массивов. Вот где стек и пригодится!
Реальным примером стека может быть стопка книг, расположенных в вертикальном порядке. Чтобы получить книгу, которая находится где-то посередине, вам нужно удалить все книги, помещенные поверх нее. Вот как работает метод LIFO (Last In First Out).
Вот изображение стека, содержащего три элемента данных (1, 2 и 3), где 3 вверху и будет удалено первым:

Основные операции со стеками:
Протолкнуть (Push) — вставляет элемент сверху других.
Вытащить (Pop) — возвращает верхний элемент после удаления из стека.
Пустой? (IsEmpty) — возвращает истина (true), если стек пуст.
Верхний (Top) — возвращает верхний элемент без удаления из стека.
Для самостоятельного изучения:
1. Оцените постфиксное выражение, используя стек.
2. Сортировка значений в стеке.
3. Проверьте сбалансированные скобки в выражении.
Queues (Очереди)
Подобно стеку, очередь — это еще одна линейная структура данных, в которой элементы хранятся последовательно. Единственное существенное различие между стеком и очередью состоит в том, что вместо использования метода LIFO в Queue реализован метод FIFO, который является сокращением от First in First Out.
Прекрасный реальный пример очереди: ряд людей, ожидающих у билетной кассы. Если приходит новый человек, он присоединяется к линии с конца, а не с начала — и человек, стоящий впереди, первым получит билет и, следовательно, покинет линию.
Вот изображение очереди, содержащей четыре элемента данных (1, 2, 3 и 4), где 1 находится вверху и будет удалено первым:

Основные операции с очередью:
Вочередить (Enqueue) — вставляет элемент в конец очереди.
Выочередить (Dequeue) — удаляет элемент из начала очереди.
Пустой? (IsEmpty) — возвращает истина (true), если очередь пуста.
Верхний (Top) — возвращает первый элемент очереди.
Для самостоятельного изучения:
1. Реализация стека с использованием очереди.
2. Обратные первые k элементы очереди.
3. Генерация двоичных чисел от 1 до n с использованием очереди.
Связанный список (Linked List)
Связанный список — это еще одна важная линейная структура данных, которая на первый взгляд может выглядеть аналогично массивам, но отличается распределением памяти, внутренней структурой и тем, как выполняются основные операции вставки и удаления.
Связанный список подобен цепочке узлов, где каждый узел содержит такую информацию, как данные, и указатель на последующий узел в цепочке. Есть указатель заголовка, который указывает на первый элемент связанного списка, и если список пуст, то он просто указывает на ноль или ничего.
Связанные списки используются для реализации файловых систем, хеш-таблиц и списков смежности.
Вот визуальное представление внутренней структуры связанного списка:

Ниже приведены типы связанных списков:
Основные операции над связанным списком
ВставитьВКонец (InsertAtEnd) — вставляет элемент в конец связанного списка.
ВставитьВНачало (InsertAtHead) — вставляет элемент в начало связанного списка.
Удалить (Delete) — удаляет данный элемент из связанного списка.
УдалитьВНачале (DeleteAtHead) — удаляет первый элемент связанного списка.
Search (Поиск) — возвращает найденный элемент из связанного списка.
Пустой? (IsEmpty) — возвращает истина (true), если связанный список пуст.
Для самостоятельного изучения:
1. Перевернуть связанный список (Обратить, реверсировать, отобразить задом наперёд).
2. Определить цикл в связанном списке.
3. Вернуть N-й узел с конца в связанном списке.
4. Удалить дубликаты из связанного списка.
Graphs (Графы)
Графы — это набор узлов, которые связаны друг с другом в форме сети. Узлы также называются вершинами. Пара (x, y) называется ребром, что указывает на то, что вершина x связана с вершиной y. Ребро может содержать вес / стоимость, показывая, сколько затрат требуется для перехода от вершины x к y.
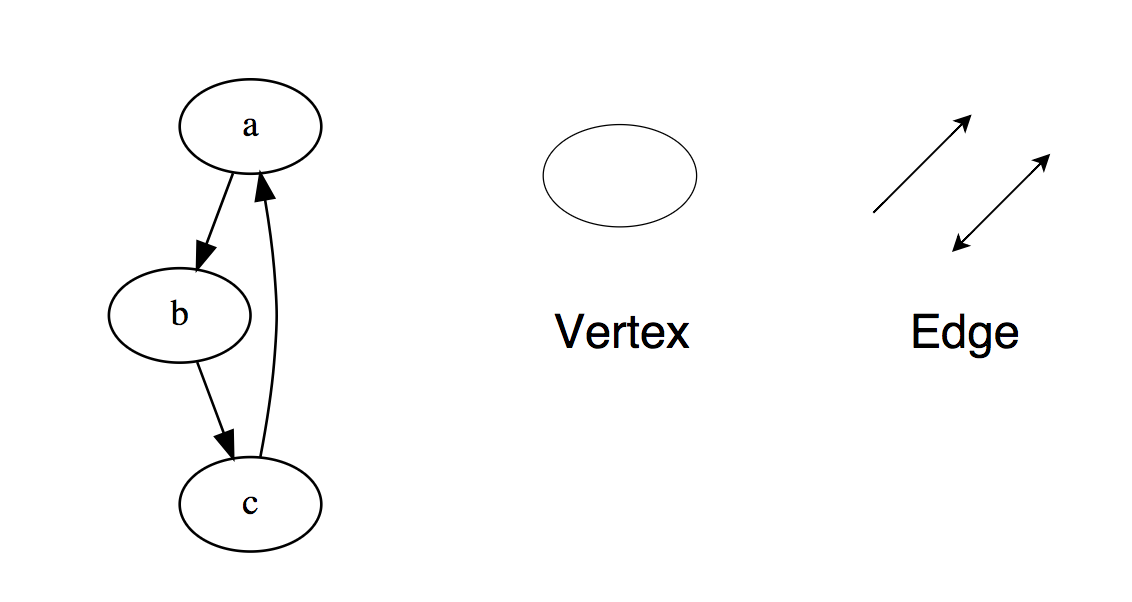
Типы графов:
В языках программирования графы представлены двумя формами:
Ниже приведен пример смежного списка Adjacency List (ненаправленный граф).
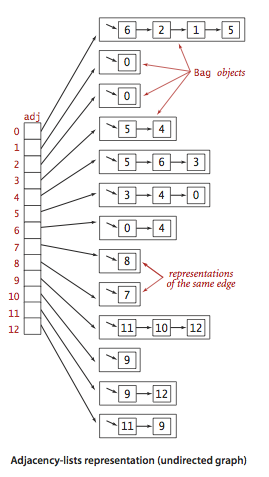
Известные примеры перемещения алгоритмы по графам:
Для самостоятельного изучения:
1. Реализация Breadth and Depth First поиска
2. Проверка если граф дерево или нет.
3. Подсчет количества ребер в графе.
4. Найти кратчайший путь между вершинами.
Trees (Деревья)
Дерево — это иерархическая структура данных, состоящая из вершин (узлов) и ребер, которые их соединяют. Деревья похожи на графы, но ключевой момент, который отличает дерево от графа, состоит в том, что цикл не может существовать в дереве. Дерево — это разорваный граф.
Деревья широко используются в искусственном интеллекте и сложных алгоритмах, чтобы обеспечить эффективный механизм хранения для алгоритмов решения проблемы.
Вот изображение простого дерева и основные термины, используемые в древовидной структуре данных:
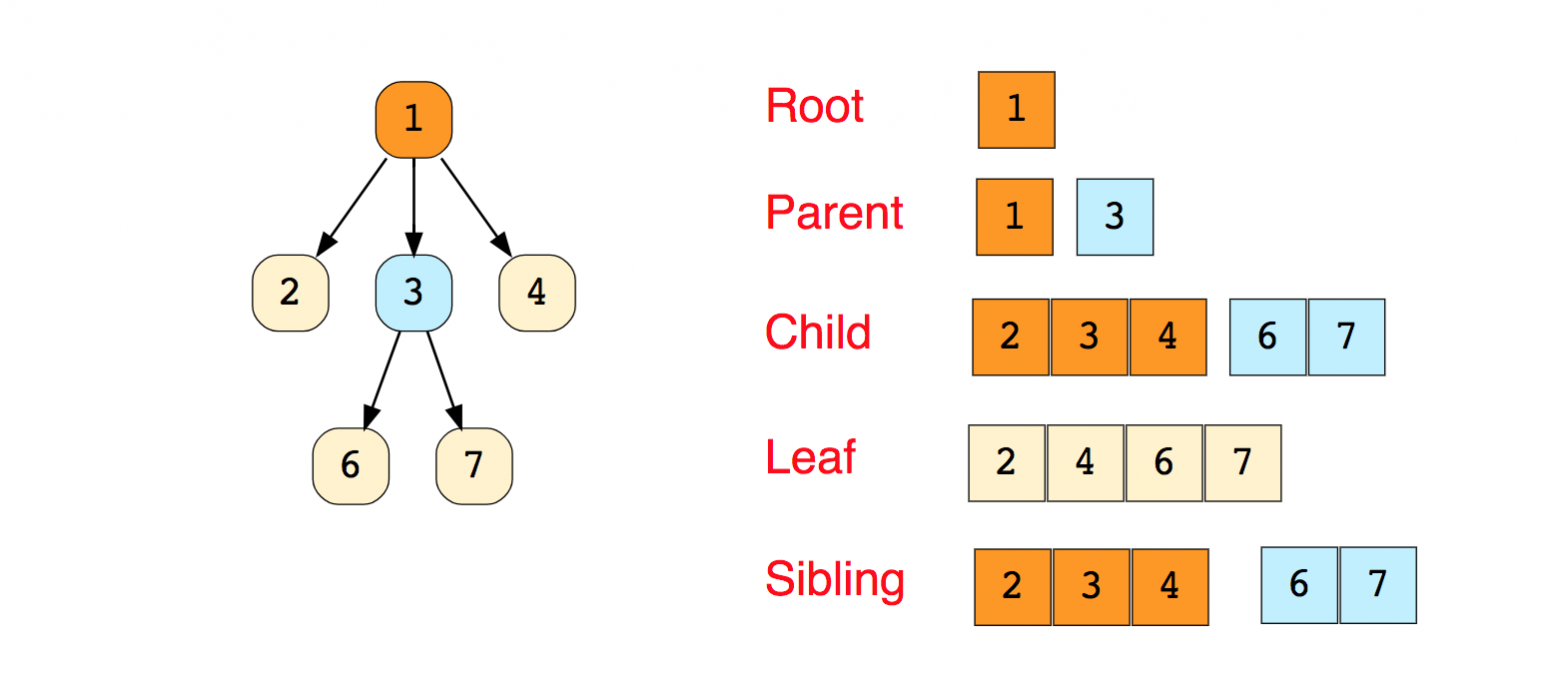
Имеются типы деревьев:
Из вышеперечисленного Бинарное дерево и Бинарное поисковое дерево являются наиболее часто используемыми деревьями.
Для самостоятельного изучения:
1. Найти высоту бинарного дерева.
2. Найти k-е максимальное значение в двоичном поисковом дереве.
3. Найти узлы на расстоянии «k» от корня.
4. Найти предков данного узла в двоичном дереве.
Практические примеры:
1. Facebook: Каждый пользователь представляет собой вершину, и два человека являются друзьями, когда имеется ребро между двумя вершинами. Так же и рекомендации в друзья — расчитываются на основаниитеории графов.
2. Карты Google: Различные локации представлены вершинами и дороги представлены ребрами, теория графов используется для нахождения кратчайшего пути между двумя вершинами.
3. Транспортные сети: в них вершины это пересечения дорог и рёбра — это дорожные сегменты между их пересечениями.
4. Представление молекулярных структур где вершины это молекулы и рёбра — это связи между молекулами.
5. Дискретные сигнальные процессы в графах. (и тут еще хорошая статья ну и заодно вот эта)
6. Эмпирические наблюдения показывают, что большинство генов регулируются небольшим количеством других генов, обычно менее десяти. Следовательно, генетическая сеть может рассматриваться как разреженный граф, то есть граф, в котором узел связан с несколькими другими узлами. Если ориентированные (ациклические) графы или неориентированные графы насыщены вероятностями, то результатом являются вероятностно ориентированные графические модели и вероятностные неориентированные графические модели соответственно.
7. Теория расширение кластера Майера функции летучести газа (Z) в термодинамике требует вычисления двух, трех, четырёх условий и так далее. Существует систематический способ сделать это комбинаторно с диаграммами, и это помогает узнать связность таких диаграмм. Знание теории графов может быть полезным, когда вы хотите суммировать подмножество этих диаграмм.
8. Раскраска карты: знаменитая теорема о четырех цветах утверждает, что всегда можно правильно раскрасить регионы карты так, чтобы никаким двум смежным регионам не был назначен один и тот же цвет, используя не более четырех разных цветов. В этой модели регионы с цветами — это узлы, а смежность — ребра графа.
9. Задача с тремя коттеджами — это хорошо известная математическая головоломка. Ее можно сформулировать так: Три коттеджа на плоскости (или сфере), каждый из которых должен быть подключен к газовым, водопроводным и электрическим компаниям. Задача решается при помощи графа на плоскости.
10. Поиск центра графа: Для каждой вершины найдите длину кратчайшего пути к самой дальней вершине. Центром графа является вершина, для которой это значение минимально. Это важно для архитектурного планирования населенных пунктов, в которых больница, пожарная служба или отделение полиции должны быть расположены в так, чтобы самая дальняя точка была как можно ближе.
Для любителей С#, как я, линк с примерами кода построения графов на C# тут. Для самых продвинутых библиотека с реализацией графов на C++ тут. Для фанатов AI и Skynet топать сюда.
Очередности (Trie)
Очередности, также известные как деревья с префиксами (Prefix Trees), представляют собой древовидную структуру данных, которая оказывается достаточно эффективной для решения проблем, связанных со строками. Они обеспечивают быстрый поиск и, в основном, используются для поиска слов в словаре, автоматического предложения в поисковой системе и даже для IP-маршрутизации.
Вот иллюстрация того, как три слова «top», «thus», и «their» хранятся в Очередности:

Слова хранятся сверху вниз, где зеленые узлы “p”, “s” и “r” указывают на конец “top”, “thus”, и “their” соответственно.
Для самостоятельного изучения:
1. Подсчитать общее количество слов в Очередности.
2. Распечатать все слова, хранящиеся в Очередности.
3. Сортировка элементов массива с использованием Очередности.
4. Формируйте слова из словаря, используя Очередности.
5. Создайте словарь T9.
Практические примеры использования:
1. Выбор из словаря или завершение при наборе слова.
2. Поиск в контактах в телефоне или телефонном словаре.
Hash Table (Хеш-таблица)
Хеширование — это процесс, используемый для уникальной идентификации объектов и сохранения каждого объекта по некоторому предварительно рассчитанному уникальному индексу, называемому его «ключом». Таким образом, объект хранится в форме пары «ключ-значение», а коллекция таких элементов называется «словарь». Каждый объект может быть найден с помощью этого ключа.
Существуют разные структуры данных, основанные на хешировании, но наиболее часто используемой структурой данных является хеш-таблица. Хэш-таблица используется, когда вам нужно получить доступ к элементам с помощью ключа, и вы можете определить полезное значение ключа.
Хеш-таблицы обычно реализуются с использованием массивов.
Производительность хеширования структуры данных зависит от этих трех факторов:
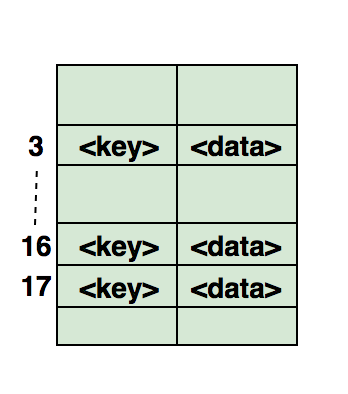
Вот иллюстрация того, как хэш отображается в массиве. Индекс этого массива вычисляется с помощью хэш-функции.
Для самостоятельного изучения:
1. Найти симметричные пары в массиве.
2. Проследить полный путь путешествия.
3. Найти, если массив является подмножеством другого массива.
4. Проверьте, являются ли данные массивы непересекающимися.
Ниже приведен пример кода использования хэш-таблицы в .Net
Практические примеры:
1. Игра «Жизнь». В ней хэш — это набор координат каждой живой клетки.
2. Примитивный вариант поисковой системы Google мог бы картировать все существующие слова в набор URL где они встречаются. В этом случае, хэштаблицы используются дважды: в первый раз для картирования слов в наборы URLs, и, во второй раз, для сохранения каждого набора URLs.
3. При имплементации структуры/алгоритма многонаправленного дерева (multiway tree) хэштаблицы могут использоваться для быстрого доступа к любому дочернему элементу внутреннего узла.
4. При написании программы для игры в шахматы, очень важно отслеживать позиции оцененные ранее, так что можно было бы вернуться, когда понадобится к ним снова при необходимости.
5. Любой язык программирования нуждается в картировании имени переменной ее адресу в памяти. Фактически, в скриптовых языках как Javascript и Perl, поля могут быть добавлены в объекту динамически, это означает, что объекты сами по себе как хэш-карты.
Проще говоря, структура данных — это контейнер, в котором хранятся данные в определенной компоновке (формате, или способе организации их в памяти). Эта «компоновка» позволяет структуре данных быть эффективной в одних операциях и неэффективной в других. Ваша цель — понять структуры данных, чтобы вы могли выбрать структуру данных, наиболее оптимальную для рассматриваемой проблемы.
Зачем нам нужны структуры данных?
Поскольку структуры данных используются для хранения данных в организованном виде, и поскольку данные являются наиболее важным элементом компьютерной науки, истинная ценность структур данных очевидна.
Независимо от того, какую проблему вы решаете, вам так или иначе приходится иметь дело с данными — будь то зарплата сотрудника, цены на акции, список покупок или даже простой телефонный справочник.
Исходя из разных сценариев, данные должны храниться в определенном формате. У нас есть несколько структур данных, которые покрывают потребность хранить данные в разных форматах.
Обычно используемые структуры данных
Давайте сначала перечислим наиболее часто используемые структуры данных, а затем рассмотрим их одну за другой:
- Arrays — массивы
- Stacks — стеки
- Queues — очереди
- Linked Lists — связанные списки
- Trees — деревья
- Graphs — графы
- Tries (они, по сути, деревья, но все же хорошо называть их отдельно). — очередности
- Hash Tables — хэш таблицы
Arrays — Массивы
Массив — это самая простая и наиболее широко используемая структура данных. Другие структуры данных, такие как стеки и очереди, являются производными от массивов.
Вот изображение простого массива размера 4, содержащего элементы (1, 2, 3 и 4).

Каждому элементу данных присваивается положительное числовое значение, называемое индексом, которое соответствует позиции этого элемента в массиве. Большинство языков определяют начальный индекс массива как 0.
Ниже приведены два типа массивов:
- Одномерные массивы (как показано выше) One-dimensional arrays
- Многомерные массивы (массивы внутри массивов) Multi-dimensional arrays
Основные операции над массивами
Вставить (Insert) — вставляет элемент по указанному индексу
Получить (Get) — возвращает элемент по указанному индексу
Удалить (Delete) — удаляет элемент по указанному индексу
Размер (Size) — получить общее количество элементов в массиве
Для самостоятельного изучения:
1. Найти второй минимальный элемент массива.
2. Первые неповторяющиеся целые числа в массиве.
3. Объединить два отсортированных массива.
4. Переставить положительные и отрицательные значения в массиве.
Stacks (Стеки)
Мы все знакомы со знаменитой опцией Undo (Отмена), которая присутствует практически в каждом приложении. Когда-нибудь задумывались, как это работает? Суть механизма в том, что вы сохраняете предыдущие состояния вашей работы (которые ограничены определенным числом) в памяти в таком порядке, что последнее действие появляется первым. Это не может быть сделано только с помощью массивов. Вот где стек и пригодится!
Реальным примером стека может быть стопка книг, расположенных в вертикальном порядке. Чтобы получить книгу, которая находится где-то посередине, вам нужно удалить все книги, помещенные поверх нее. Вот как работает метод LIFO (Last In First Out).
Вот изображение стека, содержащего три элемента данных (1, 2 и 3), где 3 вверху и будет удалено первым:

Основные операции со стеками:
Протолкнуть (Push) — вставляет элемент сверху других.
Вытащить (Pop) — возвращает верхний элемент после удаления из стека.
Пустой? (IsEmpty) — возвращает истина (true), если стек пуст.
Верхний (Top) — возвращает верхний элемент без удаления из стека.
Для самостоятельного изучения:
1. Оцените постфиксное выражение, используя стек.
2. Сортировка значений в стеке.
3. Проверьте сбалансированные скобки в выражении.
Queues (Очереди)
Подобно стеку, очередь — это еще одна линейная структура данных, в которой элементы хранятся последовательно. Единственное существенное различие между стеком и очередью состоит в том, что вместо использования метода LIFO в Queue реализован метод FIFO, который является сокращением от First in First Out.
Прекрасный реальный пример очереди: ряд людей, ожидающих у билетной кассы. Если приходит новый человек, он присоединяется к линии с конца, а не с начала — и человек, стоящий впереди, первым получит билет и, следовательно, покинет линию.
Вот изображение очереди, содержащей четыре элемента данных (1, 2, 3 и 4), где 1 находится вверху и будет удалено первым:

Основные операции с очередью:
Вочередить (Enqueue) — вставляет элемент в конец очереди.
Выочередить (Dequeue) — удаляет элемент из начала очереди.
Пустой? (IsEmpty) — возвращает истина (true), если очередь пуста.
Верхний (Top) — возвращает первый элемент очереди.
Для самостоятельного изучения:
1. Реализация стека с использованием очереди.
2. Обратные первые k элементы очереди.
3. Генерация двоичных чисел от 1 до n с использованием очереди.
Связанный список (Linked List)
Связанный список — это еще одна важная линейная структура данных, которая на первый взгляд может выглядеть аналогично массивам, но отличается распределением памяти, внутренней структурой и тем, как выполняются основные операции вставки и удаления.
Связанный список подобен цепочке узлов, где каждый узел содержит такую информацию, как данные, и указатель на последующий узел в цепочке. Есть указатель заголовка, который указывает на первый элемент связанного списка, и если список пуст, то он просто указывает на ноль или ничего.
Связанные списки используются для реализации файловых систем, хеш-таблиц и списков смежности.
Вот визуальное представление внутренней структуры связанного списка:

Ниже приведены типы связанных списков:
- Односвязный список (однонаправленный)
- Двусвязный список (двунаправленный)
Основные операции над связанным списком
ВставитьВКонец (InsertAtEnd) — вставляет элемент в конец связанного списка.
ВставитьВНачало (InsertAtHead) — вставляет элемент в начало связанного списка.
Удалить (Delete) — удаляет данный элемент из связанного списка.
УдалитьВНачале (DeleteAtHead) — удаляет первый элемент связанного списка.
Search (Поиск) — возвращает найденный элемент из связанного списка.
Пустой? (IsEmpty) — возвращает истина (true), если связанный список пуст.
Для самостоятельного изучения:
1. Перевернуть связанный список (Обратить, реверсировать, отобразить задом наперёд).
2. Определить цикл в связанном списке.
3. Вернуть N-й узел с конца в связанном списке.
4. Удалить дубликаты из связанного списка.
Graphs (Графы)
Графы — это набор узлов, которые связаны друг с другом в форме сети. Узлы также называются вершинами. Пара (x, y) называется ребром, что указывает на то, что вершина x связана с вершиной y. Ребро может содержать вес / стоимость, показывая, сколько затрат требуется для перехода от вершины x к y.

Типы графов:
- Undirected Graph
- Directed Graph
В языках программирования графы представлены двумя формами:
Ниже приведен пример смежного списка Adjacency List (ненаправленный граф).

Известные примеры перемещения алгоритмы по графам:
Для самостоятельного изучения:
1. Реализация Breadth and Depth First поиска
2. Проверка если граф дерево или нет.
3. Подсчет количества ребер в графе.
4. Найти кратчайший путь между вершинами.
Trees (Деревья)
Дерево — это иерархическая структура данных, состоящая из вершин (узлов) и ребер, которые их соединяют. Деревья похожи на графы, но ключевой момент, который отличает дерево от графа, состоит в том, что цикл не может существовать в дереве. Дерево — это разорваный граф.
Деревья широко используются в искусственном интеллекте и сложных алгоритмах, чтобы обеспечить эффективный механизм хранения для алгоритмов решения проблемы.
Вот изображение простого дерева и основные термины, используемые в древовидной структуре данных:

Имеются типы деревьев:
- N-ое дерево
- Сбалансированное дерево (Balanced Tree)
- Бинарное дерево (Binary Tree)
- Бинарное поисковое дерево (Binary Search Tree)
- AVL дерево
- Красно-черное дерево (Red Black Tree)
- 2–3 дерево
Из вышеперечисленного Бинарное дерево и Бинарное поисковое дерево являются наиболее часто используемыми деревьями.
Для самостоятельного изучения:
1. Найти высоту бинарного дерева.
2. Найти k-е максимальное значение в двоичном поисковом дереве.
3. Найти узлы на расстоянии «k» от корня.
4. Найти предков данного узла в двоичном дереве.
Практические примеры:
1. Facebook: Каждый пользователь представляет собой вершину, и два человека являются друзьями, когда имеется ребро между двумя вершинами. Так же и рекомендации в друзья — расчитываются на основаниитеории графов.
2. Карты Google: Различные локации представлены вершинами и дороги представлены ребрами, теория графов используется для нахождения кратчайшего пути между двумя вершинами.
3. Транспортные сети: в них вершины это пересечения дорог и рёбра — это дорожные сегменты между их пересечениями.
4. Представление молекулярных структур где вершины это молекулы и рёбра — это связи между молекулами.
5. Дискретные сигнальные процессы в графах. (и тут еще хорошая статья ну и заодно вот эта)
6. Эмпирические наблюдения показывают, что большинство генов регулируются небольшим количеством других генов, обычно менее десяти. Следовательно, генетическая сеть может рассматриваться как разреженный граф, то есть граф, в котором узел связан с несколькими другими узлами. Если ориентированные (ациклические) графы или неориентированные графы насыщены вероятностями, то результатом являются вероятностно ориентированные графические модели и вероятностные неориентированные графические модели соответственно.
7. Теория расширение кластера Майера функции летучести газа (Z) в термодинамике требует вычисления двух, трех, четырёх условий и так далее. Существует систематический способ сделать это комбинаторно с диаграммами, и это помогает узнать связность таких диаграмм. Знание теории графов может быть полезным, когда вы хотите суммировать подмножество этих диаграмм.
8. Раскраска карты: знаменитая теорема о четырех цветах утверждает, что всегда можно правильно раскрасить регионы карты так, чтобы никаким двум смежным регионам не был назначен один и тот же цвет, используя не более четырех разных цветов. В этой модели регионы с цветами — это узлы, а смежность — ребра графа.
9. Задача с тремя коттеджами — это хорошо известная математическая головоломка. Ее можно сформулировать так: Три коттеджа на плоскости (или сфере), каждый из которых должен быть подключен к газовым, водопроводным и электрическим компаниям. Задача решается при помощи графа на плоскости.
10. Поиск центра графа: Для каждой вершины найдите длину кратчайшего пути к самой дальней вершине. Центром графа является вершина, для которой это значение минимально. Это важно для архитектурного планирования населенных пунктов, в которых больница, пожарная служба или отделение полиции должны быть расположены в так, чтобы самая дальняя точка была как можно ближе.
Для любителей С#, как я, линк с примерами кода построения графов на C# тут. Для самых продвинутых библиотека с реализацией графов на C++ тут. Для фанатов AI и Skynet топать сюда.
Очередности (Trie)
Очередности, также известные как деревья с префиксами (Prefix Trees), представляют собой древовидную структуру данных, которая оказывается достаточно эффективной для решения проблем, связанных со строками. Они обеспечивают быстрый поиск и, в основном, используются для поиска слов в словаре, автоматического предложения в поисковой системе и даже для IP-маршрутизации.
Вот иллюстрация того, как три слова «top», «thus», и «their» хранятся в Очередности:

Слова хранятся сверху вниз, где зеленые узлы “p”, “s” и “r” указывают на конец “top”, “thus”, и “their” соответственно.
Для самостоятельного изучения:
1. Подсчитать общее количество слов в Очередности.
2. Распечатать все слова, хранящиеся в Очередности.
3. Сортировка элементов массива с использованием Очередности.
4. Формируйте слова из словаря, используя Очередности.
5. Создайте словарь T9.
Практические примеры использования:
1. Выбор из словаря или завершение при наборе слова.
2. Поиск в контактах в телефоне или телефонном словаре.
Hash Table (Хеш-таблица)
Хеширование — это процесс, используемый для уникальной идентификации объектов и сохранения каждого объекта по некоторому предварительно рассчитанному уникальному индексу, называемому его «ключом». Таким образом, объект хранится в форме пары «ключ-значение», а коллекция таких элементов называется «словарь». Каждый объект может быть найден с помощью этого ключа.
Существуют разные структуры данных, основанные на хешировании, но наиболее часто используемой структурой данных является хеш-таблица. Хэш-таблица используется, когда вам нужно получить доступ к элементам с помощью ключа, и вы можете определить полезное значение ключа.
Хеш-таблицы обычно реализуются с использованием массивов.
Производительность хеширования структуры данных зависит от этих трех факторов:
- Хэш-функция
- Размер хеш-таблицы
- Метод обработки столкновений
Вот иллюстрация того, как хэш отображается в массиве. Индекс этого массива вычисляется с помощью хэш-функции.

Для самостоятельного изучения:
1. Найти симметричные пары в массиве.
2. Проследить полный путь путешествия.
3. Найти, если массив является подмножеством другого массива.
4. Проверьте, являются ли данные массивы непересекающимися.
Ниже приведен пример кода использования хэш-таблицы в .Net
static void Main(string[] args) { Hashtable ht = new Hashtable { { "001", "Zara Ali" }, { "002", "Abida Rehman" }, { "003", "Joe Holzner" }, { "004", "Mausam Benazir Nur" }, { "005", "M. Amlan" }, { "006", "M. Arif" }, { "007", "Ritesh Saikia" } }; if (ht.ContainsValue("Nuha Ali")) { Console.WriteLine("Эта персона уже в списке!"); } else { ht.Add("008", "Nuha Ali"); } // Получить коллекцию ключей. ICollection key = ht.Keys; foreach (string k in key) { Console.WriteLine(k + ": " + ht[k]); } Console.ReadKey(); }
Практические примеры:
1. Игра «Жизнь». В ней хэш — это набор координат каждой живой клетки.
2. Примитивный вариант поисковой системы Google мог бы картировать все существующие слова в набор URL где они встречаются. В этом случае, хэштаблицы используются дважды: в первый раз для картирования слов в наборы URLs, и, во второй раз, для сохранения каждого набора URLs.
3. При имплементации структуры/алгоритма многонаправленного дерева (multiway tree) хэштаблицы могут использоваться для быстрого доступа к любому дочернему элементу внутреннего узла.
4. При написании программы для игры в шахматы, очень важно отслеживать позиции оцененные ранее, так что можно было бы вернуться, когда понадобится к ним снова при необходимости.
5. Любой язык программирования нуждается в картировании имени переменной ее адресу в памяти. Фактически, в скриптовых языках как Javascript и Perl, поля могут быть добавлены в объекту динамически, это означает, что объекты сами по себе как хэш-карты.
