MarkWatney 23 мар 2021 в 13:33

Свой AR. Маркеры

11 мин

4.1K

AR и VRАлгоритмы*Математика*Разработка под AR и VR*

Туториал

Привет, Хабр.

По мере написания библиотеки в этой статье я хочу продолжить объяснять математику, лежащей в основе работы дополненной реальности. Результатом будет пример на игровом движке Unity, распознающий маркер и накладывающий на него трехмерную модельку. Библиотека пишется на C++ под Android, но фокус статьи будет направлен на математику. Эта статья, в отличии от предыдущей, будет ближе к практике, но если необходимо разобраться с основами векторной математики, то можно начать с нее.

Однородные координаты

В предыдущей статье мы рассматривали преобразования в евклидовом пространстве — $\mathbb{R}^2$ , а сейчас ведем понятие проективного пространства — $\mathbb{P}^2$ (projective space).

Чтобы перевести координаты точки из двумерного евклидова пространства в проективное, нужно умножить вектор координат на любой ненулевой скаляр $inline$ , а затем добавить $inline$ в качестве последней компоненты: $\vec v = \begin{pmatrix} x & y \end{pmatrix}^T \in \mathbb{R}^2 \space \Rightarrow \space \vec p = \begin{pmatrix} x \cdot w & y \cdot w & w \end{pmatrix}^T \in \mathbb{P}^2$ . Получаем однородные координаты точки (homogeneous coordinates). Так как $inline$ — свободная переменная, то одной точке евклидова пространства принадлежит бесконечное множество точек проективного пространства. Перевод обратно выполняется делением на последнюю компоненту: $\vec p = \begin{pmatrix} x & y & w \end{pmatrix}^T \in \mathbb{P}^2 \space \Rightarrow \space \vec v = \begin{pmatrix} \frac{x}{w} & \frac{y}{w} \end{pmatrix}^T \in \mathbb{R}^2$ . Удобно в качестве значения $inline$ брать 1: $\vec v = \begin{pmatrix} x & y \end{pmatrix}^T \in \mathbb{R}^2 \space \Rightarrow \space \vec p = \begin{pmatrix} x & y & 1 \end{pmatrix}^T \in \mathbb{P}^2$ . Перевод обратно в таком случае также упрощается: $\vec p = \begin{pmatrix} x & y & 1 \end{pmatrix}^T \in \mathbb{P}^2 \space \Rightarrow \space \vec v = \begin{pmatrix} x & y \end{pmatrix}^T \in \mathbb{R}^2$ .

Можно заметить, что умножение однородных координат на скаляр не меняет координат соответствующей точки в евклидовом пространстве: $\vec{p_B} = \vec{p_A} \cdot s = \begin{pmatrix} x \cdot s & y \cdot s & w \cdot s \end{pmatrix}^T \in \mathbb{P}^2 \space \Rightarrow \space \vec v = \begin{pmatrix} \frac{x \cdot s}{w \cdot s} & \frac{y \cdot s}{w \cdot s} \end{pmatrix}^T = \begin{pmatrix} \frac{x}{w} & \frac{y}{w} \end{pmatrix}^T \in \mathbb{R}^2$ .

Также, если последняя компонента равна 0, то такую точку мы не сможем перевести в евклидово пространство: $\vec p = \begin{pmatrix} x & y & 0 \end{pmatrix}^T \in \mathbb{P}^2$ – такая точка называется точкой на бесконечности (point at infinity или ideal point).

Трансформации в однородных координатах

Трансформации, которые мы делали в евклидовом пространстве, можно применять и для однородных координат.

Для примера возьмем поворот точек матрицей поворота: $\vec{v'} = R \vec{v} = \begin{pmatrix} R_{11} & R_{12} \\ R_{21} & R_{22} \end{pmatrix} \begin{pmatrix} v_x \\ v_y \end{pmatrix} = \begin{pmatrix} {v'}_x \\ {v'}_y \end{pmatrix}$ .
В однородных координатах это принимает такую форму: $\vec{v'} = R \vec{v} = \begin{pmatrix} R_{11} & R_{12} & 0 \\ R_{21} & R_{22} & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} v_x \\ v_y \\ 1 \end{pmatrix} = \begin{pmatrix} {v'}_x \\ {v'}_y \\ 1 \end{pmatrix}$

А смещение выполнялось следующим образом: $\vec{v'} = \vec v + \vec t$ . Мы не могли преобразовать смещение объекта в матричную операцию, так как она нелинейна в евклидовом пространстве. Но уже в проективном пространстве она становится линейной $inline$ : $\vec{v'} = \begin{pmatrix} 0 & 0 & t_x \\ 0 & 0 & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} v_x & v_y & 1 \end{pmatrix} = \begin{pmatrix} v_x + t_x \\ v_y + t_y \\ 1 \end{pmatrix}$ .

Из предыдущей статьи мы помним, что матричные операции, можно объединять. Объединим поворот и смещение:
$\vec{v'} = T \cdot R \cdot \vec v = \begin{pmatrix} 0 & 0 & t_x \\ 0 & 0 & t_y \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} R_{11} & R_{12} & 0 \\ R_{21} & R_{22} & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} v_x \\ v_y \\ 1 \end{pmatrix}$

$\vec{v'} = \begin{pmatrix} R_{11} & R_{12} & t_x \\ R_{21} & R_{22} & t_y \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} v_x \\ v_y \\ 1 \end{pmatrix}$

Метод наименьших квадратов

Прежде чем двигаться дальше, вооружимся новым инструментом — методом наименьших квадратов (МНК).

Возьмем для примера такую систему линейных уравнений:
$\begin{cases} A_{11} \cdot x_1 + A_{12} \cdot x_2 = b_1 \\ A_{21} \cdot x_1 + A_{22} \cdot x_2 = b_2 \\ A_{31} \cdot x_1 + A_{32} \cdot x_1 = b_3\end{cases}$
Эту систему можно представить в матричном виде:
$\begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \\ A_{31} & A_{32} \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} = A \cdot \vec{x} = \vec{b}$ .

Неизвестных у нас два, количество уравнений — три, значит это переопределенная система уравнений. А значит решения одних уравнений может противоречить другим, и система может не иметь точного решения. Ошибка получаемых решений — это обычное дело для вычислительной математики, нужно только ее минимизировать. В качестве ошибки возьмем сумму квадратов разницы: пусть $\vec{b'} = A \cdot \vec{x}$ , $\vec{r} = (\vec{b'} - \vec{b})$ — вектор остатков, $e(\vec{x}) = \sum{{r_i}^2} = \sum{({b'}_i - b_i)^2}$ — функция ошибки. $e(\vec{x}) \rightarrow min$ .
В матричном виде задачу минимизации можно записать так: $(A \vec x - \vec b)^T (A \vec x - \vec b) \rightarrow min$ .

Решение нашей системы:
$A \cdot \vec x = \vec b \space \Rightarrow \space A^T \cdot A \cdot \vec x = A^T \vec b \space \Rightarrow \space \vec x = (A^T \cdot A)^{-1} \cdot A^T \cdot \vec b$
$\vec x = (A^T A)^{-1} A^T \vec b$
Метод можно применять и для системы нелинейных уравнений. Мы определили функцию ошибки как сумму квадратов остатков. Дальше нам нужно найти минимум этой функции. Минимум функции нужно искать в ее экстремумах. Экстремумы находятся там, где производные функции равны нулю:
$\begin{cases}\frac{\partial e(\vec x)}{\partial x_0} = 0 \\ .. \\ \frac{\partial e(\vec x)}{\partial x_n} = 0 \end{cases}$
Получим систему уравнений, которая в отличии от предыдущей, будет точно не переопределена. Если система уравнений — линейная, то решение будет только одно и получить его не составляет труда. Если решений несколько, то перебираем их и выбираем минимальное.

Немного практики

Перейдем наконец к практическим экспериментам. Для того, чтобы упростить себе работу, возьмем пока библиотеку OpenCV и используем ее для поиска маркеров. Найдем маркер и наложим на него изображение.

Пусть $inline$ и $inline$ — ширина и высота накладываемого изображения. Тогда четыре угла будут иметь следующие локальные координаты:
$[\vec{v_1}, \vec{v_2}, \vec{v_3}, \vec{v_4}] = [\begin{pmatrix} 0 & 0 \end{pmatrix}^T, \begin{pmatrix} w & 0 \end{pmatrix}^T, \begin{pmatrix} w & h \end{pmatrix}^T, \begin{pmatrix} 0 & h \end{pmatrix}^T]$
От OpenCV мы получаем координаты 4х углов маркера в кадре: $[\vec{m_1}, \vec{m_2}, \vec{m_3}, \vec{m_4}]$

Для наложении изображения на маркер нам необходимо описать преобразование из локальных координат накладываемого изображения в координаты кадра с камеры. Для этого возьмем два вектора $\vec{aX}$ и $\vec{aY}$ , описывающих базовые оси $inline$ , $inline$ и вектор смещения от начала координат — $\vec{t}$ :
$\begin{pmatrix} {{m'}_i}_x \\ {{m'}_i}_y \\ 1 \end{pmatrix} = \begin{pmatrix} aX_x & aY_x & t_x \\ aX_y & aY_y & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} {v_i}_x \\ {v_i}_y \\ 1 \end{pmatrix}$
Можем упростить формулу, вычеркнув последнюю строку:
$\begin{pmatrix} {{m'}_i}_x \\ {{m'}_i}_y \end{pmatrix} = \begin{pmatrix} aX_x & aY_x & t_x \\ aX_y & aY_y & t_y \end{pmatrix} \begin{pmatrix} {v_i}_x \\ {v_i}_y \end{pmatrix}$
$\vec{{m'}_i} = \begin{pmatrix} \vec{aX} & \vec{aY} & \vec t \end{pmatrix} \vec{v_i}$
Одна пара точек задает два линейных уравнений, при этом имеем 6 неизвестных. Значит нужно 3 пары точек, чтобы система была определена. Мы имеем 4, а значит она переопределена. Воспользуемся МНК для нахождения нашего преобразования:

Пусть искомый вектор $\vec x$ будет собран из наших неизвестных следующим образом $\vec x = \begin{pmatrix} aX_x & aY_x & t_x & aX_y & aY_y & t_y \end{pmatrix}^T$ .

Исходя из такого вектора $\vec x$ , матрица $inline$ , задающая нашу линейную систему уравнений будет иметь следующий вид:
$A = \begin{pmatrix} {v_1}_x & {v_1}_y & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & {v_1}_x & {v_1}_y & 1 \\ ... \\ {v_4}_x & {v_4}_y & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & {v_4}_x & {v_4}_y & 1 \end{pmatrix}$
А вектор $\vec b$ будет равен:
$\vec b = \begin{pmatrix} {m_1}_x \\ {m_1}_y \\ ... \\ {m_4}_x \\ {m_4}_y \end{pmatrix}$
Тогда, используя МНК, можем получить решение нашей системы: $\vec x = (A^T A)^{-1} A^T \vec b$ . Отсюда получаем $\vec{aX}$ , $\vec{aY}$ и $\vec{t}$ .

Пробуем!

Affine

Красным рисуются координаты маркера, полученного от OpenCV. В целом работает, но если взять низкий угол по отношению к маркеру, то видно, что искажения работают неправильно. А так получилось, потому что для моделирования пространственных искажений маркера мы использовали аффинную матрицу. Важное свойство аффинной матрицы — линии, полученные после преобразования, остаются параллельными. Однако обычно, смотря на параллельные линии на плоскости, мы видим такую картину:

Параллельные линии при проецировании сходятся в одной точке, т.е. становятся не параллельными. Значит аффинной матрицы нам недостаточно.

Direct linear transformation

Получить лучший результат нам поможет алгоритм, который называется Direct linear transformation.

А описать перспективные искажения поможет перспективная матрица размером 3x3: $H = \begin{pmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{pmatrix}$ .

Перевод из евклидовых координат в однородные обозначим как $inline$ и распишем полученное преобразование для наших $inline$ точек ( $inline$ , а $inline$ в нашем случае):
$\vec{p_i} = project(H \cdot \begin{pmatrix} {v_i}_x \\ {v_i}_y \\ 1 \end{pmatrix}) = \begin{pmatrix} \frac{ H_{11} \cdot {v_i}_x + H_{12} \cdot {v_i}_y + H_{13}}{H_{31} \cdot {v_i}_x + H_{32} \cdot {v_i}_y + H_{33}} & \frac{ H_{21} \cdot {v_i}_x + H_{22} \cdot {v_i}_y + H_{23}}{H_{31} \cdot {v_i}_x + H_{32} \cdot {v_i}_y + H_{33}} \end{pmatrix}^T$
Представим наши уравнения в виде системы уравнений:
$\begin{cases} ... \\ {p_i}_x = \frac{ H_{11} \cdot {v_i}_x + H_{12} \cdot {v_i}_y + H_{13}}{H_{31} \cdot {v_i}_x + H_{32} \cdot {v_i}_y + H_{33}} \\ {p_i}_y = \frac{ H_{21} \cdot {v_i}_x + H_{22} \cdot {v_i}_y + H_{23}}{H_{31} \cdot {v_i}_x + H_{32} \cdot {v_i}_y + H_{33}} \\ .. \end{cases}$

$\begin{cases} ... \\ {p_i}_x \cdot (H_{31} \cdot {v_i}_x + H_{32} \cdot {v_i}_y + H_{33}) = H_{11} \cdot {v_i}_x + H_{12} \cdot {v_i}_y + H_{13} \\ {p_i}_y \cdot (H_{31} \cdot {v_i}_x + H_{32} \cdot {v_i}_y + H_{33}) = H_{21} \cdot {v_i}_x + H_{22} \cdot {v_i}_y + H_{23} \\ ... \end{cases}$

$\begin{cases} ... \\ H_{11} \cdot v_x + H_{12} \cdot v_y + H_{13} - H_{31} \cdot v_x \cdot {p_i}_x - H_{32} \cdot v_y \cdot {p_i}_x - H_{33} \cdot {p_i}_x = 0 \\ H_{21} \cdot v_x + H_{22} \cdot v_y + H_{23} - H_{31} \cdot v_x \cdot {p_i}_y - H_{32} \cdot v_y \cdot {p_i}_y - H_{33} \cdot {p_i}_y = 0 \\ ... \end{cases}$

Представим матрицу $inline$ как вектор $\vec{h} = \begin{pmatrix} H_{11} & H_{12} & H_{13} & H_{21} & H_{22} & H_{23} & H_{31} & H_{32} & H_{33} \end{pmatrix}^T$ .
Теперь систему уравнений можно перевести в матричный вид: $A = \begin{pmatrix} ... \\ v_x & v_y & 1 & 0 & 0 & 0 & - v_x \cdot {p_i}_x & - v_y \cdot {p_i}_x & - {p_i}_x \\ 0 & 0 & 0 & v_x & v_y & 1 & - v_x \cdot {p_i}_y & - v_y \cdot {p_i}_y & - {p_i}_y \\ ... \end{pmatrix}$
$A \cdot \vec{h} = \vec{0}$
Получили однородную систему уравнений в которой нам неизвестен вектор $\vec{h}$ (т.е. матрица $inline$ ). Однородную систему уравнений мы не сможем решить при помощи метода наименьших квадратов. Однако одно решение найти несложно — это нулевой вектор — $\vec{h} = \vec{0}$ . Но такое решение нас не интересует. Если же система имеет какое-то ненулевое решение, то мы получаем сразу бесконечное множество решений. Для примера пусть мы уже имеем ненулевое решение — вектор $\vec{h}$ : $A \cdot \vec{h} = \vec{0}$ . Теперь умножим вектор $\vec{h}$ на любой ненулевой скаляр $inline$ , система уравнений все равно останется справедливой, а $\vec{h} \cdot s$ — также будет еще одним решением системы: $A \cdot \vec{h} \cdot s = \vec{0}$ . Так как мы работаем с однородными координатами, то умножение на скаляр ничего не меняет. Тем не менее, чтобы не работать сразу со множеством решений, будем искать только одно — пусть длина вектора будет равна единицы $|\vec{h}| = 1$ .

Сингулярное разложение и решение однородных систем уравнений

Решить однородную систему уравнений можно при помощи сингулярного разложения матрицы (singular value decomposition). Сингулярное разложение — это разложение вида: $svd(M) = U \cdot W \cdot V^T$ , где $inline$ и $inline$ — ортонормальные матрицы, а $inline$ — диагональная, при этом диагональные элементы больше либо равны нулю и располагаются в порядке убывания (сверху вниз). Если воспринимать матрицу как операцию трансформации векторов, то это разложение будет декомпозицией этой трансформации на три последовательных: поворот, масштабирование по осям, второй поворот. Матрицы $inline$ и $inline$ — это ортонормальные матрицы, а значит можно назвать их матрицами поворота. Только следует учитывать, что $|U| = \pm 1$ и $|V| = \pm 1$ , а значит, например, если $inline$ — имеет размер 3x3, то тройка базисных векторов и этих матриц поворота могут быть левосторонними, а не правосторонними как обычно.

Не будем останавливаться на том, как вычислять это разложение. В более-менее полноценных математических фреймворках оно будет реализовано. Например — Eigen.

Воспользуемся этим разложением для полученной выше матрицы $inline$ : $svd(A) = U \cdot W \cdot V^T$ . Лучшее решение для нашей системы уравнений $A \cdot \vec{h} = \vec{0}$ — это последняя строка матрицы $inline$ : $\vec{h} = V_{n}$ . А так как матрица $inline$ — ортонормальная, то длина вектора, составленного из любого его столбца, будет равна как раз единице.

Доказательство

В процессе вычислений у нас всегда есть погрешность, а это значит после $A \cdot \vec{h}$ мы можем получить не нулевой вектор, хотя его компоненты должны быть близки к нулю. Нужно минимизировать получаемую погрешность, а для ее оценки воспользуемся обычной для таких вещей суммой квадратов: $\vec{e} = \sum{{e_i}^2} = \vec{e}^T \vec{e} \rightarrow min$ .
$\vec{e} = H \cdot \vec{h} \Rightarrow \vec{e}^T \vec{e} = (H \cdot \vec{h})^T (H \cdot \vec{h}) = (U \cdot W \cdot V^T \cdot \vec{h})^T (U \cdot W \cdot V^T \cdot \vec{h}) \rightarrow min$
$E = \vec{e}^T \vec{e} = \vec{h}^T \cdot V \cdot W \cdot U^T \cdot U \cdot W \cdot V^T \cdot \vec{h}$ , так как $inline$ — ортонормальная матрица, то $U^T \cdot U = I$ . Так как $inline$ — диагональная матрица с ненулевыми элементами, расположенными по убыванию, то и $(W^T \cdot W)$ — также будет диагональной матрицей с ненулевыми элементами, расположенными по убыванию — это будет эквивалентно возведению в квадрат диагональных элементов матрицы. Обозначим $W^2 = W^T \cdot W$ .
$E = \vec{e}^T \vec{e} = \vec{h}^T \cdot V \cdot W^2 \cdot V^T \cdot \vec{h} \rightarrow min$
Обозначим $\vec{c} = V^T \cdot \vec{h}$ , заметим, что $inline$ — не сохраняет длину вектора $\vec{h}$ , значит $|\vec{c}| = 1$ :
$E = \vec{c}^T \cdot W^2 \cdot \vec{c} \rightarrow min$ .
Представим диагональ матрицы $inline$ как вектор $\vec{w}$ . Тогда $E = \vec{c}^T \cdot W^2 \cdot \vec{c} = \sum{{c_i}^2 \cdot {w_i}^2} \rightarrow min$
Теперь подумаем чему должен быть равен $\vec{c}$ , чтобы $inline$ стало минимальным. Так как значения в $\vec{w}$ . Судя по $\sum{{c_i}^2 \cdot {w_i}^2}$ , наибольший вклад должен вносить последняя компонента вектора $\vec{w}$ . Так как $|\vec{c}| = 1$ , то выходит $\vec{c} = \begin{pmatrix} 0 & ... & 0 & 1 \end{pmatrix}^T$ .
$\begin{pmatrix} 0 & ... & 0 & 1 \end{pmatrix}^T = V^T \cdot \vec{h} \Rightarrow \vec{h} = V \cdot \begin{pmatrix} 0 & ... & 0 & 1 \end{pmatrix}^T$ .
Из описанного выше делаем вывод, что $\vec{h} = V_n$ — это последний столбец матрицы $inline$ .

Возвращаемся к нашей системе уравнений $A \cdot \vec{h} = \vec{0}$ . Решаем ее описанным выше способом, получаем вектор $\vec{h}$ . Затем из этого уже получаем искомую матрицу $inline$ . Пробуем:

Homography

Как мы видим стало заметно лучше и искажения уже похожи на правду.
Соответствующий код для аффинных и перспективных искажений можно найти в тестах проекта — sonar/tests/test_marker_transform

Pinhole camera model

Хорошо, мы получили какую-то матрицу для преобразования изображений, но в идеале хотелось бы получить координаты камеры в пространстве. Чтобы их найти, построим математическую модель, которая будет описывать как точки мирового пространства проецируются на изображение камеры.

В качестве модели формирования изображения возьмем центральную проекцию. Суть центральной проекции состоит в том, что все точки, которые формируют выходное изображение, формируют лучи, сходящиеся в одной точке — центре проекции. Примерно так лучи себя и ведут в модели глаза или в цифровой камере.

Проецировать точки будем на плоскость, которая и будет формировать наше изображение. В качестве такой плоскости возьмем плоскость, заданную таким условием $inline$ . В таком случае наша камера будет сонаправлена с осью $inline$ :

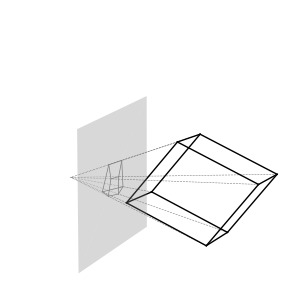
Зададим параметрически формулу луча, формирующего точку на проекции: $\vec{r} = \vec{v} \cdot t$ , где $\vec{r}$ — координаты точки луча, $\vec{v}$ — координаты проецируемой точки, а $inline$ — является свободным параметром. Если луч не лежит на нашей плоскости и не параллелен ей, то он будет пересекать ее только в одной точке. При этом мы знаем, что $inline$ .
$r_z = v_z \cdot t \Rightarrow t = \frac{1}{v_z}$
$\vec{r} = \vec{v} \cdot t = \vec{v} \cdot \frac{1}{v_z} = \begin{pmatrix} \frac{v_x}{v_z} & \frac{v_y}{v_z} & 1\end{pmatrix}$
Получаем координаты спроецированной на плоскость точки: $\vec{p} = \begin{pmatrix} \frac{v_x}{v_z} & \frac{v_y}{v_z}\end{pmatrix}$ . Ничего не напоминает? Это формула перевода из однородных координат в двумерные евклидовы. Получается, что трехмерные координаты можно воспринимать как однородные координаты, соответствующие двумерным евклидовым координатам на плоскости. А перевод из однородных координат в двумерные евклидовы координаты выполняет центральную проекцию. Можно сказать, что трехмерные евклидово пространство эквивалентно двумерному проекционному.

После проецирования точки на плоскость можно переводить ее в координаты изображения. Обычно координаты изображения определены следующим образом, где $inline$ и $inline$ — высота и ширина изображения:

Пусть у нас для камеры задан угол обзора по горизонтали — $inline$ .
Масштабируем координату $inline$ точки $inline$ так, чтобы расстояние от крайней левой видимой точки камеры до крайней правой было равно ширине изображения. При проецировании имеем такую картину:

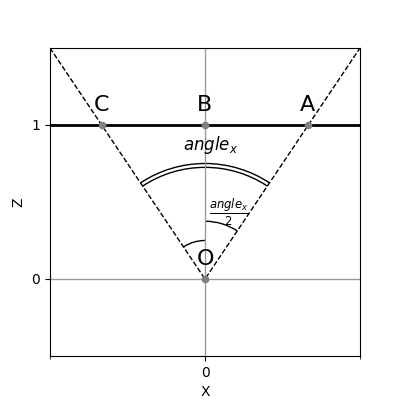
Image coordinates

Здесь $inline$ — левая и правые крайние точки, $inline$ — точка между ними, у которой координата $inline$ , а $inline$ . Угол $\angle{AOC} = angle_x$ . При этом имеем треугольник $inline$ , у которого угол $\angle{ABO} = 90^{\circ}$ , а угол $\angle{AOB} = \frac{angle_x}{2}$ , так как $inline$ делит угол $\angle{AOC}$ пополам. Длина $inline$ равна 1. Отсюда через тангенс угла $\angle{AOB}$ найдем длину $inline$ — $\tan{\angle{AOB}} = \tan{\frac{angle_x}{2}} = \frac{AB}{OB} = AB$ . А уже отсюда $AC = 2 \cdot AB = 2 \cdot \tan{\frac{angle_x}{2}}$ .
После проецирования сводим диапазон координаты $inline$ — $[- \tan{\frac{angle_x}{2}}, \tan{\frac{angle_x}{2}}]$ к диапазону $[- \frac{width}{2}, \frac{width}{2}]$ умножением на коэффициент:
$f_x = \frac{width}{2 \cdot \tan{\frac{angle_x}{2}}}, \space x' = x \cdot f_x$
Чтобы сохранить пропорции изображения, то координату $inline$ мы должны масштабировать на ту же величину. Но на выходном изображении ось $inline$ направлена в обратную сторону (вниз). Чтобы отразить ось, умножим коэффициент масштаба по оси $inline$ на $inline$ . Получаем такое преобразование:
$f_y = - f_x, \space , \space \space y' = y \cdot f_y$
$\vec{p'} = \begin{pmatrix} f_x \cdot p_x & f_y \cdot p_y \end{pmatrix}^T$
А координаты видимого изображения получили такой диапазон:

Image range

Получилось так, что центр изображения — нулевая точка. Чтобы получить нужные на координаты на изображении, сместим крайнюю левую точку в центр:
$\vec{p'} = \begin{pmatrix} f_x \cdot p_x & f_y \cdot p_y \end{pmatrix}^T + \begin{pmatrix} \frac{width}{2} & \frac{height}{2} \end{pmatrix}^T$
Теперь центральная точка изображения будет иметь координаты $\begin{pmatrix} \frac{width}{2} & \frac{height}{2} \end{pmatrix}^T$ , как ей и положено. Эта центральная называется оптическим центром, обозначим ее как $\vec{c} = \begin{pmatrix} \frac{width}{2} & \frac{height}{2} \end{pmatrix}^T$ . И финальная формула преобразования в координаты изображения:
$\vec{p'} = \begin{pmatrix} f_x \cdot p_x & f_y \cdot p_y \end{pmatrix}^T + \vec{c}$ , где $f_x = \frac{width}{2 \cdot \tan{\frac{angle_x}{2}}}, \space f_y = - f_x$ , а $\vec{c} = \begin{pmatrix} \frac{width}{2} & \frac{height}{2} \end{pmatrix}^T$ .
Также, как мы делали до этого, можно упростить преобразование, работая сразу с однородными координатами точки и трансформируя все выражения в матричную форму:
Пусть $K = \begin{pmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{pmatrix}$ , тогда $\vec{p'} = project(K \cdot \begin{pmatrix} p_x \\ p_y \\ 1\end{pmatrix})$ .
Возвращаемся немного назад. Вспоминаем, что трехмерном пространстве — это проективное пространство для плоскости, на которую мы проецируем. Т.е. трехмерные координаты — это однородные координаты. Тогда формула перевода из трехмерного пространства в координаты изображения при центральной проекции принимает вид:
$\vec{p'} = project(K \cdot \begin{pmatrix} v_x \\ v_y \\ v_z \end{pmatrix}) = project(K \cdot \vec{v})$
Матрицу $inline$ — называют внутренними параметрами камеры (intrinsic camera parameters).

Эта матрица может в себе иметь еще параметр $s_{skew}$ :
$K = \begin{pmatrix} f_x & s_{skew} & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{pmatrix}$ .
Эффект от его применения чем схож эффектом от rolling shutter. На практике обычно этот параметр не учитывается и остается равно нулю.

Следует учитывать, что формулы вычисления параметров $inline$ справедливы, если мы хотим перевести именно в пиксельные координаты изображения. Но других случаях нам может быть нужно перевести в другую координатную систему, например, в текстурные координаты, где значения координат $inline$ и $inline$ меняются в диапазоне $inline$ . Тогда эти параметрами будут уже другими.

Погрешности на производстве при сборки камер немного сказываются и на получаемых с них изображениях, оптический центр смещается немного от центра изображения, а каждая камера имеет слегка отличающиеся внутренние параметры. Поэтому каждая камера калибруется индивидуально. Реализацию калибровки можно найти в OpenCV.

В API Android OS и iOS можно найти методы получения внутренних параметров камеры, заданные производителем.

Сейчас же предлагаю просто считать оптическим центром — центр изображения, а параметры $inline$ подбирать "на глаз". Для начала хватит и такого варианта.

Перемещение камеры в пространстве

Все относительно — и хотя наблюдатель перемещается в пространстве, а мир стоит на месте, мы также можем сказать, что движется мир, а наблюдатель остается на месте. Меняется только система координат, в которой происходит движение. Значит выберем ту, которая для нас удобнее. А удобнее нам оставить локальную систему координат на месте, и все остальное пусть движется вокруг нее. Движение у нас определяется поворотом и смещением — матрицей поворота $inline$ и вектором смещения $\vec{t}$ . Также считаем, что у нас есть внутренние параметры камеры, заданные матрицей $inline$ . Таким образом мы можем разбить процесс вычисления координат на изображении из мировых координат на два этапа:

Перевод мировых координат $\vec{v}$ в локальные координаты камеры $\vec{v'}$ при помощи $inline$ и $\vec{t}$ : $\vec{v'} = R \cdot \vec{v} + \vec{t}$
Перевод из локальных координат камеры в пиксельные координаты изображения при помощи матрицы $inline$ : $\vec{p} = project(K \cdot \vec{v'})$

Как мы уже знаем, матрицу $inline$ и вектор $\vec{t}$ можно объединить в одну матрицу, только для того, чтобы ее применить придется перевести $\vec{v}$ в однородные координаты:
$\begin{pmatrix} {v'}_x \\ {v'}_y \\ {v'}_z \\ 1 \end{pmatrix} = \begin{pmatrix} R_{11} & R_{12} & R_{13} & t_x \\ R_{21} & R_{22} & R_{23} & t_y \\ R_{31} & R_{32} & R_{33} & t_z \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} v_x \\ v_y \\ v_z \\ 1 \end{pmatrix}$
Мы знаем, что ${v'}_w = 1$ и нам необязательно ее вычислять, поэтому можем чуть сократить формулу:
$\begin{pmatrix} {v'}_x \\ {v'}_y \\ {v'}_z \end{pmatrix} = \begin{pmatrix} R_{11} & R_{12} & R_{13} & t_x \\ R_{21} & R_{22} & R_{23} & t_y \\ R_{31} & R_{32} & R_{33} & t_z\end{pmatrix} \begin{pmatrix} v_x \\ v_y \\ v_z \\ 1 \end{pmatrix}$
Более короткая версия этой же формулы:
$\vec{v'} = [R | \vec{t}] \begin{pmatrix} \vec{v} \\ 1 \end{pmatrix}$
Теперь мы можем объединить два этапа в одну формулу:
$\vec{p} = project(K \cdot [R | \vec{t}] \begin{pmatrix} \vec{v} \\ 1 \end{pmatrix})$
К этому моменту можно нас поздравить — мы построили математическую модель проецирования изображения камеры. Опираясь на нее далее мы сможем понять, что происходит в видеопотоке. А точнее нашей основной задачей станет поиск параметров $inline$ и $\vec{t}$ . Эти параметры называют внешними параметрами камеры (extrinsic camera parameters). Так как мы предположили, что камера остается на месте, а двигается окружающий мир, то $inline$ — это не матрица поворота самой камеры, а вектор $\vec{t}$ — не координаты позиции камеры. Матрица $inline$ — это поворот из мировых координат в локальные координаты камеры, а когда говорят о повороте объекта, то имеют ввиду поворот из локальных координат в мировые. Поэтому поворот камеры — это $R_{camera} = R^{-1}$ . Вектор $\vec{t}$ — вектор смещения камеры. Позицию камеры в мировых координатах можем найти следуя такой логике: при переводе в локальные координаты позиция камеры должна стать нулевым вектором — $\vec{0} = R \cdot \vec{pos_{camera}} + \vec{t} \space \Rightarrow \space (\vec{0} - \vec{t}) = R \cdot \vec{pos_{camera}} \space \Rightarrow \space \vec{pos_{camera}} = - R^{-1} \cdot \vec{t}$ .

Получаем координаты камеры от маркера

Возвращаемся к предыдущему примеру. В нем мы нашли перспективную матрицу $inline$ , описывающую преобразования наших точек:
$\vec{p_i} = project(H \cdot \begin{pmatrix} {v_i}_x \\ {v_i}_y \\ 1 \end{pmatrix})$
Попробуем разобраться как эта формула соотноситься с нашей моделью:
$\vec{p} = project(K \cdot [R | \vec{t}] \begin{pmatrix} \vec{v} \\ 1 \end{pmatrix}) = project(K \cdot \begin{pmatrix} R_{11} & R_{12} & R_{13} & t_x \\ R_{21} & R_{22} & R_{23} & t_y \\ R_{31} & R_{32} & R_{33} & t_z \end{pmatrix} \begin{pmatrix} v_x \\ v_y \\ v_z \\ 1 \end{pmatrix})$
Точки маркера в нашем случае задаются двумерными координатами, так как они все лежат на плоскости, т.е. $inline$ . А так как $inline$ , то столбец $\begin{pmatrix} R_{13} \\ R_{23} \\ R_{33} \end{pmatrix}$ не вносит вклада в результат, а значит его можно вычеркнуть, сократив формулу:
$\vec{p} = project(K \cdot \begin{pmatrix} R_{11} & R_{12} & t_x \\ R_{21} & R_{22} & t_y \\ R_{31} & R_{32} & t_z \end{pmatrix} \begin{pmatrix} v_x \\ v_y \\ 1 \end{pmatrix})$
Пусть $H' = K \cdot \begin{pmatrix} R_{11} & R_{12} & t_x \\ R_{21} & R_{22} & t_y \\ R_{31} & R_{32} & t_z \end{pmatrix}$ , тогда получаем:
$\vec{p_i} = project(H' \cdot \begin{pmatrix} {v_i}_x \\ {v_i}_y \\ 1 \end{pmatrix})$
Получили идентичную формулу. Но сделать вывод, что $inline$ — нельзя. При вычислении матрицы $inline$ мы получили целое множество решений и выбрали из этого множества удобное для нас. При работе с однородными координатами умножение на скаляр не играет роли, но в нашей модели мы уже оперируем трехмерными евклидовыми координатами. Поэтому $s \cdot H' = H$ . Отсюда:
$H = s \cdot K [R | \vec{t}] = K \cdot \begin{pmatrix} s \cdot R_{11} & s \cdot R_{12} & s \cdot t_x \\ s \cdot R_{21} & s \cdot R_{22} & s \cdot t_y \\ s \cdot R_{31} & s \cdot R_{32} & s \cdot t_z \end{pmatrix}$ .
Пусть $T = K^{-1} \cdot H = \begin{pmatrix} s \cdot R_{11} & s \cdot R_{12} & s \cdot t_x \\ s \cdot R_{21} & s \cdot R_{22} & s \cdot t_y \\ s \cdot R_{31} & s \cdot R_{32} & s \cdot t_z \end{pmatrix} = K^{-1} \cdot H$
Первые два столбца полученной матрицы составляют два базисных вектора матрицы поворота. Длины этих векторов должны быть равны единице. Отсюда мы можем найти параметр $s = |\begin{pmatrix} T_{11} & T_{21} & T_{31} \end{pmatrix}^T| = |\begin{pmatrix} T_{12} & T_{22} & T_{32} \end{pmatrix}^T|$ . Из-за погрешностей вычислений первый и второй вариант вычислений будут давать немного разные варианты, поэтому возьмем среднее между ними: $s = \frac{|\begin{pmatrix} T_{11} & T_{21} & T_{31} \end{pmatrix}^T| + |\begin{pmatrix} T_{12} & T_{22} & T_{32} \end{pmatrix}^T|}{2}$ .
Теперь вычислим два базисных вектора матрицы поворота:
$\vec{r_1} = \frac{\begin{pmatrix} T_{11} & T_{21} & T_{31} \end{pmatrix}^T}{|\begin{pmatrix} T_{11} & T_{21} & T_{31} \end{pmatrix}^T|}$
$\vec{r_2} = \frac{\begin{pmatrix} T_{12} & T_{22} & T_{32} \end{pmatrix}^T}{|\begin{pmatrix} T_{12} & T_{22} & T_{32} \end{pmatrix}^T|}$
$R = \begin{pmatrix} \vec{r_1} & \vec{r_2} & \vec{r_1} \times \vec{r_2} \end{pmatrix}$
$\vec{t} = \frac{\begin{pmatrix} T_{13} & T_{23} & T_{33} \end{pmatrix}^T}{s}$
$R_{camera} = R^{-1}, \space \vec{pos_{camera}} = - R^{-1} \cdot \vec{t}$
Итак, мы получили координаты камеры в пространстве. Теперь можем передать эти координаты трехмерному движку, чтобы он вывел трехмерные модели поверх реального изображения. Что и было реализовано в плагине для Unity. Видео, записанное с android-сматфона:

Точки маркера, на которых мы основываем нашу мировую систему координат в наших вычислениях и которая одновременно с этим является нашим полом, находятся в плоскости $inline$ . У Unity же пол является плоскостью $inline$ . Чтобы повернуть пол в нужные нам координаты, я воспользовался встроенными в Unity средствами — создал пустой объект, назначил его "родителем" камеры, и повернул так, как мне нужно. Таким образом, мне самому не пришлось делать дополнительных вычислений. Также важно сопоставить характеристики виртуальной камеры и реальной. Пример этого можно увидеть в коде плагина.

Нужно еще отметить, что описать преобразование точек при помощи перспективной матрицы размером 3x3 можно только в случае, когда идет отображение точек с одной плоскости на другую. Такая матрица называется матрицей гомографии (homography matrix). В нашем случае шло отображение с плоскости маркера на плоскость проекции. Но при работе трехмерными координатами алгоритм direct linear transformation задействовать уже не получится и нужно будет искать другие способы.

Заключение

Код, реализующий все примеры выше можно найти в проекте на гитхаб в ветке article2.

Точность пока оставляет желать лучшего. Более того, маркеры являются не самом удобным способ взаимодействия с дополненной реальностью, поэтому далее будем пытаться отойти от их использования и улучшать точность работы.

Теги:

Хабы: