Не знаю как вам, а мне статистика далась очень не просто. Причем "далась" - это еще громко сказано. Да, оказалось что можно довольно долго ехать на методичках, кое как вникая в смысл четырехэтажных формул, а иногда даже не понимая результатов, но все равно ехать. Ехать и не получать никакого удовольствия - вроде бы все понятно, но ощущение, что ты "не совсем в теме" все никак не покидает. Какое-то время пытался читать книги по R и не то что бы совсем безрезультатно, но и не "огонь". Нашел наикрутейшую книгу "Статистика для всех" Сары Бослаф, прочитал... все равно остались какие-то нюансы смысл которых так и не понятен до конца.
В общем, как вы догадались - эта статья из серии "Пробую объяснить на пальцах, что бы самому разобраться." Так что если вы неравнодушны к статистике, то прошу под кат.
Я предполагаю, что вы уже знакомы с основами теории вероятности, поэтому здесь не будет математических выкладок и строгих доказательств. Если нет, то рекомендую почитать следующие книги:
"Теория вероятности и математическая статистика" Л. Н. Фадеева, А. В. Лебедев;
"Теория вероятности и математическая статистика" Н. Ш. Кремер. Эти две книги на, мой взгляд, лучшие для первого знакомства с "тервером и статами". Вовсе не рекомендую вгрызаться в эти книги, продолжайте читать даже если что-то непонятно, просто для того что бы оценить "широту картинки" и привыкнуть к терминологии. Конечно, советовать продолжать читать, даже если что-то непонятно - это не комильфо. Но есть еще одна хорошая книга:
"Теория вероятности и математическая статистика" В. П. Лисьев. В ней гораздо больше примеров и разъяснений. Так что если первые две книги не "побеждаются", то можете смело браться за Лисьева. Однако в первых двух книгах очень хорошее введение в теорию вероятности.
Ну и наконец книга "Статистика для всех" Сара Бослаф. Я бы порекомендовал для прочтения только эту книгу, но мне кажется, что если бы я ее читал, абсолютно не зная теорию вероятности и мат. статистику, то я бы очень много вообще не понял, ну или очень долго вникал в текст, формулы и картинки. Там конечно есть разделы с основами для конкретных новичков, но на мне такое не работает. Хотя, более чем вероятно, что этой книги для вас этого окажется более чем достаточно. В книге намеренно нет примеров с кодом, но это скорее плюс чем минус, потому что в книге есть примеры численных расчетов. Так что можно кодить и сравнивать свои результаты с результатами из книги.
Конечно в интернете море всякой литературы, но как пишет Сара в своей книге "Вода, вода, кругом вода, а мы не пьем", намекая на то, что книг море, но самоучки умирают от "жажды".
Вместо того что бы развозить математику и доказательства (кто-то скажет, что это кощунство) я предлагаю немного покодить и пойти по принципу "если что-то непонятно то моделируй и экспериментируй до тех пор пока не станет понятно". Само программирование потребует от нас хотя бы небольших познаний библиотек NumPy, matplotlib, seaborn и SciPy - открытых вкладок с документацией будет более чем достаточно. Итак, начнем.
Пример не для тех кто проголодался
Давайте представим... так постойте, прежде чем что-то представлять давайте сделаем все необходимые импорты и настройки:
import numpy as np from scipy import stats import matplotlib.pyplot as plt #import seaborn as sns from pylab import rcParams #sns.set() rcParams['figure.figsize'] = 10, 6 %config InlineBackend.figure_format = 'svg' np.random.seed(42)
Вот теперь давайте представим, что в течение года мы заказываем пиццу на дом, при этом мы каждый раз смотрим на стенные стрелочные часы, отмечая время, которое проходит между заказом и доставкой, целым количеством минут. Тогда накопленные за год данные о доставке пиццы могли бы выглядеть так:
norm_rv = stats.norm(loc=30, scale=5) samples = np.trunc(norm_rv.rvs(365)) samples[:30]
array([32., 29., 33., 37., 28., 28., 37., 33., 27., 32., 27., 27., 31., 20., 21., 27., 24., 31., 25., 22., 37., 28., 30., 22., 27., 30., 24., 31., 26., 28.])
Конечно же теперь нам интересно выяснить среднее время доставки пиццы и его среднеквадратическое отклонение:
samples.mean(), samples.std()
(29.52054794520548, 4.77410133275075)
Можно сказать, что время доставки пиццы занимает где-то минут.
А еще, было бы интересно посмотреть на то, как распределены данные:
sns.histplot(x=samples, discrete=True);
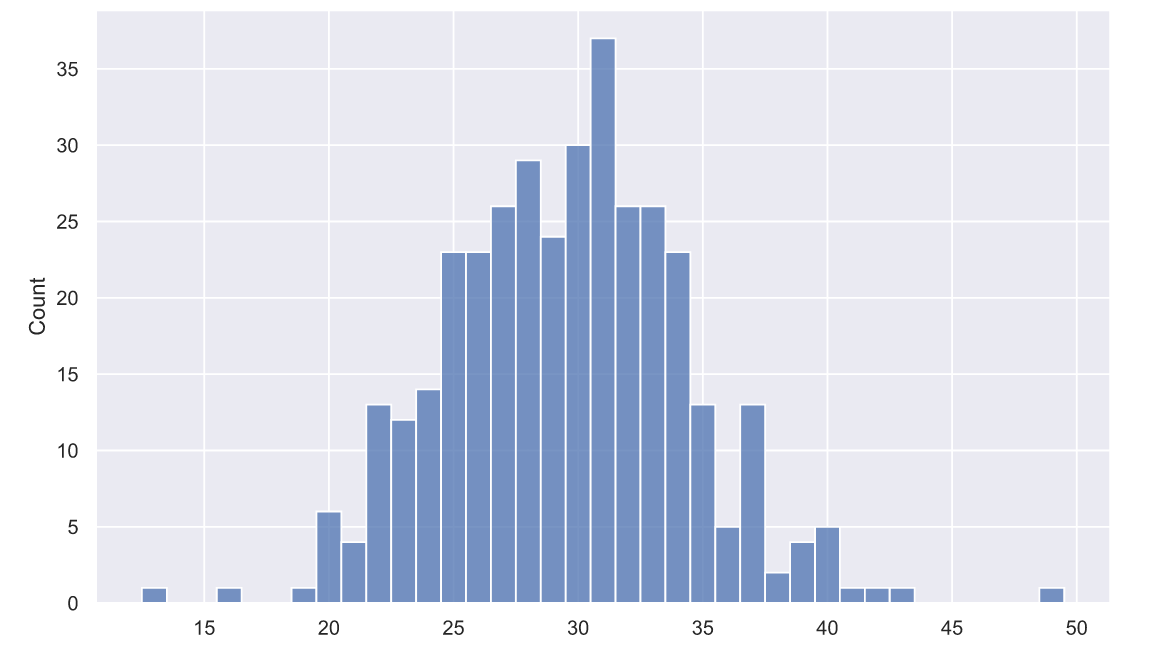
Глядя на такой график, мы вполне можем допустить, что время доставки пиццы имеет нормальный закон распределения с параметрами и
. Кстати, а почему мы решили, что распределение нормальное? Потому что гистограмма хорошо смотрится на фоне функции распределения плотности вероятности нормального распределения? Если речь идет о визуальном предпочтении, то с таким же успехом мы можем подогнать и нарисовать функции распределений плотности гамма, бета и даже треугольного распределения:
norm_rv = stats.norm(loc=30, scale=5) beta_rv = stats.beta(a=5, b=5, loc=14, scale=32) gamma_rv = stats.gamma(a = 20, loc = 7, scale=1.2) tri_rv = stats.triang(c=0.5, loc=17, scale=26) x = np.linspace(10, 50, 300) sns.lineplot(x = x, y = norm_rv.pdf(x), color='r', label='norm') sns.lineplot(x = x, y = beta_rv.pdf(x), color='g', label='beta') sns.lineplot(x = x, y = gamma_rv.pdf(x), color='k', label='gamma') sns.lineplot(x = x, y = tri_rv.pdf(x), color='b', label='triang') sns.histplot(x=samples, discrete=True, stat='probability', alpha=0.2);
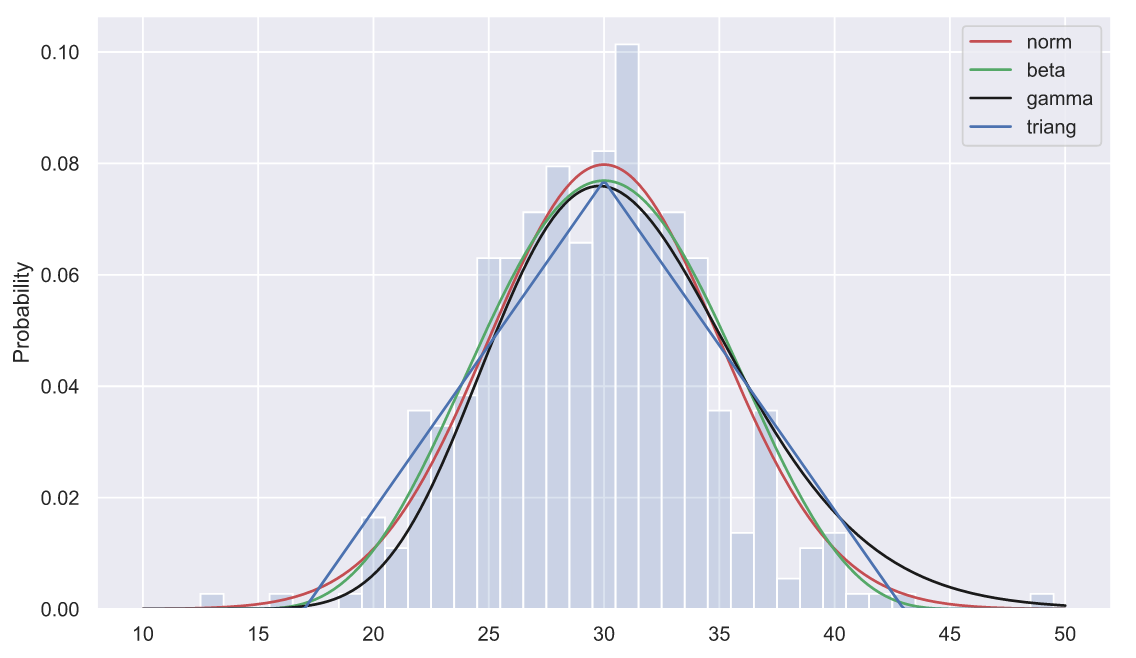
Распределение точно нормальное?
Доставкой пицы занимается человек, а сам процесс доставки сопровождается множеством случайных событий которые могут произойти на его пути:
на перекрестке пришлось ждать две минуты пока светофор загорится зеленым;
ударился ногой и из-за хромоты шел дольше обычного;
доставщик оказался скейтбордистом и передвигался быстрее обычного;
дорогу перебежала черная кошка и пришлось идти другим более долгим путем;
развязались шнурки и пришлось тратить время на их завязывание;
развязались шнурки и доставщик упал, поэтому пришлось тратить время на отряхивание грязи и завязывание шнурков.
Конечно, мы можем придумывать очень много таких событий, вплоть до самых невероятных (возможно одна из дорог в Ад вымощена не доставленными пиццами, поэтому мы не будем выдумывать что-то обидное. Ок?). Тем не менее, для нас важно что бы эти события описывались такими переменными, значения которых равновероятны, т.е. распределены по равномерному закону. В качестве примера, можно придумать переменную , которая будет описывать время ожидания зеленого света светофора на перекрестке. Если это время заключено в промежутке от нуля до четырех минут, то сегодня это время может составлять:
unif_rv = stats.uniform(loc=0, scale=4) unif_rv.rvs()
0.8943833540778106
А завтра, после-завтра и после-после-завтра это время может быть равно:
unif_rv.rvs(size=3)
array([3.85289016, 0.0486179 , 3.87951531])
Теперь представим, что таких переменных 15 и значение каждой из них вносит свой вклад в общее время доставки, потому что эти события могут складываться. К примеру, если бы я был доставщиком то я:
мог замечтаться и только где-то в пути вспомнить, что забыл пиццу - т.е. вернуться за пиццей один раз;
мог забыть пиццу, вернуться за ней, а потом вспомнить, что взял не ту пиццу - т.е. вернуться за пицей два раза;
мог сначала забыть пиццу, потом вспомнить, что взял не ту пиццу, вернуться за другой пиццей, а потом где-то в пути случайно ее уронить - т.е. вернуться за пиццей три раза.
Если мы придумали всего 15 случайных переменных: , то можно сказать, что общее время доставки является их суммой и тоже является случайной величиной, которую можно обозначить буквой
:
Но если значения каждой из переменных распределены равномерно, то как будет распределена их сумма - переменная
? Давайте сгенерируем 10 тысяч таких сумм и посмотрим на гистограмму:
Y_samples = [unif_rv.rvs(size=15).sum() for i in range(10000)] sns.histplot(x=Y_samples);
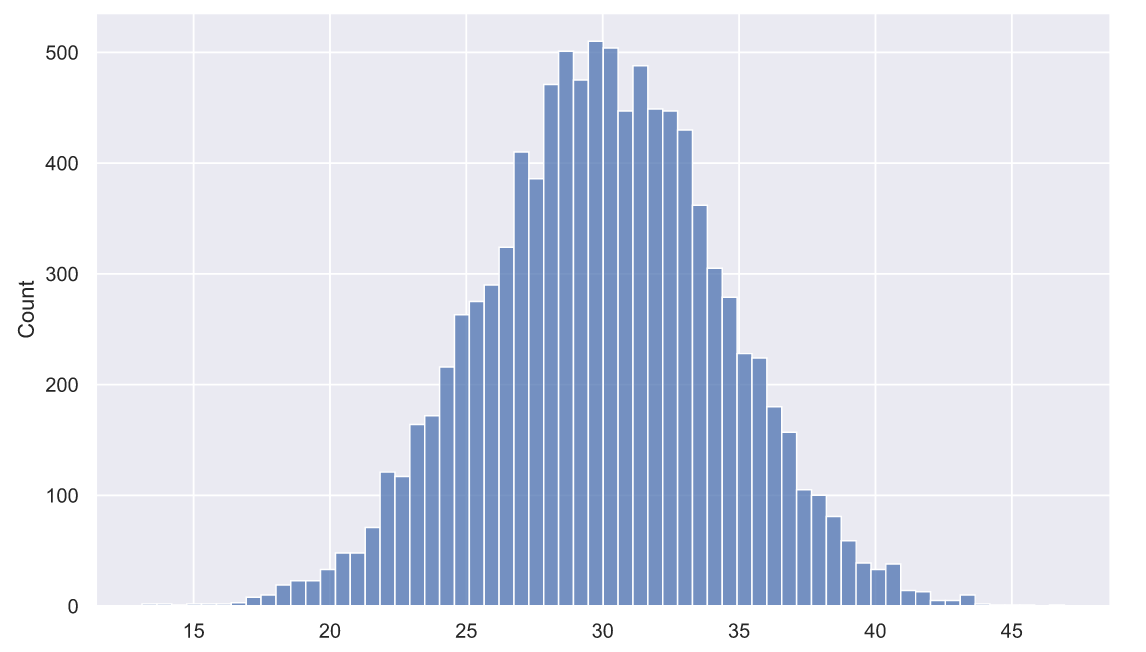
Не напоминает ли вам эта картинка тот самый колокол, того самого нормального распределения? Если напоминает, то вы только, что поняли смысл центральной предельной теоремы: распределение суммы случайных переменных стремится к нормальному распределению при увеличении количества слагаемых в этой сумме.
Конечно, пример с доставкой пиццы не совсем корректен для демонстрации предельной теоремы, потому что все события которые мы придумали носят условный характер:
на перекрестке пришлось ждать две минуты пока светофор загорится зеленым. Но ждать придется только если мы подошли к светофору, который уже горит красным;
ударился ногой и из-за хромоты шел дольше обычного. Но с какой-то вероятностью мы можем и не удариться;
доставщик оказался скейтбордистом и передвигался быстрее обычного. При условии что он не забыл скейтборд дома;
дорогу перебежала черная кошка и пришлось идти другим более долгим путем. Существует ненулевая вероятность того, что доставщик не является фанатом бабы Нины;
развязались шнурки и пришлось тратить время на их завязывание. Как часто развязываются шнурки?;
развязались шнурки и доставщик упал, поэтому пришлось тратить время на отряхивание грязи и завязывание шнурков. Если дворник не халтурит, то и ни от какой грязи отряхиваться не надо.
А то, что каждая из переменных носит условный характер означает, что они могут входить в сумму в самых разных комбинациях. Например, сегодня время доставки задавалось, как:
А завтра это время может задаваться как:
Будет ли теперь распределена нормально? Учитывая что сумма нормально распределенных величин тоже имеет нормальное распределение, то можно дать утвердительный ответ. Именно поэтому, когда мы взглянули на распределение 365-и значений времени доставки, мы практически сразу решили, что перед нами нормальное распределение, даже несмотря на то что оно вовсе не похоже на идеальный колокол.
Z-значения
Допустим, по прошествии года у нас появился новый сосед и он так же как и мы решил ежедневно заказывать пиццу. И вот по прошествии трех дней мы наблюдаем, как этот сосед обвиняет доставщика в слишком долгом ожидании заказа. Мы решаем поддержать доставщика и говорим, что в среднем время доставки занимает минут, на что наш сосед отвечает, что все три раза он ждал больше 40 минут, а это всяко больше 35 минут.
Почему наш сосед так уверен в долгой доставке? И вообще, оправдана ли его уверенность? Очевидно он, как и некоторые люди, думает, что минут означает, что доставка может длиться 27, 31, даже 35 минут, но никак не 23 или 38 минут. Однако, мы заказывали пиццу 365 раз и знаем, что доставка может длиться и 20 и даже 45 минут. А фраза
минут, означает лишь то, что какая-то значительная часть доставок бодет занимать от 25 до 35 минут. Зная параметры распределения, мы даже можем смоделировать несколько тысяч доставок и прикинуть величину этой части:
N = 5000 t_data = norm_rv.rvs(N) t_data[(25 < t_data) & (t_data < 35)].size/N
0.7008
Где-то две трети значений укладываются в интервал от 25 до 35 минут. А сколько значений будет превосходить 40 минут?
t_data[t_data > 40].size/N
0.0248
Оказывается только чуть более двух процентов значений превосходят 40 минут. Но ведь сосед заказывал пиццу три раза подряд и все три раза доставка длилась больше 40 минут. Может сосед оказался просто очень везучим, ведь вероятность трех таких долгих доставок чрезвычайно мала:
0.02**3
8.000000000000001e-06
Конечно, компьютерное моделирование - это очень хорошо. Но в данном случае лучше воспользоваться так называемыми Z-значениями.
Вычислить Z-значение можно по следующей формуле:
Где - это время доставки, т.е. какое-то конкретное значение случайной переменной
, которая имеет нормальное распределение, а
и
это мат. ожидание и среднеквадратическое отклонение, т.е. параметры распределения, в нашем случае они равны 30 и 5 минут соответственно. Давайте рассчитаем Z-значение для сорока минут:
Что мы сейчас сделали? В числителе мы вычислили на какую величину наше время доставки отличается от среднего времени доставки, а далее мы просто поделили это значение на стандартное отклонение времени доставки. Но как интерпретировать данный результат и зачем вообще использовать Z-значение? Что бы понять это придется немного "порисовать":
fig, ax = plt.subplots() x = np.linspace(norm_rv.ppf(0.001), norm_rv.ppf(0.999), 200) ax.vlines(40.5, 0, 0.1, color='k', lw=2) sns.lineplot(x=x, y=norm_rv.pdf(x), color='r', lw=3) sns.histplot(x=samples, stat='probability', discrete=True);
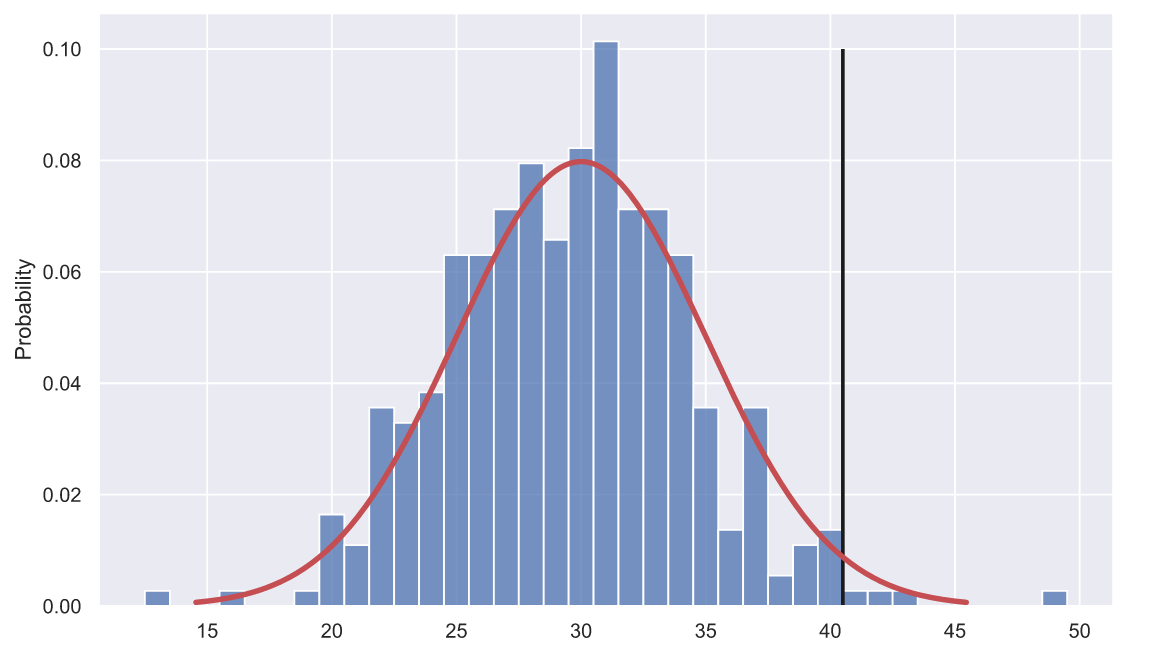
На данном графике мы изобразили гистограмму наших данных samples, но теперь высота прямоугольников показывает не количество вхождений каждого значения в выборку, а вероятность их появления в выборке. Красной линией мы нарисовали функцию распределения плотности вероятности значений времени доставки. Выше мы пытались экспериментальным путем определить какую долю составляют значения времени больше 40 минут. И данный график должен натолкнуть нас на мысль о том, что есть два способа сделать это. Первый - экспериментальный, т.е. мы моделируем, скажем, 5000 доставок, строим гистограмму и находим сумму высот прямоугольников, расположенных правее черной линии:
np.random.seed(42) N = 10000 values = np.trunc(norm_rv.rvs(N)) fig, ax = plt.subplots() v_le_41 = np.histogram(values, np.arange(9.5, 41.5)) v_ge_40 = np.histogram(values, np.arange(40.5, 51.5)) ax.bar(np.arange(10, 41), v_le_41[0]/N, color='0.8') ax.bar(np.arange(41, 51), v_ge_40[0]/N) p = np.sum(v_ge_40[0]/N) ax.set_title('P(Y>40min) = {:.3}'.format(p)) ax.vlines(40.5, 0, 0.08, color='k', lw=1);
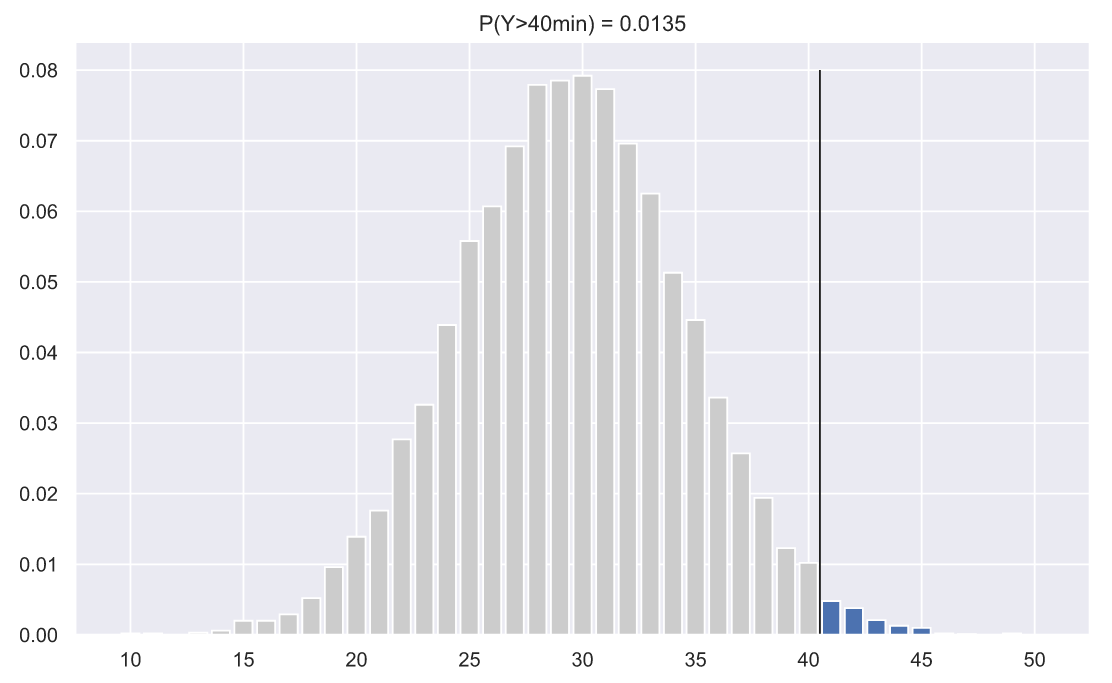
Второй путь - аналитический. Поскольку мы знаем, что значения доставки пиццы берутся из нормального распределения, то мы можем воспользоваться функцией распределения плотности вероятности нормального распределения. Функция распределения плотности хороша тем, что площадь под ней всегда равна единице и если нас интересует вероятность того, что величина примет значение большее или меньшее указанного, то достаточно найти площадь под функцией которая находится правее или левее этого значения. Например, вычислить и изобразить вероятность того, что время доставки будет диться более 40 минут можно так:
fig, ax = plt.subplots() x = np.linspace(norm_rv.ppf(0.0001), norm_rv.ppf(0.9999), 300) ax.plot(x, norm_rv.pdf(x)) ax.fill_between(x[x>41], norm_rv.pdf(x[x>41]), np.zeros(len(x[x>41]))) p = 1 - norm_rv.cdf(41) ax.set_title('P(Y>40min) = {:.3}'.format(p)) ax.hlines(0, 10, 50, lw=1, color='k') ax.vlines(41, 0, 0.08, color='k', lw=1);
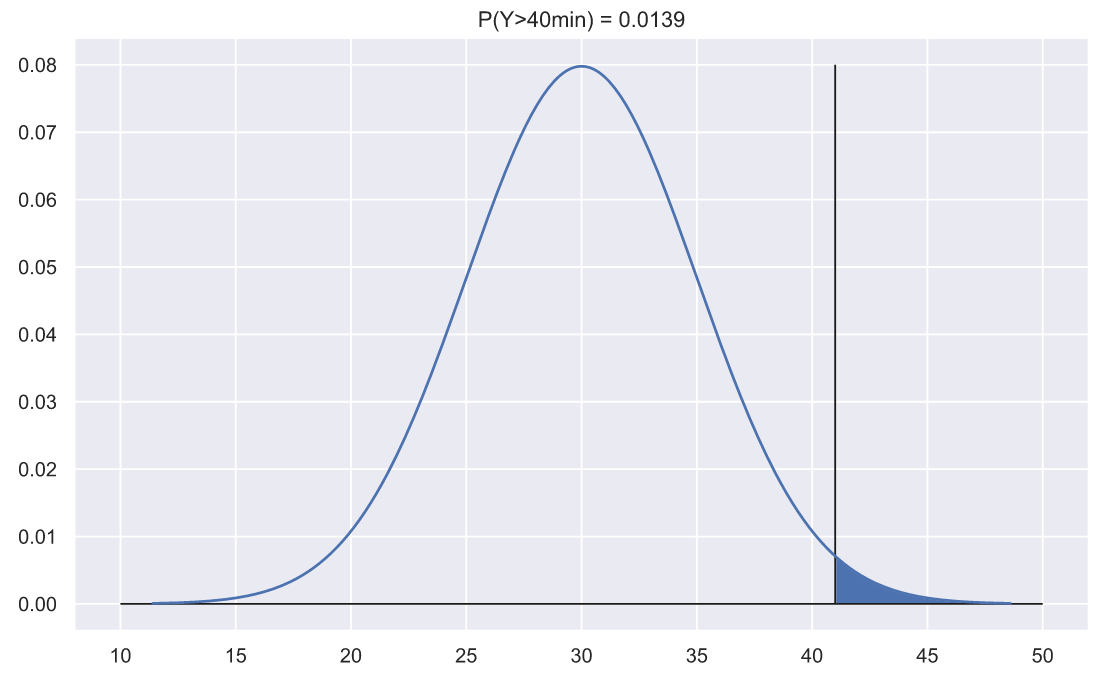
Значения вероятности в первом и втором случае получились довольно близкими. Но надо оговориться, что в первом случае мы использовали дискретную случайную величину, а во втором - непрерывную, поэтому код выглядит несколько "читерским", как буд-то бы все намеренно подгонялось так, что бы два результата были похожи. Конечно, возможно я что-то перемудрил, но вроде бы все верно. В первом случае мы считаем сколько раз доставка составляла более 40 минут, т.е. считали сколько доставок длились 41, 42, 43 и т.д. минут. Во втором случае мы просто считаем сколько непрерывных величин оказалось правее значения 41.0. В принципе, модуль SciPy позволяет создавать собственные распределения случайных переменных, в руководстве даже имеется пример, как создать дискретно-нормальное распределение. Но если задуматься, то наличие дискретных значений и использование непрерывных функций распределения, это своего рода - неизбежность, ведь подавляющее большинство измерений носит дискретный характер: рост, вес, доход и т.д. Так что далее мы не будем больше оговариваться по этому поводу, а лучше вернемся к Z-значениям.
Итак, допустим мы оказались в средиземье и каким-то образом выяснили что рост хобитов и гномов в сантиметрах распределен как и
. Если рост Фродо равен 99 сантиметрам а рост Гимли 143 сантиметра, то как понять чей рост более типичен среди своих народов? Что бы выяснить это мы можем изобразить функцию распределения плотности вероятности для каждого народа с отмеченными значениями, а заодно определить долю тех, кто превышает эти значения:
fig, ax = plt.subplots(nrows=1, ncols=2, figsize = (12, 5)) nrv_hobbit = stats.norm(91, 8) nrv_gnome = stats.norm(134, 6) for i, (func, h) in enumerate(zip((nrv_hobbit, nrv_gnome), (99, 143))): x = np.linspace(func.ppf(0.0001), func.ppf(0.9999), 300) ax[i].plot(x, func.pdf(x)) ax[i].fill_between(x[x>h], func.pdf(x[x>h]), np.zeros(len(x[x>h]))) p = 1 - func.cdf(h) ax[i].set_title('P(H > {} см) = {:.3}'.format(h, p)) ax[i].hlines(0, func.ppf(0.0001), func.ppf(0.9999), lw=1, color='k') ax[i].vlines(h, 0, func.pdf(h), color='k', lw=2) ax[i].set_ylim(0, 0.07) fig.suptitle('Хобиты слева, гномы справа', fontsize = 20);
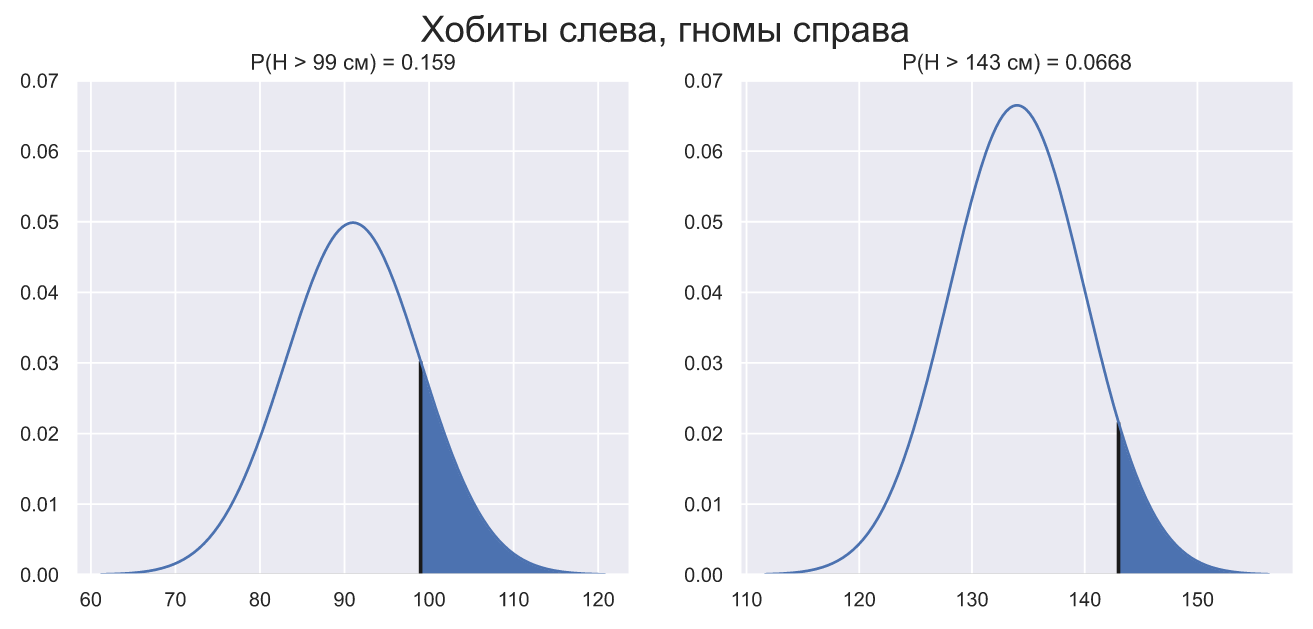
Эти графики, конечно не обладают свойством самоочевидности, но в принципе, можно сказать (и наверняка ошибиться), что рост Фродо несколько ближе к вершине распределения чем рост Гимли. А это значит, что вероятность встретить хобита с таким же ростом как у Фродо несколько больше вероятности встретить гнома с ростом как у Гимли. Именно это и понимается под словом "типичность".
Выполнить сравнение типичности гораздо проще и нагляднее если воспользоваться Z-значениями:
fig, ax = plt.subplots() N_rv = stats.norm() x = np.linspace(N_rv.ppf(0.0001), N_rv.ppf(0.9999), 300) ax.plot(x, N_rv.pdf(x)) ax.hlines(0, -4, 4, lw=1, color='k') ax.vlines(1, 0, 0.4, color='r', lw=2, label='Фродо') ax.vlines(1.5, 0, 0.4, color='g', lw=2, label='Гимли') ax.legend();
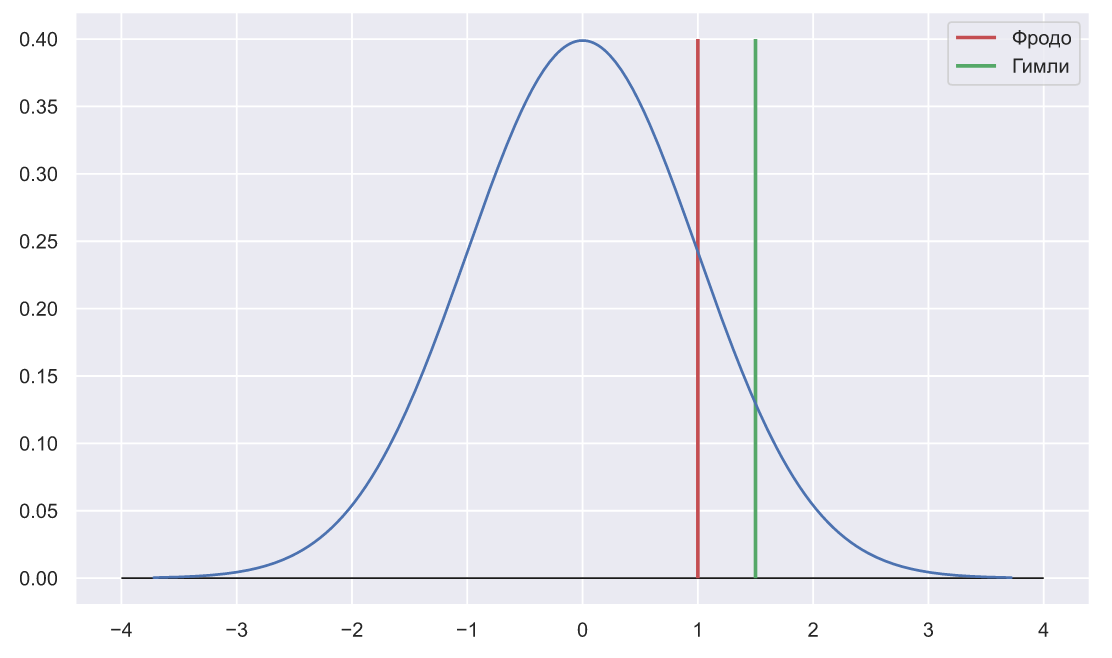
Огромным преимуществом Z-значений является то, что они "стандартизированы", т.е. преобразованы так словно они взяты из стандартного нормального распределения , именно поэтому два Z-значения нарисованы на фоне единственной кривой. Однако, в общем случае, даже само рисование графиков вовсе не обязательно, потому что меньшие по модулю Z-значения обладают большей частотой появления. Одной записи:
достаточно для того что бы понять, какое из значений находится ближе к вершине распределения и сделать соответствующие выводы.
Сравнение Z-значений нескольких величин из разных "нормальных" выборок с разными параметрами распределения возможно потому, что сами Z-значения измеряются в сигмах. Это становится более очевидным если еще раз взглянуть на знаменатель формулы:
Не важно, что вы пытаетесь сравнить: рост, вес, литры или доход; в чем бы не измерялись сравниваемые величины, после вычисления Z-значений они будут измеряться в сигмах. Чем меньше по модулю Z-значение, тем ближе оно к вершине распределения, а знак Z-значения укажет по какую сторону от вершины это значение находится.
Имеет смысл отметить, что с математически-строгой точки зрения вероятность получения какого-то конкретного значения из непрерывного распределения стремится к нулю. В таких случаях, всегда говорят о вероятности попадания этого значения в заданный интервал. Поэтому, когда мы говорим, что Z-значение какой-то величины позволяет оценить вероятность (частоту) ее пояления, то мы вовсе не выходим за границы здравого смысла. В реальном мире мы никогда не работаем с действительно непрерывными величинами. Да, мы можем измерять рост в нанометрах, а время в фемтосекундах, но это все равно будут дискретные значения. Распределение дискретных величин может хорошо приближаться распредилением величин непрерывных - нам этого достаточно.
Z-статистика
Теперь давайте снова вернемся к нашему соседу, который возмущен слишком долгой доставкой пиццы. Выше мы вычислили Z-значение для 40 минут:
Пока у нас нет опыта, достаточного для того что бы сразу понять много это или мало, лучше изображать эти значения графически:
fig, ax = plt.subplots() N_rv = stats.norm() x = np.linspace(N_rv.ppf(0.0001), N_rv.ppf(0.9999), 300) ax.plot(x, N_rv.pdf(x)) ax.hlines(0, -4, 4, lw=1, color='k') ax.vlines(2, 0, 0.4, color='g', lw=2);
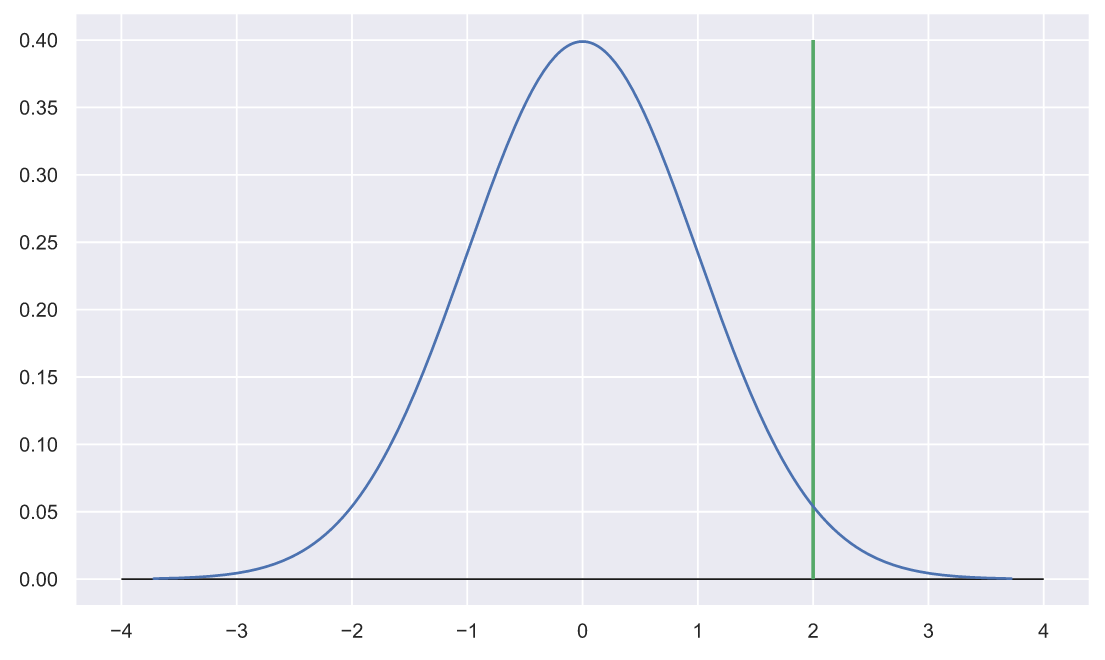
Это значение находится справа от вершины на расстоянии , что довольно много. Однако, сосед утверждает, что ждал пиццу больше сорока минут три дня подряд. Возможно он и не вычислял среднее время ожидания своей пиццы, но три значения - это уже статистика!
Характеристики генеральной совокупности называют параметрами, а характеристики выборки - статистиками. Замеряя время доставки на протяжении 365-и дней, мы сделали вывод о параметрах генеральной совокупности, т.е. времени всех возможных доставок пиццы, решив что эти значения берутся из . А зная распределение мы можем поэкспериментировать. Например, наш сосед сделал всего три заказа, и по его ощущениям среднее время доставки, было больше сорока минут. А что если мы повторим этот эксперимент 5000 раз и посмотрим на то как распределено среднее трех заказов:
sns.histplot(np.trunc(norm_rv.rvs(size=(N, 3))).mean(axis=1), bins=np.arange(19, 42));
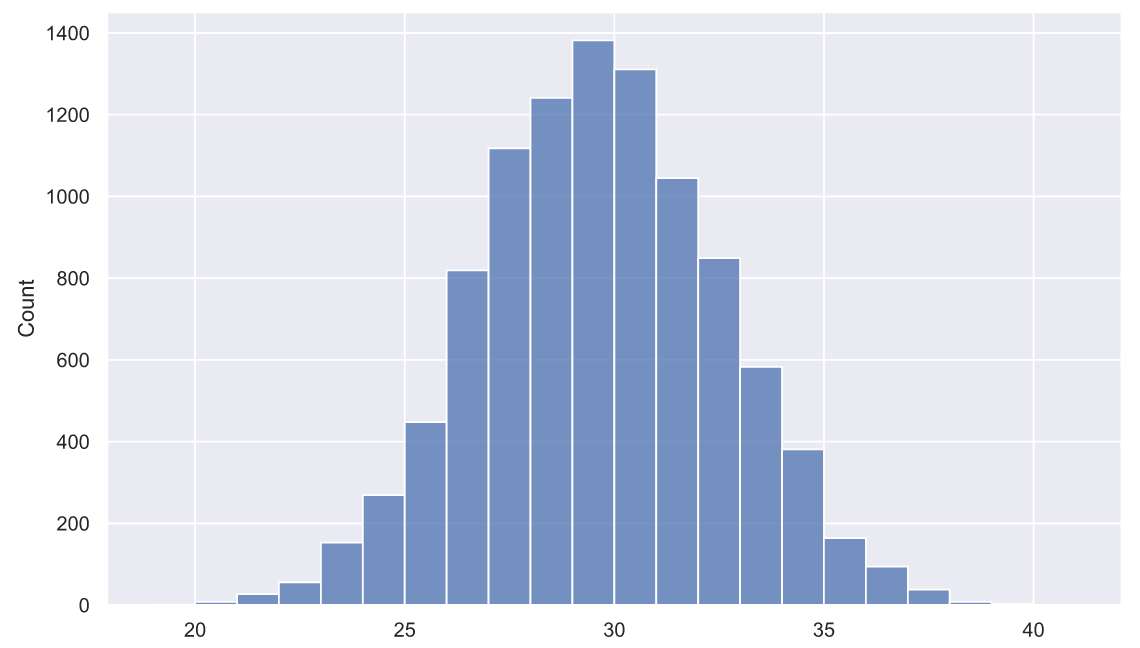
Судя по графику, получить среднее значение трех заказов большее 40 минут - практически нереально. И вот тут возможны два предположения:
либо сосед врет;
либо что-то с генеральной совокупностью, т.е. по какой-то причине, доставка и правда длится дольше обычного.
Вычисленное выше Z-значение для сорока минут (Z = 2), позволяет оценить долю (вероятность появления) значений больших сорока:
1 - N_rv.cdf(2)
0.02275013194817921
Поэтому не удивительно, что вероятность получить среднее время трех доставок большее 40 минут исчезающе мала:
(1 - N_rv.cdf(2))**3
1.1774751750476762e-05
Если каждое отдельное значение времени доставки мы можем оценить с помощью Z-значения, то для того что-бы оценить вероятность среднего арифметического этих значений нам нужно воспользоваться Z-статистикой:
где - это среднее значение для нашей выборки,
и
среднее значение и стандартное отклонение для генеральной совокупности, а
- размер выборки.
Давайте предположим что мы сделали три заказа и среднее значение оказалось равным 35 минутам, тогда Z-статистика будет вычисляться так:
Z-статистика, как и Z-значение является стандартизированной величиной и так же измеряется в сигмах, что позволяет использовать стандартное нормальное распределение для подсчета вероятностей. Фактически мы задаемся вопросом, а какова вероятность того, что среднее значение времени трех доставок попадет в промежуток
который в нашем случае выглядит как [25; 35] минут. Как и ранее мы можем найти данную вероятность с помощью моделирования:
N = 10000 means = np.trunc(norm_rv.rvs(size=(N, 3))).mean(axis=1) means[(means>=25)&(means<=35)].size/N
0.9241
N = 10000 fig, ax = plt.subplots() means = np.trunc(norm_rv.rvs(size=(N, 3))).mean(axis=1) h = np.histogram(means, np.arange(19, 41)) ax.bar(np.arange(20, 25), h[0][0:5]/N, color='0.5') ax.bar(np.arange(25, 36), h[0][5:16]/N) ax.bar(np.arange(36, 41), h[0][16:22]/N, color='0.5') p = np.sum(h[0][6:16]/N) ax.set_title('P(25min < Y < 35min) = {:.3}'.format(p)) ax.vlines([24.5 ,35.5], 0, 0.08, color='k', lw=1);
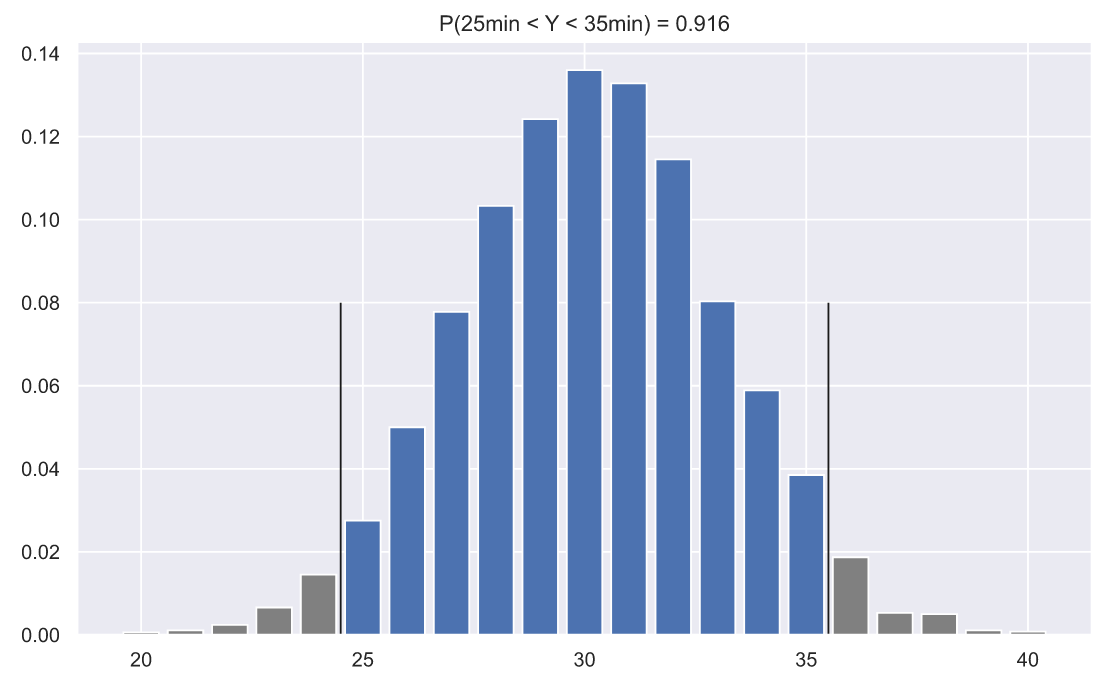
С другой стороны, мы можем вычислить ту же вероятность аналитическим способом:
x, n, mu, sigma = 35, 3, 30, 5 z = abs((x - mu)/(sigma/n**0.5)) N_rv = stats.norm() fig, ax = plt.subplots() x = np.linspace(N_rv.ppf(0.0001), N_rv.ppf(0.9999), 300) ax.plot(x, N_rv.pdf(x)) ax.hlines(0, x.min(), x.max(), lw=1, color='k') ax.vlines([-z, z], 0, 0.4, color='g', lw=2) x_z = x[(x>-z) & (x<z)] # & (x<z) ax.fill_between(x_z, N_rv.pdf(x_z), np.zeros(len(x_z)), alpha=0.3) p = N_rv.cdf(z) - N_rv.cdf(-z) ax.set_title('P({:.3} < z < {:.3}) = {:.3}'.format(-z, z, p));
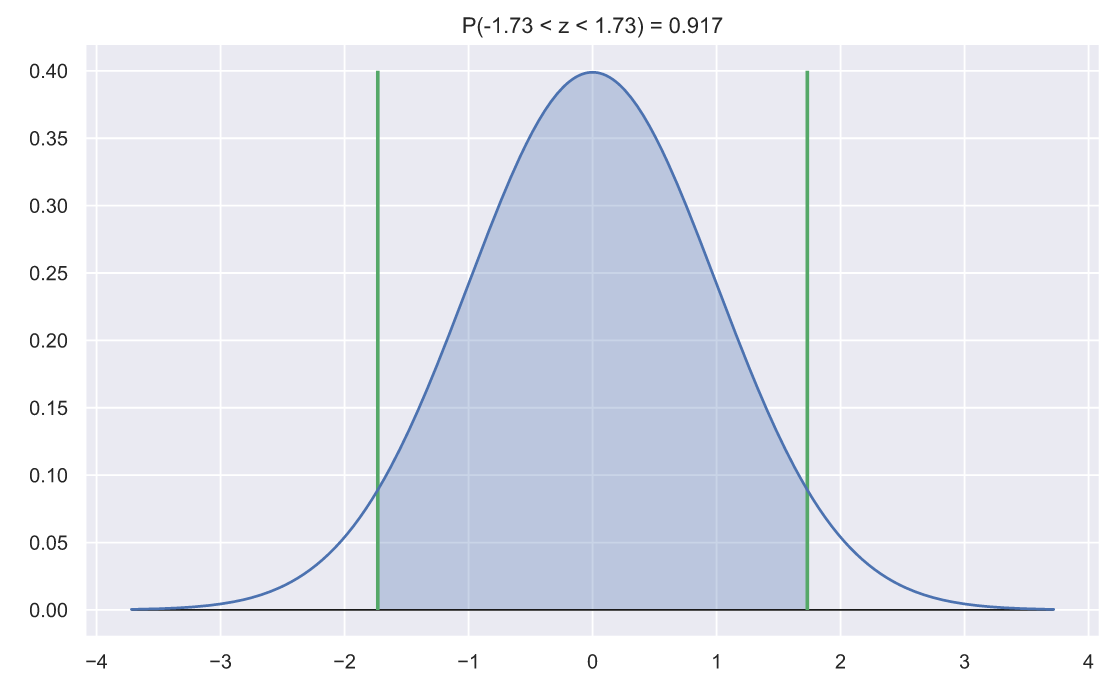
Обратите внимание, на то что Z-статистика зависит как от среднего выборки - , так и от величины выборки -
. Если мы закажем пиццу 5, 30 или 100 раз, то какова вероятность того, что среднее значение времени доставок окажется в интервале [29; 31]? Давайте взглянем:
fig, ax = plt.subplots(nrows=1, ncols=3, figsize = (12, 4)) for i, n in enumerate([5, 30, 100]): x, mu, sigma = 31, 30, 5 z = abs((x - mu)/(sigma/n**0.5)) N_rv = stats.norm() x = np.linspace(N_rv.ppf(0.0001), N_rv.ppf(0.9999), 300) ax[i].plot(x, N_rv.pdf(x)) ax[i].hlines(0, x.min(), x.max(), lw=1, color='k') ax[i].vlines([-z, z], 0, 0.4, color='g', lw=2) x_z = x[(x>-z) & (x<z)] # & (x<z) ax[i].fill_between(x_z, N_rv.pdf(x_z), np.zeros(len(x_z)), alpha=0.3) p = N_rv.cdf(z) - N_rv.cdf(-z) ax[i].set_title('n = {}, z = {:.3}, p = {:.3}'.format(n, z, p)); fig.suptitle(r'Z-статистики для $\bar{x} = 31$', fontsize = 20, y=1.02);
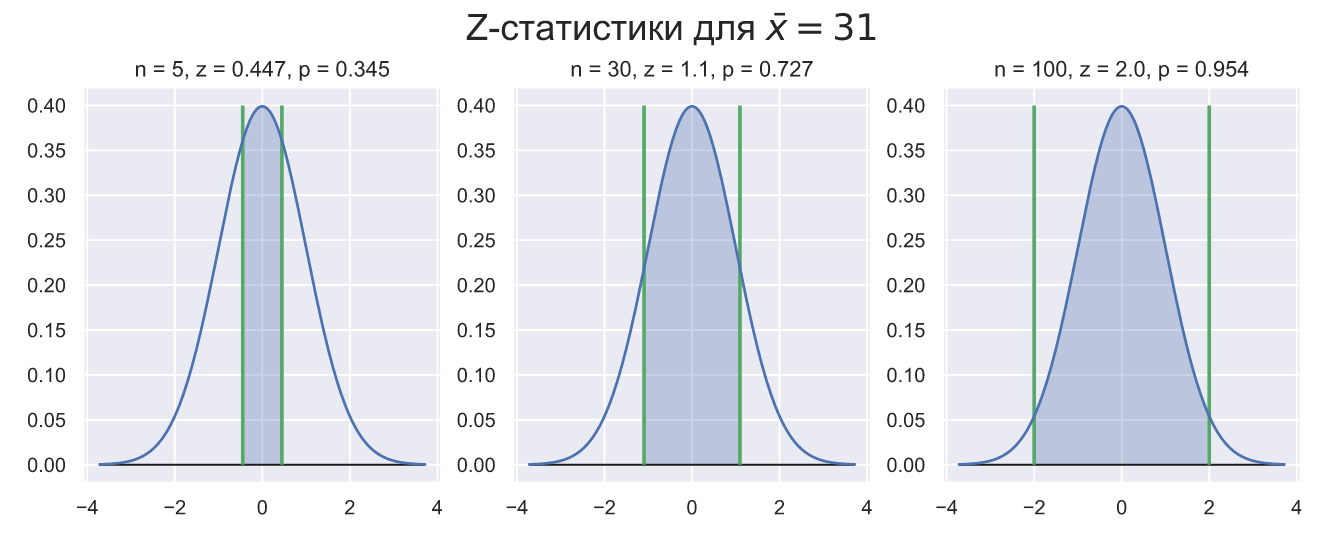
При 5 заказах среднее выборки попадает в интервал [29;31] скорее случайно, чем систематически. При 30 заказх около четверти средних значений так и не войдут в заданный интервал. И только при сотне заказов мы можем быть более-менее уверены в том что отклонение среднего выборки от среднего генеральной совокупности не будет больше 1 минуты.
С другой стороны, мы можем рассуждать и по другому: если среднее генеральной совокупности равно 30 минутам, то какова вероятность получить среднее выборки равное 31 минуте если мы сделаем 5, 30 или 100 заказов? Очевидно, что при n=5 среднее выборки, может отклоняться очень сильно, следовательно, вероятность получить минуте очень высока. Но при
среднее выборки практически не отклоняется от среднего генеральной совокупности, поэтому получить случайным образом
при
практически невозможно. Что это значит? А это значит, что если мы сделали 100 заказов и получили среднее время доставки равное 31 минуте, то скорее всего мы ошибаемся насчет того, что среднее генеральной совокупности равно 30 минутам.
Но как быть с нашим соседом, ведь он сделал всего 3 заказа? Неужели он действительно прав? Судя по всему - да. Даже если среднее время ожидания составило 40 минут, то Z-статистика будет равна 3.81, а площадь под кривой будет практически равна 1:
x, n, mu, sigma = 41, 3, 30, 5 z = abs((x - mu)/(sigma/3**0.5)) N_rv = stats.norm() fig, ax = plt.subplots() x = np.linspace(N_rv.ppf(1e-5), N_rv.ppf(1-1e-5), 300) ax.plot(x, N_rv.pdf(x)) ax.hlines(0, x.min(), x.max(), lw=1, color='k') ax.vlines([-z, z], 0, 0.4, color='g', lw=2) x_z = x[(x>-z) & (x<z)] # & (x<z) ax.fill_between(x_z, N_rv.pdf(x_z), np.zeros(len(x_z)), alpha=0.3) p = N_rv.cdf(z) - N_rv.cdf(-z) ax.set_title('P({:.3} < z < {:.3}) = {:.3}'.format(-z, z, p));

В свою очередь, это значит, что вероятность случайного отклонения среднего выборки из трех значений, взятых из генеральной совокупности с и
более чем на 10 минут исчезающе мала. В этом случае мы можем заключить только следующее:
либо наш сосед просто чрезвычайно "везучий" человек;
либо доставка пиццы и вправду теперь выполняется дольше обычного.
Что из этих пунктов является наиболее вероятным? Скорее всего сосед прав насчет долгой доставки.
p-value
Мы смогли убедиться в том что Z-статистика позволяет оценить вероятность того, что среднее выборки размером
, взятой из генеральной совокупности попадет в заданный интервал значений. Это удобно тем, что позволяет сделать вывод о случайности полученного
. Чем меньше модуль значения Z-статистики, тем меньше достоверность среднего. Например выше мы видели, что вероятность попадания
при
в интервал [29;31] составляет всего около 0.35. В то время как вероятность непопадания в заданный интервал равна 1−0.35=0.65. Поэтому мы и сделали вывод о том, что значение
при
скорее обусловлено случайностью, чем какими-то объективными причинами.
Фактически, значение вероятности 0.65, полученное выше - это и есть то самое p-value которое как раз и показывает вероятность случайного выхода за границы интервала, задаваемого значением Z-статистики, что можно изобразить следующим образом:
x, n, mu, sigma = 31, 5, 30, 5 z = abs((x - mu)/(sigma/n**0.5)) N_rv = stats.norm() fig, ax = plt.subplots() x = np.linspace(N_rv.ppf(0.0001), N_rv.ppf(0.9999), 300) ax.plot(x, N_rv.pdf(x)) ax.hlines(0, x.min(), x.max(), lw=1, color='k') ax.vlines([-z, z], 0, 0.4, color='g', lw=2) x_le_z, x_ge_z = x[x<-z], x[x>z] ax.fill_between(x_le_z, N_rv.pdf(x_le_z), np.zeros(len(x_le_z)), alpha=0.3, color='b') ax.fill_between(x_ge_z, N_rv.pdf(x_ge_z), np.zeros(len(x_ge_z)), alpha=0.3, color='b') p = N_rv.cdf(z) - N_rv.cdf(-z) ax.set_title('P({:.3} < z < {:.3}) = {:.3}'.format(-z, z, p));
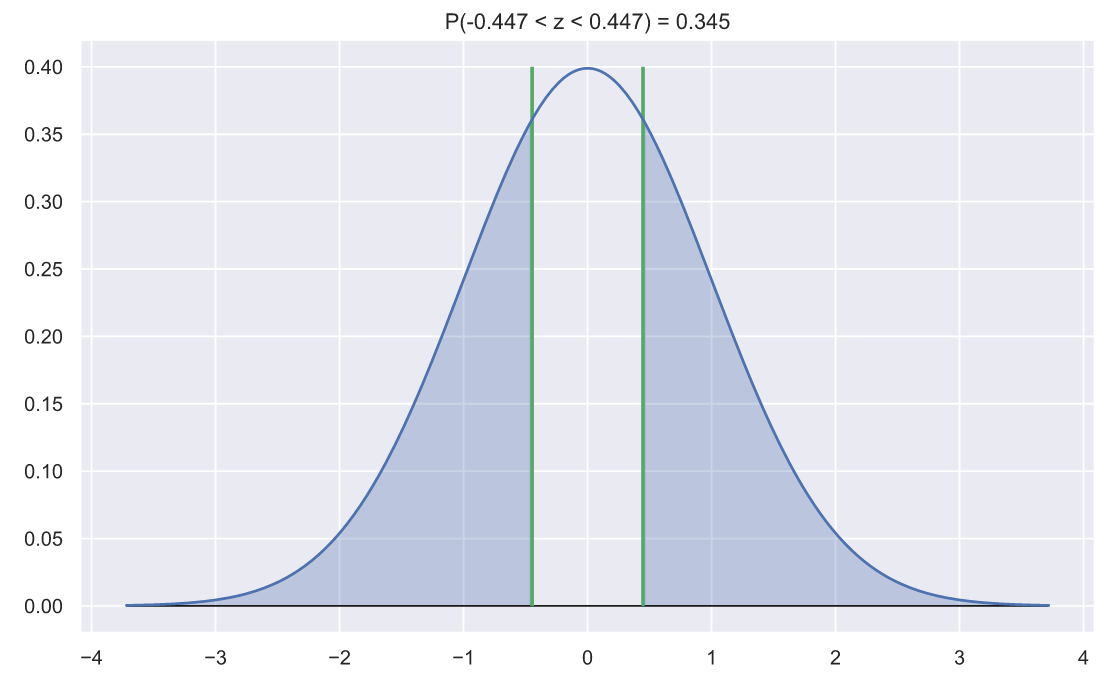
Чем меньше p-value тем меньше вероятность того, что среднее выборки получено случайно. При этом p-value напрямую связано с двусторонними гипотезами, т.е. гипотезами о попадании величины в заданный интервал. Если мы получили какие-то результаты, но p-value оказалось довольно большим, то вряд ли эти результаты могут считаться значимыми. Причем, традиционно, уровень значимости, обозначаемый буквой равен 0.05, а это означает, что для подтверждения значимости результатов p-value должно быть меньше этого уровня. Однако, стоит обязательно отметить, что традиционный уровень значимости
может быть непригоден в некоторых областях исследований. Например, в сфере образования наверняка можно обойтись
, а вот в квантовой физике, запросто придется снизить этот уровень до 5 сигм, т.е.
будет равна:
1 - (N_rv.cdf(5) - N_rv.cdf(-5))
5.733031438470704e-07
Так же не следует забывать о том, что значимость может зависить как от среднего выборки, так и от ее размера. Если вы получили несколько значений, крайне не характерных для генеральной совокупности, как в случае с нашим соседом, то это уже повод насторожиться. Например, если наш сосед так же как и мы измерял время с помощь стенных часов, то получить большие значения времени он мог из-за "севшей" батарейки. Ошибки, связанные с извлечением выборки (сбором данных) весьма распространены. Если никаких ошибок нет, то для пущей уверенности достаточно еще немного увеличить выборку. Например, наш сосед, мог бы сделать еще два заказа, и только после этого начать скандалить.
С другой стороны, что бы подтвердить небольшие отклонения от среднего генеральной совокупности, придется очень сильно увеличивать размер выборки. Так, например, если мы хотим заявить с уровнем значимости , что среднее время доставки пиццы равно 31 минуте, а не 30 как считалось ранее, то придется сделать не менее 100 заказов.
Напоследок
Кстати, я совсем забыл сказать, что Z-статистика основана на центральной предельной теореме: вне зависимости от того как распределена генеральная совокупность, распределение средних значений выборок будет стремиться к нормальному распределению, тем сильнее, чем больше размер выборок.
Это кажется не очень правдоподобным, но давайте взглянем. Сгенерируем 1000 значений из равномерного, экспоненциального и Лапласова распределения, а затем, последовательно, для каждого распределения построим kde-графики распределений среднего значения выборок разного размера:
Код для гифки
import matplotlib.animation as animation fig, axes = plt.subplots(nrows=2, ncols=3, figsize = (12, 7)) unif_rv = stats.uniform(loc=10, scale=10) exp_rv = stats.expon(loc=10, scale=1.5) lapl_rv = stats.laplace(loc=15) np.random.seed(42) unif_data = unif_rv.rvs(size=1000) exp_data = exp_rv.rvs(size = 1000) lapl_data = lapl_rv.rvs(size=1000) title = ['Uniform', 'Exponential', 'Laplace'] data = [unif_data, exp_data, lapl_data] y_max = [60, 310, 310] n = [3, 10, 30, 50] for i, ax in enumerate(axes[0]): sns.histplot(data[i], bins=20, alpha=0.4, ax=ax) ax.vlines(data[i].mean(), 0, y_max[i], color='r') ax.set_xlim(10, 20) ax.set_title(title[i]) def animate(i): for ax in axes[1]: ax.clear() for j in range(3): rand_idx = np.random.randint(0, 1000, size=(1000, n[i])) means = data[j][rand_idx].mean(axis=1) sns.kdeplot(means, ax=axes[1][j]) axes[1][j].vlines(means.mean(), 0, 2, color='r') axes[1][j].set_xlim(10, 20) axes[1][j].set_ylim(0, 2.1) axes[1][j].set_title('n = ' + str(n[i])) fig.set_figwidth(15) fig.set_figheight(8) return axes[1][0], axes[1][1],axes[1][2] dist_animation = animation.FuncAnimation(fig, animate, frames=np.arange(4), interval = 200, repeat = False) # Сохраняем анимацию в виде gif файла: dist_animation.save('dist_means.gif', writer='imagemagick', fps=1)
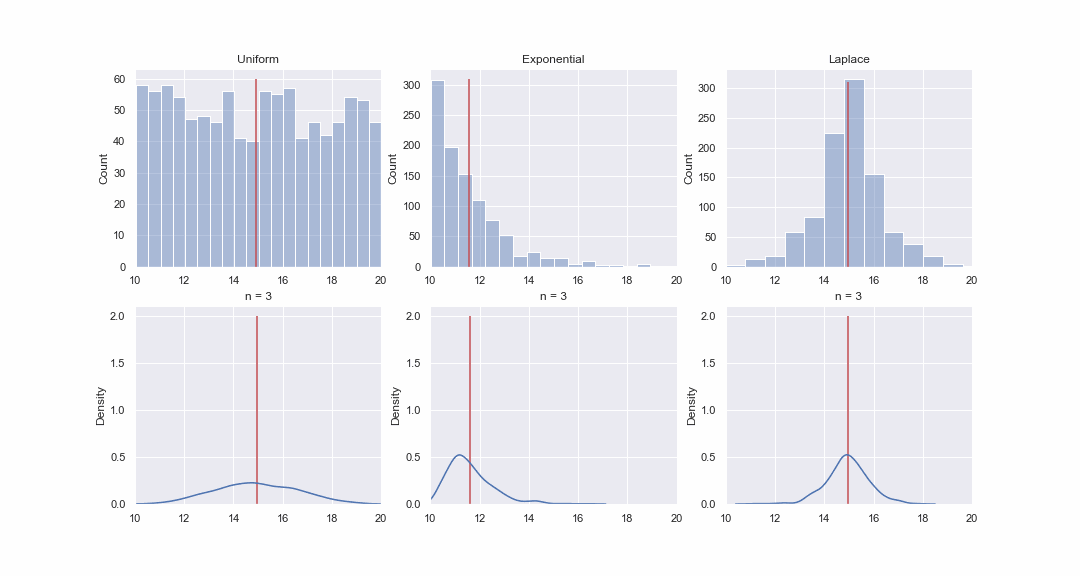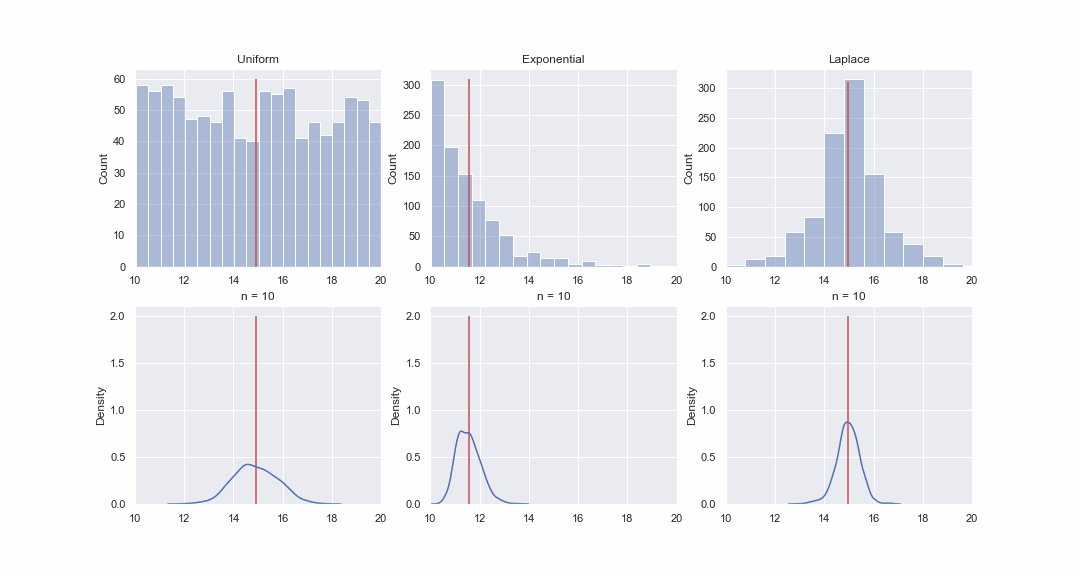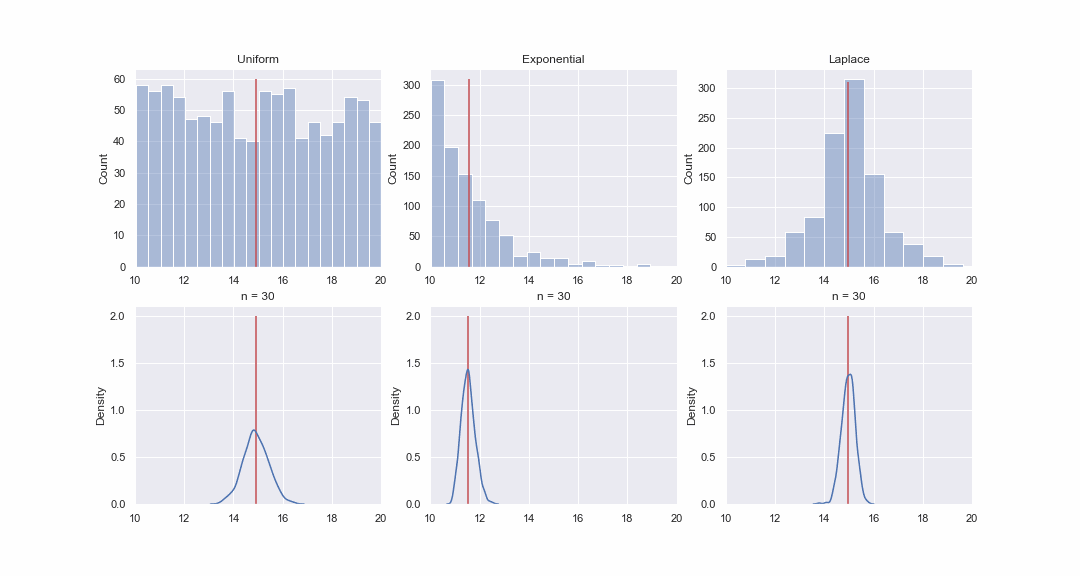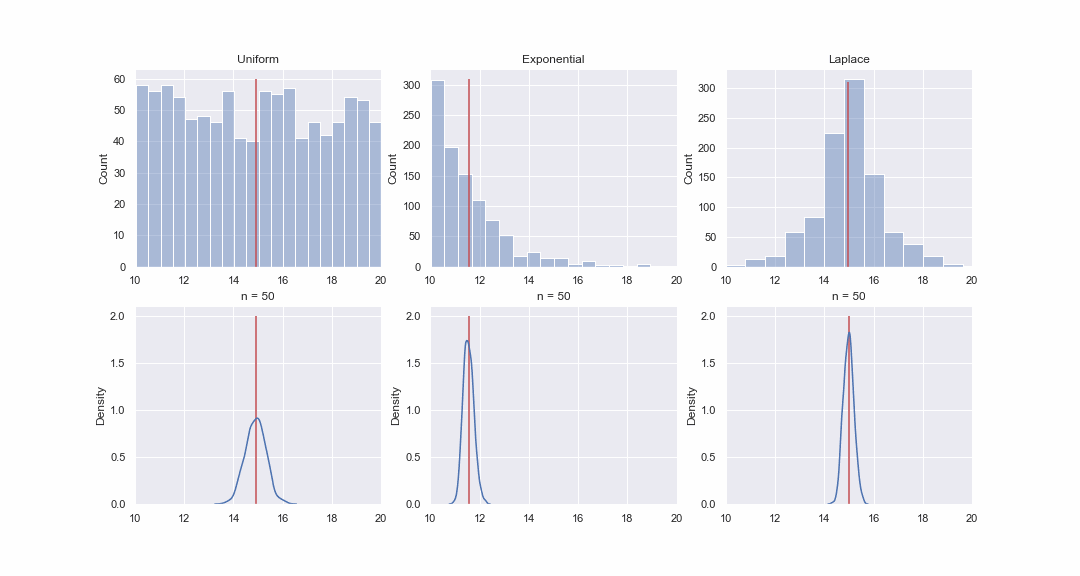
Конечно, картинка - это вовсе не доказательство, но если хотите, то можете провести тесты на нормальность самостоятельно. Впрочем, в следующей статье мы как раз займемся тестами и доказательством гипотез.
В общем, спасибо за внимание. Жму F5 и жду ваших и комментариев.
