PatientZero 16 сен 2021 в 10:58

Рейкастинг в игровых 2D-движках

8 мин

15K

Работа с 3D-графикой*Разработка игр*Алгоритмы*

Перевод

Автор оригинала: Sebastian Szczepański

Введение

На мой взгляд, рейкастинг — великолепная концепция, понять которую не так сложно, но качественных ресурсов по ней очень мало. Я расскажу о математике, лежащей в её основе, чтобы вы при желании с лёгкостью могли реализовать её в своих будущих проектах. Постараюсь сделать объяснение как можно более понятным, рассказать о всех тонкостях и проблемах, с которыми вы можете столкнуться. Также мы поговорим об оптимизации и о том, как сильно вам могут помочь пространственные хэш-карты. Ещё я напишу простые интерактивные примеры, с которыми вы сможете поэкспериментировать. Учтите, что демо написаны максимально простым образом, не ожидайте увидеть в них код уровня энтерпрайза — мы изучаем саму концепцию, а не реализацию.

Что такое рейкастинг?

«Рейкастинг (ray casting, „испускание лучей“) — самый простой из множества алгоритмов рендеринга компьютерной графики, использующих геометрический алгоритм трассировки лучей (ray tracing). Алгоритмы рендеринга на основе трассировки лучей работают на уровне изображений, выполняя рендеринг трёхмерных сцен в двухмерные изображения…

Принцип рейкастинга заключается в том, чтобы попиксельно отслеживать испускаемые из глаза лучи, чтобы найти ближайший объект, препятствующий пути каждого луча — представьте, что изображение — это проволочная сетка, а каждый квадрат сетки — это пиксель. Таким образом мы можем определить объект, который видит глаз через этот пиксель.» — Википедия

Ну, звучит не очень понятно, правда? Давайте упростим объяснение. Рейкастинг — это популярная фундаментальная техника, используемая для определения видимости определённых объектов (полигонов) трассировкой лучей из глаза (например, персонажа игрока) до каждого пикселя (ну, в нашем случае это не совсем так, но подробнее об этом позже) и нахождением самых ближайших пересечений с объектами.

Где может использоваться рейкастинг?

Рейкастинг можно использовать по-разному, особенно в трёхмерном пространстве. Я выделю три наиболее важных по моему мнению применения, часто встречающихся в игровых 2D-движках:

Создание 3D-перспективы на 2D-карте

Самой известной игрой, использующей эту технику, является Wolfenstein 3D. Лучи в ней трассировались для определения ближайших объектов, а их расстояние от позиции игрока использовалось для правильного масштабирования.

Простой рейкастинг с коррекцией фишай Лукаса Виейра

Задача точки в многоугольнике

Задача PIP (point-in-polygon) заключается в определении того, находится ли точка внутри, снаружи или на границе многоугольника. При помощи алгоритма рейкастинга мы можем посчитать, сколько раз точка пересекает края многоугольника. Если количество пересечений чётно, то точка находится снаружи многоугольника. Если количество пересечений нечётно, то точка находится внутри или на границе многоугольника.

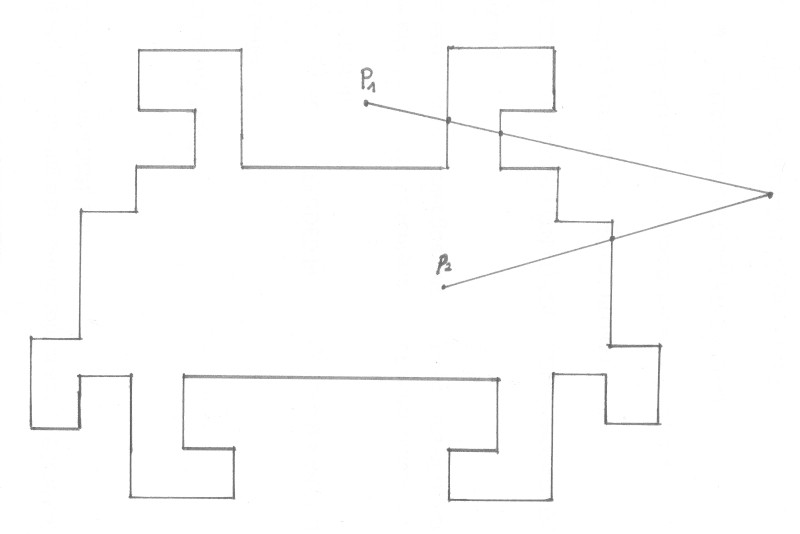
Решение задачи точки в многоугольнике при помощи рейкастинга

Видимость объектов и испускание света

В статье мы рассмотрим именно эту задачу — определение видимости объектов для игрока и освещение видимой области.

Видимость объектов и испускание света

Видимость объектов и испускание света в 2D-играх

В этом разделе мы рассмотрим такие базовые понятия, как точки пересечения, испускание лучей, сортировка точек пересечения для освещения видимой области, а также несколько слов скажем о кругах. На каждом из этапов я буду писать интерактивные демо, чтобы вы не запутались и могли сразу же увидеть результаты.

Точка пересечения отрезка и луча

Здесь мы поговорим о точках пересечения. Давайте поэтапно разберёмся, как их находить и использовать. Сначала мы выведем параметрическое уравнение прямой, вычислим точки пересечения, а затем узнаем, как эффективно определять ближайшую из них.

Вывод параметрического уравнения прямой

Давайте сначала поговорим о прямых и их параметрическом уравнении.

Пример прямой линии

Мы можем выразить вектор $\overrightarrow{AP}$ следующим уравнением: $\overrightarrow{AP} = t\overrightarrow{AB}$ , где $inline$ — параметр уравнения, определяющий, насколько мы растягиваем $inline$ или сжимаем $inline$ , и меняем ли мы направление $inline$ вектора $\overrightarrow{AP}$ относительно вектора $\overrightarrow{AB}$ .

Позвольте продемонстрировать пару примеров:

Пример параметров параметрического уравнения прямой

Как вы могли заметить, мы можем использовать $inline$ как коэффициент масштабирования: $inline$ . Мы воспользуемся этим при определении ближайшей точки пересечения.

Теперь мы можем легко увидеть, нужно ли нам, чтобы точка находилась на:

прямой: $t \in \mathbb{R}$ ,
луче: $t \geq 0$ ,
отрезке прямой: $0 \leq t \leq 1$ .

Выяснив всё это, мы наконец можем вывести параметрическое уравнение:

$\begin{align} \overrightarrow{AP} &= t \overrightarrow{AB} \\ P - A &= t (B - A) \\ P &= t(B - A) + A \\ \end{align}$

Если вы всё ещё не понимаете, что здесь происходит, то рекомендую вам прочитать потрясающую короткую лекцию Норма Прокупа: Parametrizing a Line Segment — Concept.

Вычисление точки пересечения

Допустим, точка $inline$ является точкой пересечения отрезка прямой, заданного точками $inline$ и $inline$ , и луча, заданного точками $inline$ и $inline$ . Тогда точку $inline$ можно выразить как систему из двух уравнений:

$\left\{\begin{align} P &= s(B - A) + A\text {, where } 0 \leq s \leq 1 \text{, and} \\ P &= r(D - C) + C\text {, where } r \geq 0 \text{.} \end{align}\right.$

Вычислим $inline$ и $inline$ :

$\begin{align} s(B_x - A_x) + A_x &= r(D_x - C_x) + C_x \Rightarrow s = \tfrac{r(D_x - C_x) + (C_x - A_x)}{B_x - A_x} \\ s(B_y - A_y) + A_y &= r(D_y - C_y) + C_y \Rightarrow r = \tfrac{s(B_y - A_y) + (A_y - C_y)}{D_y - C_y} \end{align}$

.
Подставим $inline$ во второе уравнение:

$\begin{align} &\tfrac{r(D_x - C_x) + (C_x - A_x)}{B_x - A_x} (B_y - A_y) + A_y = r(D_y - C_y) + C_y \\[10pt] &r \tfrac{(D_x - C_x)(B_y - A_y)}{B_x - A_x} + \tfrac{(C_x - A_x)(B_y - A_y)}{B_x - A_x} + A_y = r(D_y - C_y) + C_y \\[10pt] &r (\tfrac{(D_x - C_x)(B_y - A_y)}{B_x - A_x} - (D_y - C_y)) = (C_y - A_y) - \tfrac{(C_x - A_x)(B_y - A_y)}{B_x - A_x} \\[10pt] &r \tfrac{(D_x - C_x)(B_y - A_y) - (D_y - C_y)(B_x - A_x)}{B_x - A_x} = \tfrac{(C_y - A_y)(B_x - A_x) - (C_x - A_x)(B_y - A_y)}{B_x - A_x} \\[10pt] &r = \tfrac{(C_y - A_y)(B_x - A_x) - (C_x - A_x)(B_y - A_y)}{(D_x - C_x)(B_y - A_y) - (D_y - C_y)(B_x - A_x)} \\[10pt] &r = \tfrac{(B_x - A_x)(C_y - A_y) - (C_x - A_x)(B_y - A_y)}{(D_x - C_x)(B_y - A_y) - (B_x - A_x)(D_y - C_y)} \\[10pt] \end{align}$

Подставим $inline$ в первое уравнение:

$\begin{align} &s(B_x - A_x) + A_x = \tfrac{s(B_y - A_y) + (A_y - C_y)}{D_y - C_y} (D_x - C_x) + C_x \\[10pt] &s(B_x - A_x) + A_x = s \tfrac{(B_y - A_y)(D_x - C_x)}{D_y - C_y} + \tfrac{(A_y - C_y)(D_x - C_x)}{D_y - C_y} + C_x \\[10pt] &s (\tfrac{(B_y - A_y)(D_x - C_x)}{D_y - C_y} - (B_x - A_x)) = (A_x - C_x) - \tfrac{(A_y - C_y)(D_x - C_x)}{D_y - C_y} \\[10pt] &s \tfrac{(B_y - A_y)(D_x - C_x) - (B_x - A_x)(D_y - C_y)}{D_y - C_y} = \tfrac{(A_x - C_x)(D_y - C_y) - (A_y - C_y)(D_x - C_x)}{D_y - C_y} \\[10pt] &s = \tfrac{(A_x - C_x)(D_y - C_y) - (A_y - C_y)(D_x - C_x)}{(B_y - A_y)(D_x - C_x) - (B_x - A_x)(D_y - C_y)} \\[10pt] &s = \tfrac{(A_x - C_x)(D_y - C_y) - (D_x - C_x)(A_y - C_y)}{(D_x - C_x)(B_y - A_y) - (B_x - A_x)(D_y - C_y)} \\[10pt] \end{align}$

Вычислив $inline$ и $inline$ , мы можем вычислить $inline$ при помощи одного из уравнений системы.

Демо 1 — все точки пересечения

[Прим. пер.: в оригинале статьи все демо интерактивны.]

Поиск ближайшей точки пересечения

Для правильной отрисовки видимой области нам нужна только ближайшая точка пересечения. Наивным решением было бы вычисление расстояний между точкой начала луча и точками пересечения при помощи теоремы Пифагора: $\sqrt{(C_x - P_x) ^ 2 + (C_y - P_y) ^ 2}$ . Но вы помните о параметре уравнения прямой? Я уже говорил, что мы можем использовать его как коэффициент масштабирования. Так как мы хотим сравнить расстояния на луче, то можем найти наименьшее значение параметра $inline$ : $|\overrightarrow{CP_1}| < |\overrightarrow{CP_2}| \Leftrightarrow |r_1| < |r_2|$ .

Демо 2 — ближайшая точка пересечения

Испускание лучей

В этом разделе мы рассмотрим два способа испускания лучей. Мы сравним их и расскажем об их достоинствах и недостатках.

Испускание лучей по углу смещения

Первый способ — это испускание лучей во всех направлениях с заданным углом смещения. Например, мы можем испустить 30 лучей, смещённых на $12^\circ$ . Давайте сначала узнаем, как сгенерировать все эти лучи.

Пусть $inline$ будет начальной точкой всех лучей, а $inline$ — некой точкой на прямой, проходящей через $inline$ под углом $\phi$ :

Линия из заданной точки под неким углом

Мы можем задать $inline$ как $inline$ , а $inline$ как $inline$ (наша ось Y перевёрнута, отсюда и минус).

Теперь нам нужно вывести формулы для $inline$ и $inline$ :

$\left\{\begin{align} \sin(\phi) &= \tfrac{dy}{\mathit{dist}} \Rightarrow dy = \mathit{dist} * \sin(\phi) \\ \cos(\phi) &= \tfrac{dx}{\mathit{dist}} \Rightarrow dx = \mathit{dist} * \cos(\phi) \end{align}\right.$

В нашем случае $\mathit{dist}$ — это произвольное значение больше нуля (мы ищем любую точку на прямой), поэтому для упрощения вычислений вполне можно допустить, что $\mathit{dist} = 1$ . С учётом всего этого $P_2 = (x_1 + \sin(\phi), y_1 - \cos(\phi))$ , где $\phi$ — это угловое смещение.

Демо 3 — испускание лучей на угол смещения

Испускание лучей в вершины

Вероятнее всего, вам больше подойдёт испускание лучей в вершины. Вместо испускания лучей во всех направлениях мы просто можем испускать их в вершины многоугольников. Если количество вершин невелико, мы можем сэкономить вычислительные ресурсы, не испуская бесполезные лучи. В следующих разделах мы увидим, как это влияет на плавность анимаций, а также узнаем, как оптимизировать весь процесс.

Демо 4 — испускание лучей в вершины

Освещение видимой области

Сейчас начинается самое интересное. Мы осветим видимую область заливкой огромного многоугольника.

Сортировка точек пересечения

Чтобы создать правильный порядок вершин для построения многоугольника, нужно сначала отсортировать их по углу. Для этого мы используем функцию $inline$ . Подробнее о ней можно прочитать здесь.

Давайте сравним оба способа испускания лучей:

Демо 5 — испускание лучей с углами смещения (заполненная видимая область)

Демо 6 — испускание лучей в вершины (заполненная видимая область)

Оба способа выглядят ошибочными, скачущими и неточными. Давайте разберёмся, почему.

Испускание лучей с небольшим смещением

Заметьте, что происходит, когда лучи испускаются непосредственно на вершины — они должны идти дальше этой вершины, но мы получаем только ближайшую точку пересечения:

Проблема лучей на вершинах

Самым популярным решением является испускание двух дополнительных лучей со смещением на небольшой угол (в обоих направлениях) для каждого испущенного луча. Рассмотрим луч $inline$ , начинающийся в $inline$ и проходящий через $inline$ . Нам нужна такая точка $inline$ , чтобы луч $inline$ был повёрнут на $\phi$ с начальной точкой $inline$ . $inline$ будет иметь следующие координаты:

$\{\begin{align} C_x &= (B_x - A_x)\cos(\phi) - (B_y - A_y)\sin(\phi) + A_x \\ C_y &= (B_y - A_y)\cos(\phi) + (B_x - A_x)\sin(\phi) + A_y \end{align}$

Обратите внимание, что для первого способа это делать не нужно — мы просто прибавляем или вычитаем смещение из угла, который вычисляем. Дополнительные объяснения можно прочитать в этой статье.

Проблема лучей в вершинах решена

Давайте посмотрим, как ведёт себя освещение после этих изменений:

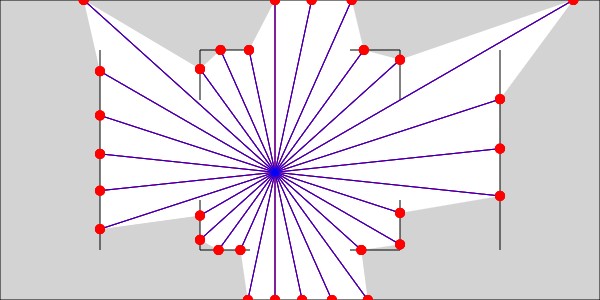
Демо 7 — испускание лучей с углом смещения (заполненная видимая область с дополнительными лучами)

Демо 8 — испускание лучей в вершины (заполненная видимая область с дополнительными лучами)

В случае первого способа это не особо улучшило ситуацию. Мы можем уменьшить смещение углов (увеличив количество лучей), но результат всё равно будет плохим. С другой стороны, второй способ выглядит очень плавным и точным. Далее мы больше не будем говорить о первом способе.

Круг видимости и фонарик

Иногда нам бывает нужно ограничивать видимость для игрока. Этого можно достичь, создав область усечения нужной формы. В показанных ниже демо я использовал метод CanvasRenderingContext2D.clip().

Демо 9 — круг видимости

Демо 10 — фонарик

Как вы могли заметить, это не является оптимизацией — мы всё равно вычисляем все точки пересечения. Мы вернёмся к этому после того, как узнаем о пространственных хэш-картах.

А как насчёт окружностей?

Я редко видел случаи испускания лучей на окружности. Считайте этот раздел дополнением, в котором я вкратце о них упомяну. Я покажу уравнения и простые демо, а дальнейшую работу оставлю вам.

Точка пересечения окружности и луча

Пусть $inline$ будет точкой пересечения, $inline$ — начальной точкой луча, $inline$ — точкой на луче, $inline$ — точкой центра окружности, а $inline$ — её радиусом.

$\left\{\begin{align} P_x &= t(B_x - A_x) + A_x \\ P_y &= t(B_y - A_y) + A_y \\ r ^ 2 &= (P_x - C_x) ^ 2 + (P_y - C_y) ^ 2 \end{align}\right.$

Решаем относительно $inline$ :

$\begin{align} r ^ 2 &= P_x ^ 2 - 2P_xC_x + C_x ^ 2 + P_y ^ 2 - 2P_yC_y + C_y ^ 2 \\ r ^ 2 &= (t(B_x - A_x) + A_x) ^ 2 - 2(t(B_x - A_x) + A_x)C_x + C_x ^ 2 \\ &+ (t(B_y - A_y) + A_y) ^ 2 - 2(t(B_y - A_y) + A_y)C_y + C_y ^ 2 \\ r ^ 2 &= t ^ 2 (B_x - A_x) ^ 2 + 2t(B_x - A_x)A_x + A_x ^ 2 - 2t(B_x - A_x)C_x - 2A_xC_x + C_x ^ 2 \\ &+ t ^ 2 (B_y - A_y) ^ 2 + 2t(B_y - A_y)A_y + A_y ^ 2 - 2t(B_y - A_y)C_y - 2A_yC_y + C_y ^ 2 \\ 0 &= t ^ 2 ((B_x - A_x) ^ 2 + (B_y - A_y) ^ 2) \\ &+ 2t((B_x - A_x)A_x - (B_x - A_x)C_x + (B_y - A_y)A_y - (B_y - A_y)C_y) \\ &+ A_x ^ 2 - 2A_xC_x + C_x ^ 2 + A_y ^ 2 - 2A_yC_y + C_y ^ 2 - r ^ 2 \\ 0 &= t ^ 2 ((B_x - A_x) ^ 2 + (B_y - A_y) ^ 2) \\ &+ 2t((B_x - A_x)(A_x - C_x) + (B_y - A_y)(A_y - C_y)) \\ &+ (A_x - C_x) ^ 2 + (A_y - C_y) ^ 2 - r ^ 2 \end{align}$

Решаем квадратное уравнение:

$\left\{\begin{align} a &= (B_x - A_x) ^ 2 + (B_y - A_y) ^ 2 \\ b &= 2((B_x - A_x)(A_x - C_x) + (B_y - A_y)(A_y - C_y)) \\ c &= (A_x - C_x) ^ 2 + (A_y - C_y) ^ 2 - r ^ 2 \\ \Delta &= b ^ 2 - 4ac \end{align}\right.$

$\Delta < 0$ : луч не пересекается с окружностью,
$\Delta = 0$ : луч пересекается с окружностью в одной точке (по касательной),
$\Delta > 0$ : луч пересекается с окружностью в двух точках.

Только в случае $\Delta = 0$ :

$\begin{align} t = \tfrac{-b}{2a} \end{align}$

Только в случае $t \geq 0$ :

$\left\{\begin{align} P_x &= t(B_x - A_x) + A_x \\ P_y &= t(B_y - A_y) + A_y \end{align}\right.$

Только в случае $\Delta > 0$ :

$\left\{\begin{align} t_1 &= \tfrac{-b -\sqrt{\Delta}}{2a} \\ t_2 &= \tfrac{-b +\sqrt{\Delta}}{2a} \\ \end{align}\right.$

Только в случае $t_i \geq 0$ :

$\left\{\begin{align} P_{i_x} &= t_i(B_x - A_x) + A_x \\ P_{i_y} &= t_i(B_y - A_y) + A_y \end{align}\right.$

Демо 11 — пересечение луча и окружности

Испускание лучей на окружности

Нам нужно найти две касательные к заданной окружности, проходящие через точку начала луча.

Пусть $inline$ — точки касательных, $inline$ — точка начала луча, $inline$ — центр окружности, а $inline$ — её радиус. Также мы будем перемещать все точки при помощи вектора переноса $\overrightarrow{v} = (-C_x, -C_y)$ : $X^\prime = X + \overrightarrow{v}$ так, чтобы центр окружности находился в $inline$ .

Из уравнения окружности:

$P_x ^ {\prime ^ 2} + P_y ^ {\prime ^ 2} = r ^ 2$

Из линии перпендикуляра к радиусу окружности:

$\left\{\begin{align} & P_x ^ {\prime ^ 2} + P_y ^ {\prime ^ 2} = r ^ 2 \\ & P_x ^ {\prime ^ 2} + P_y ^ {\prime ^ 2} = P_x ^ \prime A_x ^ \prime + P_y ^ \prime A_y ^ \prime \end{align}\right.$

Решаем систему уравнений:

$\left\{\begin{align} & P_x ^ {\prime ^ 2} + P_y ^ {\prime ^ 2} = r ^ 2 \\ & P_x ^ {\prime ^ 2} + P_y ^ {\prime ^ 2} = P_x ^ \prime A_x ^ \prime + P_y ^ \prime A_y ^ \prime \end{align}\right.$

$\begin{align} & r ^ 2 = P_x ^ \prime A_x ^ \prime + P_y ^ \prime A_y ^ \prime \\ & P_x ^ \prime = \tfrac{r ^ 2 - P_y ^ \prime A_y ^ \prime }{A_x ^ \prime} \text{, where } A_x ^ \prime \neq 0 \end{align}$

Подставляем $P_x ^ \prime$ в первое уравнение:

$\begin{align} & (\tfrac{r ^ 2 - P_y ^ \prime A_y ^ \prime }{A_x ^ \prime}) ^ 2 + P_y ^ {\prime ^ 2} = r ^ 2 \\ & \tfrac{r ^ 4 - 2 r ^ 2 P_y ^ \prime A_y ^ \prime + (P_y ^ \prime A_y ^ \prime) ^ 2}{A_x ^{\prime ^ 2}} + P_y ^ {\prime ^ 2} = r ^ 2 \\ & r ^ 4 - 2 r ^ 2 P_y ^ \prime A_y ^ \prime + (P_y ^ \prime A_y ^ \prime) ^ 2 + P_y ^ {\prime ^ 2} A_x ^{\prime ^ 2} = r ^ 2 A_x ^{\prime ^ 2} \\ & P_y ^ {\prime ^ 2} (A_x ^{\prime ^ 2} + A_y ^{\prime ^ 2}) - P_y ^ \prime 2r ^ 2 A_y ^ \prime + r ^ 4 - r ^ 2 A_x ^ {\prime ^ 2} = 0 \end{align}$

Решаем квадратное уравнение:

$\left\{\begin{align} a &= A_x ^{\prime ^ 2} + A_y ^{\prime ^ 2} \\ b &= - 2r ^ 2 A_y ^ \prime \\ c &= r ^ 4 - r ^ 2 A_x ^ {\prime ^ 2} \\ \Delta &= b ^ 2 - 4ac \end{align}\right.$

$\Delta < 0$ : точек касательных нет (точка начала луча находится внутри окружности),
$\Delta = 0$ : только одна точка касательной (точка начала луча),
$\Delta > 0$ : две точки касательных.

Только в случае $\Delta = 0$ :

$\left\{\begin{align} P_y ^ \prime &= \tfrac{-b}{2a} \\ P_x ^ \prime &= \tfrac{r ^ 2 - P_y ^ \prime A_y ^ \prime }{A_x ^ \prime} \end{align}\right.$

$\left\{\begin{align} P_x &= P_x ^ \prime + C_x \\ P_y &= P_y ^ \prime + C_y \end{align}\right.$

Только в случае $\Delta > 0$ :

$\left\{\begin{align} P_{1_y} ^ \prime &= \tfrac{-b -\sqrt{\Delta}}{2a} \\ P_{2_y} ^ \prime &= \tfrac{-b +\sqrt{\Delta}}{2a} \\ P_{i_x} ^ \prime &= \tfrac{r ^ 2 - P_{i_y} ^ \prime A_y ^ \prime }{A_x ^ \prime} \end{align}\right.$

$\left\{\begin{align} P_{i_x} &= P_{i_x} ^ \prime + C_x \\ P_{i_y} &= P_{i_y} ^ \prime + C_y \end{align}\right.$

Но есть ещё одна проблема — это не сработает, если $A_x ^ \prime = 0$ . Присмотримся к следующему уравнению: $r ^ 2 = P_x ^ \prime A_x ^ \prime + P_y ^ \prime A_y ^ \prime$ . Если $A_x ^ \prime = 0$ , уравнение принимает следующий вид: $r ^ 2 = P_y ^ \prime A_y ^ \prime$ — больше мы не можем подставить $P_x ^ \prime$ . Вот как решить эту систему уравнений, если такое случится:

Решаем систему уравнений:

$\left\{\begin{align} & P_x ^ {\prime ^ 2} + P_y ^ {\prime ^ 2} = r ^ 2 \\ & P_x ^ {\prime ^ 2} + P_y ^ {\prime ^ 2} = P_x ^ \prime A_x ^ \prime + P_y ^ \prime A_y ^ \prime \\ & A_x ^ \prime = 0 \end{align}\right.$

$\begin{align} & r ^ 2 = P_y ^ \prime A_y ^ \prime \\ & P_y ^ \prime = \tfrac{r ^ 2}{A_y ^ \prime} \text{, where } A_y ^ \prime \neq 0 \end{align}$

Подставим $P_y ^ \prime$ в первое уравнение:

$\begin{align} & P_x ^ {\prime ^ 2} + (\tfrac{r ^ 2}{A_y ^ \prime}) ^ 2 = r ^ 2 \\ & P_x ^ {\prime ^ 2} + \tfrac{r ^ 4}{A_y ^ {\prime ^ 2}} = r ^ 2 \\ & P_x ^ {\prime ^ 2} A_y ^ {\prime ^ 2} + r ^ 4 = r ^ 2 A_y ^ {\prime ^ 2} \\ & P_x ^ {\prime ^ 2} A_y ^ {\prime ^ 2} + r ^ 4 - r ^ 2 A_y ^ {\prime ^ 2} = 0 \end{align}$

Решим квадратное уравнение:

$\left\{\begin{align} a &= A_y ^ {\prime ^ 2} \\ b &= 0 \\ c &= r ^ 4 - r ^ 2 A_y ^ {\prime ^ 2} \\ \Delta &= b ^ 2 - 4ac \end{align}\right.$

$\Delta < 0$ : точки касательной не существует (точка начала луча находится внутри окружности),
$\Delta = 0$ : только одна точка касательной (точка начала луча),
$\Delta > 0$ : две точки касательных.

Только в случае $\Delta = 0$ :

$\left\{\begin{align} P_x ^ \prime &= \tfrac{-b}{2a} \\ P_y ^ \prime &= \tfrac{r ^ 2}{A_y ^ \prime} \end{align}\right.$

$\left\{\begin{align} P_x &= P_x ^ \prime + C_x \\ P_y &= P_y ^ \prime + C_y \end{align}\right.$

Только в случае $\Delta > 0$ :

$\left\{\begin{align} P_{1_x} ^ \prime &= \tfrac{-b -\sqrt{\Delta}}{2a} \\ P_{2_x} ^ \prime &= \tfrac{-b +\sqrt{\Delta}}{2a} \\ P_{i_y} ^ \prime &= \tfrac{r ^ 2}{A_y ^ \prime} \end{align}\right.$

$\left\{\begin{align} P_{i_x} &= P_{i_x} ^ \prime + C_x \\ P_{i_y} &= P_{i_y} ^ \prime + C_y \end{align}\right.$

Заметьте, что тоже самое мы можем сделать при $A_y ^ \prime = 0$ , однако это необязательно. Если $A_x ^ \prime = A_y ^ \prime = 0$ , то решений нет.

Демо 12 — испускание лучей на окружности

Способы оптимизации

В этом разделе мы поговорим об использовании пространственных хэш-карт и модифицированного алгоритма рисования линий Брезенхэма. Я не буду вдаваться в подробности реализации, потому что они широко доступны в Интернете. Однако я напишу несколько демо, чтобы вы могли их тестировать и придумывать новые идеи их применения.

Пространственные хэш-карты

Пока мы отрисовываем все многоугольники и вычисляем все точки пересечения, но это практически бесполезно. В большинстве случаев игровая область гораздо больше окна обзора. При помощи пространственных хэш-карт мы можем быстро определять, какие многоугольники видны игроку и выполнять адекватные вычисления.

По сути, мы хотим разделить игровую область на меньшие ячейки (заданного размера). Каждая ячейка состоит из списка, содержащего фигуры (чаще всего это отрезки прямых). Если одна фигура растянулась на несколько ячеек, то она будет включена во все эти ячейки.

Из названия этой методики понятно, что в ней используются хэш-карты (т.е. ячейки будут иметь названия вида X+":"+Y), но в нашем случае желательней будет простой 2D-массив.

Вот простое демо, показывающее, как это может работать:

Демо 13 — пространственные хэш-карты

Как говорилось выше, мы можем применять их для окон обзора, а также для окружностей видимости и фонариков.

Линия сверхпокрытия на основе алгоритма Брезенхэма

При помощи пространственных хэш-карт и модифицированного алгоритма отрисовки линий Брезенхэма мы можем эффективным образом обходить сетку, выполняя минимальное количество проверок. Алгоритм должен завершать выполнение после обнаружения первой ячейки с точкой пересечения.

Подробнее об алгоритме отрисовки линий Брезенхэма можно прочитать здесь, а об его модифицированной версии — здесь.

Демо 14 — Линия сверхпокрытия на основе алгоритма Брезенхэма

Всё имеет свой конец

Простите, к сожалению, я говорю об этой статье, а не о лучах.

Думаю, мы раскрыли всё необходимое для того, чтобы вы могли приступить к работе. Если я найду что-то, требующее дальнейшего объяснения, то постараюсь дополнить статью. Кроме того, я создал небольшую шпаргалку для напоминания о некоторых темах и выведенных формулах.

Если вам понравилась статья, то поставьте звёздочку и подпишитесь на этот репозиторий на GitHub.

Теги:

Хабы:

Если эта публикация вас вдохновила и вы хотите поддержать автора — не стесняйтесь нажать на кнопку

Рейкастинг в игровых 2D-движках

Введение

Что такое рейкастинг?

Где может использоваться рейкастинг?

Создание 3D-перспективы на 2D-карте

Задача точки в многоугольнике

Видимость объектов и испускание света

Видимость объектов и испускание света в 2D-играх

Точка пересечения отрезка и луча

Вывод параметрического уравнения прямой

Вычисление точки пересечения

Поиск ближайшей точки пересечения

Испускание лучей

Испускание лучей по углу смещения

Испускание лучей в вершины

Освещение видимой области

Сортировка точек пересечения

Испускание лучей с небольшим смещением

Круг видимости и фонарик

А как насчёт окружностей?

Точка пересечения окружности и луча

Испускание лучей на окружности

Способы оптимизации

Пространственные хэш-карты

Линия сверхпокрытия на основе алгоритма Брезенхэма

Всё имеет свой конец

Публикации

Истории

Работа

Ближайшие события