Данная статья в большей мере является уточнением моей предыдущей статьи по оптимизации перебора на шахматной доске с ферзями.
https://habr.com/ru/post/679200/
Оптимизация перебора в данной задаче, это не только лишь хардкорное скоростное решение на базе 64-битной арифметики и SIMD-стиля. Это внесение в алгоритм решений, позволяющее сократить само количество шагов перебора. Пока я представляю начальный позиционный анализ.
Уточнением к моей предыдущей статье, является то что я добавил позиционный анализ не только к столбцам, но и к строкам. Пришлось довольно долго помучится для наиболее эффектной реализации. Задача крылась в решении, как быстро просуммировать атаки в строке шахматной доски, если я базовое движение совершаю по столбцам. Перепробовав несколько вариантов с битовыми играми, я остановился на том чтобы во время маркировки атак, вести альтернативную шахматную доску повернутую так, что X и Y просто меняются местами (инверсия осей). Для этого потребовалось ввести только три дополнительные переменные.
Некоторые коллеги читавшие мою статью, видимо не уловили смысл происходящего и пытаются утверждать, что всё равно совершается полный перебор позиций на доске. Но это совершенно не так.
Оптимизирующий алгоритм выглядит сейчас так:
Перед установкой нового ферзя:
Проверить, что на доске стоит полный комплект ферзей. Если да, то рапортовать об успехе. Снять последнего установленного ферзя, шаг назад.
Определить есть ли такой столбец на ВСЕЙ доске, в котором нет ферзя, но все клетки этого столбца являются атакованными. Если такой столбец имеется, то прервать перебор, шаг назад
Определить есть ли такая строка на ВСЕЙ доске, в которой нет ферзя, но все клетки этой стоки являются атакованными. Если такая строка имеется, то прервать перебор, шаг назад.
Определить есть ли такой столбец на ВСЕЙ доске, в котором нет ферзя, но можно поставить только одного ферзя. Если такой столбец имеется, то поставить туда ферзя, перейти к пункту №1.
Определить есть ли такая строка на ВСЕЙ доске, в которой нет ферзя, но можно поставить только одного ферзя. Если такая строка имеется, то поставить туда ферзя, перейти к пункту №1.
Берем свободный столбец ближе к началу, определяем свободные места в нем, начинаем перебором ставить туда ферзей. Поставив очередного ферзя идем к пункту №1.
Для понимания практичности этого анализа приведу иллюстрации:

По классике базовое движение по столбцам A-H, выставляем перебором ферзей по строкам №1-8. Имеем трёх установленных ферзей A1,B3,C5. "Как бы" собираемся прогуляться перебором по столбцу D в котором осталось три свободные клетки: D2,D7 и D8.
Но тут "Как бы" выключается и включается мой механизм оптимизации перебора...
Когда приступаем к установке 4-го ферзя, обнаруживаем, что на доске образовался такой столбец, что в него можно поставить только одного ферзя. Это позиция F4. Эта позиция отстоит вперёд на два столбца, то есть не является следующей-очередной. Установка туда ферзя уже не засчитывается, как перебор, так как "очередной" столбец D имеет три свободные клетки. Внеочередную установку ферзя в F4 я называю - реверсом.

Установкой ферзя F4 - замечательным образом мы заодно выбьем клетку D2 с которой бы начался классический перебор на 4-го ферзя. Но тут уже видно, что следующим кандидатом на ферзя будет клетка H7, поскольку она осталась единственной в колонке H.

Проставив H7 мы атакуем клетку G6. И в следствии атаки на G6 возникает ситуация, что строка №6 не имеет ферзя, но все клетки строки №6 являются атакованными. В данном случае после установки пятого ферзя, выясняется, что данная комбинация не имеет продолжения, два ферзя F4 и H7 снимаются с доски, ферзь с C5 перемещается на C6.
На доске после 5-го ферзя остались "не перебранными" клетки: D8, E2, E8, G2
Как бы сказал шахматист, - поставив ферзей на A1+B3+C5 - мы получаем образно выражаясь - "мат в два хода".
Классические алгоритмы по расстановке ферзей обычно движутся строго линейно, и циклично осуществляют маркировки атак "вперед". В моём алгоритме все маркировки атак заготовлены заранее и предусматривают маркировку атак "назад".
Хардкорные битово-арифметические операции мне позволяют достаточно быстро производить анализ текущих атак. Новый листинг алгоритма прилагается.
using System; //using System.Numerics.BitOperations; using System.Runtime.InteropServices; namespace Queen_8x8 { delegate void Solution(int[] queens); class Program { static Queen_8x8 task = new Queen_8x8(); static void Main(string[] args) { print("Hello Queens!"); print(":"); task.init(print_solution); //task.init(null); task.run(); print(":"); print("solution_count = " + task.solution_count); print("solve_count = " + task.solve_count); print("reverse_count = " + task.reverse_count); print("break_count = " + task.break_count); } static void print(String s) { Console.WriteLine(s); } static void print_solution(int[] queens) { String s = ""; s += "[ "; for (int i = 0; i < queens.Length; i++) { s += Char.ConvertFromUtf32(i + 65) + (queens[i] + 1).ToString(); if (i < (queens.Length - 1)) s += ", "; } s += " ]"; print(s); } } class Queen_8x8 { protected Solution solution = null; public const int total_queens_count = 8; public const int diag_count = total_queens_count * 2 - 1; //public ulong markers = 0xFFFF_FFFF_FFFF_FFFF; public int[] queens = new int[total_queens_count]; int current_queens_count = 0; ulong[] diag_LR = new ulong[diag_count]; ulong[] diag_RL = new ulong[diag_count]; public ulong attacks_VT = 0; // атака по вертикали public ulong attacks_VZ = 0; public ulong attacks_HZ = 0; // атака по горизонтали public ulong attacks_HT = 0; public ulong attacks_LR = 0; // атака по диагонали BL-TR [\] public ulong attacks_RL = 0; // атака по диагонали BR-TL [/] // Инверсные атаки по диагоналям. X и Y меняются местами // Введедены для последующего быстрого суммирования атак по строкам public ulong attacks_LRZ = 0; public ulong attacks_RLZ = 0; // Statisticks public int solution_count = 0; public int solve_count = 0; public int reverse_count = 0; public int break_count = 0; static void print(String s) { Console.WriteLine(s); } private int get_LR(int x, int y) { return x + y; } private int get_RL(int x, int y) { return (total_queens_count - 1 - x) + y; } private void reset() { solution_count = 0; solve_count = 0; reverse_count = 0; break_count = 0; current_queens_count = 0; attacks_VT = 0; attacks_HT = 0; attacks_HZ = 0; attacks_VZ = 0; attacks_LR = 0; attacks_RL = 0; attacks_LRZ = 0; attacks_RLZ = 0; for (int i = 0; i < queens.Length; i++) { queens[i] = -1; } current_queens_count = 0; } public void run() { reset(); solve(); } public void init(Solution solution) { this.solution = solution; for (int i = 0; i < diag_count; i++) { diag_LR[i] = 0; diag_RL[i] = 0; } for (int x = 0; x < total_queens_count; x++) { for (int y = 0; y < total_queens_count; y++) { ulong mask = 1UL << ((x << 3) + y); diag_LR[get_LR(x, y)] |= mask; diag_RL[get_RL(x, y)] |= mask; } } } protected void step(int qx, int qy) { ulong a_VT = 0xFFUL << (qx << 3); ulong a_HT = 0xFFUL << (qy << 3); ulong a_VZ = 0x0101_0101_0101_0101UL << qx; ulong a_HZ = 0x0101_0101_0101_0101UL << qy; ulong a_LR = diag_LR[get_LR(qx, qy)]; ulong a_RL = diag_RL[get_RL(qx, qy)]; ulong a_LRZ = diag_LR[get_LR(qy, qx)]; ulong a_RLZ = diag_RL[get_RL(qy, qx)]; // Set Queeen ++current_queens_count; queens[qx] = qy; attacks_VT |= a_VT; attacks_HT |= a_HT; attacks_HZ |= a_HZ; attacks_VZ |= a_VZ; attacks_LR |= a_LR; attacks_RL |= a_RL; attacks_LRZ |= a_LRZ; attacks_RLZ |= a_RLZ; // Recurse solve(); // Remove Queeen attacks_VT &= ~a_VT; attacks_HT &= ~a_HT; attacks_HZ &= ~a_HZ; attacks_VZ &= ~a_VZ; attacks_LR &= ~a_LR; attacks_RL &= ~a_RL; attacks_LRZ &= ~a_LRZ; attacks_RLZ &= ~a_RLZ; queens[qx] = -1; --current_queens_count; } protected void solve() { if (current_queens_count == total_queens_count) { ++solution_count; solution?.Invoke(queens); return; } // Проверка по столбцам ulong attacks_v = attacks_HZ | attacks_VT | attacks_LR | attacks_RL; // Получаем в каждом байте 64-разрядного числа - // сумму занятых мест по столбцам // Каждый байт обозначает столбец таблицы и содержит число // атак в интервале от 0 до 8 ulong sum_vec_8_columns = BitOp.popcnt64_bv(attacks_v); // Проверка, что остались незаполненные столбцы // Определяем что в каком либо столбце присуствует число 8 // Если в каком-либо столбце присутствует число 8, // то общее значение теста станет ненулевым ulong test = sum_vec_8_columns & 0x0808_0808_0808_0808UL; // Маскируем байты для обнаружения числа 8 test &= ~attacks_VT; // Отбрасывем столбцы (columns), где уже установлены ферзи if (test != 0) { ++break_count; return; // Нашёлся столбец, куда невозможно установить ферзя } // Проверка по строкам ulong attacks_h = attacks_HT | attacks_VZ | attacks_LRZ | attacks_RLZ; // Получаем в каждом байте 64-разрядного числа - // сумму занятых мест по строкам // Каждый байт обозначает строку таблицы и содержит число // атак в интервале от 0 до 8 ulong sum_vec_8_rows = BitOp.popcnt64_bv(attacks_h); test = sum_vec_8_rows & 0x0808_0808_0808_0808UL; // Маскируем байты для обнаружения числа 8 test &= ~attacks_HT; // Отбрасывем строки (rows), где уже установлены ферзи if (test != 0) { ++break_count; return; // Нашлась строка, куда невозможно установить ферзя } int qx, qy; ulong column, row; // Проверка, на то что есть столбцы, только с одим возможным ходом // Поскольку мы отбросили вариант, что в столбцах присутствует число 8 // прибавляем к каждому столбцу единицу и опять проверяем все столбцы // на наличие числа 8 // Если изначально в каком-либо столбце присутствовало число 7, // то общее значение теста станет ненулевым test = sum_vec_8_columns + 0x0101_0101_0101_0101UL; test &= 0x0808_0808_0808_0808UL & ~attacks_VT; if (test != 0) { ++reverse_count; qx = BitOp.bsf64((test >> 3)) >> 3; column = (~attacks_v >> (qx << 3)) & 0xFFUL; qy = BitOp.bsf64(column); step(qx, qy); return; } // Аналогичным образом, проверяем, что есть такая строка в которую можно // поставить только одного ферзя test = sum_vec_8_rows + 0x0101_0101_0101_0101UL; test &= 0x0808_0808_0808_0808UL & ~attacks_HT; if (test != 0) { ++reverse_count; qy = BitOp.bsf64((test >> 3)) >> 3; row = (~attacks_h >> (qy << 3)) & 0xFFUL; qx = BitOp.bsf64(row); step(qx, qy); return; } // Делаем перебор по столбцу test = sum_vec_8_columns + 0x0202_0202_0202_0202UL; test &= 0x0808_0808_0808_0808UL & ~attacks_VT; if (test != 0) { qx = BitOp.bsf64((test >> 3)) >> 3; } else { qx = BitOp.bsf64(~attacks_VT) >> 3; } //-- column = (~attacks_v >> (qx << 3)) & 0xFFUL; while (column != 0) { ++solve_count; qy = BitOp.bsf64(column); column &= column - 1; // BLSR BMI1!!! column &= ~(1UL << qy); // Сбросить самый младший единичный бит step(qx, qy); } return; } } class BitOp { // Просумировать все биты в байтах 64-разрядного числа public static ulong popcnt64_bv(ulong value) { ulong result = value; result = result - ((result >> 1) & 0x5555_5555_5555_5555UL); // Результат сумм по 2-а бита result = (result & 0x3333_3333_3333_3333UL) + ((result >> 2) & 0x3333_3333_3333_3333UL); // Результат сумм по 4-е бита result = (result + (result >> 4)) & 0x0F0F_0F0F_0F0F_0F0F; // Результат сумм по 8-ь бит return result; } public static byte add64_bv(ulong value) { ulong result = value; result += result >> 8; // Результат сумм по 16-ь бит result += result >> 16; // Результат сумм по 32-ь бит result += result >> 32; // Результат return (byte)(result); } /* * Подсчитать кол-во битов установленных в 1 в 64-разрядном числе * Полностью эквивалентна машинной инструкции Intel x86/x64 - POPCNT */ public static byte popcnt64(ulong value) { ulong result = value; result = result - ((result >> 1) & 0x5555_5555_5555_5555UL); // Результат сумм по 2-а бита result = (result & 0x3333_3333_3333_3333UL) + ((result >> 2) & 0x3333_3333_3333_3333UL); // Результат сумм по 4-е бита result = (result + (result >> 4)) & 0x0F0F_0F0F_0F0F_0F0F; // Результат сумм по 8-ь бит result += result >> 8; // Результат сумм по 16-ь бит result += result >> 16; // Результат сумм по 32-ь бит result += result >> 32; // Результат return (byte)(result); } public static byte popcnt8(byte value) { ulong result = value; result = result - ((result >> 1) & 0x55); // Результат сумм по 2-а бита result = (result & 0x33) + ((result >> 2) & 0x33); // Результат сумм по 4-е бита result = (result + (result >> 4)) & 0x0F; // Результат сумм по 8-ь бит return (byte)(result); } public static int bsf64(ulong value) { if (value == 0) return -1; int bitpos = 0; ulong mask = 0xFFFF_FFFF_FFFF_FFFFUL; int step = 64; while ((step >>= 1) > 0) // 6-итерационный проход { if ((value & (mask >>= step)) == 0) { value >>= step; bitpos |= step; } } return bitpos; } } }
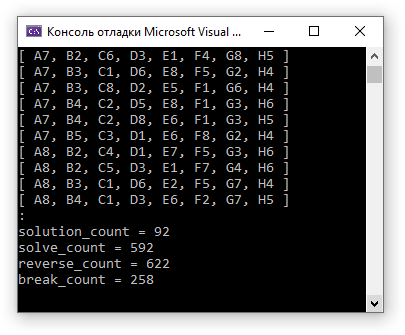
2056 ./ 592 = 3,5 - Сокращение вариантов перебора.
2056 - как говорилось в предыдущей статье, количество. шагов перебора без моего позиционного анализа.
Если двигать первого ферзя только по клеткам A1-A4, кол-во переборов уменьшается вдвое
592 / 2 = 296
Я предварительно для статьи пытаюсь убрать из алгоритма всё обрамление и мои исследования, чтобы осталась только чистая логика оптимизации.
P.S. Продолжение возможно последует...
