Vector Space Model (VSM) – это математическая модель представления текстов, в которой каждому документу сопоставлен вектор, выражающий его смысл. Такое представление позволяет легко сравнивать слова, искать похожие, проводить классификацию, кластеризацию и многое другое. Но обо всём по порядку.
Чтобы не произошло путаницы, сразу же сделаю пояснение. Существует два основных подхода к семантическому поиску, да и вообще к сравнению документов по смыслу. Первый подход основан на ручном наделении объектов некоторыми атрибутами и обработке именно атрибутов, а не самих объектов. Сюда можно отнести тегирование, ручную каталогизацию, онтологии и, конечно же, концепцию Web 3.0. Суть всегда одна и та же – большое количество людей создаёт базу знаний, то есть набор триплетов <субъект, предикат, объект>, плюс, в некоторых случаях, правила вывода. Иногда, правда, процесс извлечения знаний пытаются автоматизировать. Так, например, существуют системы, строящие триплеты по предложениям на естественных языках. Грубо говоря, из предложения «12 апреля 1953 года состоялось бракосочетание сенатора Кеннеди и Жаклин Бувье» такая система способна вывести логическую связку <Джон_Кеннеди, женат_на, Жаклин_Бувье>. Однако создание и развитие таких систем всё ещё требует большого количества ручной работы, причём работы не простых пользователей или верстальщиков, а профессиональных программистов и лингвистов.
Второй подход, о котором и пойдёт речь, основан на противоположной идее: вместо сложных логических правил используется простая математическая модель, вместо тысяч часов ручной работы – статистический анализ уже существующих текстов. Начало этот подход берёт в работах над методом LSA (Latent Semantic Analysis, неявный семантический анализ). Позже метод претерпел множество модификаций и получил довольно широкую известность. Достаточно сказать, что сегодня Google и ряд других крупных поисковиков используют один из параметров данного метода (а именно так называемый индекс tf*idf) при ранжировании результатов.
Итак, в чём же суть подхода, и какие существуют методы для его реализации?
Основная идея проста до безобразия: чем чаще два слова встречаются в одних и тех же контекстах (документах), тем ближе они по смыслу. Действительно, можно ожидать, что слова «программирование» и «алгоритм» будут встречаться в одних и тех же документах гораздо чаще, чем, например, «программирование» и «собаководство». Для LSA частота встречаемости в конкретном документе зачастую представляется как раз в виде индекса tf*idf, что расшифровывается как «term frequency * inverse document frequency». Term frequency – частота термина – рассчитывается как количество вхождений конкретного термина в конкретный документ, делённое на общее количество слов в этом документе:
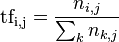
Document frequency – частота документа – это количество документов, в которых данный термин встречается, делённое на общее количество документов. Inverse document frequency, соответственно, это величина, обратная document frequency, то есть idf = 1/df. Обычно, чтобы как-то смягчить эффект действия idf на общий результат, вместо самого значения берётся его логарифм:
В общем-то, индекс tf*idf уже можно использовать для ранжирования результатов поиска – чем выше индекс, тем больше релевантность данного термина в данном документе. Тем не менее, для более сложных задач, таких как сравнение двух документов, этого всё ещё не достаточно.
Все индексы tf*idf для всех терминов и всех документов можно занести в единую таблицу:
Заголовки строк матрица – термины, заголовки столбцов – документы. Элементы самой матриц будем называть «веса». Каждая строка представляет собой распределение индексов терминов по документам, каждый столбец – распределение документов по терминам, то есть получается взаимное выражение терминов через документы, в которых они встречаются, и документов через термины, из которых они состоят, поэтому все законы, применимые для сравнения терминов будут также работать и для сравнения целых документов. Для простоты и краткости изложения далее при описании данного метода я буду говорить только про распределение терминов.
Авторы LSA предположили, что два термина будут тем более похожи по смыслу, чем ближе будут соответствующие строки нашей матрицы (вспомните пример про программирование-алгоритм-собаководство). Меру схожести двух строк можно измерять различными способами, например, с помощью поэлементной разницы.
Остаётся одна проблема – размер матрицы. Если мы работаем с более или менее крупным корпусом текстов, то количество терминов будет измеряться в тысячах и десятках тысяч, а про документы и говорить не стоит. Даже просто держать такую матрицу в памяти крайне накладно, а поиск похожих терминов – это жесточайший удар по производительности системы. Чтобы решить эту проблему, было решено редуцировать матрицу, то есть уменьшать её размер до приемлемого.
Естественно, при уменьшении ранга матрицы желательно сохранить наиболее «важные» её элементы, то есть те, которые образуют базис соответствующего пространства. Самым эффективным методом для решения этой задачи считается сингулярное разложение (Singular Value Decomposition, SVD). Его описание можно найти здесь.
К сожалению, при всей своей математической эффективности SVD не решает проблемы с памятью, поскольку перед применением алгоритма редуцирования всё ещё требуется загрузка полной начальной матрицы. Кроме того, каждый раз при добавлении документа всю процедуру необходимо повторять.
Сделаем шаг назад и посмотрим на всю картину целиком. У нас есть предположение, что слова, встречающиеся в одних и тех же контекстах (документах), а также контексты (документы), содержащие одни и те же слова, являются близкими по смыслу. Информацию о совместной встречаемости можно организовать в виде матрицы или, что то же самое, в виде набора векторов в некотором многомерном пространстве. Например, если взять матрицу, которую мы строили для LSA, то её строки будут представлять собой T векторов в D-мерном пространстве, где T – количество терминов, а D, соответственно, — количество документов. Это и составляет суть моделей векторного пространства1. Чтобы как-то различать документы, необходим некий способ уникально представить каждый из них в виде вектора. Простейший способ осуществить это – сделать их все ортогональными, то есть построить на их основе единичную матрицу:
Тогда позиция единицы в векторе будет однозначно идентифицировать документ.
Здесь мы возвращаемся к проблеме потребления памяти и уменьшению ранга матрицы (количества измерений). Нам всё ещё необходимо уникально представить каждый документ, однако использовать для этого не D измерений, а гораздо меньше.
К счастью оказалось, что в многомерном пространстве гораздо больше почти ортогональных направлений, чем действительно ортогональных. Это значит, что мы можем аппроксимировать нашу единичную матрицу просто заменив единственные ненулевые элементы в векторах наших документов набором из нескольких ненулевых элементов на случайно выбранных позициях. То есть вместо представленной выше матрицы мы получим что-то вроде:
А это именно то, что нам и нужно. Важной особенностью здесь является тот факт, что при добавлении новых документов нет необходимости увеличивать размерность векторов всех документов, то есть длина векторов остаётся фиксированной.
О’кей, мы получили способ уникально представлять документы в векторном пространстве. Что дальше? А дальше нам необходимо выразить термины через документы, в которых они встречаются.
В LSA мы использовали вектора (строки матрицы), составленные из значений некоторой функции частоты встречаемости (в примере выше – это tf*idf). Каждый из этих элементов можно разложить на элементы, представив в виде суммы ортогональных векторов, т.е., например, вектор:
можно представить в виде:
Каждое из слагаемых – это вектор, уникально характеризующий документ, умноженный на значение функции частоты текущего термина. То есть, с математической точки зрения термин можно выразить через содержащие его документы просто сложив вектора этих самых документов (с учётом частоты, разумеется). И в данном случае не имеет значения, являются ли вектора документов действительно ортогональным (как в LSA) или почти ортогональными.
Таким образом, вектор термина будет равен:
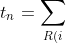}^{ }f_{ni}\cdot d_i "t_{n}=\sum_{R(i)}^{ }f_{ni}\cdot d_i")
где "R(i)")
— область определения для векторов документов, т. е. просто номера используемых документов;
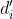— начальный вектор i-ого документа;
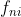— частота n-ого термина в i-ом документе.
Частота здесь может рассчитываться просто как количество вхождений данного термина в документ. В данном случае нормализация частоты не требуется (об этом ниже), поэтому храниться и обрабатываться будут целые числа.
Обратите внимание, что размер векторов t уже не зависит от количества документов в корпусе – он всегда фиксирован и равен тому значению, которое мы задали для начальных векторов документа.
Ну и последний момент. Слова сравнивать по смыслу, конечно, интересно, но непрактично. Сравнивать нам нужно тексты, т. е. документы. И тут закономерный вопрос – как выразить документы через содержащиеся в них слова? Ответ: точно так же, как и слова через документы: сложив вектора соответствующих объектов:
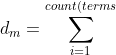}t_i "d_m=\sum_{i=1}^{count(terms)}t_i")
где "count(terms)")
— количество терминов (не обязательно уникальных) в документе;
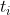— i-тый термин в тексте;
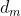— вектор m-ного документ.
Ещё раз: мы случайным образом генерируем начальные вектора для документов (d’), затем на их основе рассчитываем вектора всех терминов (t), и уже из них получаем окончательные вектора документов (d).
Описанный выше метод носит название Random Indexing (примерный перевод – «индексирование случайными числами»)2.
Так что же дают векторные представления документов?
Во-первых, их можно сравнивать. Два вектора будут тем ближе, чем меньше угол между ними. Для оценки угла достаточно взять любую монотонно-возрастающую функцию, например, косинус:
=\frac{\overrightarrow{a} \cdot \overrightarrow{b}}{\left | \overrightarrow{a} \right |\cdot \left | \overrightarrow{b} \right |}=\frac{\sum_{R(i)}^{ }{a_ib_i}}{\sqrt{\sum_{R(i)}^{ }{a_i^2}}\cdot\sqrt{\sum_{R(i)}^{ }{b_i^2}}} "cos(\overrightarrow{a}, \overrightarrow{b})=\frac{\overrightarrow{a} \cdot \overrightarrow{b}}{\left | \overrightarrow{a} \right |\cdot \left | \overrightarrow{b} \right |}=\frac{\sum_{R(i)}^{ }{a_ib_i}}{\sqrt{\sum_{R(i)}^{ }{a_i^2}}\cdot\sqrt{\sum_{R(i)}^{ }{b_i^2}}}")
Произведение векторов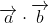
показывает, насколько похожи два документа, а произведение их длин выступает в роли фактора нормализации. Если произведение не нормализовать, то, например, два документа по 100 слов со всего 5-ю общими элементами в векторах дадут более высокий результат, чем два документа по 10 слов с 3-мя общими элементами. Иногда это тоже бывает полезно, но в большинстве случаев предпочитают брать относительное значение в пределах [0, 1] (в этом случае «0» означает отсутствие общих направлений у векторов документов, а «1», по сути, — полное их совпадение).
Во-вторых, что не менее важно, над ними можно проводить все те же операции, что и над обычными векторами – сложение, вычитание и даже умножение на скаляр. Нетрудно догадаться, как будут интерпретироваться эти операции: сложение – это просто объединение двух текстов, умножение на скаляр – повторение одного и того же текста несколько раз и т. д.
Как только в систему введена мера близости двух объектов, можно начинать использовать алгоритмы классификации и кластеризации. Кластеризация, то есть классификация по заранее неизвестным классам, — тема насколько интересная, настолько и большая, поэтому и требующая отдельной статьи. Здесь же остановимся только на классификации.
Классификация – это отнесение объекта (в нашем случае текста) к одному из предопределённых классов. Чтобы не возникло путаницы с терминологией, будем называть эти классы корзинами. Каждая корзина представляет собой просто вектор. Это может быть вектор конкретного термина (например, «математика»), канонического документа (конспект лекций по математике) или набора документов. Степень близости текста и корзины определяется всё тем же косинусом (или любой другой функцией расстояния) между векторами этих объектов.
Есть два основных типа классификации:
К первому типу относятся, например, фильтры спама: письмо так или иначе должно быть классифицировано в одну из двух папок – Inbox или Spam. Классификация проводится просто сравнением косинусов для всех доступных корзин – где значение больше, туда и классифицируем.
Чуть сложнее обстоит дело с классификацией в несколько корзин. Наиболее полно модель классификации на множество классов описывает теория нечётких множеств.
Классическая теория множеств имеет дело с бинарным признаком вхождения – некий объект либо входит, либо не входит во множество. Нечёткие же множества позволяют градуировать степень вхождения (принадлежности). Например, можно сказать: «данный объект принадлежит данному множеству со степенью 0.7».
Для оценки степени принадлежности используется, как нетрудно догадаться, функция принадлежности. И вот тут мы видим полное соответствие задаче классификации – корзины можно рассматривать как множества, классифицируемые тексты – как объекты, а в качестве функции принадлежности используется функция близости векторов.
Если необходимо бинарно определить, принадлежит ли текст некоторой корзине, используется пороговое значение. Значение это может быть как постоянным, так и плавающим.
В качестве примера модели классификации с плавающим значением рассмотрим улучшение обычной классификации с использованием деревьев. Если некую область знаний можно описать как иерархию понятий, то эту область возможно представить в виде дерева с большим количеством ветвей. Например, понятие «наука» может является корнем и иметь детей «физика», «химия», «математика», понятие «математика», в свою очередь, может является родителем для «теория чисел», «теория множеств», «планиметрия» и т.д. Построение такого дерева начинается снизу – листья формируются из реальных текстов по указанной теме, а узлы представляют собой просто сумму векторов всех своих детей. Так, например, «математика» — это «теория множеств» + «теория чисел» + «планиметрия», а «наука» — это сумма всех научных направлений.
Классификация производится рекурсивно: вначале проверяется, может ли данный текст быть отнесён к текущему корню, и если да, то ссылка на эту корзину сохраняется (аккумулируется), а процедура повторяется для всех детей. Выигрыш здесь не только в возможности обобщения понятий, но и в производительности – если линейная классификация занимала O(n) времени, то иерархическая – всего лишь около O(log n).
Проблема здесь состоит в том, что длины векторов корня и листьев сильно отличаются, и при фиксированном пороге вхождения текст может просто «не дойти» до листьев, остановившись ещё на корне. Чтобы этого не произошло, пороговое значение должно быть плавающим и представлять собой функцию от длины вектора корзины. В зависимости от задачи это может быть константа, делённая либо на длину вектора, либо на какое то «смягчённое» значение, например, корень квадратный из этой самой длины.
Когда я только начинал заниматься этой темой, был сильно удивлён, что не смог найти приемлемой библиотеки для реализации VSM на целевой платформе (на тот момент это была JVM). Всё, что мне удалось отыскать, – это либо готовые
реализации сравнения документов через tf*idf, либо 
консольные имплементации, абсолютно непригодные для модификаций. К счастью, самостоятельная реализация оказалась довольно простой задачей. Данная статья уже содержит всю необходимую для этого информацию, однако я сделаю ещё несколько небольших замечаний.
Во-первых, алгоритм активно использует информацию о частоте слов, а также требует синтаксического и морфологического разбора входных текстов. То есть использует всё то же, что и поисковые движки. Поэтому в качестве базы для реализации модели лучше всего использовать именно их. Одной из лучших свободных реализаций поискового движка является Lucene. Сам по себе Lucene написан на Java, однако существует огромное количество портов на другие языки и платформы, в том числе .NET, С++, Delphi, Python, Ruby и многие другие.
Во-вторых, представление векторов, использованное в данной статье для Random Indexing, является не совсем верным и совсем неэффективным. В примере вектора имели бинарные элементы – либо 0 (большинство), либо 1. На самом деле более эффективно использовать тринарные элементы: -1, 0 или 1. Знак ненулевых элементов выбирается, так же как и позиция, случайно.
Поскольку вектора сильно разряжённые (я использовал 2-20 ненулевых значений для векторов длиной 5000-1000 элементов), то их намного эффективней представлять не в виде единого вектор, хранящего и единицы, и нули, а список пар. То есть не
а
Примеры использования и результаты
Ну и напоследок несколько примеров использования модели векторного пространства на практике.
Впервые я столкнулся с ней в приложении для фильтрации спама. Программа использовала метод LSA и при обучающей выборке размером 30% от всего набора тестов выдавала порядка 99% правильных решений.
Следующая моя встреча с VSM произошла уже на моём собственном проекте. Суть проекта была в организации системы управления коллекциями документов. Изначально планировалось использовать Random Indexing для добавления функции семантического поиска, но в последствие акцент сместился на автоматическую сортировку по коллекциям – большое количество документов загружалось автоматически, и ручное тегирование по темам было слишком трудоёмкой задачей. При ручном формировании набора документов для каждой из корзин метод показал результаты по 92-96%, при этом, двигая пороговое значение, можно было добиться практически полного отсутствия как ложно положительных, так и ложно отрицательных ответов.
Немного нестандартным приложением семантических технологий для меня стал проект по вычислению Skill Rank – ранга навыков пользователей. Суть заключалась в том, чтобы анализировать профили людей на известных сайтах социальных сетей (таких как Facebook и LinkedIn) и вычислять уровень их знаний в той или иной области. Тот же подход может быть использован менеджерами по персоналу для поиска наиболее компетентных работников.
Довольно интересной мне показалась идея Content Addressable Networks (CAN) – сетей, адресуемых контентом. В таких сетях физическим адресам серверов сопоставляются вектора всё той же VSM. Текст, приходящий на центральный сервер, перенаправляется для хранения на тот сервер, к которому оказался ближе всего по смыслу. При поиске же запрос не приходится сравнивать со всеми документами – достаточно сначала найти наиболее близкий к запросу узел сети, а затем искать наиболее релевантные документы только в рамках этого узла.
Ну и, наконец, благодаря близости классификации к теории нечётких множеств есть возможность использовать большинство соответствующих методов, а это различные модели управления, приближённые рассуждения и всевозможные нечёткие алгоритмы.
Список литературы:
1 — если быть более точным, то данная модель называется моделью пространства слов (word space model), что гораздо точнее характеризует основную идею, а именно выражение каждого слова в виде вектора в многомерном пространстве. Однако выражение «модели векторного пространства» (vector space model) встречается чаще, поэтому я буду использовать его;
2 — интересен тот факт, что учёный, разработавший этот метод, — Magnus Sahlgren – является по совместительству Шведским музыкантом, играющим в стиле «метал».
Введение, или Who is who?
Чтобы не произошло путаницы, сразу же сделаю пояснение. Существует два основных подхода к семантическому поиску, да и вообще к сравнению документов по смыслу. Первый подход основан на ручном наделении объектов некоторыми атрибутами и обработке именно атрибутов, а не самих объектов. Сюда можно отнести тегирование, ручную каталогизацию, онтологии и, конечно же, концепцию Web 3.0. Суть всегда одна и та же – большое количество людей создаёт базу знаний, то есть набор триплетов <субъект, предикат, объект>, плюс, в некоторых случаях, правила вывода. Иногда, правда, процесс извлечения знаний пытаются автоматизировать. Так, например, существуют системы, строящие триплеты по предложениям на естественных языках. Грубо говоря, из предложения «12 апреля 1953 года состоялось бракосочетание сенатора Кеннеди и Жаклин Бувье» такая система способна вывести логическую связку <Джон_Кеннеди, женат_на, Жаклин_Бувье>. Однако создание и развитие таких систем всё ещё требует большого количества ручной работы, причём работы не простых пользователей или верстальщиков, а профессиональных программистов и лингвистов.
Второй подход, о котором и пойдёт речь, основан на противоположной идее: вместо сложных логических правил используется простая математическая модель, вместо тысяч часов ручной работы – статистический анализ уже существующих текстов. Начало этот подход берёт в работах над методом LSA (Latent Semantic Analysis, неявный семантический анализ). Позже метод претерпел множество модификаций и получил довольно широкую известность. Достаточно сказать, что сегодня Google и ряд других крупных поисковиков используют один из параметров данного метода (а именно так называемый индекс tf*idf) при ранжировании результатов.
Итак, в чём же суть подхода, и какие существуют методы для его реализации?
LSA, или Статистика не всегда врёт
Основная идея проста до безобразия: чем чаще два слова встречаются в одних и тех же контекстах (документах), тем ближе они по смыслу. Действительно, можно ожидать, что слова «программирование» и «алгоритм» будут встречаться в одних и тех же документах гораздо чаще, чем, например, «программирование» и «собаководство». Для LSA частота встречаемости в конкретном документе зачастую представляется как раз в виде индекса tf*idf, что расшифровывается как «term frequency * inverse document frequency». Term frequency – частота термина – рассчитывается как количество вхождений конкретного термина в конкретный документ, делённое на общее количество слов в этом документе:
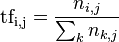
Document frequency – частота документа – это количество документов, в которых данный термин встречается, делённое на общее количество документов. Inverse document frequency, соответственно, это величина, обратная document frequency, то есть idf = 1/df. Обычно, чтобы как-то смягчить эффект действия idf на общий результат, вместо самого значения берётся его логарифм:
В общем-то, индекс tf*idf уже можно использовать для ранжирования результатов поиска – чем выше индекс, тем больше релевантность данного термина в данном документе. Тем не менее, для более сложных задач, таких как сравнение двух документов, этого всё ещё не достаточно.
Все индексы tf*idf для всех терминов и всех документов можно занести в единую таблицу:
Заголовки строк матрица – термины, заголовки столбцов – документы. Элементы самой матриц будем называть «веса». Каждая строка представляет собой распределение индексов терминов по документам, каждый столбец – распределение документов по терминам, то есть получается взаимное выражение терминов через документы, в которых они встречаются, и документов через термины, из которых они состоят, поэтому все законы, применимые для сравнения терминов будут также работать и для сравнения целых документов. Для простоты и краткости изложения далее при описании данного метода я буду говорить только про распределение терминов.
Авторы LSA предположили, что два термина будут тем более похожи по смыслу, чем ближе будут соответствующие строки нашей матрицы (вспомните пример про программирование-алгоритм-собаководство). Меру схожести двух строк можно измерять различными способами, например, с помощью поэлементной разницы.
Остаётся одна проблема – размер матрицы. Если мы работаем с более или менее крупным корпусом текстов, то количество терминов будет измеряться в тысячах и десятках тысяч, а про документы и говорить не стоит. Даже просто держать такую матрицу в памяти крайне накладно, а поиск похожих терминов – это жесточайший удар по производительности системы. Чтобы решить эту проблему, было решено редуцировать матрицу, то есть уменьшать её размер до приемлемого.
Естественно, при уменьшении ранга матрицы желательно сохранить наиболее «важные» её элементы, то есть те, которые образуют базис соответствующего пространства. Самым эффективным методом для решения этой задачи считается сингулярное разложение (Singular Value Decomposition, SVD). Его описание можно найти здесь.
К сожалению, при всей своей математической эффективности SVD не решает проблемы с памятью, поскольку перед применением алгоритма редуцирования всё ещё требуется загрузка полной начальной матрицы. Кроме того, каждый раз при добавлении документа всю процедуру необходимо повторять.
Random Indexing, или Неслучайна случайность
Сделаем шаг назад и посмотрим на всю картину целиком. У нас есть предположение, что слова, встречающиеся в одних и тех же контекстах (документах), а также контексты (документы), содержащие одни и те же слова, являются близкими по смыслу. Информацию о совместной встречаемости можно организовать в виде матрицы или, что то же самое, в виде набора векторов в некотором многомерном пространстве. Например, если взять матрицу, которую мы строили для LSA, то её строки будут представлять собой T векторов в D-мерном пространстве, где T – количество терминов, а D, соответственно, — количество документов. Это и составляет суть моделей векторного пространства1. Чтобы как-то различать документы, необходим некий способ уникально представить каждый из них в виде вектора. Простейший способ осуществить это – сделать их все ортогональными, то есть построить на их основе единичную матрицу:
d’1 = [1, 0, 0, 0, 0, …]
d’2 = [0, 1, 0, 0, 0, …]
d’3 = [0, 0, 1, 0, 0, …]
…
Тогда позиция единицы в векторе будет однозначно идентифицировать документ.
Здесь мы возвращаемся к проблеме потребления памяти и уменьшению ранга матрицы (количества измерений). Нам всё ещё необходимо уникально представить каждый документ, однако использовать для этого не D измерений, а гораздо меньше.
К счастью оказалось, что в многомерном пространстве гораздо больше почти ортогональных направлений, чем действительно ортогональных. Это значит, что мы можем аппроксимировать нашу единичную матрицу просто заменив единственные ненулевые элементы в векторах наших документов набором из нескольких ненулевых элементов на случайно выбранных позициях. То есть вместо представленной выше матрицы мы получим что-то вроде:
d’1 = [1, 0, 0, …, 0, 1, 0, …, 0, 0, 0]
d’2 = [0, 0, 0, …, 1, 0, 0, …, 0, 0, 1]
d’3 = [0, 0, 1, …, 0, 0, 0, …, 0, 1, 0]А это именно то, что нам и нужно. Важной особенностью здесь является тот факт, что при добавлении новых документов нет необходимости увеличивать размерность векторов всех документов, то есть длина векторов остаётся фиксированной.
О’кей, мы получили способ уникально представлять документы в векторном пространстве. Что дальше? А дальше нам необходимо выразить термины через документы, в которых они встречаются.
В LSA мы использовали вектора (строки матрицы), составленные из значений некоторой функции частоты встречаемости (в примере выше – это tf*idf). Каждый из этих элементов можно разложить на элементы, представив в виде суммы ортогональных векторов, т.е., например, вектор:
[0.21, 0.05, 0, 0.38, 0.29, …]можно представить в виде:
[0.21, 0, 0, 0, 0, …] + [0, 0.05, 0, 0, 0, …] + [0, 0, 0, 0, 0, …] + [0, 0, 0, 0.38, 0, …] + [0, 0, 0, 0, 0.29, ….] + …Каждое из слагаемых – это вектор, уникально характеризующий документ, умноженный на значение функции частоты текущего термина. То есть, с математической точки зрения термин можно выразить через содержащие его документы просто сложив вектора этих самых документов (с учётом частоты, разумеется). И в данном случае не имеет значения, являются ли вектора документов действительно ортогональным (как в LSA) или почти ортогональными.
Таким образом, вектор термина будет равен:
где
Частота здесь может рассчитываться просто как количество вхождений данного термина в документ. В данном случае нормализация частоты не требуется (об этом ниже), поэтому храниться и обрабатываться будут целые числа.
Обратите внимание, что размер векторов t уже не зависит от количества документов в корпусе – он всегда фиксирован и равен тому значению, которое мы задали для начальных векторов документа.
Ну и последний момент. Слова сравнивать по смыслу, конечно, интересно, но непрактично. Сравнивать нам нужно тексты, т. е. документы. И тут закономерный вопрос – как выразить документы через содержащиеся в них слова? Ответ: точно так же, как и слова через документы: сложив вектора соответствующих объектов:
где
Ещё раз: мы случайным образом генерируем начальные вектора для документов (d’), затем на их основе рассчитываем вектора всех терминов (t), и уже из них получаем окончательные вектора документов (d).
Описанный выше метод носит название Random Indexing (примерный перевод – «индексирование случайными числами»)2.
Так что же дают векторные представления документов?
Во-первых, их можно сравнивать. Два вектора будут тем ближе, чем меньше угол между ними. Для оценки угла достаточно взять любую монотонно-возрастающую функцию, например, косинус:
Произведение векторов
Во-вторых, что не менее важно, над ними можно проводить все те же операции, что и над обычными векторами – сложение, вычитание и даже умножение на скаляр. Нетрудно догадаться, как будут интерпретироваться эти операции: сложение – это просто объединение двух текстов, умножение на скаляр – повторение одного и того же текста несколько раз и т. д.
Классификация, или Мальчики налево, девочки направо
Как только в систему введена мера близости двух объектов, можно начинать использовать алгоритмы классификации и кластеризации. Кластеризация, то есть классификация по заранее неизвестным классам, — тема насколько интересная, настолько и большая, поэтому и требующая отдельной статьи. Здесь же остановимся только на классификации.
Классификация – это отнесение объекта (в нашем случае текста) к одному из предопределённых классов. Чтобы не возникло путаницы с терминологией, будем называть эти классы корзинами. Каждая корзина представляет собой просто вектор. Это может быть вектор конкретного термина (например, «математика»), канонического документа (конспект лекций по математике) или набора документов. Степень близости текста и корзины определяется всё тем же косинусом (или любой другой функцией расстояния) между векторами этих объектов.
Есть два основных типа классификации:
- классификация в одну из множества корзин;
- классификация в несколько корзин.
К первому типу относятся, например, фильтры спама: письмо так или иначе должно быть классифицировано в одну из двух папок – Inbox или Spam. Классификация проводится просто сравнением косинусов для всех доступных корзин – где значение больше, туда и классифицируем.
Чуть сложнее обстоит дело с классификацией в несколько корзин. Наиболее полно модель классификации на множество классов описывает теория нечётких множеств.
Классическая теория множеств имеет дело с бинарным признаком вхождения – некий объект либо входит, либо не входит во множество. Нечёткие же множества позволяют градуировать степень вхождения (принадлежности). Например, можно сказать: «данный объект принадлежит данному множеству со степенью 0.7».
Для оценки степени принадлежности используется, как нетрудно догадаться, функция принадлежности. И вот тут мы видим полное соответствие задаче классификации – корзины можно рассматривать как множества, классифицируемые тексты – как объекты, а в качестве функции принадлежности используется функция близости векторов.
Если необходимо бинарно определить, принадлежит ли текст некоторой корзине, используется пороговое значение. Значение это может быть как постоянным, так и плавающим.
В качестве примера модели классификации с плавающим значением рассмотрим улучшение обычной классификации с использованием деревьев. Если некую область знаний можно описать как иерархию понятий, то эту область возможно представить в виде дерева с большим количеством ветвей. Например, понятие «наука» может является корнем и иметь детей «физика», «химия», «математика», понятие «математика», в свою очередь, может является родителем для «теория чисел», «теория множеств», «планиметрия» и т.д. Построение такого дерева начинается снизу – листья формируются из реальных текстов по указанной теме, а узлы представляют собой просто сумму векторов всех своих детей. Так, например, «математика» — это «теория множеств» + «теория чисел» + «планиметрия», а «наука» — это сумма всех научных направлений.
Классификация производится рекурсивно: вначале проверяется, может ли данный текст быть отнесён к текущему корню, и если да, то ссылка на эту корзину сохраняется (аккумулируется), а процедура повторяется для всех детей. Выигрыш здесь не только в возможности обобщения понятий, но и в производительности – если линейная классификация занимала O(n) времени, то иерархическая – всего лишь около O(log n).
Проблема здесь состоит в том, что длины векторов корня и листьев сильно отличаются, и при фиксированном пороге вхождения текст может просто «не дойти» до листьев, остановившись ещё на корне. Чтобы этого не произошло, пороговое значение должно быть плавающим и представлять собой функцию от длины вектора корзины. В зависимости от задачи это может быть константа, делённая либо на длину вектора, либо на какое то «смягчённое» значение, например, корень квадратный из этой самой длины.
Реализация, или Сделай сам
Когда я только начинал заниматься этой темой, был сильно удивлён, что не смог найти приемлемой библиотеки для реализации VSM на целевой платформе (на тот момент это была JVM). Всё, что мне удалось отыскать, – это либо готовые
Во-первых, алгоритм активно использует информацию о частоте слов, а также требует синтаксического и морфологического разбора входных текстов. То есть использует всё то же, что и поисковые движки. Поэтому в качестве базы для реализации модели лучше всего использовать именно их. Одной из лучших свободных реализаций поискового движка является Lucene. Сам по себе Lucene написан на Java, однако существует огромное количество портов на другие языки и платформы, в том числе .NET, С++, Delphi, Python, Ruby и многие другие.
Во-вторых, представление векторов, использованное в данной статье для Random Indexing, является не совсем верным и совсем неэффективным. В примере вектора имели бинарные элементы – либо 0 (большинство), либо 1. На самом деле более эффективно использовать тринарные элементы: -1, 0 или 1. Знак ненулевых элементов выбирается, так же как и позиция, случайно.
Поскольку вектора сильно разряжённые (я использовал 2-20 ненулевых значений для векторов длиной 5000-1000 элементов), то их намного эффективней представлять не в виде единого вектор, хранящего и единицы, и нули, а список пар. То есть не
[1, 0, 0, …, 0, 1, 0, …, 0, 0, 0]а
[[0, 1], [294, -1], …, [4116, -1]]Примеры использования и результаты
Ну и напоследок несколько примеров использования модели векторного пространства на практике.
Впервые я столкнулся с ней в приложении для фильтрации спама. Программа использовала метод LSA и при обучающей выборке размером 30% от всего набора тестов выдавала порядка 99% правильных решений.
Следующая моя встреча с VSM произошла уже на моём собственном проекте. Суть проекта была в организации системы управления коллекциями документов. Изначально планировалось использовать Random Indexing для добавления функции семантического поиска, но в последствие акцент сместился на автоматическую сортировку по коллекциям – большое количество документов загружалось автоматически, и ручное тегирование по темам было слишком трудоёмкой задачей. При ручном формировании набора документов для каждой из корзин метод показал результаты по 92-96%, при этом, двигая пороговое значение, можно было добиться практически полного отсутствия как ложно положительных, так и ложно отрицательных ответов.
Немного нестандартным приложением семантических технологий для меня стал проект по вычислению Skill Rank – ранга навыков пользователей. Суть заключалась в том, чтобы анализировать профили людей на известных сайтах социальных сетей (таких как Facebook и LinkedIn) и вычислять уровень их знаний в той или иной области. Тот же подход может быть использован менеджерами по персоналу для поиска наиболее компетентных работников.
Довольно интересной мне показалась идея Content Addressable Networks (CAN) – сетей, адресуемых контентом. В таких сетях физическим адресам серверов сопоставляются вектора всё той же VSM. Текст, приходящий на центральный сервер, перенаправляется для хранения на тот сервер, к которому оказался ближе всего по смыслу. При поиске же запрос не приходится сравнивать со всеми документами – достаточно сначала найти наиболее близкий к запросу узел сети, а затем искать наиболее релевантные документы только в рамках этого узла.
Ну и, наконец, благодаря близости классификации к теории нечётких множеств есть возможность использовать большинство соответствующих методов, а это различные модели управления, приближённые рассуждения и всевозможные нечёткие алгоритмы.
Список литературы:
- S. Deerwester, S. T. Dumais. Indexing by Latent Semantic Analysis.
- M. Sahlgren. An Introduction to Random Indexing.
- И.С. Мисуно, Д.А. Рачковский. Поиск текстовой информации с помощью векторных представлений.
- Ch. Tang, Zh. Xu, S. Dwarkadas. Peer-to-Peer Information Retrieval Using
- Self-Organizing Semantic Overlay Networks.
- Д. А. Поспелов. Нечёткие множества в моделях управления и искусственного интеллекта.
1 — если быть более точным, то данная модель называется моделью пространства слов (word space model), что гораздо точнее характеризует основную идею, а именно выражение каждого слова в виде вектора в многомерном пространстве. Однако выражение «модели векторного пространства» (vector space model) встречается чаще, поэтому я буду использовать его;
2 — интересен тот факт, что учёный, разработавший этот метод, — Magnus Sahlgren – является по совместительству Шведским музыкантом, играющим в стиле «метал».