Статья появилась как попытка разобраться, имеет ли смысл вставлять SIMD инструкции в код ручками, или компилятор справится сам? Сразу скажу, что универсального ответа не получилось. Зато с картинками.
В рамках задачи кластеризации часто возникает необходимость найти расстояние междусферическими конями в вакууме точками в многомерном пространстве. По сути же, нам нужна функция, принимающая на вход два массива одинаковой длины и возвращать скаляр.
Как известно, для любого нормированного пространства можно взять в качестве функции расстояния норму разности двух его элементов и получить метрическое пространство. Далее по тексту будем оптимизировать расчет метрик, заданных нормами L1, L2, Max.
В первой и третьей функциях присутствуют только сложения и вычитания. В distL2 — умножение в цикле и корень. Вопрос на засыпку: какая функция выполняется дольше?
Ниже время выполнения функций на Core i3 M330. Длина векторов — 32. Количество вызовов — 2^27. Компилятор — Microsoft ® C/C++ (VS2010).
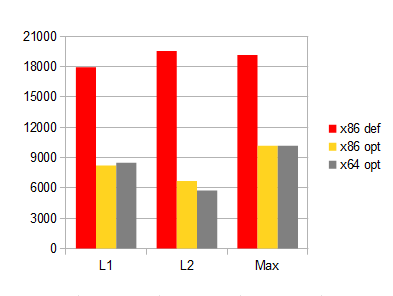
«x86 opt» отличается от «x86 def» включенными опциями "/arch:SSE2" и "/fp:fast".
Нетрудно заметить, что в оптимизированной версии, несмотря на умножения, самой быстрой оказалась distL2. Скорость выполнения получилась тем больше, чем меньше в функции ветвлений. Есть подозрение, что distL1 и distMax можно ускорить. Попробуем.
Как нетрудно догадаться из заголовка, будем ускоряться при помощи библиотеки IPP от Intel (использовалась версия 6.1.1). Пару часов общения с ней (полтора из которых — прикручивание к проекту) дают следующие результаты.
Две другие функции будут различаться только суффиксом ippsNorm: "_L2", "_Inf" вместо "_L1". Код выглыдит еще проще и красивей, чем в оригинальном варианте. Однако, есть проблема: необходимо выделять промежуточный массив. Делать это при каждом вызове функции нельзя из соображений производительности. Использовать статический указатель (читай Singleton) — значит забыть о многопоточности. Проблема решаема, но о ней лучше знать заранее.
Ну и наконец, способ, выведенный в название статьи — векторизация «вручную». Современные компиляторы позволяют осуществлять доступ к некоторым инструкциям процессора посредством вызова псевдо-функций. Это так называемые intrinsic-и. Их объявления есть в файлах mmintrin.h, xmmintrin.h, emmintrin.h. Ниже — моя реализация расчета метрик на их основе.
Читаемость кода ниже среднего. И вряд ли ее можно сильно улучшить. Если в двух словах, помимо векторизации, суть тут в возможности уйти от ветвления:
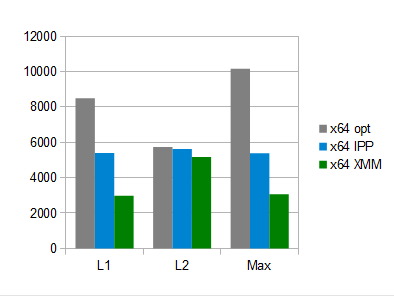
Как можно видеть, функции distL1 и distMax удалось ускорить в разы. В то же время, выигрыш для distL2 составил всего 10%. Основной бонус — производительность, не зависящая от флагов компилятора.
Надеюсь, информация оказалась полезной.
Задача
В рамках задачи кластеризации часто возникает необходимость найти расстояние между
Как известно, для любого нормированного пространства можно взять в качестве функции расстояния норму разности двух его элементов и получить метрическое пространство. Далее по тексту будем оптимизировать расчет метрик, заданных нормами L1, L2, Max.
Реализация в лоб
float distL1(const float* x, const float* y, unsigned size)
{
float dist = 0.0f;
for (unsigned i=0; i<size; ++i) {
float dx = x[i]-y[i];
if (dx>0)
dist += dx;
else
dist -= dx;
}
return dist;
}
float distL2(const float* x, const float* y, unsigned size)
{
float dist = 0.0f;
for (unsigned i=0; i<size; ++i) {
float d = x[i]-y[i];
dist += d*d;
}
return sqrtf(dist);
}
float distMax(const float* x, const float* y, unsigned size)
{
float dist = 0.0f;
for (unsigned i=0; i<size; ++i) {
float dx = x[i]-y[i];
if (dx<0)
dx = -dx;
if (dx>dist)
dist = dx;
}
return dist;
}В первой и третьей функциях присутствуют только сложения и вычитания. В distL2 — умножение в цикле и корень. Вопрос на засыпку: какая функция выполняется дольше?
Ниже время выполнения функций на Core i3 M330. Длина векторов — 32. Количество вызовов — 2^27. Компилятор — Microsoft ® C/C++ (VS2010).

«x86 opt» отличается от «x86 def» включенными опциями "/arch:SSE2" и "/fp:fast".
Нетрудно заметить, что в оптимизированной версии, несмотря на умножения, самой быстрой оказалась distL2. Скорость выполнения получилась тем больше, чем меньше в функции ветвлений. Есть подозрение, что distL1 и distMax можно ускорить. Попробуем.
Реализация с Intel Integrated Performance Primitives
Как нетрудно догадаться из заголовка, будем ускоряться при помощи библиотеки IPP от Intel (использовалась версия 6.1.1). Пару часов общения с ней (полтора из которых — прикручивание к проекту) дают следующие результаты.
namespace IPP
{
using namespace ThreadLS;
float distL1(const float* x, const float* y, unsigned size)
{
float dist;
float* pBuf = ThreadBuf::get(size);
ippsSub_32f(x, y, pBuf, size);
ippsNorm_L1_32f(pBuf, size, &dist);
return dist;
}
// ...
}Две другие функции будут различаться только суффиксом ippsNorm: "_L2", "_Inf" вместо "_L1". Код выглыдит еще проще и красивей, чем в оригинальном варианте. Однако, есть проблема: необходимо выделять промежуточный массив. Делать это при каждом вызове функции нельзя из соображений производительности. Использовать статический указатель (читай Singleton) — значит забыть о многопоточности. Проблема решаема, но о ней лучше знать заранее.
Intrinsics
Ну и наконец, способ, выведенный в название статьи — векторизация «вручную». Современные компиляторы позволяют осуществлять доступ к некоторым инструкциям процессора посредством вызова псевдо-функций. Это так называемые intrinsic-и. Их объявления есть в файлах mmintrin.h, xmmintrin.h, emmintrin.h. Ниже — моя реализация расчета метрик на их основе.
namespace XMM
{
typedef __m128 (*xmm_func)(__m128 , __m128 );
__m128 add_ps(__m128 a, __m128 b) { return _mm_add_ps(a, b); };
__m128 max_ps(__m128 a, __m128 b) { return _mm_max_ps(a, b); };
__m128 delta_abs(__m128 x4, __m128 y4)
{
__m128 max = _mm_max_ps(x4, y4);
__m128 min = _mm_min_ps(x4, y4);
return _mm_sub_ps(max, min);
}
__m128 delta_sqr(__m128 x4, __m128 y4)
{
__m128 sub = _mm_sub_ps(x4, y4);
return _mm_mul_ps(sub, sub);
}
__m128 sse_dist(const float* x, const float* y, unsigned size,
xmm_func delta, xmm_func accum)
{
__m128 acc4 = _mm_setzero_ps();
for (unsigned i=0; i<(size>>2); ++i, x+=4, y+=4) {
__m128 x4 = _mm_loadu_ps(x);
__m128 y4 = _mm_loadu_ps(y);
acc4 = accum(acc4, delta(x4, y4));
}
unsigned tail = size & 0x3;
if (tail) {
__m128 x4 = _mm_setzero_ps();
__m128 y4 = _mm_setzero_ps();
for (unsigned i=0; i<tail; ++i, ++x, ++y) {
x4.m128_f32[i] = *x;
y4.m128_f32[i] = *y;
}
acc4 = accum(acc4, delta(x4, y4));
}
return acc4;
}
float distL1(const float* x, const float* y, unsigned size)
{
__m128 sum4 = sse_dist(x, y, size, delta_abs, add_ps);
for (char i=1; i<4; ++i)
sum4.m128_f32[0] += sum4.m128_f32[i];
return sum4.m128_f32[0];
}
float distL2(const float* x, const float* y, unsigned size)
{
__m128 sum4 = sse_dist(x, y, size, delta_sqr, add_ps);
for (char i=1; i<4; ++i)
sum4.m128_f32[0] += sum4.m128_f32[i];
sum4 = _mm_sqrt_ss(sum4);
return sum4.m128_f32[0];
}
float distMax(const float* x, const float* y, unsigned size)
{
__m128 max4 = sse_dist(x, y, size, delta_abs, max_ps);
float dist = max4.m128_f32[0];
for (char i=1; i<4; ++i) {
float cur = max4.m128_f32[i];
if (cur > dist)
dist = cur;
}
return dist;
}
}Читаемость кода ниже среднего. И вряд ли ее можно сильно улучшить. Если в двух словах, помимо векторизации, суть тут в возможности уйти от ветвления:
|x-y|=max{x,y}-min{x,y}.Результаты

Как можно видеть, функции distL1 и distMax удалось ускорить в разы. В то же время, выигрыш для distL2 составил всего 10%. Основной бонус — производительность, не зависящая от флагов компилятора.
Надеюсь, информация оказалась полезной.