В данной статье приводится доступный теоретический обзор сверточных нейронных сетей (Convolutional Neural Network, CNN) и разъясняется их применение к задаче классификации изображений.

Термин «обработка изображений» относится к широкому классу задач, входными данными для которых являются изображения, а выходными могут быть как изображения, так и наборы связанных с ними характерных признаков. Существует множество вариантов: классификация, сегментация, аннотирование, обнаружение объектов и т. п. В данной статье мы исследуем классификацию изображений не только потому, что это самая простая задача, но и потому, что она лежит в основе многих других задач.
Общий подход к задаче классификации изображений состоит из следующих двух шагов:
Общепринятая последовательность операций использует поверх созданных вручную признаков такие простые модели, как многоуровневое восприятие (MultiLayer Perceptron, MLP), машина векторов поддержки (Support Vector Machine, SVM), метод k ближайших соседей и логистическая регрессия. Признаки генерируются с использованием различных трансформаций (например, перевод в оттенки серого и определение порогов) и дескрипторов, например, гистограммы ориентированных градиентов (Histogram of Oriented Gradients, HOG) или трансформации масштабно-инвариантных признаков (Scale-Invariant Feature Transform, SIFT), и т. п.
Основным ограничением общепринятых методов является участие эксперта, выбирающего набор и последовательность шагов для генерации признаков.
Со временем было замечено, что большинство техник генерации признаков можно обобщить, используя ядра (фильтры) — небольшие матрицы (обычно размера 5 × 5), являющиеся свертками исходных изображений. Свертку можно рассматривать как последовательный двухступенчатый процесс:
Результат свертки изображения и ядра называется картой признаков.
Математически более строгое объяснение приведено в соответствующей главе недавно вышедшей книги «Глубокое обучение», И. Гудфеллоу (I. Goodfellow), И. Бенджио (Y. Bengio) и А. Курвиля (A. Courville).
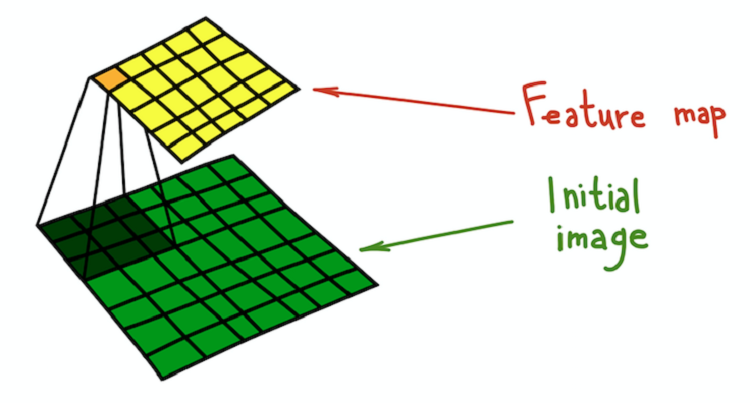
Процесс свертки ядра (темно-зеленый) с исходным изображением (зеленый), в результате которого получается карта признаков (желтый).
Простой пример трансформации, которую можно произвести при помощи фильтров — это размытие изображения. Возьмем фильтр, состоящий из всех единиц. Он рассчитывает среднее значение по окрестности, определяемой фильтром. В данном случае окрестность представляет собой квадратный участок, но он может быть крестообразным или каким угодно еще. Усреднение ведет к потере информации о точном положении объектов, размывая, таким образом, все изображение. Подобное интуитивное объяснение можно привести для любого фильтра, созданного вручную.

Результат свертки изображения здания Гарвардского университета с тремя разными ядрами.
Сверточный подход к классификации изображений имеет ряд существенных недостатков:
К счастью, были изобретены обучаемые фильтры, которые представляют собой базовый принцип, лежащий в основе CNN. Принцип прост: Будем обучать фильтры, применяемые к описанию изображений, с целью наилучшего выполнения ими своей задачи.
У CNN нет одного изобретателя, но один из первых случаев их применения — это LeNet-5* в работе «Применение градиентного обучения к задаче распознавания документов» (Gradient-based Learning Applied to Document Recognition) И. ЛеКуна (Y. LeCun) и других авторов.
CNN убивают сразу двух зайцев: нет необходимости в предварительном определении фильтров, и процесс обучения становится сквозным. Типовая архитектура CNN состоит из следующих частей:
Рассмотрим каждую часть подробнее.
Сверточный слой представляет собой основной структурный элемент CNN. Сверточный слой обладает набором характеристик:
Локальная (разреженная) связность. В плотных слоях каждый нейрон соединен с каждым нейроном предыдущего слоя (поэтом их и назвали плотными). В сверточном слое каждый нейрон соединен лишь с небольшой частью нейронов предыдущего слоя.
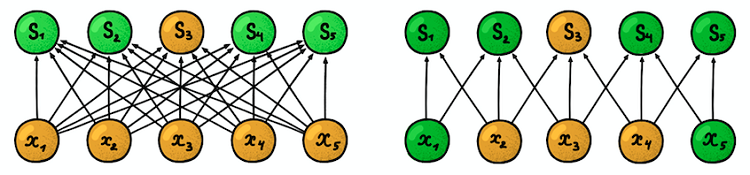
Пример одномерной нейросети. (слева) Соединение нейронов в типовой плотной сети, (справа) Характеристика локальной связности, присущая сверточному слою. Изображения взяты из книги «Глубокое обучение» (Deep Learning) И. Гудфеллоу (I. Goodfellow) и других авторов
Размер участка, с которым соединен нейрон, называется размером фильтра (длиной фильтра в случае одномерных данных, например, временных серий, или шириной/высотой в случае двумерных данных, например, изображений). На рисунке справа размер фильтра равен 3. Веса, с которыми осуществляется соединение, называются фильтром (вектором в случае одномерных данных и матрицей для двумерных). Шаг — это расстояние, на которое фильтр перемещается по данным (на рисунке справа шаг равен 1). Идея локальной связности представляет собой не что иное, как ядро, перемещающееся на некоторый шаг. Каждый нейрон сверточного уровня представляет и реализует одно конкретное положение ядра, скользящего по исходному изображению.
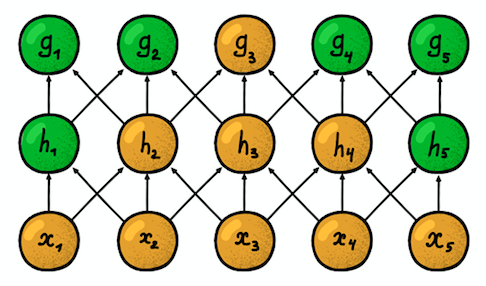
Два соседних одномерных сверточных слоя
Еще одно важное свойство — так называемая зона восприимчивости. Она отражает количество позиций исходного сигнала, которые может «видеть» текущий нейрон. Например, зона восприимчивости первого слоя сети, показанной на рисунке, равна размеру фильтра 3, так как каждый нейрон соединен только с тремя нейронами исходного сигнала. Однако, на втором слое зона восприимчивости уже равна 5, так как нейрон второго слоя агрегирует три нейрона первого слоя, каждый из которых имеет зону восприимчивости 3. С ростом глубины зона восприимчивости растет линейно.
Разделяемые параметры. Напомним, что в классической обработке изображений одно и то же ядро скользило по всему изображению. Здесь применяется та же идея. Зафиксируем только размер фильтра весовых коэффициентов для одного слоя и будем применять эти весовые коэффициенты ко всем нейронам в слое. Это равносильно скольжению одного и того же ядра по всему изображению. Но может возникнуть вопрос: как мы можем чему-то обучиться с таким малым количеством параметров?

Темные стрелки представляют собой одинаковые весовые коэффициенты. (слева) Обычная MLP, где каждый весовой коэффициент представляет собой отдельный параметр, (справа) Пример разделения параметров, где несколько весовых коэффициентов указывают на один и тот же параметр обучения
Пространственная структура. Ответ на этот вопрос прост: будем обучать несколько фильтров в одном слое! Они размещаются параллельно друг другу, формируя, таким образом, новое измерение.
Приостановимся ненадолго и объясним представленную идею на примере двумерного RGB-изображения 227 × 227. Заметим, что здесь мы имеем дело с трехканальным входным изображением, что, по сути, означает, что у нас три входных изображения или трехмерные входные данные.

Пространственная структура входного изображения
Будем рассматривать размерности каналов как глубину изображения (заметим, что это не то же, что глубина нейросетей, которая равна количеству слоев сети). Вопрос состоит в том, как определить ядро для этого случая.
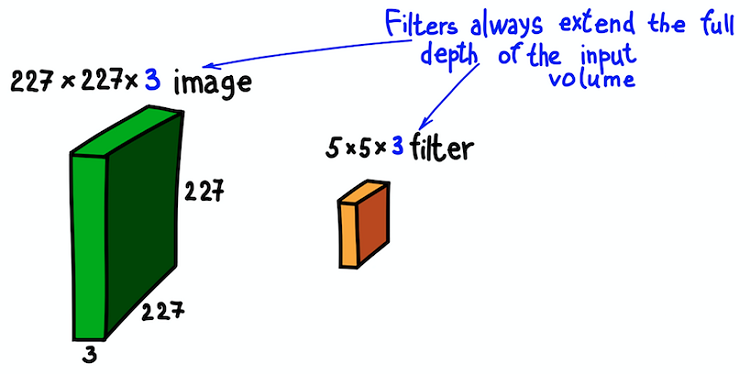
Пример двумерного ядра, по сути представляющего собой трехмерную матрицу с дополнительным измерением глубины. Этот фильтр дает свертку с изображением; то есть, скользит по изображению в пространстве, рассчитывая скалярные произведения
Ответ прост, хотя все еще не очевиден: сделаем ядро также трехмерным. Первые два измерения останутся прежними (ширина и высота ядра), а третье измерение всегда равно глубине входных данных.
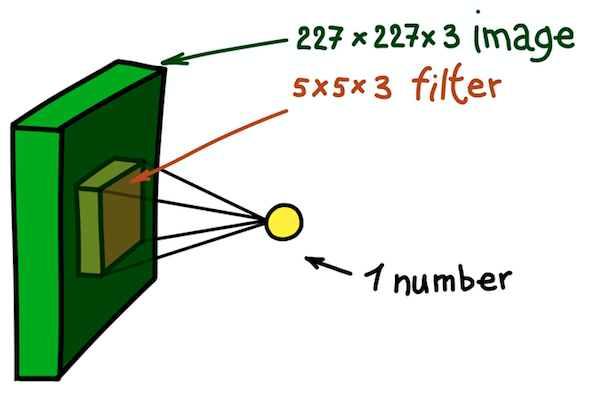
Пример пространственного шага свертки. Результатом скалярного произведения фильтра и небольшого участка изображения 5 × 5 × 3 (т. е. 5 × 5 × 5 + 1 = 76 размерность скалярного произведения + сдвиг) является одним числом
В данном случае весь участок 5 × 5 × 3 исходного изображения трансформируется в одно число, а само трехмерное изображение будет трансформировано в карту признаков (активационную карту). Карта признаков представляет собой набор нейронов, каждый из которых рассчитывает свою собственную функцию с учетом двух основных принципов, рассмотренных выше: локальной связности (каждый нейрон связан лишь с малой частью входных данных) и разделением параметров (все нейроны используют один и тот же фильтр). В идеале эта карта признаков будет такой же, как уже встречавшаяся нам в примере общепринятой сети — она хранит результаты свертки входного изображения и фильтра.
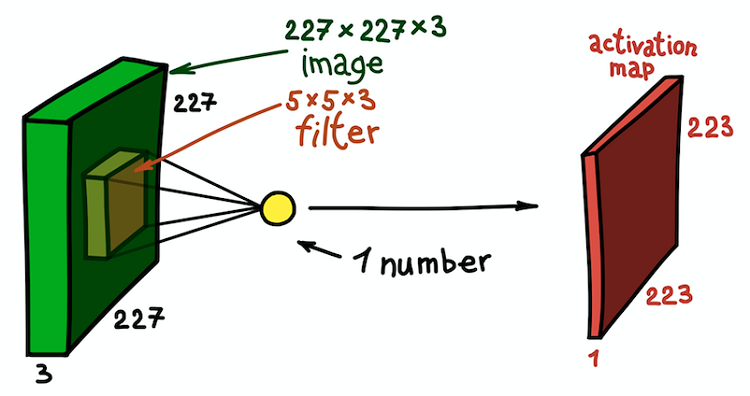
Карта признаков как результат свертки ядра со всеми пространственными положениями
Отметим, что глубина карты признаков равна 1, так как мы использовали только один фильтр. Но ничто не мешает нам использовать больше фильтров; например, 6. Все они будут взаимодействовать с одними и теми же входными данными и будут работать независимо друг от друга. Пройдем на один шаг дальше и совместим эти карты признаков. Их пространственные размеры одинаковы, поскольку одинаковы размеры фильтров. Таким образом, собранные вместе карты признаков можно рассматривать как новую трехмерную матрицу, размерность глубины которой представлена картами признаков от разных ядер. В этом смысле каналы RGB входного изображения есть не что иное, как три исходных карты признаков.
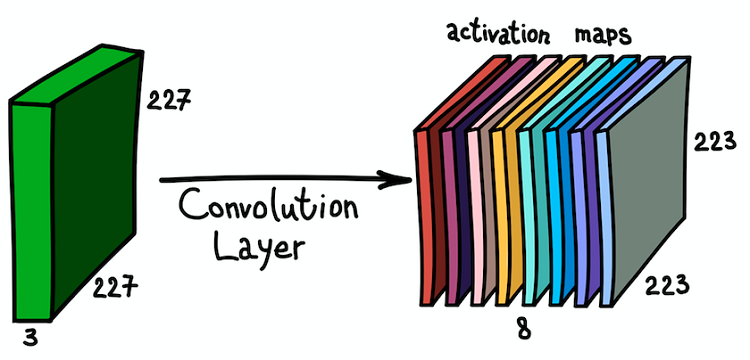
Параллельное применение нескольких фильтров к входному изображению и результирующее множество активационных карт
Такое понимание карт признаков и их совмещения очень важно, так как, осознав это, мы можем расширить архитектуру сети и устанавливать сверточные слои один поверх другого, увеличивая тем самым зону восприимчивости и обогащая свой классификатор.
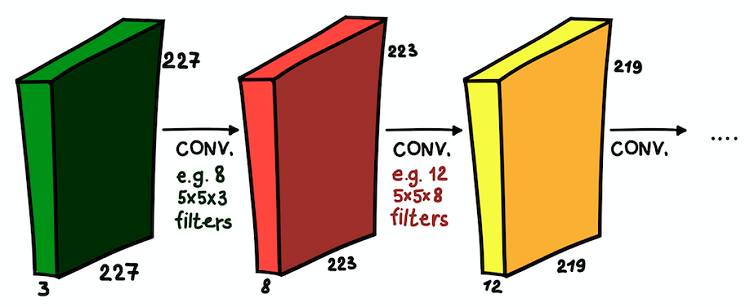
Сверточные слои, установленные поверх друг друга. В каждом слое размеры фильтров и их количество могут различаться
Теперь мы понимаем, что такое сверточная сеть. Основная цель этих слоев та же, что и при общепринятом подходе — обнаружить значимые признаки изображения. И, если в первом слое эти признаки могут быть очень простыми (наличие вертикальных/горизонтальных линий), с глубиной сети растет степень их абстракции (наличие собаки/кота/человека).
Сверточные слои являются основным структурным элементом CNN. Но существует еще одна важная и часто используемая часть — это слои подвыборки. В общепринятой обработке изображений нет прямого аналога, но подвыборку можно рассматривать как другой тип ядра. Что же это такое?

Примеры подвыборки. (слева) Как подвыборка меняет пространственные (но не канальные!) размеры массивов данных, (справа) Принципиальная схема работы подвыборки
Подвыборка фильтрует участок окрестности каждого пикселя входных данных определенной агрегирующей функцией, например, максимум, среднее и т. п. Подвыборка, по сути, есть то же, что и свертка, но функция комбинирования пикселей не ограничена скалярным произведением. Еще одно важное отличие — подвыборка работает только в пространственном измерении. Характерной чертой слоя подвыборки является то, что шаг, как правило, равен размеру фильтра (типовым значением является 2).
Подвыборка преследует три основных цели:
Сверточные слои и слои подвыборки служат одной цели — генерации признаков изображения. Завершающим шагом является классификация входного изображения на основе обнаруженных признаков. В CNN это делают плотные слои на вершине сети. Эта часть сети называется классификационной. Она может содержать несколько слоев поверх друг друга с полной связностью, но обычно заканчивается слоем класса softmax, активированным многопеременной логистической активационной функцией, в котором количество блоков равняется количеству классов. На выходе этого слоя находится распределение вероятностей по классам для входного объекта. Теперь изображение можно классифицировать, выбрав наиболее вероятный класс.

Общепринятый подход: без глубокого обучения
Термин «обработка изображений» относится к широкому классу задач, входными данными для которых являются изображения, а выходными могут быть как изображения, так и наборы связанных с ними характерных признаков. Существует множество вариантов: классификация, сегментация, аннотирование, обнаружение объектов и т. п. В данной статье мы исследуем классификацию изображений не только потому, что это самая простая задача, но и потому, что она лежит в основе многих других задач.
Общий подход к задаче классификации изображений состоит из следующих двух шагов:
- Генерация значимых признаков изображения.
- Классификация изображения на основе его признаков.
Общепринятая последовательность операций использует поверх созданных вручную признаков такие простые модели, как многоуровневое восприятие (MultiLayer Perceptron, MLP), машина векторов поддержки (Support Vector Machine, SVM), метод k ближайших соседей и логистическая регрессия. Признаки генерируются с использованием различных трансформаций (например, перевод в оттенки серого и определение порогов) и дескрипторов, например, гистограммы ориентированных градиентов (Histogram of Oriented Gradients, HOG) или трансформации масштабно-инвариантных признаков (Scale-Invariant Feature Transform, SIFT), и т. п.
Основным ограничением общепринятых методов является участие эксперта, выбирающего набор и последовательность шагов для генерации признаков.
Со временем было замечено, что большинство техник генерации признаков можно обобщить, используя ядра (фильтры) — небольшие матрицы (обычно размера 5 × 5), являющиеся свертками исходных изображений. Свертку можно рассматривать как последовательный двухступенчатый процесс:
- Пройти одним и тем же фиксированным ядром по всему исходному изображению.
- На каждом шаге рассчитать скалярное произведение ядра и исходного изображения в точке текущего нахождения ядра.
Результат свертки изображения и ядра называется картой признаков.
Математически более строгое объяснение приведено в соответствующей главе недавно вышедшей книги «Глубокое обучение», И. Гудфеллоу (I. Goodfellow), И. Бенджио (Y. Bengio) и А. Курвиля (A. Courville).

Процесс свертки ядра (темно-зеленый) с исходным изображением (зеленый), в результате которого получается карта признаков (желтый).
Простой пример трансформации, которую можно произвести при помощи фильтров — это размытие изображения. Возьмем фильтр, состоящий из всех единиц. Он рассчитывает среднее значение по окрестности, определяемой фильтром. В данном случае окрестность представляет собой квадратный участок, но он может быть крестообразным или каким угодно еще. Усреднение ведет к потере информации о точном положении объектов, размывая, таким образом, все изображение. Подобное интуитивное объяснение можно привести для любого фильтра, созданного вручную.

Результат свертки изображения здания Гарвардского университета с тремя разными ядрами.
Сверточные нейронные сети
Сверточный подход к классификации изображений имеет ряд существенных недостатков:
- Многоступенчатый процесс вместо сквозной последовательности.
- Фильтры являются отличным инструментом обобщения, но они представляют собой фиксированные матрицы. Как выбирать веса в фильтрах?
К счастью, были изобретены обучаемые фильтры, которые представляют собой базовый принцип, лежащий в основе CNN. Принцип прост: Будем обучать фильтры, применяемые к описанию изображений, с целью наилучшего выполнения ими своей задачи.
У CNN нет одного изобретателя, но один из первых случаев их применения — это LeNet-5* в работе «Применение градиентного обучения к задаче распознавания документов» (Gradient-based Learning Applied to Document Recognition) И. ЛеКуна (Y. LeCun) и других авторов.
CNN убивают сразу двух зайцев: нет необходимости в предварительном определении фильтров, и процесс обучения становится сквозным. Типовая архитектура CNN состоит из следующих частей:
- Сверточные слои
- Слои подвыборки
- Плотные (полносвязные) слои
Рассмотрим каждую часть подробнее.
Сверточные слои
Сверточный слой представляет собой основной структурный элемент CNN. Сверточный слой обладает набором характеристик:
Локальная (разреженная) связность. В плотных слоях каждый нейрон соединен с каждым нейроном предыдущего слоя (поэтом их и назвали плотными). В сверточном слое каждый нейрон соединен лишь с небольшой частью нейронов предыдущего слоя.

Пример одномерной нейросети. (слева) Соединение нейронов в типовой плотной сети, (справа) Характеристика локальной связности, присущая сверточному слою. Изображения взяты из книги «Глубокое обучение» (Deep Learning) И. Гудфеллоу (I. Goodfellow) и других авторов
Размер участка, с которым соединен нейрон, называется размером фильтра (длиной фильтра в случае одномерных данных, например, временных серий, или шириной/высотой в случае двумерных данных, например, изображений). На рисунке справа размер фильтра равен 3. Веса, с которыми осуществляется соединение, называются фильтром (вектором в случае одномерных данных и матрицей для двумерных). Шаг — это расстояние, на которое фильтр перемещается по данным (на рисунке справа шаг равен 1). Идея локальной связности представляет собой не что иное, как ядро, перемещающееся на некоторый шаг. Каждый нейрон сверточного уровня представляет и реализует одно конкретное положение ядра, скользящего по исходному изображению.

Два соседних одномерных сверточных слоя
Еще одно важное свойство — так называемая зона восприимчивости. Она отражает количество позиций исходного сигнала, которые может «видеть» текущий нейрон. Например, зона восприимчивости первого слоя сети, показанной на рисунке, равна размеру фильтра 3, так как каждый нейрон соединен только с тремя нейронами исходного сигнала. Однако, на втором слое зона восприимчивости уже равна 5, так как нейрон второго слоя агрегирует три нейрона первого слоя, каждый из которых имеет зону восприимчивости 3. С ростом глубины зона восприимчивости растет линейно.
Разделяемые параметры. Напомним, что в классической обработке изображений одно и то же ядро скользило по всему изображению. Здесь применяется та же идея. Зафиксируем только размер фильтра весовых коэффициентов для одного слоя и будем применять эти весовые коэффициенты ко всем нейронам в слое. Это равносильно скольжению одного и того же ядра по всему изображению. Но может возникнуть вопрос: как мы можем чему-то обучиться с таким малым количеством параметров?

Темные стрелки представляют собой одинаковые весовые коэффициенты. (слева) Обычная MLP, где каждый весовой коэффициент представляет собой отдельный параметр, (справа) Пример разделения параметров, где несколько весовых коэффициентов указывают на один и тот же параметр обучения
Пространственная структура. Ответ на этот вопрос прост: будем обучать несколько фильтров в одном слое! Они размещаются параллельно друг другу, формируя, таким образом, новое измерение.
Приостановимся ненадолго и объясним представленную идею на примере двумерного RGB-изображения 227 × 227. Заметим, что здесь мы имеем дело с трехканальным входным изображением, что, по сути, означает, что у нас три входных изображения или трехмерные входные данные.

Пространственная структура входного изображения
Будем рассматривать размерности каналов как глубину изображения (заметим, что это не то же, что глубина нейросетей, которая равна количеству слоев сети). Вопрос состоит в том, как определить ядро для этого случая.

Пример двумерного ядра, по сути представляющего собой трехмерную матрицу с дополнительным измерением глубины. Этот фильтр дает свертку с изображением; то есть, скользит по изображению в пространстве, рассчитывая скалярные произведения
Ответ прост, хотя все еще не очевиден: сделаем ядро также трехмерным. Первые два измерения останутся прежними (ширина и высота ядра), а третье измерение всегда равно глубине входных данных.

Пример пространственного шага свертки. Результатом скалярного произведения фильтра и небольшого участка изображения 5 × 5 × 3 (т. е. 5 × 5 × 5 + 1 = 76 размерность скалярного произведения + сдвиг) является одним числом
В данном случае весь участок 5 × 5 × 3 исходного изображения трансформируется в одно число, а само трехмерное изображение будет трансформировано в карту признаков (активационную карту). Карта признаков представляет собой набор нейронов, каждый из которых рассчитывает свою собственную функцию с учетом двух основных принципов, рассмотренных выше: локальной связности (каждый нейрон связан лишь с малой частью входных данных) и разделением параметров (все нейроны используют один и тот же фильтр). В идеале эта карта признаков будет такой же, как уже встречавшаяся нам в примере общепринятой сети — она хранит результаты свертки входного изображения и фильтра.

Карта признаков как результат свертки ядра со всеми пространственными положениями
Отметим, что глубина карты признаков равна 1, так как мы использовали только один фильтр. Но ничто не мешает нам использовать больше фильтров; например, 6. Все они будут взаимодействовать с одними и теми же входными данными и будут работать независимо друг от друга. Пройдем на один шаг дальше и совместим эти карты признаков. Их пространственные размеры одинаковы, поскольку одинаковы размеры фильтров. Таким образом, собранные вместе карты признаков можно рассматривать как новую трехмерную матрицу, размерность глубины которой представлена картами признаков от разных ядер. В этом смысле каналы RGB входного изображения есть не что иное, как три исходных карты признаков.

Параллельное применение нескольких фильтров к входному изображению и результирующее множество активационных карт
Такое понимание карт признаков и их совмещения очень важно, так как, осознав это, мы можем расширить архитектуру сети и устанавливать сверточные слои один поверх другого, увеличивая тем самым зону восприимчивости и обогащая свой классификатор.

Сверточные слои, установленные поверх друг друга. В каждом слое размеры фильтров и их количество могут различаться
Теперь мы понимаем, что такое сверточная сеть. Основная цель этих слоев та же, что и при общепринятом подходе — обнаружить значимые признаки изображения. И, если в первом слое эти признаки могут быть очень простыми (наличие вертикальных/горизонтальных линий), с глубиной сети растет степень их абстракции (наличие собаки/кота/человека).
Слои подвыборки
Сверточные слои являются основным структурным элементом CNN. Но существует еще одна важная и часто используемая часть — это слои подвыборки. В общепринятой обработке изображений нет прямого аналога, но подвыборку можно рассматривать как другой тип ядра. Что же это такое?

Примеры подвыборки. (слева) Как подвыборка меняет пространственные (но не канальные!) размеры массивов данных, (справа) Принципиальная схема работы подвыборки
Подвыборка фильтрует участок окрестности каждого пикселя входных данных определенной агрегирующей функцией, например, максимум, среднее и т. п. Подвыборка, по сути, есть то же, что и свертка, но функция комбинирования пикселей не ограничена скалярным произведением. Еще одно важное отличие — подвыборка работает только в пространственном измерении. Характерной чертой слоя подвыборки является то, что шаг, как правило, равен размеру фильтра (типовым значением является 2).
Подвыборка преследует три основных цели:
- Уменьшение пространственной размерности, или субдискретизация. Это делается для уменьшения количества параметров
- Рост зоны восприимчивости. За счет нейронов подвыборки в последующих слоях аккумулируется больше шагов входного сигнала
- Трансляционная инвариантность к небольшим неоднородностям в положении шаблонов во входном сигнале. Путем расчета агрегационных статистик небольших окрестностей входного сигнала подвыборка может игнорировать небольшие пространственные перемещения в нем
Плотные слои
Сверточные слои и слои подвыборки служат одной цели — генерации признаков изображения. Завершающим шагом является классификация входного изображения на основе обнаруженных признаков. В CNN это делают плотные слои на вершине сети. Эта часть сети называется классификационной. Она может содержать несколько слоев поверх друг друга с полной связностью, но обычно заканчивается слоем класса softmax, активированным многопеременной логистической активационной функцией, в котором количество блоков равняется количеству классов. На выходе этого слоя находится распределение вероятностей по классам для входного объекта. Теперь изображение можно классифицировать, выбрав наиболее вероятный класс.
