Доброго времени суток.

Я заметил интерес публики к вопросу о квантовой телепортации в частности и к квантовой механике в общем. Этот пост является в меру упрощенным объяснением основ квантовой механики и телепортации с точки зрения квантовой информации. То есть рассказов о том, как телепортировать луч света в домашних условиях используя синюю изоленту и DVD-привод не будет.
Всех, кто разбирается к квантовых протоколах связи — прошу в комментарии для обсуждения проблем и их решений.
Для начала давайте введем основные понятия:
Чтобы лучше понять, что это и как это работает, давайте для примера возмём простейшую квантовую систему, состоящую из одного фотона со спином вверх:
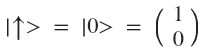
Это вполне себе такой обычный фотон, который можно произвести в любой лаборатории. Заметьте, что я записал вектор состояния фотона со спином вверх как вектор кубита 0 в базе
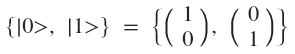 : спин фотона будет являться кубитом (квантовым битом информации) в нашем путешествии по квантовому миру.
: спин фотона будет являться кубитом (квантовым битом информации) в нашем путешествии по квантовому миру.
Теперь давайте введём эту систему в состояние суперпозиции с помощью преобразования Адамара:
Далее, давайте померяем спин нашего фотона. Как было сказано ранее, измерение будет проводиться в базе
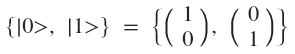 :
:
Это и есть состояние квантовой суперпозиции: до измерения, система находится в нескольких состояниях базы одновременно (т.е. вектор состояния системы равен сумме векторов базы с различными коэффициентами), а во время измерения «схлопывается» в одно из состояний базы с какой-то вероятностью. Никакой магии, просто числа.
Теперь давайте посмотрим, что такое квантовая запутанность. Для этого нам потребуется ввести понятие тензорного произведения:
Два запутанных фотона образуют систему, состояние которой можно выразить, например, следующим образом:
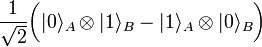
Я не буду объяснять, какая система называется запутанной (выйдет очень долго и не очень понятно), про это можно прочитать на Википедии. Вместо этого, давайте посмотрим, чем примечательна такая система.
Допустим, я хочу посмотреть вероятность нахождения этой системы в состоянии
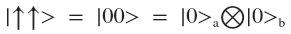
то есть когда два фотона имеют спин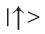 :
:
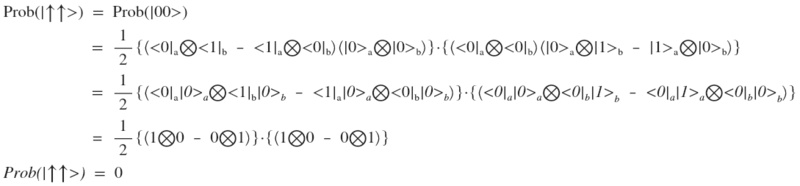
Аналогичный результат получается при расчете вероятности получения двух запутанных фотон в состоянии . Однако, если расчитать вероятность получения фотона а в состоянии
. Однако, если расчитать вероятность получения фотона а в состоянии 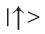 и фотона b в состоянии
и фотона b в состоянии  (то есть общее состояние системы
(то есть общее состояние системы 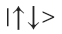 ) мы получим вероятность 1/2.
) мы получим вероятность 1/2.
Что это значит? А значит это, что имея систему из двух запутанных фотонов, померяв состояние одного из них, мы точно знаем состояние второго, на каком бы расстоянии друг от друга они не находились.
Посмотрев на основы квантовой механики, мы можем перейти к квантовой телепортации.
Поприветствуйте наших старых знакомых, Алису и Боба.
Итак, Алиса и Боб имеют синхронизированные часы и пару запутанных фотонов: один у Алисы, другой у Боба. Алиса измеряет состояние её фотона, и получает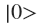 (с вероятностью 0.5, как мы видели ранее). В этот же момент времени фотон Боба принимает состояние
(с вероятностью 0.5, как мы видели ранее). В этот же момент времени фотон Боба принимает состояние 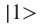 . Через время T (дабы не опередить Алису) Боб проводит измерения над своим фотоном, и понимает, какой результат измерения получила Алиса.
. Через время T (дабы не опередить Алису) Боб проводит измерения над своим фотоном, и понимает, какой результат измерения получила Алиса.

Проблема здесь очень простая и очевидная: Алиса не может контролировать состояние её фотона после измерения.
Предположим, Алиса хочет передать Бобу следующую последовательность бит: «011001». Для этого им с Бобом потребуются 6 пар запутанных фотонов. Алиса производит измерения всех шести, и получает следующий результат: «010111». Соответственно Боб получает «101000», применят операцию XOR дабы получить последовательность, которая была получена у Алисы: «010111». Однако Боб не знает, какую именно последовательность Алиса хотела передать. Для того, что бы полностью востановить переданное сообщение на стороне Боба, Алиса должна послать ему по классическому каналу информацию о полученных ей ошибках: «001110». Получив эту информацию, Боб может без труда восстановить сообщение Алисы: «011001».
Как мы видим, использование квантового классического канала при передачи данных, неизбежно. В чем плюсы такой передачи, спросите вы? При квантовой передаче исключается возможность атаки «Man in the middle»: даже если информация об ошибках будет перехвачена, она не поможет злоумышленнику узнать передаваемое сообщение. Единственное, что может сделать злоумышленник, так это изменить информацию об ошибках, но от этого тоже есть защита, использующая квантовые свойства.
Но об этом уже в другой раз.

Я заметил интерес публики к вопросу о квантовой телепортации в частности и к квантовой механике в общем. Этот пост является в меру упрощенным объяснением основ квантовой механики и телепортации с точки зрения квантовой информации. То есть рассказов о том, как телепортировать луч света в домашних условиях используя синюю изоленту и DVD-привод не будет.
Всех, кто разбирается к квантовых протоколах связи — прошу в комментарии для обсуждения проблем и их решений.
Основы квантовой механики
Для начала давайте введем основные понятия:
- Состояние системы в квантовой механике представляется вектором. Запись ведётся обозначениями Дирака.
- Состояния системы после измерения (то есть состояние, которое мы видим извне) представляют собой ортонормальную базу. Другими словами, измерения происходят в ортонормальной базе состояний.
- Измерение есть ни что иное как проекция вектора состояния системы на один из векторов измерительной базы:
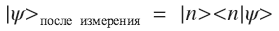
- Вероятность того, что система
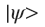 будет проецирована на вектор
будет проецирована на вектор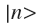 :
:

Чтобы лучше понять, что это и как это работает, давайте для примера возмём простейшую квантовую систему, состоящую из одного фотона со спином вверх:
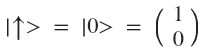
Это вполне себе такой обычный фотон, который можно произвести в любой лаборатории. Заметьте, что я записал вектор состояния фотона со спином вверх как вектор кубита 0 в базе
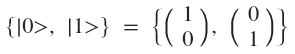 : спин фотона будет являться кубитом (квантовым битом информации) в нашем путешествии по квантовому миру.
: спин фотона будет являться кубитом (квантовым битом информации) в нашем путешествии по квантовому миру.Теперь давайте введём эту систему в состояние суперпозиции с помощью преобразования Адамара:
- Матрица преобразования:

- Состояние системы после преобразования:

Далее, давайте померяем спин нашего фотона. Как было сказано ранее, измерение будет проводиться в базе
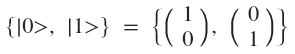 :
:- Вероятность получить
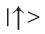 :
:
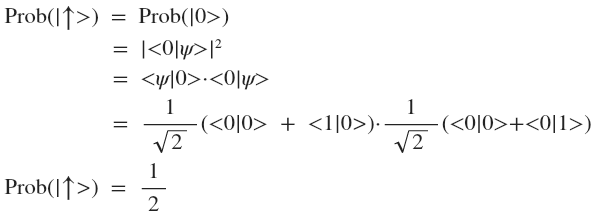
- Вероятность получить
 :
:
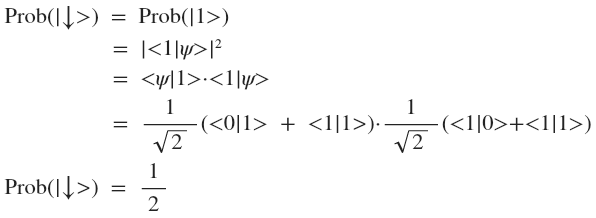
Это и есть состояние квантовой суперпозиции: до измерения, система находится в нескольких состояниях базы одновременно (т.е. вектор состояния системы равен сумме векторов базы с различными коэффициентами), а во время измерения «схлопывается» в одно из состояний базы с какой-то вероятностью. Никакой магии, просто числа.
Теперь давайте посмотрим, что такое квантовая запутанность. Для этого нам потребуется ввести понятие тензорного произведения:
Тензорное произведение состояний двух фотонов
Возмём два фотона, состояния которых опишем двумя Гилбертовыми пространствами 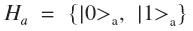 и
и 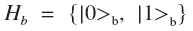 . Тензорным произведением этих пространств будет
. Тензорным произведением этих пространств будет
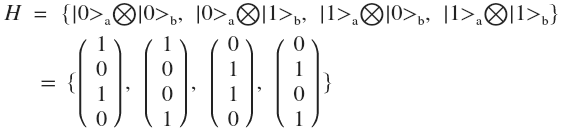
В этом же пространстве будет описана система, состоящая из двух фонов, один из которых принадлежит пространству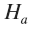 , а второй —
, а второй — 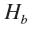 .
.
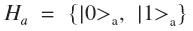 и
и 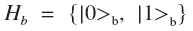 . Тензорным произведением этих пространств будет
. Тензорным произведением этих пространств будет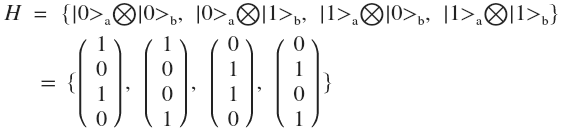
В этом же пространстве будет описана система, состоящая из двух фонов, один из которых принадлежит пространству
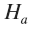 , а второй —
, а второй — 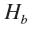 .
.Два запутанных фотона образуют систему, состояние которой можно выразить, например, следующим образом:
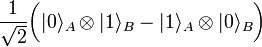
Я не буду объяснять, какая система называется запутанной (выйдет очень долго и не очень понятно), про это можно прочитать на Википедии. Вместо этого, давайте посмотрим, чем примечательна такая система.
Допустим, я хочу посмотреть вероятность нахождения этой системы в состоянии
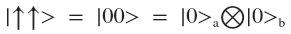
то есть когда два фотона имеют спин
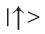 :
: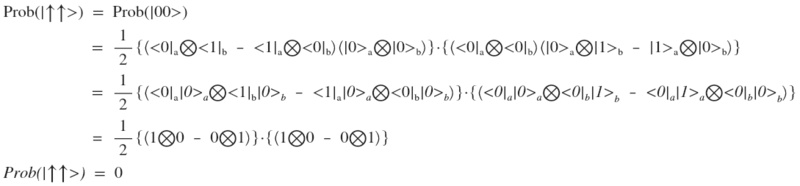
Аналогичный результат получается при расчете вероятности получения двух запутанных фотон в состоянии
 . Однако, если расчитать вероятность получения фотона а в состоянии
. Однако, если расчитать вероятность получения фотона а в состоянии 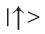 и фотона b в состоянии
и фотона b в состоянии  (то есть общее состояние системы
(то есть общее состояние системы 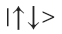 ) мы получим вероятность 1/2.
) мы получим вероятность 1/2.Что это значит? А значит это, что имея систему из двух запутанных фотонов, померяв состояние одного из них, мы точно знаем состояние второго, на каком бы расстоянии друг от друга они не находились.
Посмотрев на основы квантовой механики, мы можем перейти к квантовой телепортации.
Квантовая телепортация
Поприветствуйте наших старых знакомых, Алису и Боба.

Итак, Алиса и Боб имеют синхронизированные часы и пару запутанных фотонов: один у Алисы, другой у Боба. Алиса измеряет состояние её фотона, и получает
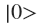 (с вероятностью 0.5, как мы видели ранее). В этот же момент времени фотон Боба принимает состояние
(с вероятностью 0.5, как мы видели ранее). В этот же момент времени фотон Боба принимает состояние 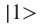 . Через время T (дабы не опередить Алису) Боб проводит измерения над своим фотоном, и понимает, какой результат измерения получила Алиса.
. Через время T (дабы не опередить Алису) Боб проводит измерения над своим фотоном, и понимает, какой результат измерения получила Алиса.
Проблема здесь очень простая и очевидная: Алиса не может контролировать состояние её фотона после измерения.
Предположим, Алиса хочет передать Бобу следующую последовательность бит: «011001». Для этого им с Бобом потребуются 6 пар запутанных фотонов. Алиса производит измерения всех шести, и получает следующий результат: «010111». Соответственно Боб получает «101000», применят операцию XOR дабы получить последовательность, которая была получена у Алисы: «010111». Однако Боб не знает, какую именно последовательность Алиса хотела передать. Для того, что бы полностью востановить переданное сообщение на стороне Боба, Алиса должна послать ему по классическому каналу информацию о полученных ей ошибках: «001110». Получив эту информацию, Боб может без труда восстановить сообщение Алисы: «011001».
Как мы видим, использование квантового классического канала при передачи данных, неизбежно. В чем плюсы такой передачи, спросите вы? При квантовой передаче исключается возможность атаки «Man in the middle»: даже если информация об ошибках будет перехвачена, она не поможет злоумышленнику узнать передаваемое сообщение. Единственное, что может сделать злоумышленник, так это изменить информацию об ошибках, но от этого тоже есть защита, использующая квантовые свойства.
Но об этом уже в другой раз.