Comments 188
Чего только не бывает на хабре в пятницу вечером.
+28
Прочитал много нового и интересного для себя, но… Почему, черт побери, фраза «Простыми словами» в заголовке всегда означает «мы старательно замолчим все определения и выводы формул, чтобы вам все равно пришлось после нашей статьи читать что-нибудь еще на ту же тему, да еще и будем перескакивать с пятого на десятое в процессе изложения»?
+14
Просто текст и так вышел очень длинный, а мне хотелось что бы его все-таки дочитали до конца, не застряв в куче формул в начале. Тем более что основные формулы я все же привел, опустив только широко известные определения. Основные идеи по выводу формул там тоже вроде все есть, а «честные» их доказательства — это очень хардкорный матан, так как там оперирование идет обобщенными функциями. Но если у Вас есть какие-то идеи что конкретно можно добавить в статью — то я их с благодарностью выслушаю и текст соответствующим образом подправлю.
+7
Я понимаю вашу точку зрения, но позиция mayorovp в данном случае больше соответствует моему личному мнению на тему, как такие вещи объяснять.
Основная проблема ситуации, когда часть необходимых для понимания главной идеи статьи вещей вынесена во внешние ссылки — в том, что материал по этим внешним ссылкам имеет иной, часто более общий посыл, чем та статья, за которую берётся читатель. Я учился на профильном факультете по профильной специальности, и на слух термины типа «свёртка» мне знакомы. Тем не менее, я просто уверен, что пойдя в Википедию за точным определением, я зависну там ещё на несколько часов, потому что эта пресловутая свёртка будет выражаться через какие-то другие давно забытые мной вещи, а те — через ещё что-то. В итоге ситуация будет похожа на попытку скомпилить у себя в голове целую библиотеку математических понятий, из которой мне на самом деле нужна лишь маленькая часть, но пока я не завершу эту компиляцию, я не пойму, какая именно. Это сложный, утомительный, трудоёмкий и фрустрирующий процесс для человека, который повёлся на «простыми словами».
Сейчас ваша работа мало чем отличается от множества просветительских статей на аналогичную тематику. И все они грешат одним и тем же: опуская базисные вещи, оставляя их на совести читателя, они в итоге этого самого читателя и лишаются, ибо до конца в таком «простом» мануале смогут дойти лишь те, кто и так разбирался в материале, либо те у кого было реально много времени и желания разбираться.
Не мне вам вменять что-либо в вину, ибо критиковать всегда проще, чем делать. Но я бы с гораздо большим удовольствием прочёл целый цикл статей на тему преобразования Фурье, где вся необходимая математика тоже была бы включена в комплект поставки. Да, это запарнее делать, но зато любой, обладающий действительно общераспространёнными базовыми знаниями (на уровне дифференциального и интегрального исчислений хотя бы) будет уверен, что по прочтении всего цикла он будет действительно понимать поданный материал. А вы создадите действительно ценный мануал по конкретной теме, а в качестве приятного бонуса отхватите плюсов за каждую из его частей, опубликованную отдельным постом =).
PS: Если вы были бы готовы взяться за такой титанический труд, я мог бы вам посодействовать в качестве подопытного читателя, на котором можно было бы тестировать понятность и доходчивость материала.
Основная проблема ситуации, когда часть необходимых для понимания главной идеи статьи вещей вынесена во внешние ссылки — в том, что материал по этим внешним ссылкам имеет иной, часто более общий посыл, чем та статья, за которую берётся читатель. Я учился на профильном факультете по профильной специальности, и на слух термины типа «свёртка» мне знакомы. Тем не менее, я просто уверен, что пойдя в Википедию за точным определением, я зависну там ещё на несколько часов, потому что эта пресловутая свёртка будет выражаться через какие-то другие давно забытые мной вещи, а те — через ещё что-то. В итоге ситуация будет похожа на попытку скомпилить у себя в голове целую библиотеку математических понятий, из которой мне на самом деле нужна лишь маленькая часть, но пока я не завершу эту компиляцию, я не пойму, какая именно. Это сложный, утомительный, трудоёмкий и фрустрирующий процесс для человека, который повёлся на «простыми словами».
Сейчас ваша работа мало чем отличается от множества просветительских статей на аналогичную тематику. И все они грешат одним и тем же: опуская базисные вещи, оставляя их на совести читателя, они в итоге этого самого читателя и лишаются, ибо до конца в таком «простом» мануале смогут дойти лишь те, кто и так разбирался в материале, либо те у кого было реально много времени и желания разбираться.
Не мне вам вменять что-либо в вину, ибо критиковать всегда проще, чем делать. Но я бы с гораздо большим удовольствием прочёл целый цикл статей на тему преобразования Фурье, где вся необходимая математика тоже была бы включена в комплект поставки. Да, это запарнее делать, но зато любой, обладающий действительно общераспространёнными базовыми знаниями (на уровне дифференциального и интегрального исчислений хотя бы) будет уверен, что по прочтении всего цикла он будет действительно понимать поданный материал. А вы создадите действительно ценный мануал по конкретной теме, а в качестве приятного бонуса отхватите плюсов за каждую из его частей, опубликованную отдельным постом =).
PS: Если вы были бы готовы взяться за такой титанический труд, я мог бы вам посодействовать в качестве подопытного читателя, на котором можно было бы тестировать понятность и доходчивость материала.
+13
Я попробую дописать еще одну-две статьи на смежные темы. Правильно ли я понял, что основные затруднения были связаны со сверткой и дельта-функцией Дирака? Я напишу тогда одну небольшую статью про эту замечательную парочку и еще одну статью о том, как их используют при интерполяции и фильтрации сигналов и изображений
+3
Если эти темы будут так же проработаны, обязательно пишите.
Эта статья не для новичков, а для тех, кто использовал уже FT, но не знал многих интересных свойств.
Например, только недавно я обдумывал, почему на маленьком окне выше погрешность обнаружения частот. Интуитивно понятно — меньше информации, но здесь всё досконально расписано.
Эта статья не для новичков, а для тех, кто использовал уже FT, но не знал многих интересных свойств.
Например, только недавно я обдумывал, почему на маленьком окне выше погрешность обнаружения частот. Интуитивно понятно — меньше информации, но здесь всё досконально расписано.
0
Видите ли, я взялся за вашу статью вечером в пятницу в очень расслабленном состоянии. Потому что «простыми словами», а тема вроде как интересная. В итоге я споткнулся о первую же внешнюю отсылку к вещам, которые на моей памяти уже не ассоциировались с чем-то простым. А дальше просто не читал. Поэтому описанный сценарий с потерянным читателем — ровно про меня.
Так что у меня нет запросов на расшифровку какого-то конкретного понятия. У меня был запрос скорее на целостность подачи материала, позволяющую получить все необходимые знания в одном месте и от одного автора. Последнее очень важно, потому что тот же энциклопедический стиль подачи материала в Википедии настолько сух, что использовать её как учебник, а не как справочник, в большинстве случаев очень неудобно. А сторонний автор не ограничен теми гайдлайнами, которые обязательны для Википедии, и может подать материал менее формально, но зато куда более доходчиво.
Раз уж вы поинтересовались моим мнением, то я постарался всё-таки просмотреть статью по диагонали и высказать более конструктивные замечания.
Первое что можно отметить — это очень высокая концентрация терминов и постоянные отсылки к ним в процессе объяснения. Некоторые термины вводятся прямо по ходу дела, после чего постоянно используются.
Здесь вы допускаете типичную ошибку лектора технического вуза: большинство студентов не успевают с ходу понимать и запоминать все вводимые понятия, после чего в какой-то момент повествования они теряют главную нить и начинают тупо конспектировать с мыслью «как-нибудь дома разберусь».
В вашем случае, так как речь всё же не идёт о лекции в реальном времени, помог бы отдельный глоссарий всех использованных терминов и выделение оных в тексте, как стилистически, так и с помощью гиперссылок, ведущих на соответствующий пункт глоссария. Это радикально облегчит неторопливому читателю проблему понимания нового для себя материала и даст ему уверенность в том, что автор не оставит его наедине с какими-то мудрёными логическими переходами.
Второе. Эти самые логические переходы.
На мой вкус, у вас очень action-packed манера изложения. Минимум воды и разжёвывания, максимум стремительности и выведения одних вещей из других. Это круто для блокбастеров, но для статей на научную тематику чуть более дружественный к читателю-новичку стиль был бы приятнее. Как у Фленагана в JavaScript Definitive Guide: он нередко повторяет вкратце уже ранее данные полновесные объяснения, чтобы напомнить читателю какие-то вещи, о которых он читал 50 страниц назад, без необходимости мотаться по книге в поисках нужной страницы. Плюс, дотошно объясняя порой кажущиеся простыми вещи, иногда по несколько раз, но с чуть разных точек зрения, он даёт всестороннее представление о той или иной вещи, не оставляя шанса для некорректного или однобокого понимания, которое может возникнуть при более кратком пояснении.
Я понимаю, что вас смущал объём текста. С необходимой водой, которой он был бы разбавлен до состояния, действительно доступного новичкам в пятницу вечером, текста стало бы в три раза больше. Но, как я уже писал в первом комментарии, тему можно было бы разбить на несколько тематических постов, и тогда проблема объёма не стояла бы так остро.
В общем, отзыв я вам предоставил, что теперь делать — решать вам. Обладай я вашими техническими знаниями и кучей свободного времени, я бы писал не дополнительные статьи на смежные темы, а создал бы этот цикл заново, а данную тему оставил в назидание потомкам как иллюстрацию того, что просто о сложном говорить всё-таки непросто =).
Если хотите, я мог бы помочь вам с редактурой. Плюс, я такой тугодум, что если я всё пойму — значит поймёт практически любой читатель =).
Так что у меня нет запросов на расшифровку какого-то конкретного понятия. У меня был запрос скорее на целостность подачи материала, позволяющую получить все необходимые знания в одном месте и от одного автора. Последнее очень важно, потому что тот же энциклопедический стиль подачи материала в Википедии настолько сух, что использовать её как учебник, а не как справочник, в большинстве случаев очень неудобно. А сторонний автор не ограничен теми гайдлайнами, которые обязательны для Википедии, и может подать материал менее формально, но зато куда более доходчиво.
Раз уж вы поинтересовались моим мнением, то я постарался всё-таки просмотреть статью по диагонали и высказать более конструктивные замечания.
Первое что можно отметить — это очень высокая концентрация терминов и постоянные отсылки к ним в процессе объяснения. Некоторые термины вводятся прямо по ходу дела, после чего постоянно используются.
Здесь вы допускаете типичную ошибку лектора технического вуза: большинство студентов не успевают с ходу понимать и запоминать все вводимые понятия, после чего в какой-то момент повествования они теряют главную нить и начинают тупо конспектировать с мыслью «как-нибудь дома разберусь».
В вашем случае, так как речь всё же не идёт о лекции в реальном времени, помог бы отдельный глоссарий всех использованных терминов и выделение оных в тексте, как стилистически, так и с помощью гиперссылок, ведущих на соответствующий пункт глоссария. Это радикально облегчит неторопливому читателю проблему понимания нового для себя материала и даст ему уверенность в том, что автор не оставит его наедине с какими-то мудрёными логическими переходами.
Второе. Эти самые логические переходы.
На мой вкус, у вас очень action-packed манера изложения. Минимум воды и разжёвывания, максимум стремительности и выведения одних вещей из других. Это круто для блокбастеров, но для статей на научную тематику чуть более дружественный к читателю-новичку стиль был бы приятнее. Как у Фленагана в JavaScript Definitive Guide: он нередко повторяет вкратце уже ранее данные полновесные объяснения, чтобы напомнить читателю какие-то вещи, о которых он читал 50 страниц назад, без необходимости мотаться по книге в поисках нужной страницы. Плюс, дотошно объясняя порой кажущиеся простыми вещи, иногда по несколько раз, но с чуть разных точек зрения, он даёт всестороннее представление о той или иной вещи, не оставляя шанса для некорректного или однобокого понимания, которое может возникнуть при более кратком пояснении.
Я понимаю, что вас смущал объём текста. С необходимой водой, которой он был бы разбавлен до состояния, действительно доступного новичкам в пятницу вечером, текста стало бы в три раза больше. Но, как я уже писал в первом комментарии, тему можно было бы разбить на несколько тематических постов, и тогда проблема объёма не стояла бы так остро.
В общем, отзыв я вам предоставил, что теперь делать — решать вам. Обладай я вашими техническими знаниями и кучей свободного времени, я бы писал не дополнительные статьи на смежные темы, а создал бы этот цикл заново, а данную тему оставил в назидание потомкам как иллюстрацию того, что просто о сложном говорить всё-таки непросто =).
Если хотите, я мог бы помочь вам с редактурой. Плюс, я такой тугодум, что если я всё пойму — значит поймёт практически любой читатель =).
+1
Кому как. Меня бы это разжёвывание свёртки только бы заставило искать, где оно заканчивается и начинается суть.
0
Меня в американских книжках убивает такая вода с миллионами повторов. В каждом из них встречается очередной важный аспект, не упомянутый ранее, типа чтобы не грузить, и из-за этого, а ещё и из-за того, что эти повторы никак не отделены от повествования, их не получается пропускать. Чувствую себя курицей, выклёвывающей вкусные зернышки из залежей навоза.
+1
Я где-то встречал на Хабре комментарий про сравнение манеры подачи материала у нас и на Западе: там грешат излишней популяризацией, а у нас — излишней сухостью.
Тот минус, который вы описали, можно исключить, если в одном месте будет находиться самое полное определение термина, а при его использовании будут даваться либо гиперссылки, либо спрятанными в спойлер-блоки цитаты. Причём цитировать можно уже именно тот фрагмент, который максимально актуален для конкретного контекста, в котором термин был использован.
Грамотная вода может сильно облегчить понимание. При этом претензии тех, кому она без надобности, вполне удовлетворяются соответствующим стилистическим оформлением текста. Однако домыслить эту воду, если текст изначально создавался в сухом и лаконичном стиле, намного сложнее. А уж если американские книжки так грешат этой популяризацией, что это стало притчей во языцех, значит таки бывает от неё польза, и совсем списывать со счетов дружественную к новичку манеру подачи не стоит.
Тот минус, который вы описали, можно исключить, если в одном месте будет находиться самое полное определение термина, а при его использовании будут даваться либо гиперссылки, либо спрятанными в спойлер-блоки цитаты. Причём цитировать можно уже именно тот фрагмент, который максимально актуален для конкретного контекста, в котором термин был использован.
Грамотная вода может сильно облегчить понимание. При этом претензии тех, кому она без надобности, вполне удовлетворяются соответствующим стилистическим оформлением текста. Однако домыслить эту воду, если текст изначально создавался в сухом и лаконичном стиле, намного сложнее. А уж если американские книжки так грешат этой популяризацией, что это стало притчей во языцех, значит таки бывает от неё польза, и совсем списывать со счетов дружественную к новичку манеру подачи не стоит.
0
Беда в том, что почти никто выделением и оформлением повторов не заморачивается…
Авторы, злоупотребляющие повторами, мне кажется, даже отчёта себе не отдают, что повтор очередной лепят.
Авторы, злоупотребляющие повторами, мне кажется, даже отчёта себе не отдают, что повтор очередной лепят.
0
Ну что уж поделать, мир не совершенен =).
Всех авторов не изменишь, да. А вот попробовать уломать конкретно автора этой статьи на использование гибридного стиля для последующих постов — вполне реально. Если получится — можно будет даже собственными глазами наблюдать разницу и думать, получилось ли достичь желаемого результата.
Всех авторов не изменишь, да. А вот попробовать уломать конкретно автора этой статьи на использование гибридного стиля для последующих постов — вполне реально. Если получится — можно будет даже собственными глазами наблюдать разницу и думать, получилось ли достичь желаемого результата.
+1
Для меня большим открытием оказалось применение Фурье для дискретизации аналогового сигнала. Респект.
Однако, как-то не хватило подробностей про чаще встречающееся разложение сигнала на гармоники. Везде вижу, но ни разу не понял, как это — произвольную функцию представить суммой синусоид?..
Однако, как-то не хватило подробностей про чаще встречающееся разложение сигнала на гармоники. Везде вижу, но ни разу не понял, как это — произвольную функцию представить суммой синусоид?..
0
> Для меня большим открытием оказалось применение Фурье для дискретизации аналогового сигнала.
Стесняюсь спросить. Для чего, как Вы думали раньше, преобразование Фурье применяется чаще?
Стесняюсь спросить. Для чего, как Вы думали раньше, преобразование Фурье применяется чаще?
0
А произвольную функцию и нельзя представить суммой синусоид. Довольно часто непрерывное преобразование Фурье пытаются интерпретировать именно подобным образом, но эта интерпретация неверна.
Вот периодический сигнал разложить в сумму синусоид можно. Дискретный сигнал (последовательность чисел) тоже в определенном смысле можно.
Вот периодический сигнал разложить в сумму синусоид можно. Дискретный сигнал (последовательность чисел) тоже в определенном смысле можно.
+1
Слышал вариант «нужный кусок области определения функции растиражировать вдоль оси — и можно считать её периодической»…
0
А теперь до меня, кажется, начинает доходить, что наверно в результате такого разложения получится лишь спектр, то есть усреднённая оценка наличия в раскладываемом сигнале следов разных частот. Спектрограммы так рисуют, наверное, порезав сигнал на кусочки и разложив каждый отдельно, да? Восстановить, я так понимаю, сигнал в исходном виде — почти невозможно, лишь равномерную смесь синусоид. Да?
0
Ну, в общем, да, непрерывный спектр — это в приближенном смысле усредненная оценка наличия в раскладываемом сигнале следов разных частот. Просто проблематично определить что такое «наличие в сигнале частоты x». На практике делают ровно наоборот — определяют понятие «спектральной плотности» и вообще «частоты в спектре сигнала» через преобразование Фурье, которое определяют через формулы.
Спектрограммы действительно рисуют, порезав сигнал на кусочки и разлагая каждый кусочек отдельно (полагая функцию вне взятого кусочка равной нулю). При этом, как я писал выше, происходит «спектральная утечка» — чем «тоньше» нарезка, тем сильнее спектр, скажем, синусоиды, расплывается по частотам. Из-за этой утечки точно восстановить исходный сигнал по конечному отрезку этого сигнала без дополнительной информации невозможно (хотя приближенно, с довольно хорошей точностью, — можно).
Спектрограммы действительно рисуют, порезав сигнал на кусочки и разлагая каждый кусочек отдельно (полагая функцию вне взятого кусочка равной нулю). При этом, как я писал выше, происходит «спектральная утечка» — чем «тоньше» нарезка, тем сильнее спектр, скажем, синусоиды, расплывается по частотам. Из-за этой утечки точно восстановить исходный сигнал по конечному отрезку этого сигнала без дополнительной информации невозможно (хотя приближенно, с довольно хорошей точностью, — можно).
+1
Спасибо!
То есть получается, что принято говорить о наличии частоты X в спектре — когда преобразование Фурье выдаёт для неё какую-либо амплитуду, да?
А если колебания с такой частотой присутствуют на половине продолжительности сигнала, амплитуда этой частоты в получаемом результате преобразования будет вдвое меньше, чем если эти колебания присутствуют всё время сигнала?
Ещё соображения возникли: кроме как через Фурье, наличие частоты в звуковом сигнале можно приблизительно определять органами чувств — на слух. Ну, и на глаз — по внешнему виду кривой сигнала.
На слух мы определяем наличие какой-то частоты в звуке по реакции слуховых ресничек в улитке внутреннего уха. Типа, смог сигнал раскачать ресничку на участке соответствующего диаметра — значит, есть такая частота. Продолжает качать долго — значит, она длится. Не успел раскачать и закончился — нет частоты. Не смог раскачать потому что слаб — нет частоты. В преобразовании Фурье есть аналогии этим процессам? Подобные пороги чувствительности по амплитуде и продолжительности там как-нибудь отражаются?
То есть получается, что принято говорить о наличии частоты X в спектре — когда преобразование Фурье выдаёт для неё какую-либо амплитуду, да?
А если колебания с такой частотой присутствуют на половине продолжительности сигнала, амплитуда этой частоты в получаемом результате преобразования будет вдвое меньше, чем если эти колебания присутствуют всё время сигнала?
Ещё соображения возникли: кроме как через Фурье, наличие частоты в звуковом сигнале можно приблизительно определять органами чувств — на слух. Ну, и на глаз — по внешнему виду кривой сигнала.
На слух мы определяем наличие какой-то частоты в звуке по реакции слуховых ресничек в улитке внутреннего уха. Типа, смог сигнал раскачать ресничку на участке соответствующего диаметра — значит, есть такая частота. Продолжает качать долго — значит, она длится. Не успел раскачать и закончился — нет частоты. Не смог раскачать потому что слаб — нет частоты. В преобразовании Фурье есть аналогии этим процессам? Подобные пороги чувствительности по амплитуде и продолжительности там как-нибудь отражаются?
0
Да, с определением частоты все именно так.
С амплитудой колебаний присутствующих лишь в половине сигнала — в первом приближении да. Однако там еще будет «размытие» колебания по соседним частотам.
«Кроме Фурье» колебания можно определять через частотные фильтры. Представим себе фильтр, который синусоидальный сигнал определенной частоты пропускает, а все остальные сигналы — подавляет. Тогда наличие в сигнале данной частоты можно определить по наличию синусоиды на выходе подобного фильтра при подаче на него сигнала.
«На слух» и «на глаз» частоты все же лучше не определять. Например, есть такой эффект как «звуковые биения» — это когда в сигнале есть две близкие частоты и за счет их интерференции субъективная громкость сигнала периодически меняется. На слух человек хорошо слышит эти биения и воспринимает их как звук низкой частоты, да и в графике сигнала их хорошо видно, тогда как в исходном сигнале этой частоты нет.
А физиология слуха — это вообще очень интересная и сложная тема, но я так понимаю, точного механизма там никто не знает. Там есть аналогии с Фурье, есть с вейвлетами, а единой модели нет.
С амплитудой колебаний присутствующих лишь в половине сигнала — в первом приближении да. Однако там еще будет «размытие» колебания по соседним частотам.
«Кроме Фурье» колебания можно определять через частотные фильтры. Представим себе фильтр, который синусоидальный сигнал определенной частоты пропускает, а все остальные сигналы — подавляет. Тогда наличие в сигнале данной частоты можно определить по наличию синусоиды на выходе подобного фильтра при подаче на него сигнала.
«На слух» и «на глаз» частоты все же лучше не определять. Например, есть такой эффект как «звуковые биения» — это когда в сигнале есть две близкие частоты и за счет их интерференции субъективная громкость сигнала периодически меняется. На слух человек хорошо слышит эти биения и воспринимает их как звук низкой частоты, да и в графике сигнала их хорошо видно, тогда как в исходном сигнале этой частоты нет.
А физиология слуха — это вообще очень интересная и сложная тема, но я так понимаю, точного механизма там никто не знает. Там есть аналогии с Фурье, есть с вейвлетами, а единой модели нет.
+1
Вы же сами понимаете, что главные трудности здесь возникают со свёрткой и дельта-функцией.
Дельта-функцию из википедии ещё можно понять (хоть и знал это раньше), а со свёрткой совсем беда. В вики про свёртку написано, что это «операция, показывающая схожесть двух функций». И дальше интеграл по какому-то Rd. Кто все эти функции, и чего они от меня хотят?
Хотелось бы определение таких базовых вещей в простом виде.
> habrastorage.org/storage3/7fd/edc/db5/7fdedcdb526b3b711c192d5902351969.png
А здесь почему отрезки вверх кончаются стрелочками?
Дельта-функцию из википедии ещё можно понять (хоть и знал это раньше), а со свёрткой совсем беда. В вики про свёртку написано, что это «операция, показывающая схожесть двух функций». И дальше интеграл по какому-то Rd. Кто все эти функции, и чего они от меня хотят?
Хотелось бы определение таких базовых вещей в простом виде.
> habrastorage.org/storage3/7fd/edc/db5/7fdedcdb526b3b711c192d5902351969.png
А здесь почему отрезки вверх кончаются стрелочками?
+1
А здесь почему отрезки вверх кончаются стрелочками?Потому что это — условная бесконечность, умноженная на коэффициент. Строго говоря, значение в такой точке не определено, но при этом (за счет «магии» обобщенных функций) такие значения можно сравнивать друг с другом, и даже можно выполнять над ними арифметические действия. Отсюда и стрелочка — чтобы можно было отобразить это на графике, и при этом не перепутать с регулярной точкой.
0
Аналогично, я половину операций просто не помню как делать, поэтому выражения — легко представить и простое преобразование становятся непонятными и в этот момент теряешь нить. Причем нужны отнюдь не формулы — их я найду без проблем, мне нужно объяснение на пальцах пошагово, как это делается и самое главное — примеры из жизни для каждого момента — если делаем свертку, то как на википедии изображена картинка, которая легко дает понять почему свертка — есть особый вид интегрирования. Нужны простые и понятны примеры, которые непроходимые уродские формулы сделают понятными и осязаемыми. Без физического смысла математика — полная абстракция и совершенно неинетересна.
Нужно показывать применение — если выполняем преобразование, то что оно дает. Зачем мы занимаемся скучной работой и нудным головоломным интегрированием.
Нужно показывать применение — если выполняем преобразование, то что оно дает. Зачем мы занимаемся скучной работой и нудным головоломным интегрированием.
+2
Очень разумные и правильные замечания. По своему опыту могу подтвердить, что без завершения «компиляции библиотеки математических понятий» та самая нужная «маленькая часть» так и не будет понята до конца.
+2
и поскольку часто не удается выделить столько времени, чтобы уложить в голове по полочкам все, что нужно, то окончательного понимания так и не приходит. Имеем образование по верхушкам. Обсудить можем- применить не всегда.
+2
Пока не припрет необходимость. Обсуждение — это ведь не работа, а понимание приходит только когда плотно работаешь с такими вещами
0
А у меня в работе вообще нет необходимости в высшей математике. Я ее применяю только в хобби. Сейчас вот понадобилась для обработки данных с сенсоров и построения алгоритма полетного контроллера. В целом же для меня математика — это способ снизить алгоритмическую сложность программы. Это инструмент для обработки данных, которые — самое ценное, что есть в моей практике.
0
Тогда лучше заменить заголовок на «своими словами»
+1
Не слушайте недовольных, обзор у Вас получился отличный. Народ просто не понимает смысл научных обзоров, задача которых — создать в голове читателя общее представление о той области, изучить которую человеку еще только предстоит. Даже если часть доказательств остается пока непонятной, наличие такой общей картины способно во много раз сократить затраты времени на полноценное изучение. А для людей, которые уже изучили этот материал, такой обзор поможет структурировать материал в голове, разложить все по полочкам. Так что читать его лучше дважды — до и после.
В целом изложенный Вами материал примерно соответствует тому, что у меня в курсе ЦОС студенты изучают в течение целого семестра, так что плотность материала идеальная для обзора и все претензии по поводу отсутствия доказательств совершенно не по делу.
В целом изложенный Вами материал примерно соответствует тому, что у меня в курсе ЦОС студенты изучают в течение целого семестра, так что плотность материала идеальная для обзора и все претензии по поводу отсутствия доказательств совершенно не по делу.
0
Спасибо большое, очень приятно было прочитать этот комментарий!
Материал я думаю было бы все же неплохо дополнить рассказом про свертки и фильтры, тогда он был бы полным и давал более завершенную картину. И благодаря Вам этот рассказ стал немножко ближе к его практическому воплощению :)
Материал я думаю было бы все же неплохо дополнить рассказом про свертки и фильтры, тогда он был бы полным и давал более завершенную картину. И благодаря Вам этот рассказ стал немножко ближе к его практическому воплощению :)
0
Если там (в ЦФ и свертках) у Вас все так же хорошо продумано, как в спектрах, то получится просто замечательный и довольно полный обзор. На самом деле обзоры ведь хороши еще и тем, что в хорошем обзоре собраны в концентрированном виде объяснения смысла вводимых понятий — зачем они нужны и почему работают — те общие слова, которые математики часто пропускают, считая их слишком «физичными», и которые приходится по капле выискивать в разных книжках. В этой части у Вас с этим все очень хорошо.
Кстати, такое понимание предмета очень трудно достижимо просто по книжкам, без опыта практической работы в данной области. Так что я бы почти достоверно идентифицировал Вас как коллегу :)
Кстати, такое понимание предмета очень трудно достижимо просто по книжкам, без опыта практической работы в данной области. Так что я бы почти достоверно идентифицировал Вас как коллегу :)
0
Автор хотел более доходчиво донести «физику явления». А формулы и их выводы можно в книжках посмотреть. Мне, например, очень понравилась часть статьи, где объясняется, почему применение окон приводит к растеканию спектра.
+1
PS после исправления статьи автором она стала читаться гораздо лучше, так что прошу мой комментарий выше считать устаревшим.
0
Угу, причем то, что объясняется о полезности этих преобразований, я и так понял из статьи на Википедии и помню из университетского курса, а вот как именно проводить свертку функций, как именно восстанавливать сигнал и как это превратить в полезный алгоритм я так и не понял. Текст пестрит любимыми математическими выражениями «очевидно» и «легко сделать», а на деле эти опускаемые моменты и являются самыми сложными и непонятными. В итоге поверхностно я понимаю эту тему, а пользоваться так и не могу. «Просто» не получилось. Самое интересное опущено, а то, о чем можно догадаться и понять на пальцах я и так уже давно понял.
+2
Да… И это еще «простыми словами». В целом, строгое описание куда понятнее.
+7
Иллюстрации крутецки круты.
+11
Довольно хорошо написано и проиллюстрировано, хотя, раньше встречал еще более простое и изящное изложение преобразования Фурье, правда, сейчас уже не вспомню источник, кажется даже из курса каких-то лекций. Ключевым приемом таких публикаций является проведение аналогий и ассоциаций с предметами и событиями из повседневной жизни, что даже люди далекие от темы улавливают суть. Тот же Джоэль Спольски часто прибегает к такому подходу и другие известные популяризаторы, Джефф Хокинс вспомнился со своей книгой. Но в целом написано очень неплохо, с указанием ключевых моментов и подводных камней!
А могли бы вы столь же популярно рассказать о вейвлет-преобразовании? :))
А могли бы вы столь же популярно рассказать о вейвлет-преобразовании? :))
+7
Плюсую вейвлет-преобразование!
Желательно дискретное, и с реальными примерами кода.
На википедии и в других местах написано очень много теории, и я вроде даже понял что это такое, но не нашёл ни одного алгоритма с доступным описанием (в отличие от fft), чтобы просто взять и попробовать.
Желательно дискретное, и с реальными примерами кода.
На википедии и в других местах написано очень много теории, и я вроде даже понял что это такое, но не нашёл ни одного алгоритма с доступным описанием (в отличие от fft), чтобы просто взять и попробовать.
+7
Вот примеры кода с пояснением как именно работает преобразование на практике — это то, что нужно! Голую математику — в лес! у меня есть коспекты по высшей математике в вузе, я отлично сдал экзамены, даже условно понимаю зачем оно надо, но КАК оно работает я не понял до конца и так и не научился применять в произвольном реальном случае. Вот именно это и нужно. За такое объснение был бы очень благодарен.
Мне как-то товарищ недавно объяснил на пальцах ПИД регулятор и я наконец-то понял как реальные данные связать и обработать. До этого формулы были отдельно, а реальные данные отдельно и воедино никак не собирались хоть ты тресни.
Мне как-то товарищ недавно объяснил на пальцах ПИД регулятор и я наконец-то понял как реальные данные связать и обработать. До этого формулы были отдельно, а реальные данные отдельно и воедино никак не собирались хоть ты тресни.
+1
Обьясните и мне про ПИД, плиз
0
С вейвлетами я знаком гораздо хуже :), но тема действительно интересная, так что если я со временем наберусь сил в ней основательно разобраться, то такую статью безусловно напишу. Но едва ли в ближайший месяц-два, к сожалению.
0
Как в mp3 преобразовывают данные, что фреймы идут с перехлёстом 50%, а коэффициентов во фрейме ровно половинное число отсчётов?
0
А я ведь понимал всё это в универе! А прочитал вот эту статью и иллюстрировать ощущения могу только картинкой из «ёжика в тумане».
+8
Вполне милая статья, содержит основные позиции. Как универская шпора)
Меня вот только всегда смущали интерпретации типа «утечки спектра». Ограничив сигнал по времени мы получаем сигнал, ограниченный по времени (КО). Его спектр вполне себе определен. Радиоимпульс конечной длительности — это не просто синусоида. Это полноценный сигнал со спектром sinc, лежащий в основе большинства радиосистем (ФМ-2 и т.п.). Если вы этот радиоимпульс умножили на неравномерное окно — получили третью функцию, с третьим спектром.
Разговоры об «утечке спектра» возникают когда сделав FFT отрезка сигнала люди пытаются ответить на вопрос «А какой был бы спектр, если бы этот сигнал был бесконечно засемплирован?». Это отдельная задача, которую можно решать. Только это нужно подчеркивать и не вводить слушателя в заблуждения о наличии пороков у преобразования. Оно от этого не ломается)
Меня вот только всегда смущали интерпретации типа «утечки спектра». Ограничив сигнал по времени мы получаем сигнал, ограниченный по времени (КО). Его спектр вполне себе определен. Радиоимпульс конечной длительности — это не просто синусоида. Это полноценный сигнал со спектром sinc, лежащий в основе большинства радиосистем (ФМ-2 и т.п.). Если вы этот радиоимпульс умножили на неравномерное окно — получили третью функцию, с третьим спектром.
Разговоры об «утечке спектра» возникают когда сделав FFT отрезка сигнала люди пытаются ответить на вопрос «А какой был бы спектр, если бы этот сигнал был бесконечно засемплирован?». Это отдельная задача, которую можно решать. Только это нужно подчеркивать и не вводить слушателя в заблуждения о наличии пороков у преобразования. Оно от этого не ломается)
+2
Утечка спектра — вполне признанный термин. Хорошо демонстрирует границы применимости теоремы Котельникова.
Сигнал ограничен во времени => спектр растекается (см. Benedicks's theorem). Спектр растекается => невозможно применить теорему Котельникова.
Сигнал ограничен во времени => спектр растекается (см. Benedicks's theorem). Спектр растекается => невозможно применить теорему Котельникова.
-1
Я не спорю, что такое явление есть.
Я лишь говорю, что не стоит преподносить это как недостаток ПФ:
«На практике, однако, мы не можем применять ни FT ни DTFT напрямую, поскольку оба этих преобразования получают на вход сигнал определенный от минус до плюс бесконечности.»
Любой сигнал, по определению, функция с конечной энергией. И FT, и DTFT без проблем с ним работают, несмотря на то, что функция эта не равна нулю только на некотором интервале.
Безусловно, если мы берем периодическую функцию, ограничиваемся некоторым отрезком, берем ПФ, то итоговый спектр будет отличаться от спектра функции в бесконечных пределах — каждая составляющая спектра расползется по sinc'у. Но это частный случай, когда стоит задача определить спектр периодической функции, определенной в бесконечных пределах, по конечной выборке. Если функция и так ограничена, то никакой утечки спектра может и не быть. Я ратую за то, чтобы оговаривали задачу, перед тем как её решали, иначе это читателя только запутывает.
Я лишь говорю, что не стоит преподносить это как недостаток ПФ:
«На практике, однако, мы не можем применять ни FT ни DTFT напрямую, поскольку оба этих преобразования получают на вход сигнал определенный от минус до плюс бесконечности.»
Любой сигнал, по определению, функция с конечной энергией. И FT, и DTFT без проблем с ним работают, несмотря на то, что функция эта не равна нулю только на некотором интервале.
Безусловно, если мы берем периодическую функцию, ограничиваемся некоторым отрезком, берем ПФ, то итоговый спектр будет отличаться от спектра функции в бесконечных пределах — каждая составляющая спектра расползется по sinc'у. Но это частный случай, когда стоит задача определить спектр периодической функции, определенной в бесконечных пределах, по конечной выборке. Если функция и так ограничена, то никакой утечки спектра может и не быть. Я ратую за то, чтобы оговаривали задачу, перед тем как её решали, иначе это читателя только запутывает.
+3
Спасибо за комплимент :). С замечанием про утечку согласен, я просто исходил из предположения что статью будет читать более-менее обычный человек, который будет пытаться «находить» или «измерять» определенные частоты в исходном сигнале, предполагая их аналогичными по смыслу частотам синусоидальных сигналов. На Хабре было несколько статьей подобного плана, описывающих эксперименты с Фурье и Matlab-ом и я попробовал отталкиваться от примерно схожей схемы мышления. Но вышло похоже действительно переупрощенно, так что я постарался подправить текст чтобы сделать его более корректным.
-1
Матлаб — это исследовательский инструмент математика. Гораздо интереснее нормальный алгоритм, который можно превратить в код
0
Ну так чистый концентрированный алгоритм — это формулы, которые вы не любите.
0
Мне не нужен дистиллят. Мне нужно «мясо». Не святой дух формул, а алгоритм согласно его определению «Алгори́тм — набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное число действий.»
Формулы я признаю практически полезными, когда они записаны в виде конструкции любого языка программирования. Почему? Математика — это инструмент абстракции, поэтому перед ее практическим применением нужно сделать привязку к особенностям реального мира. Объяснив на красивом стройном ряде формул принцип, нужно спуститься с небес математики на грешную землю физики и инженерии и применить знания на практике. Только тогда формула станет полезной.
Я сам часто цитирую фразу «нет ничего практичнее хорошей теории», но теория хороша тогда, когда она не слишком оторвана от реальности.
В реальности вычисление производной или интеграла в символьном виде — практически невообразимо сложная алгоритмическая задача. Поэтому, например, интеграл на практике в дискретном цифровом мире является по сути вполне удобным сложением в цикле. И вот тут уже легко оценить красоту — сложное мат. преобразование красиво и вычислительно дешево дает практически ценный результат.
В рамках фестиваля 360 градусов в Политехе показывали хороший фильм — «Чувственная математика» — гениальные математики на пальцах для зрителя показывали и объясняли сложнейшие вещи так, что ими невольно проникаешься. Это искусство, которое востребовано в жизни на каждом шагу.
Формулы я признаю практически полезными, когда они записаны в виде конструкции любого языка программирования. Почему? Математика — это инструмент абстракции, поэтому перед ее практическим применением нужно сделать привязку к особенностям реального мира. Объяснив на красивом стройном ряде формул принцип, нужно спуститься с небес математики на грешную землю физики и инженерии и применить знания на практике. Только тогда формула станет полезной.
Я сам часто цитирую фразу «нет ничего практичнее хорошей теории», но теория хороша тогда, когда она не слишком оторвана от реальности.
В реальности вычисление производной или интеграла в символьном виде — практически невообразимо сложная алгоритмическая задача. Поэтому, например, интеграл на практике в дискретном цифровом мире является по сути вполне удобным сложением в цикле. И вот тут уже легко оценить красоту — сложное мат. преобразование красиво и вычислительно дешево дает практически ценный результат.
В рамках фестиваля 360 градусов в Политехе показывали хороший фильм — «Чувственная математика» — гениальные математики на пальцах для зрителя показывали и объясняли сложнейшие вещи так, что ими невольно проникаешься. Это искусство, которое востребовано в жизни на каждом шагу.
0
Вы пишете
А потом сразу после этого определяете , где
, где  — угловая частота.
— угловая частота.
Например в наших ВУЗах почему-то часто используют нормировку преобразования Фурье определяющую спектр в терминах угловой частоты (радианов в секунду). Я буду использовать более удобную западную формулировку, определяющую спектр в терминах обычной частоты (герцах).
А потом сразу после этого определяете
 , где
, где  — угловая частота.
— угловая частота.+4
Да нет, он сразу после этого определяет  , где
, где  — обычная частота. Тоже, кстати, ошибка, но несколько другого рода.
— обычная частота. Тоже, кстати, ошибка, но несколько другого рода.
 , где
, где  — обычная частота. Тоже, кстати, ошибка, но несколько другого рода.
— обычная частота. Тоже, кстати, ошибка, но несколько другого рода.+1
Согласен, но просто, чтобы никого не запутывать, обычную частоту лучше обозначать через  , а не
, а не  .
.
 , а не
, а не  .
.+5
Согласен, спасибо за замечание. Попробую подправить позднее
0
Ну f же привычнее, что за преклонение перед греческим алфавитом. Хотя тут оно будет конфликтовать с f(t). Но это — скорее повод переименовать f(t) в более привычное x(t).
0
Скорее там не omega, а просто w. Иногда используется в зарубежной литературе.
Меня скорее смущают некоторые ошибки в определениях (в формулах). Типа отсутствия j в показателе экспоненты в определении DFT.
Меня скорее смущают некоторые ошибки в определениях (в формулах). Типа отсутствия j в показателе экспоненты в определении DFT.
0
На этом сайте есть очень доходчивое и красивое объяснение betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/.
Попутно не менее доходчиво можно разобраться в комлексных числах. Вообще сайт достоин как минимум присутствия в закладках.
Попутно не менее доходчиво можно разобраться в комлексных числах. Вообще сайт достоин как минимум присутствия в закладках.
+7
Хочу только добавить, что на практике дискретное косинус-преобразование (DCT) используется чаще, т.к. работает только с действительными числами.
0
Есть предложение — описать DCT и его преимущества по отношению к FFT. Если только я не пропустил такую статью.
+1
Хочу только добавить, что на практике дискретное косинус-преобразование (DCT) используется чаще, т.к. работает только с действительными числами.Эти преобразования не взаимозаменяемы и дают разный результат. FFT прекрасно работает с действительными числами, поскольку они являются частным случаем комплексных (с мнимой частой равной нулю). Для чисто действительных последовательностей на практике используются специальные версии алгоритмов, известные как RFFT или преобразование Хартли (которое, в отличие от DCT, можно привести к FFT и наоборот).
0
Замечания.
1. Частота в герцах в большинстве книг и в википедии (статья «частота») обозначается буквой f (ню), а угловая частота — буквой омега.
2. Децибелы автором определены по мощности, а график дан для сигнала-функции. В последнем случае надо десятичные логарифмы умножать на 20.
3. На 3-ем графике сверху по горизонтальной оси проставлена частота омега, а отметки некоторой граничной частоты даны как fсит.
4. На графике синусоиды отмечена амплитуда а. Формула этой синусоиды содержит амплитуду, равную 1.
5. Несдвинутая дельта-функция имеет при t = 0 бесконечное значение, поэтому вместо термина «амплитуда дельта-функции» точнее использовать понятие коэффициента при дельта-функции.
6. Прямоугольная «выделяющая» функция на графике спектра имеет граничную частоту 1/2T, а не 1/T.
7. Сигнал на выходе реального ЦАП действительно имеет вид ступенек (см. Кучумов А.И. Электроника и схемотехника", М., 2011)
8. На графиках желательно указывать обозначения по горизонтальной оси.
Цель этих замечаний — улучшить Вашу работу.
1. Частота в герцах в большинстве книг и в википедии (статья «частота») обозначается буквой f (ню), а угловая частота — буквой омега.
2. Децибелы автором определены по мощности, а график дан для сигнала-функции. В последнем случае надо десятичные логарифмы умножать на 20.
3. На 3-ем графике сверху по горизонтальной оси проставлена частота омега, а отметки некоторой граничной частоты даны как fсит.
4. На графике синусоиды отмечена амплитуда а. Формула этой синусоиды содержит амплитуду, равную 1.
5. Несдвинутая дельта-функция имеет при t = 0 бесконечное значение, поэтому вместо термина «амплитуда дельта-функции» точнее использовать понятие коэффициента при дельта-функции.
6. Прямоугольная «выделяющая» функция на графике спектра имеет граничную частоту 1/2T, а не 1/T.
7. Сигнал на выходе реального ЦАП действительно имеет вид ступенек (см. Кучумов А.И. Электроника и схемотехника", М., 2011)
8. На графиках желательно указывать обозначения по горизонтальной оси.
Цель этих замечаний — улучшить Вашу работу.
+4
Спасибо за конструктивную критику!
1,3. Согласен. Я привык f обозначать функцию и стремился избежать путаницы, но действительно стоило упомянуть об этой детали и использовать более широко распространенные обозначения
2. Не согласен. Как раз наоборот, для амплитуды нужно умножать на 10, а для мощности — на 20. В первом случае — потому что ДЕЦИбелл, а во втором — потому что мощность есть квадрат амплитуды, а логарифм квадрата есть удвоенный логарифм
4,5,6. Исправлено
7. Не согласен, поскольку, во-первых, в большинстве современных ЦАПов (сигма-дельта) вообще всего 2 цифровых уровня сигнала на «цифровом» выходе, а во-вторых, при подобном подходе у ЦАПа получаются сильно субоптимальные характеристики. Так Кучумов в данном случае переупрощает.
1,3. Согласен. Я привык f обозначать функцию и стремился избежать путаницы, но действительно стоило упомянуть об этой детали и использовать более широко распространенные обозначения
2. Не согласен. Как раз наоборот, для амплитуды нужно умножать на 10, а для мощности — на 20. В первом случае — потому что ДЕЦИбелл, а во втором — потому что мощность есть квадрат амплитуды, а логарифм квадрата есть удвоенный логарифм
4,5,6. Исправлено
7. Не согласен, поскольку, во-первых, в большинстве современных ЦАПов (сигма-дельта) вообще всего 2 цифровых уровня сигнала на «цифровом» выходе, а во-вторых, при подобном подходе у ЦАПа получаются сильно субоптимальные характеристики. Так Кучумов в данном случае переупрощает.
+1
Боже, какой же я тупой…
0
Тема окажется не полной без ссылок на используемые сегодня реализации БПФ и так же хотелось услышать Ваши комментарии о этих реализациях.
А сам я начну с исторической реализации FFTPACK (http://www.netlib.org/fftpack/, эта реализация FFT на Fortran. А есть ли реализации на других языках?
А сам я начну с исторической реализации FFTPACK (http://www.netlib.org/fftpack/, эта реализация FFT на Fortran. А есть ли реализации на других языках?
+1
Года два-три назад наелся я с этой библиотекой. Версия, что была по умолчанию в ubuntu содержала баги и библиотека вела себя не так, как полагается по документации. Использование последних версий библиотеки мои проблемы решило. Так что хоть fftw «одна из стандартных библиотек» будьте осторожны при её использовании.
P.S.: Кстати эти баги я искал интересно. У меня octave выдавал физически некорректные цифры на тестовых данных (которые на матлабе давали корректные значения + руками эти корректные значения были проверены). Из вывода промежуточных данных стало ясно что шалит fft преобразование. Я написал скрипт который брал эталонный вывод из matlab-а, а потом сравнивал с выводом из octave (который этот скрипт собирал с разными версиями fftw). Обнаружил в какой версии fftw «что-то сломалось» и в какой починилось. Потом с нужной версией fftw свой бинарник и линковал.
P.S.: Кстати эти баги я искал интересно. У меня octave выдавал физически некорректные цифры на тестовых данных (которые на матлабе давали корректные значения + руками эти корректные значения были проверены). Из вывода промежуточных данных стало ясно что шалит fft преобразование. Я написал скрипт который брал эталонный вывод из matlab-а, а потом сравнивал с выводом из octave (который этот скрипт собирал с разными версиями fftw). Обнаружил в какой версии fftw «что-то сломалось» и в какой починилось. Потом с нужной версией fftw свой бинарник и линковал.
0
Да, кстати. Быстрое фурье-преобразование — это целая маленькая наука, без которой обработка обработка многомерных массивов (например, изображений) была бы очень затруднительна
0
Я уже пробовал, но попробую еще раз. С чего можно начать идиоту, который провтыкал всю высшую математику, и до сих пор не понимает практического назначения интегралов и логарифмов?
0
Хм. Назначение интегралов и логарифмов мы проходили в школе. Первые в 11 классе (или в 10 — не помню), вторые пораньше (9, 8???).
Если такие понятия непонятны — начать со чтения школьных учебников, википедии, сайтов обучающих навалом.
А можно я вас спрошу — а вам сейчас зачем понадобились те и другие? Какие проблемы в жизни вы собираетесь с новыми знаниями решить?
Почему спрашиваю — как правило «провтыкиваются» или «не прилипают» те знания, которые непонятно где в жизни применить.
Если такие понятия непонятны — начать со чтения школьных учебников, википедии, сайтов обучающих навалом.
А можно я вас спрошу — а вам сейчас зачем понадобились те и другие? Какие проблемы в жизни вы собираетесь с новыми знаниями решить?
Почему спрашиваю — как правило «провтыкиваются» или «не прилипают» те знания, которые непонятно где в жизни применить.
0
спасибо за экскурс!
может Вы могли бы просветить, чем отличаются друг от друга различные ЦАП?
и в сторону каких ЦАП смотреть если используется большой поток данных?
может Вы могли бы просветить, чем отличаются друг от друга различные ЦАП?
и в сторону каких ЦАП смотреть если используется большой поток данных?
+1
Частотой дискретизации (полосой частот), разрядностью (динамическим диапазоном), уровнем шума, стоимостью
Что подразумевается под «большим потоком данных» и во что его предполагается преобразовывать?
Что подразумевается под «большим потоком данных» и во что его предполагается преобразовывать?
0
подразумевается наличие постоянного аудиосигнала АЦП- процессор -ЦАП, одновременно с ним вывод с DAW дюжины дорожек (желательно на разные каналы) и возможность стороннего подключения других цифровых устройств
0
Вам нужно определиться с числом каналов, полосой частот, динамическим диапазоном и желаемым уровнем нелинейных искажений в аналоговом сигнале и после этого просто смотреть на подходящие модели и выбирать наиболее удобную.
В плане размера потока цифровых данных, простую работу с аудиопотоком (если не надо что-то хитрое вычислять) сегодня осилит даже микроконтроллер :). Работа с тем же USB может требовать намного большего потока данных.
Но Вам лучше к специалистам обратиться, мои познания больше теоретические чем практические
В плане размера потока цифровых данных, простую работу с аудиопотоком (если не надо что-то хитрое вычислять) сегодня осилит даже микроконтроллер :). Работа с тем же USB может требовать намного большего потока данных.
Но Вам лучше к специалистам обратиться, мои познания больше теоретические чем практические
0
Однако реальные доступные нам сигналы всегда имеют конечную длину — что делать? Для решения этой проблемы в FT и DTFT конечный сигнал просто дополняют слева и справа на бесконечность нулями.Это в корне неверно.
О дополнении нулями можно говорить, когда речь идёт о линейной свёртке посредством FFT (нулями дополняется импульсная характеристика фильтра). Здесь же мы имеем бесконечное дублирование:

Что позволяет ограничить спектр снизу и произвести вычисление только в рамках используемого окна. А преобразование как было бесконечным, так и осталось — и результат преобразования будет также бесконечным и также циклическим.
А бесконечно оно и циклично в силу бесконечности и цикличности функций синус и косинус. Вот если бы речь шла о вейвлет-преобразованиях — тогда да, дополнение нулями имеет место быть, поскольку вейвлет имеет компактную форму by design (собственно по этой причине вейвлет-преобразование и появилось).
+2
Если мы сделаем прямое БПФ, линейно сдвинем фазы, не трогая амплитуды, а затем сделаем обратное БПФ, то будем иметь уже такое:
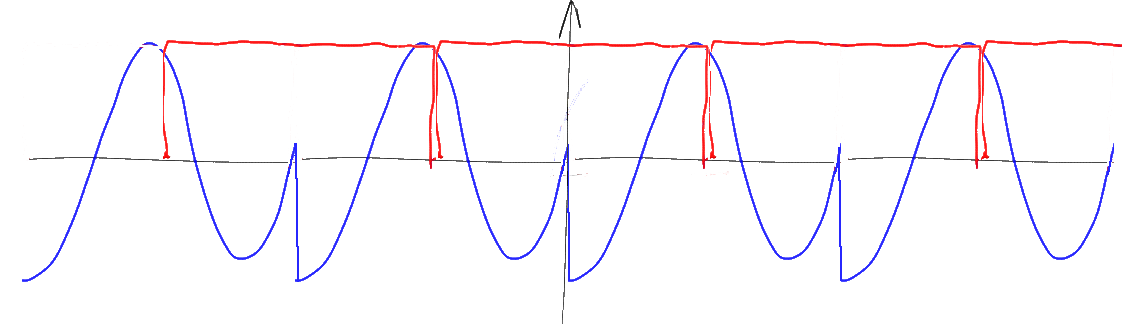

0
refridgerator, Вы не правы. Вы повторяете распространенную ошибку основанную на наивной интерпретации преобразования Фурье
Да, это верно что синус и косинус бесконечны и цикличны. Но проблема состоит в том что невозможно напрямую вычислить интеграл, скажем, от произведения двух синусов на действительной прямой. Я сейчас не буду вдаваться в функциональный анализ, но емнип любая попытка построения подобного обобщения все равно так или иначе идет через рассмотрение интегралов на конечных интервалах или (в общем случае) компактных многообразиях (что в данном контексте означает тот же ноль на бесконечности) и для практических вычислений подобные обобщения бесполезны. Кроме того измерить бесконечно длинный сигнал невозможно
А вот у финитной функции преобразование Фурье вычислить можно. И как я в статье постарался расписать, если мы домножим бесконечную функцию на «окно» которое сделает функцию пригодной для вычислений, то это внесет определенные искажения, но принципиально результат не изменит. Нужно просто правильно понимать какие именно будут внесены искажения чтобы правильно анализировать результат который выдало преобразование Фурье. Поэтому, к слову говоря, и существуют разные оконные функции вносящие соответственно разные искажения — для разных задач удобен разный анализ. И в рамках этого подхода, пока мы работаем на действительной прямой, единственно верным подходом является дополнение нолями.
Далее, у Вас похоже есть совершенно неверное представление о том что прямое преобразование Фурье даст нам разложение функции на сумму синусов и косинусов. Любая конечная сумма синусов и косинусов бесконечна и периодична, следовательно обратное преобразование Фурье даст бесконечную и периодическую функцию «дублируя» окно. Это неверно. Дабы «в лоб» реконструировать исходную непрерывную функцию пришлось бы брать обратное НЕПРЕРЫВНОЕ же преобразование Фурье. Даже для финитного спектра результат непрерывного обратного ПФ включает в себя «бесконечную сумму» синусов и косинусов результат которой не обязан быть периодическим. Спектр же любой финитной функции (например, после применения «окна») вообще бесконечен и если Вы примените обратное ПФ к этому бесконечному спектру, то — сюрприз! — на выходе получите финитную функцию, обращенную в ноль вне некоторого отрезка.
Другими словами нельзя бездумно мешать и взаимозаменять дискретное и непрерывное преобразования Фурье и уж точно не стоит игнорировать наличие «бесконечной» части спектра делая обратное преобразование Фурье.
Для дискретных преобразований была создана вариация которая похожа на преобразование Фурье, но отличается от него. Она подразумевает рассмотрение функций заданных не на (бесконечной) действительной прямой а на окружности конечной длины. Это пространство можно рассматривать как модель пространства T-периодических функций на R для какого-то заданного наперед T и там получается свой «аналог» непрерывного и дискретного ПФ, но с заметно отличающимися свойствами обусловленными введенным нами искусственным ограничением T-периодичности. Но не надо мешать это специальное пространство со специальными свойствами с исходным «базовым» пространством функций заданных на действительной прямой. Это очень распространенная ошибка связанная с тем что ДПФ удобнее и «естественнее» определяется именно на этом специальном пространстве а дальше люди просто не замечают что непрерывное ПФ определено иначе.
Да, это верно что синус и косинус бесконечны и цикличны. Но проблема состоит в том что невозможно напрямую вычислить интеграл, скажем, от произведения двух синусов на действительной прямой. Я сейчас не буду вдаваться в функциональный анализ, но емнип любая попытка построения подобного обобщения все равно так или иначе идет через рассмотрение интегралов на конечных интервалах или (в общем случае) компактных многообразиях (что в данном контексте означает тот же ноль на бесконечности) и для практических вычислений подобные обобщения бесполезны. Кроме того измерить бесконечно длинный сигнал невозможно
А вот у финитной функции преобразование Фурье вычислить можно. И как я в статье постарался расписать, если мы домножим бесконечную функцию на «окно» которое сделает функцию пригодной для вычислений, то это внесет определенные искажения, но принципиально результат не изменит. Нужно просто правильно понимать какие именно будут внесены искажения чтобы правильно анализировать результат который выдало преобразование Фурье. Поэтому, к слову говоря, и существуют разные оконные функции вносящие соответственно разные искажения — для разных задач удобен разный анализ. И в рамках этого подхода, пока мы работаем на действительной прямой, единственно верным подходом является дополнение нолями.
Далее, у Вас похоже есть совершенно неверное представление о том что прямое преобразование Фурье даст нам разложение функции на сумму синусов и косинусов. Любая конечная сумма синусов и косинусов бесконечна и периодична, следовательно обратное преобразование Фурье даст бесконечную и периодическую функцию «дублируя» окно. Это неверно. Дабы «в лоб» реконструировать исходную непрерывную функцию пришлось бы брать обратное НЕПРЕРЫВНОЕ же преобразование Фурье. Даже для финитного спектра результат непрерывного обратного ПФ включает в себя «бесконечную сумму» синусов и косинусов результат которой не обязан быть периодическим. Спектр же любой финитной функции (например, после применения «окна») вообще бесконечен и если Вы примените обратное ПФ к этому бесконечному спектру, то — сюрприз! — на выходе получите финитную функцию, обращенную в ноль вне некоторого отрезка.
Другими словами нельзя бездумно мешать и взаимозаменять дискретное и непрерывное преобразования Фурье и уж точно не стоит игнорировать наличие «бесконечной» части спектра делая обратное преобразование Фурье.
Для дискретных преобразований была создана вариация которая похожа на преобразование Фурье, но отличается от него. Она подразумевает рассмотрение функций заданных не на (бесконечной) действительной прямой а на окружности конечной длины. Это пространство можно рассматривать как модель пространства T-периодических функций на R для какого-то заданного наперед T и там получается свой «аналог» непрерывного и дискретного ПФ, но с заметно отличающимися свойствами обусловленными введенным нами искусственным ограничением T-периодичности. Но не надо мешать это специальное пространство со специальными свойствами с исходным «базовым» пространством функций заданных на действительной прямой. Это очень распространенная ошибка связанная с тем что ДПФ удобнее и «естественнее» определяется именно на этом специальном пространстве а дальше люди просто не замечают что непрерывное ПФ определено иначе.
+1
Если я в чём и неправ — так это в том, что не указал явно, что речь идёт именно о дискретном преобразовании, считая это очевидным из контекста цитаты:
Спектр, полученный в результате дискретного преобразования, также будет дискретным, и над ним также можно выполнить обратное преобразование и получить исходный сигнал. Что у вас не получится, если вы будете использовать дополнение нулями.
Вообще, разницу между зацикливанием и дополнением нулями легко увидеть, если просто взять и посмотреть:
зацикливание:
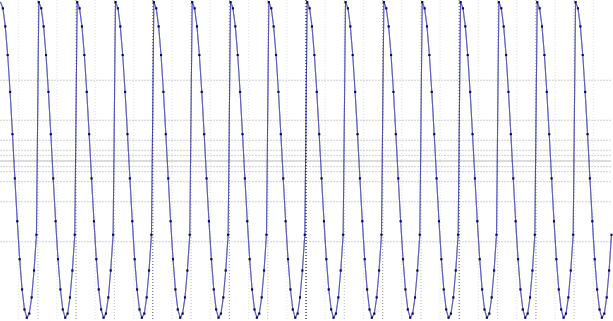
дополнение нулями:
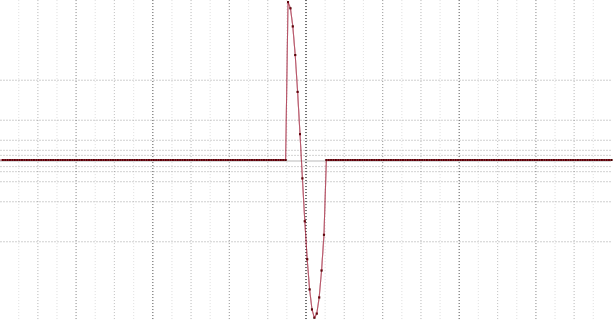
спектр обоих сигналов:

Видно, что в первом случае мы получили дискретный спектр, а во втором — непрерывный.
Однако реальные доступные нам сигналы всегда имеют конечную длину — что делать? Для решения этой проблемы в FT и DTFT конечный сигнал просто дополняют слева и справа на бесконечность нулями.Поскольку как только речь заходит о реальности, никаких непрерывных преобразований быть не может, поскольку мы должны выполнить его за конечное число вычислений, что доступно только на периодическом дискретном сигнале.
Спектр, полученный в результате дискретного преобразования, также будет дискретным, и над ним также можно выполнить обратное преобразование и получить исходный сигнал. Что у вас не получится, если вы будете использовать дополнение нулями.
Вообще, разницу между зацикливанием и дополнением нулями легко увидеть, если просто взять и посмотреть:
зацикливание:

дополнение нулями:

спектр обоих сигналов:

Видно, что в первом случае мы получили дискретный спектр, а во втором — непрерывный.
0
Поскольку как только речь заходит о реальности, никаких непрерывных преобразований быть не может, поскольку мы должны выполнить его за конечное число вычислений,
А в том и состоит прелесть ДПФ что дискретное приближение к результату непрерывного ПФ можно вычислить с любой желаемой точностью через ДПФ с дополнением нулями :).
что доступно только на периодическом дискретном сигнале.
Неверно. На любом дискретном сигнале конечной длины. Не обязательно периодическим.
Спектр, полученный в результате дискретного преобразования, также будет дискретным, и над ним также можно выполнить обратное преобразование и получить исходный сигнал. Что у вас не получится, если вы будете использовать дополнение нулями.
Прекрасно все получится. Обратное преобразование от спектра посчитанного на сигнале с дополнением нолями просто даст исходный сигнал дополненный нолями. Собственно это просто вопрос того как интерпретировать набор чисел, а сам набор чисел и само применяемое к нему преобразование то одно и то же и результат и обратимость этого преобразования, естественно, от выбранной интерпретации не зависят.
Видно, что в первом случае мы получили дискретный спектр, а во втором — непрерывный.
Видно что этот дискретный спектр — это просто подмножество непрерывного :). При этом если выбранный нами наугад период сигнала не соответствует настоящему периоду, то мы еще и потеряем при этом информацию содержавшуюся в исходном сигнале. Зачем?
0
Видно что этот дискретный спектр — это просто подмножество непрерывного.Существует бесконечное множество непрерывных спектров, подмножеством которых является конкретно этот дискретный. И в контексте Фурье-анализа конкретно этот непрерывный спектр — вовсе не наилучший.
0
В контексте Фурье-анализа нас могут интересовать разные свойства сигнала и да, для разных задач целесообразно выбирать разные оконные функции которые дадут разные спектры. Но любой из этих спектров будет лучше Вашего «дискретного» для целей анализа спектра исходного непрерывного сигнала за исключением одного-единственного случая когда сигнал периодический, Вы верно угадаете истинный период сигнала и он окажется кратным периоду дискретизации.
0
Множество оконных функций не покрывает множество непрерывных спектров, подмножеством которых является единственный дискретный.
0
Простите, я не понимаю к чему Вы ведете и что пытаетесь доказать.
Если у нас есть скажем синус неизвестной частоты и фазы, то непрерывный спектр посчитанный через приближение дискретным с дополнением нолями позволит определить его частоту, амплитуду и фазу, а дискретный «периодический» с повторением или зеркалированием сигнала, как правило, этого сделать не позволит.
Если у нас есть скажем синус неизвестной частоты и фазы, то непрерывный спектр посчитанный через приближение дискретным с дополнением нолями позволит определить его частоту, амплитуду и фазу, а дискретный «периодический» с повторением или зеркалированием сигнала, как правило, этого сделать не позволит.
0
Я веду к тому, что дополнение нулями при рассмотрении БПФ — некорректно и к тому же ещё и бессмысленно, поскольку не добавляет никакой новой информации. Если же рассматривать задачу аппроксимации спектра — так это совсем другая задача.
Если использовать дополнение нулями для анализа спектра оконных функций — так и это другая задача, а сами оконные функции — совершенно самостоятельный инструмент, вовсе не являющийся необходимым условием как для непрерывного, так и для дискретного ПФ.
Если использовать дополнение нулями для анализа спектра оконных функций — так и это другая задача, а сами оконные функции — совершенно самостоятельный инструмент, вовсе не являющийся необходимым условием как для непрерывного, так и для дискретного ПФ.
0
Я ниже привел простой и наглядный пример. Можете поиграть с параметром FFT_SAMPLES чтобы понять «бессмысленно» ли это. Hint: без дополнения нолями оценка частоты сигнала F=10 Гц, с дополнением 6 нолями F=12.5 Гц, для 8182 нолей F=14.44 Гц. Насчет корректности я советую сравнить точность результата с дополнением нолями с точностью результата с периодическим дополнением и немного подумать, если уж Вам из моих объяснений так и не стало понятно почему дополнять нолями не только корректно, но и единственно корректно.
0
продемонстрируйте.что доступно только на периодическом дискретном сигнале.Неверно. На любом дискретном сигнале конечной длины. Не обязательно периодическим.
0
Что продемонстрировать? Взяли кусок сигнала, оцифровали — получили набор чисел. Дополнили нолями — получили второй набор чисел. Взяли ДПФ — получили третий набор чисел. Взяли обратное ДПФ — получили обратно второй набор чисел с дополнением нолями. Убрали дополнение нолями — получили первый набор чисел. Что именно в указанной цепочке у Вас вызывает сомнения?
0
Ну если конкретно тут —
чёрта лысого.
Дополнили нолями — получили второй [бесконечный] набор чисел. Взяли ДПФ ...А вот и не возьмёте, для ДПФ нужен конечный набор чисел. А если при ДПФ вы эти дополненные нули игнорируете — зачем их тогда вообще добавлять? С тем же результатом можно что угодно добавить, хоть нули, хоть единицы, хоть
0
Эм, зачем? Дополнили конечным числом нолей. Чем больше добавим, тем точнее будет дискретное приближение непрерывного спектра (точнее, тем больше будет в нём точек), но можно ограничиться любым их количеством. И да, в ДПФ добавление конечного числа нулей к входному сигналу меняет результат (делает его более детализованным).
0
Конкретно в моём примере это будет приближение вовсе не к тому спектру, который был изначально.
0
Ох. Давайте глянем на простой пример
Результат:

Изначальный спектр (синус) — дельта-функция на F=15.32 Гц, показана красной линией на обеих графиках
Левый спектр (№1) построен дополнением нолями, правый (№2) — периодическим дополнением.
Так Вы говорите, правый спектр — это лучшее приближение к правильному, а нолями (слева) дополнять неправильно, да :D?
import numpy as np
import matplotlib.pyplot as plt
def test():
DISCR_FREQ = 100.0
TEST_FREQ = 15.32
TEST_SAMPLES = 10
FFT_SAMPLES = 1024
data = [np.sin(TEST_FREQ*np.pi*2 * i/DISCR_FREQ) for i in range(TEST_SAMPLES)]
data1 = np.zeros(shape=(FFT_SAMPLES,))
data1[0:len(data)] = data
data2 = np.zeros(shape=(FFT_SAMPLES,))
for i in range(len(data2)):
data2[i] = data[i % TEST_SAMPLES]
fft1 = np.fft.rfft(data1)
fft2 = np.fft.rfft(data2)
faxis = np.linspace(0, DISCR_FREQ/2, num=FFT_SAMPLES/2+1)
plt.figure()
plt.subplot(121)
plt.plot(faxis, np.absolute(fft1))
plt.plot([TEST_FREQ,TEST_FREQ], plt.axis()[2:4], 'r--' )
plt.subplot(122)
plt.plot(faxis, np.absolute(fft2))
plt.plot([TEST_FREQ,TEST_FREQ], plt.axis()[2:4], 'r--')
print "Freq 1=", faxis[np.argmax(np.absolute(fft1))]
print "Freq 2=", faxis[np.argmax(np.absolute(fft2))]
plt.show()
Результат:

Изначальный спектр (синус) — дельта-функция на F=15.32 Гц, показана красной линией на обеих графиках
Левый спектр (№1) построен дополнением нолями, правый (№2) — периодическим дополнением.
Так Вы говорите, правый спектр — это лучшее приближение к правильному, а нолями (слева) дополнять неправильно, да :D?
+1
В правом графике значение в точке 15.32 попросту не определено, поскольку находится в промежутке между соседними дискретными. Но его можно найти интерполяцией. Например, линейной. Или свёрткой со спектром функции sinc. Или свёрткой со спектром прямоугольного окна, что у вас и получилось на левом графике.
0
В правом графике прекрасно себе определено значение в точке 15.33203125 и оно практически равно нулю, как и в соседних точках. Между чем и чем прикажете интерполировать? И как же так получается что «некорректное и бессмысленное» дополнение нолями дает правильный ответ причем очень простым и удобным способом не требующим никакой интерполяции или свертки?
0
Оно не определено. Дублирование сигнала перед БПФ — это лишь простой способ продемонстрировать дискретность спектра, а вовсе не инструкция к применению. А эти нули как раз-то и позволяют избавиться от бесконечного количества вычислений. Точно так же, как умножение любого числа на ноль даёт ноль. И точно так же, как и вычислив значение синуса в одной точке 0.1, мы одновременно вычисляем значение синуса во всех точках 0.1+2*pi*k
0
Вы одновременно защищаете так много тезисов и так легко переключаетесь между ними что я предлагаю остановиться и зафиксировать два простых момента.
1. Дописывание нолей — простой и надежный практический способ запихнуть в FFT дискретный сигнал длина которого не равна 2^n, а так же рассчитать спектр с любым желаемым числом точек.
1.1. Не будем пока фиксироваться на том «правильно ли это теоретически», ограничимся констатацией того что это удобно в использовании и на практике дает правильный результат
1.2. К слову говоря, в np.fft из моего примера это штатная фича которую не требуется имплементировать самому
2. Дополнение нолями в последовательности ДПФ -> обратное ДПФ никак не мешает в точности восстановить исходную последовательность чисел
Хорошо? Потому что Вы вроде как с этими двумя пунктами вначале спорили, а потом промолчали в отношении моих примеров и объяснений доказывающих эти два тезиса.
Зафиксировав эти два момента я Вам предлагаю дальше внятно объяснить свою мысль о «дискретности спектра» и пояснить что Вы предполагаете исходя из этого использовать в практических вычислениях.
1. Дописывание нолей — простой и надежный практический способ запихнуть в FFT дискретный сигнал длина которого не равна 2^n, а так же рассчитать спектр с любым желаемым числом точек.
1.1. Не будем пока фиксироваться на том «правильно ли это теоретически», ограничимся констатацией того что это удобно в использовании и на практике дает правильный результат
1.2. К слову говоря, в np.fft из моего примера это штатная фича которую не требуется имплементировать самому
2. Дополнение нолями в последовательности ДПФ -> обратное ДПФ никак не мешает в точности восстановить исходную последовательность чисел
Хорошо? Потому что Вы вроде как с этими двумя пунктами вначале спорили, а потом промолчали в отношении моих примеров и объяснений доказывающих эти два тезиса.
Зафиксировав эти два момента я Вам предлагаю дальше внятно объяснить свою мысль о «дискретности спектра» и пояснить что Вы предполагаете исходя из этого использовать в практических вычислениях.
0
1. Простой — да. Надёжный — да, если это ядро FIR-фильтра и нет, если это сигнал для гармонического анализа.
2. Дополнение конечным количеством — да, равно как и любыми другими отличными от нуля числами. Дополнение бесконечным количеством, чтобы объяснить переход от конечного во времени сигнала к бесконечному и непрерывному преобразованию — нет.
Если под доказательством вы подразумеваете невозможность взятия интеграла синуса на бесконечности, то я счёл его некорректным, поскольку ПФ от синуса прекрасно берётся.
Я не вижу более внятного объяснения «дискретности спектра», если мы и так уже имеем дискретное преобразование над дискретным сигналом, дающим на выходе дискретный спектр.
Поскольку значения между дискретным значениями не определены по определению (вообще, а не только для дискретного спектра), мы можем определить их (при необходимости) одним из инструментов интерполяции.
2. Дополнение конечным количеством — да, равно как и любыми другими отличными от нуля числами. Дополнение бесконечным количеством, чтобы объяснить переход от конечного во времени сигнала к бесконечному и непрерывному преобразованию — нет.
Если под доказательством вы подразумеваете невозможность взятия интеграла синуса на бесконечности, то я счёл его некорректным, поскольку ПФ от синуса прекрасно берётся.
Я не вижу более внятного объяснения «дискретности спектра», если мы и так уже имеем дискретное преобразование над дискретным сигналом, дающим на выходе дискретный спектр.
Поскольку значения между дискретным значениями не определены по определению (вообще, а не только для дискретного спектра), мы можем определить их (при необходимости) одним из инструментов интерполяции.
0
ОК. Тогда давайте вернемся к исходному примеру.
1. Обратите внимание на то что результат анализа спектра при дописывании нолей соответствует ожидаемому.
2. Поскольку Вы утверждаете что этот метод «не надежный» то предложите конкретный контр-пример иллюстрирующий эту ненадежность
3. Предложите пожалуйста альтернативный метод «интерполяции» который будет работать надежнее
Далее, про дискретные и непрерывные сигналы. В моем примере мы имеем чистый синусоидальный сигнал информация о котором доступна на отрезке времени длиной 0.01 секунда.
Вы утверждаете что дискретизация «портит» этот сигнал и делает его принципиально отличным от непрерывного синуса известного на том же временном промежутке. Давайте проведем простой мысленный эксперимент: будем увеличивать количество точек дискретизации. Вместо 10 точек возьмем 100, 1.000, 10.000 и так далее.
4. Я смею утверждать что дискретный сигнал описывающий нашу синусоиду с помощью измерения сигнала в 10^n точек равномерно распределенных по нашему временному интервалу 0.01 сек является приближение непрерывного сигнала и при n стремящимся к бесконечности подобное дискретное приближение неотличимо мало от исходного непрерывного сигнала
5. Объясните пожалуйста почему спектр этого сигнала (что в Вашей «дискретной» модели что в моей с дописыванием нулей) при сколь угодно больших n (т.е. сколь угодно близком приближении к непрерывной функции) в диапазоне 0-50 Гц практически не меняется.
5.1. Напомню что в моей модели которую я Вам пытаюсь разжевать, это напрямую связано с тем что влияние «окна» на спектр относится к аналоговой части сигнала — т.е. тому факту что сигнал известен только на (аналоговом) отрезке длиною 0.01 секунда. Дискретизация же происходит уже после окна и дает другие эффекты.
1. Обратите внимание на то что результат анализа спектра при дописывании нолей соответствует ожидаемому.
2. Поскольку Вы утверждаете что этот метод «не надежный» то предложите конкретный контр-пример иллюстрирующий эту ненадежность
3. Предложите пожалуйста альтернативный метод «интерполяции» который будет работать надежнее
Далее, про дискретные и непрерывные сигналы. В моем примере мы имеем чистый синусоидальный сигнал информация о котором доступна на отрезке времени длиной 0.01 секунда.
Вы утверждаете что дискретизация «портит» этот сигнал и делает его принципиально отличным от непрерывного синуса известного на том же временном промежутке. Давайте проведем простой мысленный эксперимент: будем увеличивать количество точек дискретизации. Вместо 10 точек возьмем 100, 1.000, 10.000 и так далее.
4. Я смею утверждать что дискретный сигнал описывающий нашу синусоиду с помощью измерения сигнала в 10^n точек равномерно распределенных по нашему временному интервалу 0.01 сек является приближение непрерывного сигнала и при n стремящимся к бесконечности подобное дискретное приближение неотличимо мало от исходного непрерывного сигнала
5. Объясните пожалуйста почему спектр этого сигнала (что в Вашей «дискретной» модели что в моей с дописыванием нулей) при сколь угодно больших n (т.е. сколь угодно близком приближении к непрерывной функции) в диапазоне 0-50 Гц практически не меняется.
5.1. Напомню что в моей модели которую я Вам пытаюсь разжевать, это напрямую связано с тем что влияние «окна» на спектр относится к аналоговой части сигнала — т.е. тому факту что сигнал известен только на (аналоговом) отрезке длиною 0.01 секунда. Дискретизация же происходит уже после окна и дает другие эффекты.
0
1. Не факт. Пульсации в спектре сигнала из одной частоты лично я не могу назвать ожидаемыми.
2. Легко. Синусоида, период которой равен 15 семплам, при DFT=15 даст в спектре только одну составляющую. А при DFT=16 уже нет, особенно если она будет сдвинута по фазе.
3. Если бы передо мной встала такая задача, я бы в первую очередь попробовал кусочную кубическую интерполяцию между комплексными частотами в логарифмическом масштабе. Затем то же, но по логарифмическим амплитудам. Затем, возможно, и рациональную интерполяцию, но на бо́льшем количестве точек.
4,5 Это всё прямо следует из теоремы Котельникова.
5.1. А я напомню, что поскольку сигнал за пределами этого отрезка не определён, существует бесконечное множество спектров, сигналы с которыми конкретно в этом отрезке времени будут иметь одни и те же значения. И та частота, которую вы рассматриваете, вовсе не обязательно будет иметь в этих спектрах максимальную амплитуду.
2. Легко. Синусоида, период которой равен 15 семплам, при DFT=15 даст в спектре только одну составляющую. А при DFT=16 уже нет, особенно если она будет сдвинута по фазе.
3. Если бы передо мной встала такая задача, я бы в первую очередь попробовал кусочную кубическую интерполяцию между комплексными частотами в логарифмическом масштабе. Затем то же, но по логарифмическим амплитудам. Затем, возможно, и рациональную интерполяцию, но на бо́льшем количестве точек.
Вы утверждаете что дискретизация «портит» этот сигнал и делает его принципиально отличным от непрерывного синуса известного на том же временном промежутке.Не помню такого. В вопросе дискретизации непрерывных сигналов я придерживаюсь классической позиции Котельникова/Найквиста/Шеннона.
4,5 Это всё прямо следует из теоремы Котельникова.
5.1. А я напомню, что поскольку сигнал за пределами этого отрезка не определён, существует бесконечное множество спектров, сигналы с которыми конкретно в этом отрезке времени будут иметь одни и те же значения. И та частота, которую вы рассматриваете, вовсе не обязательно будет иметь в этих спектрах максимальную амплитуду.
0
1. Там все просто. Исходный спектр — две дельта-функции. На этапе когда идет обрезка непрерывного сигнала до кусочка длиной 0.01 сек дельты сворачиваются с sinc. Функция sinc не является финитной, поэтому sinc-и соответствующие плюсовой и минусовой частотам влияют друг на друга — это и дает смещение пика по амплитуде и частоте. При дискретизации дополнительно к этому sinc с «бесконечности» заворачивается алиасингом на «рабочий» диапазон, это дает зависимость от частоты дискретизации (небольшую при достаточно большой частоте дискретизации и стремящуюся к нулю при n->inf)
2. Прошу прощения, но к чему этот пример? Он может разве что служить свидетельством ненадежности Вашего метода — стоит неверно выбрать период и на выходе вместо ожидаемого единственного пика получаем мусор :D
3. Другими словами Вы бы наугад занимались эмпирикой, а на практике этого не делали, правильно?
4. В огороде бузина, а в Киеве дядька. При чем тут Котельников? Представьте что у Вас есть непрерывная функция (синус). Вообще без дискретизации, но обрезанная до отрезка длиной 0.01 сек. Я утверждаю что ее спектр (непрерывный) будет в точности тем который дает дискретное ПФ и поясняю это на примере бесконечного увеличения числа точек которыми задается функция. В терминах Котельникова я предлагаю бесконечно увеличить частоту дискретизации и посмотреть на предел к которому при этом стремится спектр получаемый в дискретном преобразовании.
5.1. Естественно. Только к чему Вы это?
2. Прошу прощения, но к чему этот пример? Он может разве что служить свидетельством ненадежности Вашего метода — стоит неверно выбрать период и на выходе вместо ожидаемого единственного пика получаем мусор :D
3. Другими словами Вы бы наугад занимались эмпирикой, а на практике этого не делали, правильно?
4. В огороде бузина, а в Киеве дядька. При чем тут Котельников? Представьте что у Вас есть непрерывная функция (синус). Вообще без дискретизации, но обрезанная до отрезка длиной 0.01 сек. Я утверждаю что ее спектр (непрерывный) будет в точности тем который дает дискретное ПФ и поясняю это на примере бесконечного увеличения числа точек которыми задается функция. В терминах Котельникова я предлагаю бесконечно увеличить частоту дискретизации и посмотреть на предел к которому при этом стремится спектр получаемый в дискретном преобразовании.
5.1. Естественно. Только к чему Вы это?
0
2. Вы просили пример, я его привёл.
3. Что значит наугад, какая эмпирика? Интерполяция вполне научна. А поиском частоты с максимальной амплитудой да, заниматься не приходилось, использую ДПФ совсем для других задач.
4. Вероятно при том, что пока частота синусоиды вдвое меньше частоты дискретизации, она восстанавливается без искажений. Видимо, я Вас не так понял.
4.1. т.е. Вы утверждаете, что непрерывный спектр синусоиды, обрезанный на произвольном интервале и дополненный нулями в бесконечность, в пределе будет равен спектру просто синусоиды?
5.1. К неоднозначности Фурье-анализа на ограниченном промежутке времени.
3. Что значит наугад, какая эмпирика? Интерполяция вполне научна. А поиском частоты с максимальной амплитудой да, заниматься не приходилось, использую ДПФ совсем для других задач.
4. Вероятно при том, что пока частота синусоиды вдвое меньше частоты дискретизации, она восстанавливается без искажений. Видимо, я Вас не так понял.
4.1. т.е. Вы утверждаете, что непрерывный спектр синусоиды, обрезанный на произвольном интервале и дополненный нулями в бесконечность, в пределе будет равен спектру просто синусоиды?
5.1. К неоднозначности Фурье-анализа на ограниченном промежутке времени.
0
2. Я просил пример где дополнение нулями не работает. А оно-то как раз в Вашем примере работает. Независимо от частоты сигнала и длительности периода наблюдения Вы получите sinc примерно соответствующий исходному сигналу. В отличие от наивной попытки посмотреть на дискретный спектр или дополнить сигнал периодически
3. Интерполяция бывает разной. Вы предлагаете выбрать интерполяционный метод наугад, по принципу «что больше нравится», а не «что здесь будет работать и какую погрешность можно ожидать»
4. Это верно только для дискретного сигнала бесконечной длины :).
4.1 Нет. Я утверждаю что спектр который выдает ДПФ при дополнении нолями и который я Вам показывал выше стремится к спектру непрерывной синусоиды обрезанной на наш интервал. То есть дискретизация не играет здесь существенной роли, а вот обрезка сигнала на (аналоговый) отрезок — играет. Как следствие если нас интересует спектр исходного непрерывного сигнала, то и смотреть надо на спектр получающийся на выходе ДПФ при дополнении исходного сигнала нолями.
5. Не Вы ли мне говорили чуть выше что все реальные сигналы ограничены :D? Идеальная реконструкция по Котельникову конечно требует бесконечной длины сигнала, но реальные конечные приближения легко дают хотя и не идеальную, но отличную аппроксимацию
3. Интерполяция бывает разной. Вы предлагаете выбрать интерполяционный метод наугад, по принципу «что больше нравится», а не «что здесь будет работать и какую погрешность можно ожидать»
4. Это верно только для дискретного сигнала бесконечной длины :).
4.1 Нет. Я утверждаю что спектр который выдает ДПФ при дополнении нолями и который я Вам показывал выше стремится к спектру непрерывной синусоиды обрезанной на наш интервал. То есть дискретизация не играет здесь существенной роли, а вот обрезка сигнала на (аналоговый) отрезок — играет. Как следствие если нас интересует спектр исходного непрерывного сигнала, то и смотреть надо на спектр получающийся на выходе ДПФ при дополнении исходного сигнала нолями.
5. Не Вы ли мне говорили чуть выше что все реальные сигналы ограничены :D? Идеальная реконструкция по Котельникову конечно требует бесконечной длины сигнала, но реальные конечные приближения легко дают хотя и не идеальную, но отличную аппроксимацию
0
2. Я привёл пример, в котором амплитуда зависит от фазы. Очевидно, так быть не должно.
3. Я ничего не говорил про выбор «наугад». Я говорил, что их бесконечное множество и оптимальный вариант будет разным в зависимости от задачи. Поэтому вы не вправе говорить, что дополнение нулями (что есть по сути прямоугольное окно) — единственно правильное решение. Оно может быть подходящим в одних случаях и совершенно неприемлемым в других.
4.1. Он стремится по той же причине, по которой и сам сигнал стремится, это само собой. Если сигналы совпадают, то и их спектры совпадают.
4,5 Как Вы сами и указали, если пространство закольцовано, бесконечность уже не требуется.
3. Я ничего не говорил про выбор «наугад». Я говорил, что их бесконечное множество и оптимальный вариант будет разным в зависимости от задачи. Поэтому вы не вправе говорить, что дополнение нулями (что есть по сути прямоугольное окно) — единственно правильное решение. Оно может быть подходящим в одних случаях и совершенно неприемлемым в других.
4.1. Он стремится по той же причине, по которой и сам сигнал стремится, это само собой. Если сигналы совпадают, то и их спектры совпадают.
4,5 Как Вы сами и указали, если пространство закольцовано, бесконечность уже не требуется.
0
2. А Вы, простите, не пробовали взять код который я привел выше и подставить туда изменение фазы :)? Вас ждет боооольшой сюрприз — амплитуда от фазы, как ни «странно», почти не зависит.
3. Если Вас интересует спектр непрерывной функции (после ее обрезки на доступный период измерений, конечно) то дополнение нолями дает именно его. Конечно это не единственный возможный вариант, но обычно именно этот является ожидаемым :).
4.5. Для закольцованного пространства любой синус с периодом не укладывающимся на кольце целое число раз не является «функцией со спектром ограниченным сверху» что требуется в теореме Котельникова. Это очень специальное пространство сильно отличающееся от R, я же говорю.
3. Если Вас интересует спектр непрерывной функции (после ее обрезки на доступный период измерений, конечно) то дополнение нолями дает именно его. Конечно это не единственный возможный вариант, но обычно именно этот является ожидаемым :).
4.5. Для закольцованного пространства любой синус с периодом не укладывающимся на кольце целое число раз не является «функцией со спектром ограниченным сверху» что требуется в теореме Котельникова. Это очень специальное пространство сильно отличающееся от R, я же говорю.
0
2. Пробовал много раньше. Почти — это субъективная оценка. Объективно не зависит — это когда вообще никак не зависит.
3. Ожидание — это субъективная оценка. Вы ожидаете одно, а я — совсем другое.
4.5. Согласен. Только в ДПФ ему взяться неоткуда.
3. Ожидание — это субъективная оценка. Вы ожидаете одно, а я — совсем другое.
4.5. Согласен. Только в ДПФ ему взяться неоткуда.
0
2. А с чего вдруг оно объективно должно вообще не зависеть? В указанном Вами примере максимальное отклонение по амплитуде от истинного — 8%, среднее — 1.4%. Возьмете более короткий отрезок измерения — погрешность будет больше. Возьмете более длинный — меньше. Это хорошо известное соотношение неопределенностей: чем короче отрезок, тем больше погрешность измерения. А так конечно вопрос точности субьективен, но на мой взгляд погрешность 10% для настолько маленького отрезка где едва укладывается один период — это весьма неплохо :).
4. Проще говоря, ваша позиция сводится к тому что размерность R^n равна n а «спектром» по определению называется результат ДПФ от заданного вектора чисел и это тоже n-мерный вектор комплексных чисел. Потому что вы оперируете с n-мерными векторами чисел абсолютно без какой-либо привязки к непрерывным функциям. К примеру у Вас вообще не существуют синусоидальные сигналы период которых не кратен шагу дискретизации. Вот нету их просто и всё. При этом Вы с чего-то решили что можете поучать других (!) о том что правильно и что не правильно делать. Шикарно. Давайте сворачивать на этом дискуссию.
4. Проще говоря, ваша позиция сводится к тому что размерность R^n равна n а «спектром» по определению называется результат ДПФ от заданного вектора чисел и это тоже n-мерный вектор комплексных чисел. Потому что вы оперируете с n-мерными векторами чисел абсолютно без какой-либо привязки к непрерывным функциям. К примеру у Вас вообще не существуют синусоидальные сигналы период которых не кратен шагу дискретизации. Вот нету их просто и всё. При этом Вы с чего-то решили что можете поучать других (!) о том что правильно и что не правильно делать. Шикарно. Давайте сворачивать на этом дискуссию.
0
Моя позиция здесь совершенно не причём.
Я лишь выражаю своё понимание ДПФ, сформировавшегося под влиянием некоторого количества литературы и собственных экспериментов, а также программирования функций для FFT и FHT.
Если в моём понимании есть неточности, то я только буду рад от них избавиться. ДПФ мне интересен как инструмент, а не средство самоутверждения.
ДПФ — это самостоятельный инструмент, и его вовсе не обязательно привязывать к непрерывному аналоговому сигналу. Как минимум потому, что существуют данные, дискретные по своей природе — например, последовательность бит. У ДПФ есть и менее очевидные приложения — например, умножение длинных чисел или подсчёт клеток в клеточном автомате.
Если бы ваша статья называлась "Спектральный анализ сигналов" — тогда этой дискуссии, возможно, и не было бы.
Я лишь выражаю своё понимание ДПФ, сформировавшегося под влиянием некоторого количества литературы и собственных экспериментов, а также программирования функций для FFT и FHT.
Если в моём понимании есть неточности, то я только буду рад от них избавиться. ДПФ мне интересен как инструмент, а не средство самоутверждения.
ДПФ — это самостоятельный инструмент, и его вовсе не обязательно привязывать к непрерывному аналоговому сигналу. Как минимум потому, что существуют данные, дискретные по своей природе — например, последовательность бит. У ДПФ есть и менее очевидные приложения — например, умножение длинных чисел или подсчёт клеток в клеточном автомате.
Если бы ваша статья называлась "Спектральный анализ сигналов" — тогда этой дискуссии, возможно, и не было бы.
0
Уважаемый товарищ Refridgerator, вы же в курсе того, я надеюсь, что большинство алгоритмов использующих FFT для быстрой свертки, включая алгоритм быстрого умножения используют «в корне неверное» (tm) дополнение нолями? Циклическое заворачивание свертки при ее реализации через ДПФ значительно чаще является недостатком чем достоинством. А так конечно да, ДПФ используется и как самостоятельный инструмент для обработки векторов чисел, я с этим и не спорю. И да, кое-где циклическая свертка может быть плюсом. Но я в статье рассказывал о семействе преобразований Фурье, включая непрерывные его варианты, а непрерывное к дискретному, так уж получилось, привязывается сугубо через дополнение нолями.
-1
Ваш пример скорее доказывает обратное.
Здесь дополнение нулями используется для резервирования места под результат, а не приближения спектра к непрерывному. И дополнение нулей сверх необходимого не даст ничего, кроме увеличения погрешности вычисления.
А по вопросу дискуссии есть и мнения со стороны:
Здесь дополнение нулями используется для резервирования места под результат, а не приближения спектра к непрерывному. И дополнение нулей сверх необходимого не даст ничего, кроме увеличения погрешности вычисления.
А по вопросу дискуссии есть и мнения со стороны:
But the DTFT is difficult to evaluate on a computer, since a computer works only on finite number of points. So to make the evaluation of the DTFT possible on a computer, we choose a finite number of frequency points.
Since the DFT is basically the sampled version of the DTFT, it is also periodic, with period N(the number of frequency samples taken).
0
Так мы о каком-либо спектре в данном случае вообще не говорим. DFT здесь используется чисто как некоторое преобразование над вектором чисел с некими интересными свойствами. И даже в этом случае оказывается удобным дополнять вектор нолями, причем не только для резервирования места, но и для подгонки длины под «удобные» для БПФ последовательности.
Вспомните с чего началась дискуссия.
>> Однако реальные доступные нам сигналы всегда имеют конечную длину — что делать? Для решения этой проблемы в FT и DTFT конечный сигнал просто дополняют слева и справа на бесконечность нулями.
> Это в корне неверно.
Я Вам уже разобрал случай когда ДПФ используется для оценки спектра непрерывного сигнала. Я показал что там при дополнении нолями там получается правильный результат с хорошей точностью и остающаяся «неидеальность» связана с «аналоговой» частью проблемы в виде доступной длительности сигнала. Я опроверг Ваше неверное утверждение о том что якобы при дополнении нолями обратное ДПФ не позволит восстановить исходную последовательность. Сейчас мы дошли до вариантов использования ДПФ где о спектре вообще говорить бессмысленно — но даже там широко применяется дополнение нолями. И вот я все пытаюсь понять почему же несмотря на все вышеприведенные примеры использования дополнения нолями как для практических вычислений так и с точки зрения общей теории делать это, с позиций Вашего опыта, «в корне неправильно»?
Да, я в курсе что ДПФ можно трактовать как некий специальный случай ПФ для периодических функций особого вида. Да я в курсе что есть люди которые считают что это единственная возможная трактовка, причем не для реального случая (функций на окружности) а для функций заданных на R. Нет, это не делает их точку зрения правильной. Вон выше в комментариях Вы можете найти ссылки на серьезные книжки, авторы которых на полном серьезе считают что на выходе ЦАП будет «ступенчатый» сигнал. Причем я же ведь даже не против подобного определения ДПФ, оно как я уже писал в некоторых аспектах удобнее, просто Вы же его распространяете на ситуацию где это определение уже не применимо и из него неверные выводы делаете относительно дополнения нолями.
Вспомните с чего началась дискуссия.
>> Однако реальные доступные нам сигналы всегда имеют конечную длину — что делать? Для решения этой проблемы в FT и DTFT конечный сигнал просто дополняют слева и справа на бесконечность нулями.
> Это в корне неверно.
Я Вам уже разобрал случай когда ДПФ используется для оценки спектра непрерывного сигнала. Я показал что там при дополнении нолями там получается правильный результат с хорошей точностью и остающаяся «неидеальность» связана с «аналоговой» частью проблемы в виде доступной длительности сигнала. Я опроверг Ваше неверное утверждение о том что якобы при дополнении нолями обратное ДПФ не позволит восстановить исходную последовательность. Сейчас мы дошли до вариантов использования ДПФ где о спектре вообще говорить бессмысленно — но даже там широко применяется дополнение нолями. И вот я все пытаюсь понять почему же несмотря на все вышеприведенные примеры использования дополнения нолями как для практических вычислений так и с точки зрения общей теории делать это, с позиций Вашего опыта, «в корне неправильно»?
Да, я в курсе что ДПФ можно трактовать как некий специальный случай ПФ для периодических функций особого вида. Да я в курсе что есть люди которые считают что это единственная возможная трактовка, причем не для реального случая (функций на окружности) а для функций заданных на R. Нет, это не делает их точку зрения правильной. Вон выше в комментариях Вы можете найти ссылки на серьезные книжки, авторы которых на полном серьезе считают что на выходе ЦАП будет «ступенчатый» сигнал. Причем я же ведь даже не против подобного определения ДПФ, оно как я уже писал в некоторых аспектах удобнее, просто Вы же его распространяете на ситуацию где это определение уже не применимо и из него неверные выводы делаете относительно дополнения нолями.
0
небольшое лирическое отступление, не имеющие никакого отношения к вопросу дискуссии
Уже сам факт наличия этой чрезмерно затянувшейся дискуссии говорит о том, что присутствует непонимание с обоих сторон вне зависимости от того, кто прав, правы ли оба или же не прав никто.
Предположим, я неправ, а Вы — правы. Тогда бы Вы смогли сформулировать ответ таким образом, что мне (и сторонним наблюдателям) моё заблужение стало бы очевидным.
Предположим, я прав, а Вы — неправы. Тогда я выступаю в роли нападающего, который ставит под сомнение Вашу квалификацию, а вы вынуждены защищаться.
Предположим, мы оба правы. Тогда имеет место быть неточная подача материала, допускающая неоднозначную трактовку.
Предположим, я неправ, а Вы — правы. Тогда бы Вы смогли сформулировать ответ таким образом, что мне (и сторонним наблюдателям) моё заблужение стало бы очевидным.
Предположим, я прав, а Вы — неправы. Тогда я выступаю в роли нападающего, который ставит под сомнение Вашу квалификацию, а вы вынуждены защищаться.
Предположим, мы оба правы. Тогда имеет место быть неточная подача материала, допускающая неоднозначную трактовку.
Так мы о каком-либо спектре в данном случае вообще не говорим. DFT здесь используется чисто как некоторое преобразование над вектором чисел с некими интересными свойствами.Как это не говорим? Я получаю спектры сигнала, перемножаю их комплексно и делаю обратное преобразование, всё по науке.
По остальному. Я уже неоднократно подчёркивал, что все мои комментарии написаны в контексте конечного числа вычислений ДПФ. Дополнение нулями в бесконечность сделают это невозможным.
Я вовсе не отрицаю операцию дополнения нулями в бесконечность конечного сигнала. Я хотел сказать, что:
а) её не нужно привязывать к ДПФ по-умолчанию,
б) её не нужно рассматривать саму по себе, вне контекста задачи,
в) для гармонического анализа части известного сигнала (как конечного, так и бесконечного) дополнение нулями — не единственная и не самая лучшая операция.
Если мы к конечному сигналу применяем FIR-фильтр, то размер сигнала увеличивается на длину ядра-1.
Если мы к конечному сигналу применяем физически реализуемвй IIR-фильтр, то размер сигнала становится бесконечным в одну сторону.
Если же мы меняем спектр конечного сигнала произвольно, то он автоматически становится бесконечным в обе стороны.
В теории схемотехники удобнее манипулировать именно произвольными операциями над спектром, поэтому и требуется бесконечное дополнение. Но далеко не всё из теории реализуемо на практике в аналоговом исполнении — например, сдвиг фаз всех частот на 90°.
Нули здесь фигурируют только потому, что операции наши — интегральные, а сигнал или его часть рассматриваются самостоятельно, и играют роль «начальной инициализации». Если бы мы использовали мультипликативные операции, то у нас были бы уже не нули, а единицы.
Та же свёртка через БПФ производится не за один раз, а кусочно с перекрытием. И вот в месте перекрытия у нас происходит дополнение не нулями, а «хвостом» от предыдущей свёртки.
0
Мы возвращаемся к все тому же «спектру вектора чисел». На мой взгляд подобное определение в отрыве от контекста бессмысленно. Вы можете взять к примеру точку в 3D пространстве и посчитать ее «спектр». Или посчитать «спектр полинома». Подобный термин вполне может быть кратким сокращением для «результат применения ДПФ» (или другого аналогичного преобразования), но переносить на него ассоциации со спектром непрерывных функций — очень плохая идея.
Далее, я не очень понимаю к чему Вы несколько раз упоминаете про невычислимое продолжение нолями в бесконечность. Продолжение нолями в бесконечность (а точнее зануление сигнала вне некоторого отрезка) относится к аналоговому сигналу и позволяет рассчитать непрерывный спектр ПФ дискретного времени для аналогового сигнала конечной длины. ДПФ с продолжением нолями на любой конечный интервал — это просто способ посчитать равномерно распределенное дискретное подмножество точек из этого спектра.
А так-то я с Вами не спорил вроде нигде что не надо бездумно дописывать ноли ко входу ДПФ везде и всюду. Я согласен с пунктами а, б и тем что это не единственная операция для гармонического анализа. Я говорил лишь что
а) Это то что надо делать для сигналов конечной длительности
б) Это позволяет эффективно посчитать через БПФ сколь угодно точное приближение непрерывного спектра ПФ дискретного времени
в) Дополнение нолями вообще является типовой операцией для БПФ (она вообще говоря вроде возникает везде где нет явной и точно известной периодичности в исходных данных)
Далее, я не очень понимаю к чему Вы несколько раз упоминаете про невычислимое продолжение нолями в бесконечность. Продолжение нолями в бесконечность (а точнее зануление сигнала вне некоторого отрезка) относится к аналоговому сигналу и позволяет рассчитать непрерывный спектр ПФ дискретного времени для аналогового сигнала конечной длины. ДПФ с продолжением нолями на любой конечный интервал — это просто способ посчитать равномерно распределенное дискретное подмножество точек из этого спектра.
А так-то я с Вами не спорил вроде нигде что не надо бездумно дописывать ноли ко входу ДПФ везде и всюду. Я согласен с пунктами а, б и тем что это не единственная операция для гармонического анализа. Я говорил лишь что
а) Это то что надо делать для сигналов конечной длительности
б) Это позволяет эффективно посчитать через БПФ сколь угодно точное приближение непрерывного спектра ПФ дискретного времени
в) Дополнение нолями вообще является типовой операцией для БПФ (она вообще говоря вроде возникает везде где нет явной и точно известной периодичности в исходных данных)
+1
4.2. Если ставить вопрос как «можно ли аппроксимировать дискретный спектр непрерывным таким образом, чтобы при обратном ПФ получить дополнение нулями» — то да, можно.
0
Вы зря зацикливаетесь на «дискретном спектре». Спектр дискретной функции как правило является непрерывным. Дискретные спектры характерны только для периодических функций, составляющих в определенном смысле «меньшинство» среди всех возможных.
0
Спектр дискретной функции дискретный по определению.
С тем же успехом вы могли бы сказать, например, применительно к теореме Ферма:
«Вы зря зацикливаетесь на натуральных числах. Натуральные числа, как правило, действительные»
С тем же успехом вы могли бы сказать, например, применительно к теореме Ферма:
«Вы зря зацикливаетесь на натуральных числах. Натуральные числа, как правило, действительные»
0
Не вижу по вашей ссылке подтверждения ваших слов.
0
0
А Вы свои ссылки, простите, читаете?
The discrete-time Fourier transform, on the other hand, maps functions with discrete time (discrete-time signals) to functions that have a continuous frequency domain
The discrete-time Fourier transform, on the other hand, maps functions with discrete time (discrete-time signals) to functions that have a continuous frequency domain
0
Конечно, читаю.
Там-то речь о ДПФ на бесконечном промежутке времени.
А тут мы с самого начала говорим об ограниченном во времени сигнале.
Наш исходный дискретный сигнал ограничен частотами от 0 до f.
Чем больше значений мы берём для ДПФ, тем больше у нас дискретных значений между 0 и f, и соответственно, тем меньше расстояние между ними. Следовательно в пределе получаем непрерывность.
Там-то речь о ДПФ на бесконечном промежутке времени.
А тут мы с самого начала говорим об ограниченном во времени сигнале.
Наш исходный дискретный сигнал ограничен частотами от 0 до f.
Чем больше значений мы берём для ДПФ, тем больше у нас дискретных значений между 0 и f, и соответственно, тем меньше расстояние между ними. Следовательно в пределе получаем непрерывность.
0
Нет. В данном треде речь шла просто о «дискретном сигнале». К примеру последовательности данных идущих с выхода АЦП на вход которого поступает аналоговый синус. Как именно эту последовательность обрезать для обработки — решаем мы сами. Это не некое божественное откровение данное сверху, это наша собственная аппроксимация которую мы делаем чтобы ограничить время захвата данных и объем вычислений. Вы просто тупо берете от балды некоторый вектор чисел, берете от него ДПФ и объявляете получившийся результат «спектром». А спектром чего? Спектром выбранного вами вектора чисел, надо полагать, потому что ни со спектром сигнала идущего с выхода АЦП ни тем более спектром исходного аналогового сигнала он не является. Ну и дальше занимаетесь религиозным поучением того что исходный вектор чисел нельзя дополнять нолями потому что это же даст другой спектр! Ну и что, говорите вы, что он будет иметь со спектром исходного аналогового сигнала намного больше общего? Это другой спектр и точка.
Хватит на этом. Закончили.
Хватит на этом. Закончили.
0
И как же так получается что «некорректное и бессмысленное» дополнение нолями дает правильный ответ причем очень простым и удобным способом не требующим никакой интерполяции или свертки?Своим дополнением нулями (по сути — умножением на прямоугольное окно) вы как раз и сделали эту свёртку.
0
Это можно было бы сделать и наоборот — сначала прямое БПФ, вставить нули, сделать обратное БПФ, умножить на прямоугольное окно.
0
Верно. Но я Вас спрашивал почему ответ получился при этом правильным :)? И я, надеюсь, Вы не будете спорить что дописывание нолей перед FFT — операция на порядок более простая чем попытки делать свертку самому?
0
Я, если честно, не увидел у вас правильного ответа. На графике — 5, макс. значение = 14.5, хотя в оригинальном сигнале амплитуда была равна единице.
0
Если Вы посмотрите код, то убедитесь что я не заморачивался с нормировкой. Если хочется считать амплитуду то предварительно надо взять DFT с той же нормировкой от функции окна, взять нулевой коэффициент и поделить его на два (из-за симметричности спектра любой синус по амплитуде раскладывается пополам на частоты +f и -f). Для прямоугольного окна длины N и дефолтной нормировки используемой numpy.fft соответствующий нормализующий коэффициент равен N/2, т.е. в данном конкретном примере 5. Отсюда
Freq 1= 14.453125 amplitude= 0.994229918421
Это естественно не идеальные 15.32 и 1.00 в силу конечности отрезка измерения (0.01 сек), но довольно близко к ним.
Freq 1= 14.453125 amplitude= 0.994229918421
Это естественно не идеальные 15.32 и 1.00 в силу конечности отрезка измерения (0.01 сек), но довольно близко к ним.
0
Любая конечная сумма синусов и косинусов бесконечна и периодичнаВот вам пример:
sin(x)+sin(x*sqrt(2))
Бесконечна, но не периодична
0
Да, знаю, неудачно выразился. Имелась в виду разумеется «сумма синусов и косинусов того вида который используется в ПФ», т.е. с частотами кратными целым числам.
0
Вернёмся к вашему примеру.
Имеем 10 точек синусоиды 15.34 Гц с частотой дискретизации 100 Гц (фиолетовый), они же, дополненные нулями до 1024 (красный), и для сравнения, та же синусоида, но 1024 точки (синий):

Видно, что максимум сигнала с дополненными нулями находится достаточно близко к оригинальной частоте.
А теперь возьмём и добавим ещё одну синусоиду с частотой 24.99 Гц:

Видно, что максимум сместился от первоначального положения.
А теперь добавим ещё больше нулей, до 8192:

Видно, что на точность это никак не повлияло.
А теперь самое интересное.
И в первом, и во втором случае мы имеем 5 локальных максимумов. Как отличить, являются эти максимумы лепестками или же реальными частотными составляющими?
Имеем 10 точек синусоиды 15.34 Гц с частотой дискретизации 100 Гц (фиолетовый), они же, дополненные нулями до 1024 (красный), и для сравнения, та же синусоида, но 1024 точки (синий):

Видно, что максимум сигнала с дополненными нулями находится достаточно близко к оригинальной частоте.
А теперь возьмём и добавим ещё одну синусоиду с частотой 24.99 Гц:

Видно, что максимум сместился от первоначального положения.
А теперь добавим ещё больше нулей, до 8192:

Видно, что на точность это никак не повлияло.
А теперь самое интересное.
И в первом, и во втором случае мы имеем 5 локальных максимумов. Как отличить, являются эти максимумы лепестками или же реальными частотными составляющими?
0
И в первом, и во втором случае мы имеем 5 локальных максимумов. Как отличить, являются эти максимумы лепестками или же реальными частотными составляющими?
Ну, конкретно в Вашем примере разница в 10 дБ между основными пиками и побочными довольно прозрачно намекает какие пики основные :). Но можно для контроля использовать оконные функции у которых сильно подавлены боковые лепестки. К примеру банально домножить исходную последовательность на окно Ханна

Для настолько короткой последовательности основные лепестки получаются как Вы можете видеть очень широкими и для нашей пары частот они сливаются, мешая точно определить частоту, амплитуду и фазу сигнала. Но для подсчета количества реально существующих синусоид — самое оно. Побочные лепестки настолько малы что основной сигнал с ними перепутать невозможно.
В общем же случае подобная задача не всегда имеет решение. Для разделения сигналов с близкими частотами или сигналов с сильно разными амплитудами или если в спектре много синусоид длины сигнала может просто-напросто не хватить.
-1
Ну, я бы не назвал операцию умножения на окно «банальной».
В соответствии с всё той же теоремой о свёртке, умножение во временной области равносильно свёртке в частотной. А поскольку сворачиваются именно комплексные частоты, а не их модули (амплитуды), результат может довольно сильно отличаться от ожидаемого.
Возьмём к примеру вот такой сигнал длиной 500 семплов:
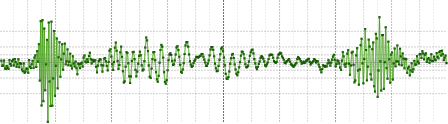
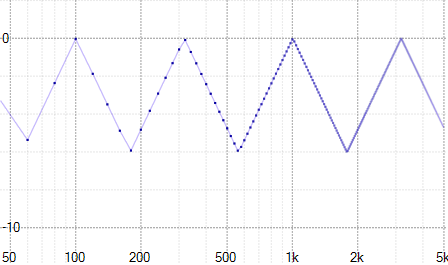
При умножении его на окно Ханна и дополнении нулями до 1024 получим следующее (красным):


Как видно, результирующая АЧХ весьма слабо напоминает оригинальную.
В соответствии с всё той же теоремой о свёртке, умножение во временной области равносильно свёртке в частотной. А поскольку сворачиваются именно комплексные частоты, а не их модули (амплитуды), результат может довольно сильно отличаться от ожидаемого.
Возьмём к примеру вот такой сигнал длиной 500 семплов:


При умножении его на окно Ханна и дополнении нулями до 1024 получим следующее (красным):


Как видно, результирующая АЧХ весьма слабо напоминает оригинальную.
0
Прошу прощения, но о какой оригинальной АЧХ идет речь? Вы снова о «спектре последовательности чисел», сиречь результате применения ДПФ к определенному вектору? Вы конечно правы что после применения «окна» он изменится, но для этого не надо было нового примера городить, это не только очевидно, но и было уже продемонстрировано в прошлом примере.
Если мы говорим о том что первая последовательность чисел была получена в результате оцифровки какого-то сигнала, то «оригинальную АЧХ» следовало бы мерять именно на этом исходном сигнале. А результат ДПФ «без применения» окна при этом окажется, как ни странно, сверткой этой исходной АЧХ со спектром окна. В полном соответствии с «теоремой о свертке» — ибо прямоугольное окно которое возникает при ограничении сигнала на любой конечный интервал тоже имеет свой собственный нетривиальный спектр. Судя по тому какой спектр у Вас изображен у первого сигнала, Вы об этом не задумывались и «сигнал» посчитали просто взяв обратное ДПФ от некоторой придуманной Вами функции. Я угадал?
Если мы говорим о том что первая последовательность чисел была получена в результате оцифровки какого-то сигнала, то «оригинальную АЧХ» следовало бы мерять именно на этом исходном сигнале. А результат ДПФ «без применения» окна при этом окажется, как ни странно, сверткой этой исходной АЧХ со спектром окна. В полном соответствии с «теоремой о свертке» — ибо прямоугольное окно которое возникает при ограничении сигнала на любой конечный интервал тоже имеет свой собственный нетривиальный спектр. Судя по тому какой спектр у Вас изображен у первого сигнала, Вы об этом не задумывались и «сигнал» посчитали просто взяв обратное ДПФ от некоторой придуманной Вами функции. Я угадал?
0
Добавлю картинку для наглядности:

Под словом «спектр» как видите можно понимать целых четыре разные вещи. На мой взгляд, обыкновенно когда речь заходит о спектре «сигнала», то под «эталонным» подразумевается спектр №1, а все остальные спектры являются приближением к нему. Чем длиннее доступный отрезок времени измерения, чем больше частота дискретизации, чем больше вычислительные ресурсы — тем точнее можно сделать это приближение.
Верны следующие утверждения
1. Спектр №2 является сверткой спектра №1 со спектром оконной функции (например прямоугольной, если мы просто берем какую-то подвыборку сигнала не домножая ее ни на чего)
2. Если окно достаточно длинное то спектр №2 является близким приближением спектра №1, и чем длиннее отрезок измерения — тем меньше разница
3. Если спектр исходного сигнала является «достаточно узкополосным», к пример не содержит частот выше половины частоты дискретизации и используется оконная функция которая тоже не имеет слишком высоких частот, то спектр дискретизованного сигнала является близким приближением к спектру №2.
4. Для вычисления сколь угодно точного приближения этого спектра нужно дополнить спектр «достаточно большим» числом нолей — т.е. спектр после дискретизации — это спектр №4
5. Вычисление ДПФ на более короткой последовательности (без дополнения нолями вообще или с коротким дополнением нолями) дает спектр №3 который является подмножеством спектра №4.
Таким образом мы можем посчитать сколь угодно точно спектр №4 и если частота дискретизации достаточна, то этот спектр почти не будет отличаться от спектра №2. А вот спектр №1 по спектру №2 восстановить, к сожалению, однозначно невозможно — как Вы верно заметили, мы не можем однозначно судить о произвольном сигнале по его конечному отрезку. Но мы знаем что спектр №2 — это результат свертки №1 с спектром «оконной функции» и, что приятно, можем в определенных пределах эту оконную функцию изменять. Благодаря этому мы можем выбрать оконную функцию которая хорошо сохраняет интересующие нас свойства спектра №1 и определить то что нас интересует из спектра №2.
Ваша же позиция, насколько я могу судить, сводится к тому чтобы объявить спектром сигнала спектр №3 и указать мне на то что он может изменяться в зависимости от, скажем, выбранной оконной функции. Ну так да, он может конечно изменяться. Только он, простите, будет меняться и при изменении отрезка измерения (как при изменении длины отрезка так и при его сдвиге), и при изменении частоты дискретизации. Вы уверены что Вы хотите ввести определение спектра сигнала именно подобным образом?

Под словом «спектр» как видите можно понимать целых четыре разные вещи. На мой взгляд, обыкновенно когда речь заходит о спектре «сигнала», то под «эталонным» подразумевается спектр №1, а все остальные спектры являются приближением к нему. Чем длиннее доступный отрезок времени измерения, чем больше частота дискретизации, чем больше вычислительные ресурсы — тем точнее можно сделать это приближение.
Верны следующие утверждения
1. Спектр №2 является сверткой спектра №1 со спектром оконной функции (например прямоугольной, если мы просто берем какую-то подвыборку сигнала не домножая ее ни на чего)
2. Если окно достаточно длинное то спектр №2 является близким приближением спектра №1, и чем длиннее отрезок измерения — тем меньше разница
3. Если спектр исходного сигнала является «достаточно узкополосным», к пример не содержит частот выше половины частоты дискретизации и используется оконная функция которая тоже не имеет слишком высоких частот, то спектр дискретизованного сигнала является близким приближением к спектру №2.
4. Для вычисления сколь угодно точного приближения этого спектра нужно дополнить спектр «достаточно большим» числом нолей — т.е. спектр после дискретизации — это спектр №4
5. Вычисление ДПФ на более короткой последовательности (без дополнения нолями вообще или с коротким дополнением нолями) дает спектр №3 который является подмножеством спектра №4.
Таким образом мы можем посчитать сколь угодно точно спектр №4 и если частота дискретизации достаточна, то этот спектр почти не будет отличаться от спектра №2. А вот спектр №1 по спектру №2 восстановить, к сожалению, однозначно невозможно — как Вы верно заметили, мы не можем однозначно судить о произвольном сигнале по его конечному отрезку. Но мы знаем что спектр №2 — это результат свертки №1 с спектром «оконной функции» и, что приятно, можем в определенных пределах эту оконную функцию изменять. Благодаря этому мы можем выбрать оконную функцию которая хорошо сохраняет интересующие нас свойства спектра №1 и определить то что нас интересует из спектра №2.
Ваша же позиция, насколько я могу судить, сводится к тому чтобы объявить спектром сигнала спектр №3 и указать мне на то что он может изменяться в зависимости от, скажем, выбранной оконной функции. Ну так да, он может конечно изменяться. Только он, простите, будет меняться и при изменении отрезка измерения (как при изменении длины отрезка так и при его сдвиге), и при изменении частоты дискретизации. Вы уверены что Вы хотите ввести определение спектра сигнала именно подобным образом?
+1
Я не ввожу никаких новых новых определений, а всего лишь использую готовые и устоявшиеся. Мне лично совершенно всё равно, говорить «спектр» или «frequency domain», однако «спектральный анализ» применительно к результату ДПФ используется повсеместно.
0
На вашей картинке в самом начале стоит «аналоговый сигнал». Однако преобразование Фурье — это чисто математическая операция, которая переводит time domain в frequency domain и к никаким сигналам по умолчанию не привязана.
0
Вот что например пишут про преобразование Фурье вот здесь:
В спектральном анализе исследуются периодические модели данных. Цель анализа — разложить комплексные временные ряды с циклическими компонентами на несколько основных синусоидальных функций с определенной длиной волн. Термин «спектральный» — своеобразная метафора для описания природы этого анализа. Предположим, вы изучаете луч белого солнечного света, который, на первый взгляд, кажется хаотически составленным из света с различными длинами волн. Однако, пропуская его через призму, вы можете отделить волны разной длины или периодов, которые составляют белый свет. Фактически, применяя этот метод, вы можете теперь распознавать и различать разные источники света. Таким образом, распознавая существенные основные периодические компоненты, вы узнали что-то об интересующем вас явлении. В сущности, применение спектрального анализа к временным рядам подобно пропусканию света через призму. В результате успешного анализа можно обнаружить всего несколько повторяющихся циклов различной длины в интересующих вас временных рядах, которые, на первый взгляд, выглядят как случайный шум.
Наиболее известный пример применения спектрального анализа — циклическая природа солнечных пятен (например, см. Блумфилд, 1976 или Шамвэй, 1988). Оказывается, что активность солнечных пятен имеет 11-ти летний цикл. Другие примеры небесных явлений, изменения погоды, колебания в товарных ценах, экономическая активность и т.д. также часто используются в литературе для демонстрации этого метода.
-1
Допустим, мы анализируем колебания цен на хлеб. Сегодня он стоит 20 р., вчера — 19р., а 30 лет назад — 20 коп. Однако не было момента сегодня ночью, когда он стоил 19.594р. Также как и много лет ранее не было момента, когда он стоил 0 р.
-1
Кажется, еще несколько дней назад прозвучало утверждение, что статья описывает ПФ как метод анализа аналоговых сигналов — а не как математический трюк общего назначения. Зачем вы продолжаете спорить?
0
ПФ работает и как математический метод анализа любых непрерывных R-или C-значных функций заданных на R^n. Но применительно к реальной жизни удобно использовать более понятный термин «аналоговый сигнал».
0
mayorovp, в последнее время мне уже несколько раз встречались комментарии в стиле «хабр уже не тот» потому что «никто не пишет комментарии по существу». Вот комментарии по существу, с ссылками и графиками, а не саркастическими тегами и мёртвыми котятами. Обсуждается тема, традиционно сложная для понимания. Рассмотрение её с диаметрально противоположных сторон оставляет возможность для дискуссии. Возможно, случайный Читатель сможет почерпнуть из этих комментариев (не только моих) чуть больше, чем из основной статьи.
0
Для меня остался непонятным вот такой момент.
Преобразование Фурье определено в поле комплексных чисел. Какие сигналы имеют комплексную природу? Для каких комплексных данных оно используется на практике? (Аналитический сигнал не считается, поскольку он изначально является искусственным).
Преобразование Фурье определено в поле комплексных чисел. Какие сигналы имеют комплексную природу? Для каких комплексных данных оно используется на практике? (Аналитический сигнал не считается, поскольку он изначально является искусственным).
0
Я у себя на домашней страничке написал про это преобразование Фурье, про ряды Фурье, про дискретное преобразование Фурье —
https://sites.google.com/site/burlachenkok/articles/faq_ft
https://sites.google.com/site/burlachenkok/articles/ft_advanced
https://sites.google.com/site/burlachenkok/articles/fourier-transform-and-dft-properties
Если это может быть интересно — читайте. Если есть конструктивные замечания — пишите.
https://sites.google.com/site/burlachenkok/articles/faq_ft
https://sites.google.com/site/burlachenkok/articles/ft_advanced
https://sites.google.com/site/burlachenkok/articles/fourier-transform-and-dft-properties
Если это может быть интересно — читайте. Если есть конструктивные замечания — пишите.
+1
Прочитал первую часть с большим удовольствием, написано отлично, читается легко и отличается точными и глубокими формулировками. Все очень здорово описано для результатов которых можно получить для «обычных», «школьных» функций. Примерно соответствует по духу и объему изложению теории на мехмате МГУ — Вы случайно не там учились :)? Из поправок — интеграл все-таки Римана («интеграла Римону») и мало кто из читателей знает что подразумевается в виду :).
Однако часть посвященная непрерывному ПФ выглядит достаточно слабой. ИМХО все же любое рассмотрение ПФ без хотя бы базового понимания обобщенных функций является неполноценным. При этом в контексте ПФ у обобщенных функций есть очень простое объяснение: это «распределения» значений (как «распределения в теории вероятности»). Интересно кстати что буржуи используют в этой области математики именно термин «distribution», а у нас это почему-то не прижилось.
Что такое распределение? Это очень часто встречающаяся концепция в физике. Допустим что у нас есть к примеру такая штука как равномерно заряженная проводящая сфера радиусом 1 метр содержащая заряд 1 кулон. Штука довольно интуитивно понятная: вне сферы заряда нет, а на сфере он распределен равномерно по её поверхности. Но как её можно описать математически? Мы не можем написать никакой функции вида q(x) которая бы возвращала бы нам заряд q для точки пространства x. Что делать? Математика дает на удивление простой ответ: а давайте будем брать не точки, а некоторые области пространства, например маленькие шарики радиусом 1 мм. Мы не можем вычислить «заряд сферы в точке», но мы можем вычислить заряд сферы оказавшийся заключенным в пределах любого выбранного нами шарика. А задав правило по которому мы можем посчитать заряд для любой заданной области мы тем самым определим нашу «заряженную сферу». То есть распределение — это более общая штука чем «обычная» функция (равномерно заряженную сферу обычной функцией не определишь) и ее можно описать в виде «функции» q(w) принимающей на вход «область» w для которой нужно посчитать заряд. А как можно задать эту «область пространства w»? Теорвер здесь шустро уходит в область теорий мер на множествах, но вместо этого можно сказать что w можно задать тоже функцией, к примеру, равной единице внутри области и нулю вне её. То есть распределение можно в каком-то смысле описать как «функцию от функций», причем обладающей специальными свойствами: к примеру если у нас есть две непересекающиеся области, u и v то очевидно заряд q(u+v) = q(u) + q(v). Но что это могут быть за свойства? И здесь имеет смысл сделать шаг назад и посмотреть на «более простой» случай который можно задать в виде функции — к примеру, равномерно заряженный шар у которого можно написать функцию плотности заряда q(x). Зная эту плотность мы легко посчитаем «заряд в области»: q(u) = \int_u q(x) dx. А с учетом ранее введенного определения u через функцию, q(u) = \int R q(x) u(x) dx.
А дальше внезапно оказывается что если сделать маленький шажок вперед и перейти от задания «областей» в виде функций вида «0 или 1» к некоторым более общим классам «базовых функций» (иными словами не просто выбрать точки в пространстве, но и назначить каждой из них какой-то вес), то «распределение q» для случая «обычных функций» оказывается непрерывным линейным оператором на пространстве «базовых функций» и это определение тривиально обобщается и на случай «распределения заряда на сфере». То есть такая физическая концепция как «распределение» может быть описана как линейный оператор на пространстве «базовых функций» и при некотором аккуратном выборе этого базового пространства пространство подобных «распределений» получается хорошим и сильно похожими на привычные нам функции, но более общим. Там идет очень хардкорный матанализ и функциональный анализ чтобы определить какие линейные функционалы «хорошие» и складываются в цельную непротиворечивую теорию, а какие «не очень», особенно в части того как они себя ведут на бесконечности, но для интуитивного понимания понятия «распределений» углубляться в эти дебри не надо. Понятие распределения легко соотносится с целой кучей физических сущностей и имеет огромное значение для решения многих дифференциальных уравнений.
Ну и в общем, long story short, непрерывное преобразование Фурье оказывается естественным образом определено именно для «комплекснозначных распределений», а не обычных функций, примерно так же как многие привычные нам функции типа экспоненты более естественно определены для комплексных переменных. Применительно к «обычным» функциям на входе из этого следует всего два практических ограничения:
1) в качестве «распределения» подходят не все функции вообще, а только интегрируемые (не надо пихать на вход какую-нибудь экзотику типа разрывной всюду функции) и «медленно растущие» — любая ограниченная (по максимальному значению) функция или полиномиал подойдут, а вот экспоненту на вход ПФ пихать не стоит
2) распределение отличается от простой функции тем что две кусочно-непрерывные функции отличающиеся только в счетном множестве точек — это одно и то же распределение (Вы мельком касаетесь этой темы упоминая функциональное пространство L2: в нем определена функциональная норма и по определению считается что если ||x-y||2 = 0 то x==y, то есть элементы этого пространства — это классы эквивалентности на пространстве всех возможных функций).
А дальше можно рассказывать про свойства ПФ для распределений — там все очень красиво и изящно. И в числе этих результатов оказывается что дискретное ПФ можно рассматривать как частный случай этого непрерывного ПФ для распределений.
Однако часть посвященная непрерывному ПФ выглядит достаточно слабой. ИМХО все же любое рассмотрение ПФ без хотя бы базового понимания обобщенных функций является неполноценным. При этом в контексте ПФ у обобщенных функций есть очень простое объяснение: это «распределения» значений (как «распределения в теории вероятности»). Интересно кстати что буржуи используют в этой области математики именно термин «distribution», а у нас это почему-то не прижилось.
Что такое распределение? Это очень часто встречающаяся концепция в физике. Допустим что у нас есть к примеру такая штука как равномерно заряженная проводящая сфера радиусом 1 метр содержащая заряд 1 кулон. Штука довольно интуитивно понятная: вне сферы заряда нет, а на сфере он распределен равномерно по её поверхности. Но как её можно описать математически? Мы не можем написать никакой функции вида q(x) которая бы возвращала бы нам заряд q для точки пространства x. Что делать? Математика дает на удивление простой ответ: а давайте будем брать не точки, а некоторые области пространства, например маленькие шарики радиусом 1 мм. Мы не можем вычислить «заряд сферы в точке», но мы можем вычислить заряд сферы оказавшийся заключенным в пределах любого выбранного нами шарика. А задав правило по которому мы можем посчитать заряд для любой заданной области мы тем самым определим нашу «заряженную сферу». То есть распределение — это более общая штука чем «обычная» функция (равномерно заряженную сферу обычной функцией не определишь) и ее можно описать в виде «функции» q(w) принимающей на вход «область» w для которой нужно посчитать заряд. А как можно задать эту «область пространства w»? Теорвер здесь шустро уходит в область теорий мер на множествах, но вместо этого можно сказать что w можно задать тоже функцией, к примеру, равной единице внутри области и нулю вне её. То есть распределение можно в каком-то смысле описать как «функцию от функций», причем обладающей специальными свойствами: к примеру если у нас есть две непересекающиеся области, u и v то очевидно заряд q(u+v) = q(u) + q(v). Но что это могут быть за свойства? И здесь имеет смысл сделать шаг назад и посмотреть на «более простой» случай который можно задать в виде функции — к примеру, равномерно заряженный шар у которого можно написать функцию плотности заряда q(x). Зная эту плотность мы легко посчитаем «заряд в области»: q(u) = \int_u q(x) dx. А с учетом ранее введенного определения u через функцию, q(u) = \int R q(x) u(x) dx.
А дальше внезапно оказывается что если сделать маленький шажок вперед и перейти от задания «областей» в виде функций вида «0 или 1» к некоторым более общим классам «базовых функций» (иными словами не просто выбрать точки в пространстве, но и назначить каждой из них какой-то вес), то «распределение q» для случая «обычных функций» оказывается непрерывным линейным оператором на пространстве «базовых функций» и это определение тривиально обобщается и на случай «распределения заряда на сфере». То есть такая физическая концепция как «распределение» может быть описана как линейный оператор на пространстве «базовых функций» и при некотором аккуратном выборе этого базового пространства пространство подобных «распределений» получается хорошим и сильно похожими на привычные нам функции, но более общим. Там идет очень хардкорный матанализ и функциональный анализ чтобы определить какие линейные функционалы «хорошие» и складываются в цельную непротиворечивую теорию, а какие «не очень», особенно в части того как они себя ведут на бесконечности, но для интуитивного понимания понятия «распределений» углубляться в эти дебри не надо. Понятие распределения легко соотносится с целой кучей физических сущностей и имеет огромное значение для решения многих дифференциальных уравнений.
Ну и в общем, long story short, непрерывное преобразование Фурье оказывается естественным образом определено именно для «комплекснозначных распределений», а не обычных функций, примерно так же как многие привычные нам функции типа экспоненты более естественно определены для комплексных переменных. Применительно к «обычным» функциям на входе из этого следует всего два практических ограничения:
1) в качестве «распределения» подходят не все функции вообще, а только интегрируемые (не надо пихать на вход какую-нибудь экзотику типа разрывной всюду функции) и «медленно растущие» — любая ограниченная (по максимальному значению) функция или полиномиал подойдут, а вот экспоненту на вход ПФ пихать не стоит
2) распределение отличается от простой функции тем что две кусочно-непрерывные функции отличающиеся только в счетном множестве точек — это одно и то же распределение (Вы мельком касаетесь этой темы упоминая функциональное пространство L2: в нем определена функциональная норма и по определению считается что если ||x-y||2 = 0 то x==y, то есть элементы этого пространства — это классы эквивалентности на пространстве всех возможных функций).
А дальше можно рассказывать про свойства ПФ для распределений — там все очень красиво и изящно. И в числе этих результатов оказывается что дискретное ПФ можно рассматривать как частный случай этого непрерывного ПФ для распределений.
0
Спасибо большое за комментарии по улучшению, и спасибо за доп. пояснения. Если будут ещё — пишите)
Я учился в МГТУ Баумана, но знания по этой теме получили из курса в Стенфорде от проф. Бреда Осгуда (Вот этот «весельчак» https://www.facebook.com/permalink.php?story_fbid=141679662888108&id=100011382256381)
Про распределение у меня в небольшом очерке есть здесь — https://sites.google.com/site/burlachenkok/articles/ft_advanced p.7.
Я разделил на кусочки статью — для всех (part I). Я лишь изредка касался вопросов про классы функций как в (Q10). Про распределения есть в https://sites.google.com/site/burlachenkok/articles/ft_advanced p.7
Я учился в МГТУ Баумана, но знания по этой теме получили из курса в Стенфорде от проф. Бреда Осгуда (Вот этот «весельчак» https://www.facebook.com/permalink.php?story_fbid=141679662888108&id=100011382256381)
Про распределение у меня в небольшом очерке есть здесь — https://sites.google.com/site/burlachenkok/articles/ft_advanced p.7.
Я разделил на кусочки статью — для всех (part I). Я лишь изредка касался вопросов про классы функций как в (Q10). Про распределения есть в https://sites.google.com/site/burlachenkok/articles/ft_advanced p.7
0
Я работаю в NVIDIA программистом, и у нас есть такой бонус с курсами в Стенфорде. В Гугле есть тоже похожая штука.
http://scpd.stanford.edu/nvidia/index.php
http://scpd.stanford.edu/google/index.php
http://scpd.stanford.edu/nvidia/index.php
http://scpd.stanford.edu/google/index.php
0
Я решил разобраться с этой штукой потому что было «вдохновение» Разобраться. В своём родном университете я учился на программиста и там не очень уделяли внимание функциональным преобразованиям (как преобразование Лапаса, и преобразование Фурье) для студентов по крайней мере моей кафедры (ИУ-7)
p.s. Я не знал, что на Хабре есть ограничение по времени на редактирование комментария. Хвост комментариев вышел.
p.s. Я не знал, что на Хабре есть ограничение по времени на редактирование комментария. Хвост комментариев вышел.
0
Из прочих замечаний по первой части:
1. Вы не упоминаете такую важную штуку как «преобразование Фурье дискретного времени» хотя она имеет важное значение для крайне важной теоремы Котельникова-Найквиста-Шеннона и представляет естественную связь между рядом Фурье, непрерывным преобразованием Фурье и дискретным преобразованием Фурье
2. Вы переходите сразу к «быстрому преобразованию Фурье» не объяснив вначале что такое «дискретное преобразование Фурье» :)
3. Упомянутый в «отличиях преобразований Фурье» множитель 1/N относится к т.н. «нормировке преобразования Фурье». Существует более одного определения что такое ПФ, отличающиеся только множителем (нормировочным коэффициентом). Тот что дает 1/N просто дает чуть более короткие формулы и удобен для программной реализации БПФ, но не надо это подавать как «принципиальное отличие», это просто элемент выбранной частной реализации (которую, впрочем, требуется учитывать если хочется из спектра ПФ оценить амплитуду или мощность исходного сигнала).
4. Пункты 14.1-14.2: там нет ничего странного и никаких «нестыковок физики с математикой». Само определение спектра дается через ПФ, понятия «ограниченного» и «неограниченного» спектра не имеют в связи с этим самостоятельного физического смысла. Однако есть довольно интересный частный момент связанный с «линейными частотными фильтрами». Бывают «фильтры с конечным временем отклика» (FIR) и «фильтры с бесконечным» (IIR): ну так вот, из 14.2 следует что любой FIR не может полностью отрезать высокие частоты. Но на практике это не ощутимо, «отклик на бесконечности» всегда стремится к нулю и может быть фантастически слабым, это будет формально математически не ноль, но полный ноль для любых практических целей.
5. Ш-функцию обычно называют «гребенкой Дирака»
1. Вы не упоминаете такую важную штуку как «преобразование Фурье дискретного времени» хотя она имеет важное значение для крайне важной теоремы Котельникова-Найквиста-Шеннона и представляет естественную связь между рядом Фурье, непрерывным преобразованием Фурье и дискретным преобразованием Фурье
2. Вы переходите сразу к «быстрому преобразованию Фурье» не объяснив вначале что такое «дискретное преобразование Фурье» :)
3. Упомянутый в «отличиях преобразований Фурье» множитель 1/N относится к т.н. «нормировке преобразования Фурье». Существует более одного определения что такое ПФ, отличающиеся только множителем (нормировочным коэффициентом). Тот что дает 1/N просто дает чуть более короткие формулы и удобен для программной реализации БПФ, но не надо это подавать как «принципиальное отличие», это просто элемент выбранной частной реализации (которую, впрочем, требуется учитывать если хочется из спектра ПФ оценить амплитуду или мощность исходного сигнала).
4. Пункты 14.1-14.2: там нет ничего странного и никаких «нестыковок физики с математикой». Само определение спектра дается через ПФ, понятия «ограниченного» и «неограниченного» спектра не имеют в связи с этим самостоятельного физического смысла. Однако есть довольно интересный частный момент связанный с «линейными частотными фильтрами». Бывают «фильтры с конечным временем отклика» (FIR) и «фильтры с бесконечным» (IIR): ну так вот, из 14.2 следует что любой FIR не может полностью отрезать высокие частоты. Но на практике это не ощутимо, «отклик на бесконечности» всегда стремится к нулю и может быть фантастически слабым, это будет формально математически не ноль, но полный ноль для любых практических целей.
5. Ш-функцию обычно называют «гребенкой Дирака»
+1
Отличная статья, добавил в закладки, но на внешней ссылке «свертка функций» я и застрял, так как нифига там не понял.
0
Вот спасибо за статью!
0
Понимаю что год прошел, но все же…
Почему произведение сигнала и гребенки Дирака дает отсчеты функции? Ведь дельта не единица, а бесеонечность....
0
Представьте это как смену единицы измерения. В непрерывном варианте у нас был уровень сигнала 12,34 в момент времени t, в дискретном стал 12,34δ (где δ — та самая "бесконечность").
Тут важнее тот факт, что все данные о сигнале между отсчетами необратимо пропали.
0
У меня проблема с тем что есть переход от поточенного перемножения функций к их свертке после преобразования. И все замечательно, но только к сожалению первоначальная функция умноженная на бесконечность не дает отсчеты начальной функции :(. Если бы там где-то был бы интеграл, то было бы применено фильтрующее свойство, а так я что-то не понимаю как :(
0
Если это для вас сложно, подойдите к задаче с другой стороны. Нарисуйте график дискретных отсчетов функции, после чего разделите его на исходную функцию. У вас получится вот такая функция:
f(x) = 1 для x = kT
f(x) = 0 для x != kT
Получилась функция, которая по построению при умножении на сигнал дает его отсчеты.
Но у нее есть проблема: ее образ Фурье — ноль, потому что мощность сигнала слишком мала. Поэтому ее нужно «умножить на бесконечность», т.е. свернуть с функцией Дирака — и получится как раз гребенка Дирака.
f(x) = 1 для x = kT
f(x) = 0 для x != kT
Получилась функция, которая по построению при умножении на сигнал дает его отсчеты.
Но у нее есть проблема: ее образ Фурье — ноль, потому что мощность сигнала слишком мала. Поэтому ее нужно «умножить на бесконечность», т.е. свернуть с функцией Дирака — и получится как раз гребенка Дирака.
+2
что значит сложно? Это просто математически неверно :).
Автор утверждает что функцию умножить на гребенку дирака — получаем оцифрованную функцию, дальше он это переводит в фурье образы, перемножает и получает повторение спектра.
Если повторить рассуждения автора, но с вашей функцией
f(x) = 1 для x = kT
f(x) = 0 для x != kT
то слева у нас точно оцифровка, а справа получается свертка нуля и спектра функции, то есть ноль. И вся теория рушится…
Однако если собраться и принять что оцифровка — это свертка гребня дирака и исходной функции. То слева все получается, за счет фильтрующего свойства дельта функций мы получаем семплинг. Теперь осталось понять что у нас справа.
Или я где то не прав?
Автор утверждает что функцию умножить на гребенку дирака — получаем оцифрованную функцию, дальше он это переводит в фурье образы, перемножает и получает повторение спектра.
Если повторить рассуждения автора, но с вашей функцией
f(x) = 1 для x = kT
f(x) = 0 для x != kT
то слева у нас точно оцифровка, а справа получается свертка нуля и спектра функции, то есть ноль. И вся теория рушится…
Однако если собраться и принять что оцифровка — это свертка гребня дирака и исходной функции. То слева все получается, за счет фильтрующего свойства дельта функций мы получаем семплинг. Теперь осталось понять что у нас справа.
Или я где то не прав?
0
Ну, тут требуется знание функционального анализа. А с его точки зрения говорить о «значении функции в точке» бессмысленно. Если мы рассматриваем пространство функций и пытаемся ввести там какую-то норму («меру расстояния» между двумя функциями), то для большинства интересных норм две «обычные» функции отличающиеся только значением в одной точке полностью равнозначны. И, скажем, описанная mayorovp «оцифрованная функция» тождественно равна нулю.
Возьмем теперь какую-нибудь функцию f. Заметим что можно выделить функции «хорошие» и «плохие». К примеру дифференцируемые функции — «хорошие», а какая-нибудь функция Дирихле — «плохая». Оказывается что для огромной массы построений, «хорошая» функция — это такая, что для любой компактной гладкой функции g можно посчитать интеграл по области определения от (fg). И в рамках этого определения получается что «функция» — это то что умеет ставить в соответствие функции (g) значение интеграла от (fg). Т.е. такая функция может рассматриваться как линейный функционал f(g) на пространстве компактных гладких функций. И вот это пространство линейных функционалов оказывается очень интересным и включающим в себя не только «обычные» функции но и те самые «обобщенные». Например дельта-функция Дирака — это линейный функционал ставящий в соответствие функции g значение g(0): delta(g)=g(0). Начинаете замечать «оцифровку»? Дельта-функция это не «бесконечность», это линейный функционал который ставит в соответствие функции ее значение в одной точке.
Откуда берется нотация бесконечности у дельта-функции? Попробуем дать определение «значения функции в точке» в смысле функционального анализа. Скажем для определенности — значение функции в точке 0. Берем последовательность гладких функций g_n заданных на все меньшем отрезке вокруг выбранной нами точке, скажем [-1/n,1/n] такую что интеграл от любой из g_n равен 1. Можно показать что для любой гладкой функции f, последовательность f(g_n) сходится к f(0). По сути мы вычисляем значение «в точке» беря интегралы от f по всей меньшей и меньшей окрестности вокруг выбранной точки и нормируя на площадь этой окрестности. Для дельта-функции как нетрудно заметить получим 0 во всех точках кроме 0, тогда как для 0 последовательность будет стремиться к бесконечности. Следовательно с позиции функана говорить о «значении дельта-функции в 0» бессмысленно
Ну и дальше оказывается что на этом вот интересном «пространстве линейных функционалов» можно естественным образом задать операции умножения на гладкую функцию, операции дифференцирования, интегрирования и преобразования Фурье. При этом окажется что в рамках этого определения интеграл от
dc(x)*f(x)e^(-2pi i x) где dc(x) — это гребенка Дирака,
будет просто суммой от
f(x)e^(-2pi i x) взятой в целочисленных точках
Поэтому в теории ПФ «оцифровкой» функции становится именно умножение на гребенку Дирака (ну, если быть точнее то в обратную сторону — умножение гребенки Дирака на функцию).
Возьмем теперь какую-нибудь функцию f. Заметим что можно выделить функции «хорошие» и «плохие». К примеру дифференцируемые функции — «хорошие», а какая-нибудь функция Дирихле — «плохая». Оказывается что для огромной массы построений, «хорошая» функция — это такая, что для любой компактной гладкой функции g можно посчитать интеграл по области определения от (fg). И в рамках этого определения получается что «функция» — это то что умеет ставить в соответствие функции (g) значение интеграла от (fg). Т.е. такая функция может рассматриваться как линейный функционал f(g) на пространстве компактных гладких функций. И вот это пространство линейных функционалов оказывается очень интересным и включающим в себя не только «обычные» функции но и те самые «обобщенные». Например дельта-функция Дирака — это линейный функционал ставящий в соответствие функции g значение g(0): delta(g)=g(0). Начинаете замечать «оцифровку»? Дельта-функция это не «бесконечность», это линейный функционал который ставит в соответствие функции ее значение в одной точке.
Откуда берется нотация бесконечности у дельта-функции? Попробуем дать определение «значения функции в точке» в смысле функционального анализа. Скажем для определенности — значение функции в точке 0. Берем последовательность гладких функций g_n заданных на все меньшем отрезке вокруг выбранной нами точке, скажем [-1/n,1/n] такую что интеграл от любой из g_n равен 1. Можно показать что для любой гладкой функции f, последовательность f(g_n) сходится к f(0). По сути мы вычисляем значение «в точке» беря интегралы от f по всей меньшей и меньшей окрестности вокруг выбранной точки и нормируя на площадь этой окрестности. Для дельта-функции как нетрудно заметить получим 0 во всех точках кроме 0, тогда как для 0 последовательность будет стремиться к бесконечности. Следовательно с позиции функана говорить о «значении дельта-функции в 0» бессмысленно
Ну и дальше оказывается что на этом вот интересном «пространстве линейных функционалов» можно естественным образом задать операции умножения на гладкую функцию, операции дифференцирования, интегрирования и преобразования Фурье. При этом окажется что в рамках этого определения интеграл от
dc(x)*f(x)e^(-2pi i x) где dc(x) — это гребенка Дирака,
будет просто суммой от
f(x)e^(-2pi i x) взятой в целочисленных точках
Поэтому в теории ПФ «оцифровкой» функции становится именно умножение на гребенку Дирака (ну, если быть точнее то в обратную сторону — умножение гребенки Дирака на функцию).
0
Так это же получается просто угловой спектр мощности?
Заголовок спойлера

0
Sign up to leave a comment.
Articles
Change theme settings
Простыми словами о преобразовании Фурье