«Я экспериментировал с задачами кубического представления в стиле предыдущей работы Эндрю и Ричарда Гая. Численные результаты были потрясающими…» (комментарий на MathOverflow)Вот так ушедший на покой математик Аллан Маклауд наткнулся на это уравнение несколько лет назад. И оно действительно очень интересно. Честно говоря, это одно из лучших диофантовых уравнений, которое я когда-либо видел, но видел я их не очень много.
Я нашёл его, когда оно начало распространяться как выцепляющая в сети нердов картинка-псевдомем, придуманная чьим-то безжалостным умом (Сридхар, это был ты?). Я не понял сразу, что это такое. Картинка выглядела так:

«95% людей не решат эту загадку. Сможете найти положительные целочисленные значения?»
Вы наверно уже видели похожие картинки-мемы. Это всегда чистейший мусор, кликбэйты: «95% выпускников МТИ не решат её!». «Она» — это какая-нибудь глупая или плохо сформулированная задачка, или же тривиальная разминка для мозга.
Но эта картинка совсем другая. Этот мем — умная или злобная шутка. Примерно у 99,999995% людей нет ни малейших шансов её решить, в том числе и у доброй части математиков из ведущих университетов, не занимающихся теорией чисел. Да, она решаема, но при этом по-настоящему сложна. (Кстати, её не придумал Сридхар, точнее, не он полностью. См. историю в этом комментарии).
Вы можете подумать, что если ничего другое не помогает, то можно просто заставить компьютер решать её. Очень просто написать компьютерную программу для поиска решений этого кажущегося простым уравнения. Разумеется, компьютер рано или поздно найдёт их, если они существуют. Большая ошибка. Здесь метод простого перебора компьютером будет бесполезен.
Не знаю, удастся ли уместить полное решение в статью, если не принять, что все уже знают всё необходимое об эллиптических кривых. Я могу привести здесь только краткий обзор. Основной справочный источник — это чудесная, относительно недавняя работа Бремнера и Маклауда под названием «An unusual cubic representation problem» («Необычная проблема кубического представления»), опубликованная в 2014 году в Annales Mathematicae et Informaticae.
Итак, приступим.
Мы ищем положительные целочисленные решения уравнения
(я заменил обозначения переменных теми, которые используются в работе).
Первое, что нужно сделать, исследуя любое уравнение — попробовать поместить его в нужный контекст. Надо задать вопрос: что это за уравнение? Так, нас просят найти целочисленные решения, то есть это задача теории чисел. В текущей формулировке в уравнении используются рациональные функции (многочлены, делящиеся на другие многочлены), но очевидно, что мы можем домножить на общее кратное знаменателей, чтобы подчистить уравнение и получить только многочлены, то есть привести его к виду диофантова уравнения. Требование «положительности» довольно необычно, и, как мы увидим, усложняет всё.
Итак, сколько же у нас тут переменных? Вопрос кажется глупым: очевидно, что три, а именно
Это значит, что уравнение только при��воряется трёхмерным. На самом деле оно двухмерно. В геометрическом представлении у нас есть поверхность (одно уравнение с тремя переменными в общем случае задаёт двухмерную поверхность. В целом,
Проще всего объянить это сведение можно так: мы можем разделить решения, какими бы они ни были, на те, при которых
Продолжим: какова степень нашего уравнения? Степень уравнения — это максимальная степень, любого появляющаяся в уравнении одночлена, где «одночлен» — это произведение нескольких переменных, чья «степень» является количеством перемножаемых одночленов. Например,
Поведение диофантовых уравнений сильно зависит от их степени. В целом:
- Со степенью
всё просто.
- Степень
полностью проанализирована и может быть решена довольно элементарными способами.
- Степень
— это обширный океан глубокой теории и миллион нерешённых проблем.
- Степень
и выше… Очень, очень сложны.
Мы имеем степень
Даже без раскрывания скобок можно увидеть, что степень равна
Вы можете возразить, что умножение на делители невозможно, если какие-то из них оказываются равны
На самом деле уравнение с многочленами легко решить, например,
Когда обнаруживаешь, что уравнение представляет собой эллиптическую кривую, то а) радуешься и б) отчаиваешься, потому что предстоит ещё много чего изучить. Это уравнение — прекрасный пример того, как мощную теорию эллиптических кривых можно применить к нахождению безумно сложно определяемых решений.
Первое, что обычно делают эллиптической кривой — приводят её в вейерштрассову форму. Это уравнение, которое выглядит как
а иногда как
(это называется развёрнутой вейерштрассовой формой. Она необязательна, но иногда более удобна).
Обычно любую эллиптическую кривую можно привести к такому виду (если вы только не работаете над полями с малыми характеристиками, но здесь нам не нужно о них волноваться). Объяснять способ поиска правильного преобразования было бы слишком долго, поэтому просто знайте, что это абсолютно механический процесс (критически важно в нём то, чтобы была хотя бы одна рациональная точка, которая у нас есть). Существуют разные пакеты вычислительной алгебры, которые сделают всё за вас.
Но даже если вы не знаете. как найти преобразование, проверить его очень просто, по крайней мере, это выполняется чисто механически. Необходимое преобразование в нашем случае задаётся страшно выглядящими формулами
Я знаю, что они похожи на неизвестно откуда взявшуюся магию вуду, но поверьте, это не так. Получив эти преобразования, с помощью монотонных, но довольно простых алгебраических расчётов мы покажем, что
Это уравнение, хоть и выглядит совсем по-другому, на самом деле является достоверной моделью исходного. Графически оно выглядит так — типичная эллиптическая кривая с двумя вещественными частями:
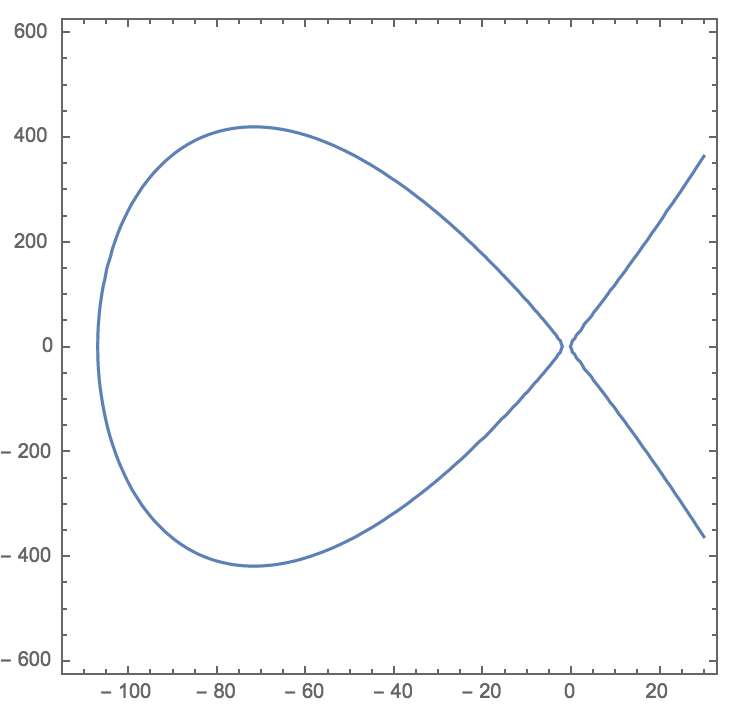
«Рыбий хвост» справа растёт «в бесконечность и дальше». Овальная фигура слева является замкнутой и оказывается для нас довольно интересной.
Имея любое решение
(Помните, что триплет
Два показанных нами отображения, из
Давайте рассмотрим пример.
На эллиптической кривой (2) есть хорошая рациональная точка:
И в самом деле,
как можно с лёгкостью убедиться. Это простое решение нашего исходного уравнения в целых числах, но, увы, не в положительных целых. Это решение непросто вывести вручную, но и несложно получить без всей этой рассматриваемой здесь махины, приложив немного терпения. Самая сложность заключается в положительных решениях.
Теперь, получив рациональную точку на эллиптической кривой, например,
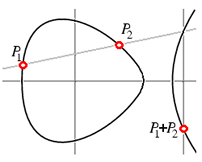
Для начала прибавим нашу точку
и снова эта новая точка соответствует значениям
Это решение определённо непросто найти вручную, но оно всё ещё под силу компьютеру. Однако оно по-прежнему неположительно.
Не пугаясь неудач, мы продолжаем вычислять
9P=(-66202368404229585264842409883878874707453676645038225/13514400292716288512070907945002943352692578000406921,
58800835157308083307376751727347181330085672850296730351871748713307988700611210/1571068668597978434556364707291896268838086945430031322196754390420280407346469)Его определённо непросто найти, но с помощью нашей машинерии нам достаточно повторить девять раз простую геометрическую процедуру. Соответствующие значения
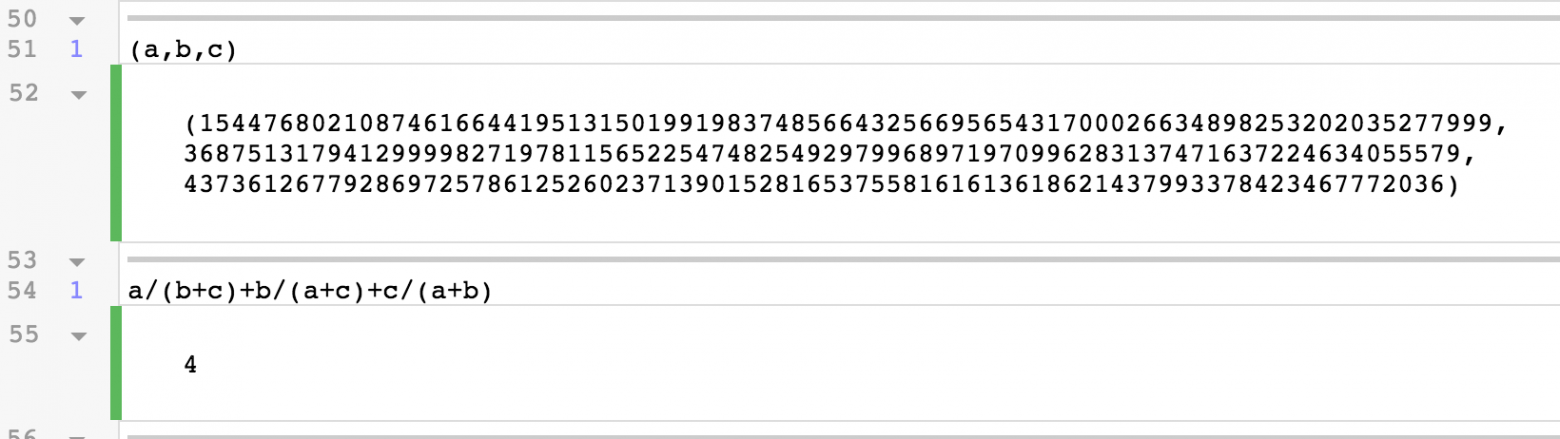
a=154476802108746166441951315019919837485664325669565431700026634898253202035277999,
b=36875131794129999827197811565225474825492979968971970996283137471637224634055579,
c=4373612677928697257861252602371390152816537558161613618621437993378423467772036Это 80-разрядные числа! Вы никак не смогли бы найти 80-разрядные числа на компьютере с помощью простого перебора. Выглядит невероятным, но вставив эти огромные числа в простое выражение
Фактически, они являются наименьшими решениями задачи. Если мы продолжим прибавлять к самой себе точку
Вернёмся к теории. Эллиптическая кривая над рациональными значениями имеет ранг, который является количеством точек, необходимых, чтобы использовать для метод хорд и касательных и быть уверенным, что мы рано или поздно найдём все рациональные точки на кривой. Наша эллиптическая кривая (2) имеет ранг 1. Это значит, что у неё есть бесконечное количество рациональных точек, но все они получаются из единственной, которая является ничем иным, как нашей точкой
В нашем случае точка
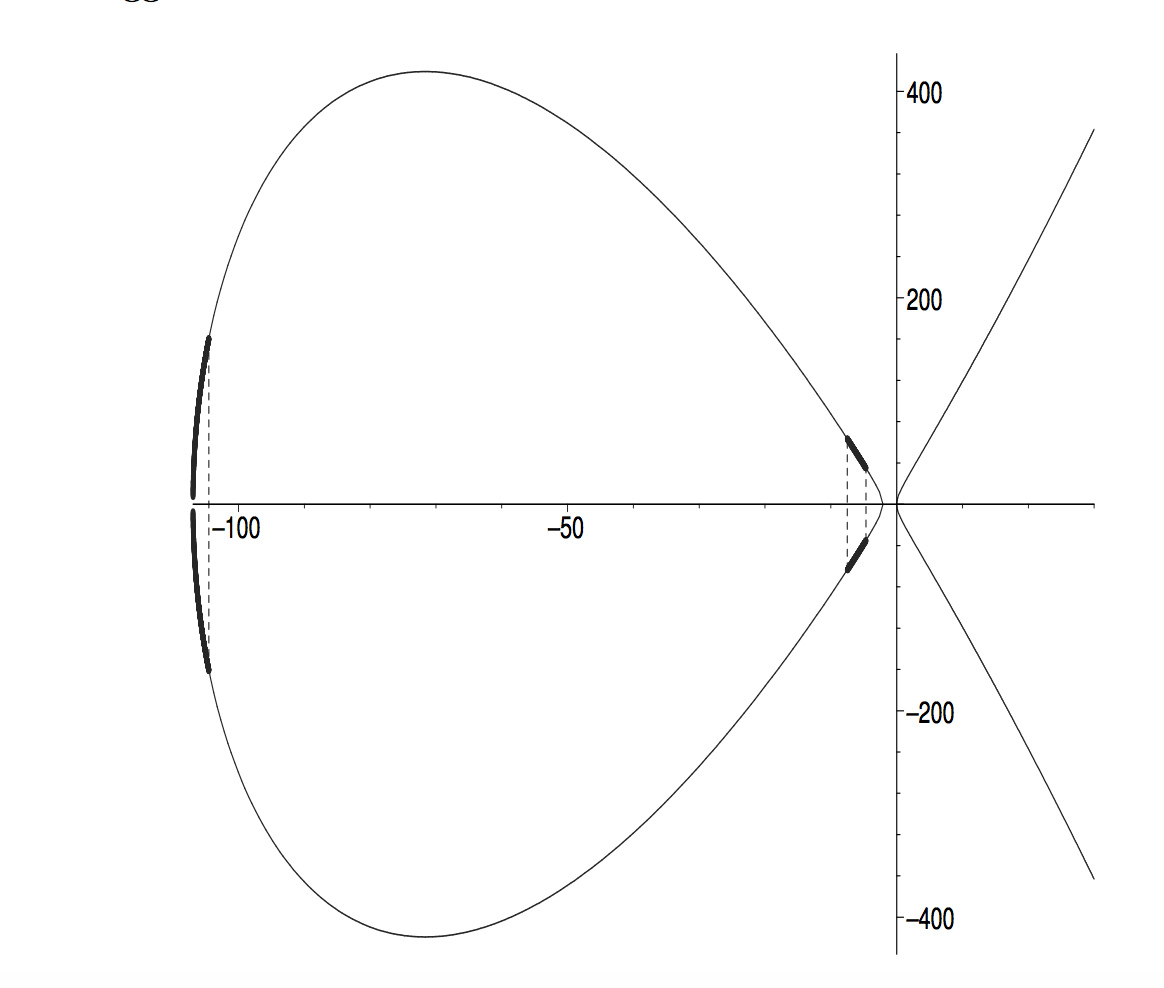
Точки
Бремнер и Маклауд изучили, что происходит, если мы заменяем
Поразительный пример того, как диофантовы уравнения с небольшими коэффициентами могут иметь огромные решения. Это внушает не просто трепет, а ощущение бездонности. Отрицательное решение десятой проблемы Гильберта означает, что рост решений при увеличении коэффициентов — это невычислимая функция, потому что если бы она была вычисляемой, то у нас был бы простой алгоритм решения диофантовых уравнений, а его не существует (ни простого, ни сложного). Соответствие
Вот такое удивительно хитрое небольшое уравнение.
Благодарю пользователя MrShoor, приславшего мне ссылку на эту интересную статью.