Доброго времени суток, дорогой читатель!
В данной статье мы разработаем нейронную сеть, которая сможет на неплохом уровне проходить созданную специально для неё игру.
Примечание: данная статья не объясняет термин "нейронная сеть" и всё, что с ним связано, а также не предоставляет базовую информацию об обучении сети методом трассировки. Рекомендуем кратко ознакомиться с этими понятиями до прочтения статьи
Цель — словить как можно больше кругов с зелёным ободком, избегая кругов с красным.
Условия:
После соприкосновения шар пропадает, а игроку начисляются соответствующие очки.
Для того, чтобы ИИ смог принять решение, куда двигаться игроку, нужно для начала получить данные об окружающей среде. Для этого создадим специа��ьные сканеры, представляющие из себя прямые линии. Первый сканер расположен под углом 180 градусов по отношению к нижней границе поля.
Их будет 68: первые 32 — реагируют на бомбы (красные окружности), следующие 32 — реагируют на яблоки (зелёные окружности), и последние 4 — принимают данные о нахождении границ поля относительно игрока. Назовём эти 68 сканера входными нейронами будущей нейронной сети (рецепторный слой).
Длина первых 64 сканеров 1000px, остальные 4 соответствуют делению поля пополам по соответствующей грани симметрии
 Сектор (1/4) области видимости ИИ
Сектор (1/4) области видимости ИИ

На рисунке: входные нейроны, получающие значения со сканеров
Значения на сканерах нормируется, т.е. приводится к диапазону [0, 1], причем чем ближе пересекающий сканер объект находится к игроку, тем большее значение передаётся сканеру.
Итак, для обучения НС было принято использовать алгоритм трассировки (опорных путей).
Примечание: в целях упрощения процесса обучения опущено построение матриц следование
Приступим:
Выполнив приведённый выше алгоритм, получим нейронную сеть, представленную на рисунке ниже
* Но это ещё не всё. Важно правильно интерпретировать результат, а именно (Y — массив выходных нейронов):
Таким образом, мы создали и автоматически обучили нейронную сеть, которая лежит в основе ИИ игрока на gif'ке вверху статьи
Весть код доступен (реализация игры и ИИ) по ссылке: Ссылка на гитхаб Ivan753/Learning
На этом всё. Спасибо за внимание!
В данной статье мы разработаем нейронную сеть, которая сможет на неплохом уровне проходить созданную специально для неё игру.

Примечание: данная статья не объясняет термин "нейронная сеть" и всё, что с ним связано, а также не предоставляет базовую информацию об обучении сети методом трассировки. Рекомендуем кратко ознакомиться с этими понятиями до прочтения статьи
Начало: описание правил игры
Цель — словить как можно больше кругов с зелёным ободком, избегая кругов с красным.
Условия:
- Красных окружностей вылетает на поле в два раза больше, чем зелёных;
- Зелёные окружности остаются в пределах поля, красные — вылетают за пределы и ликвидируются;
- Зелёный и красные окружности могут сталкиваться и отталкиваться с себе подобными;
- Игрок — жёлтый шар на экране, может передвигаться в пределах поля.
После соприкосновения шар пропадает, а игроку начисляются соответствующие очки.
Далее: проектируем ИИ
Рецепторы
Для того, чтобы ИИ смог принять решение, куда двигаться игроку, нужно для начала получить данные об окружающей среде. Для этого создадим специа��ьные сканеры, представляющие из себя прямые линии. Первый сканер расположен под углом 180 градусов по отношению к нижней границе поля.
Их будет 68: первые 32 — реагируют на бомбы (красные окружности), следующие 32 — реагируют на яблоки (зелёные окружности), и последние 4 — принимают данные о нахождении границ поля относительно игрока. Назовём эти 68 сканера входными нейронами будущей нейронной сети (рецепторный слой).
Длина первых 64 сканеров 1000px, остальные 4 соответствуют делению поля пополам по соответствующей грани симметрии
 Сектор (1/4) области видимости ИИ
Сектор (1/4) области видимости ИИ
На рисунке: входные нейроны, получающие значения со сканеров
Значения на сканерах нормируется, т.е. приводится к диапазону [0, 1], причем чем ближе пересекающий сканер объект находится к игроку, тем большее значение передаётся сканеру.
Алгоритм для получения данных сканерами и его реализация на JS
Итак, сканер — прямая. У нас есть координаты одной из её точек (координаты игрока) и угол относительно оси OX, вторую точку мы можем получить, используя тригонометрические функции sin и cos.
Отсюда получаем направляющий вектор прямой, а значит можем построить канонический вид уравнения этой прямой.
Чтобы получить значение на сканер, нужно посмотреть, пересекает ли какой-нибудь шар эту прямую, а значит, нужно представить уравнение прямой в параметрическом виде и подставить всё это в уравнения окружности, последовательно для каждой окружности для поля.
Если привести эту подстановку к общему виду, получится параметрической уравнение относительно a, b и с, где эти переменные — коэффициенты квадратного уравнения, начиная с квадрата соответственно.
Предлагаем читателю более подробно ознакомиться с этим алгоритмом самостоятельно, используя простейшие определения линейной алгебры
Ниже представлен код сканеров
Отсюда получаем направляющий вектор прямой, а значит можем построить канонический вид уравнения этой прямой.
Чтобы получить значение на сканер, нужно посмотреть, пересекает ли какой-нибудь шар эту прямую, а значит, нужно представить уравнение прямой в параметрическом виде и подставить всё это в уравнения окружности, последовательно для каждой окружности для поля.
Если привести эту подстановку к общему виду, получится параметрической уравнение относительно a, b и с, где эти переменные — коэффициенты квадратного уравнения, начиная с квадрата соответственно.
Предлагаем читателю более подробно ознакомиться с этим алгоритмом самостоятельно, используя простейшие определения линейной алгебры
Ниже представлен код сканеров
Ball.scaners: { //сканеры
length: 1000,
i: [], //значения на сканерах
get_data: function(){ //Ball.scaners.get_data / Получение данных со сканеров
var angl = 0;
var x0 = Ball.x,
var y0 = Ball.y;
var l = Ball.scaners.length;
for(let k = 0; k < 32; k++){
x1 = l*Math.cos(angl),
y1 = l*Math.sin(angl);
Ball.scaners.i[k] = 0;
for(i = 0; i < bombs.length; i++){
if(((k >= 0) && (k <= 8) && (bombs[i].x < x0) && (bombs[i].y < y0)) || ((k >= 8) && (k <= 16) && (bombs[i].x > x0) && (bombs[i].y < y0)) || ((k >= 16) && (k <= 24) && (bombs[i].x > x0) && (bombs[i].y > y0)) || ((k >= 24) && (k <= 32) && (bombs[i].x < x0) && (bombs[i].y > y0))){ //Проверка областей видимости сканеров
var x2 = bombs[i].x,
y2 = bombs[i].y;
var p = true; //проверка на наличие решения
var pt = true; //проверка на наличие ДВУХ корней
var t1, t2;
var a = x1*x1 + y1*y1,
b = 2*(x1*(x0 - x2) + y1*(y0 - y2)),
c = (x0 - x2)*(x0 - x2) + (y0 - y2)*(y0 - y2) - bombs[i].r*bombs[i].r;
//------------------------------Проверка восьми возможных случаев
if((a == 0) && (b != 0)){
t = -c/b;
pt = false;
}
if((a == 0) && (b == 0)){
p = false;
}
if((a != 0) && (b != 0) && (c == 0)){
t1 = 0;
t2 = b/a;
}
if((a != 0) && (b == 0) && (c == 0)){
t1 = 0;
pt = false;
}
if((a != 0) && (b == 0) && (c != 0)){
t1 = Math.sqrt(c/a);
t2 = -Math.sqrt(c/a);
}
if((a != 0) && (b != 0) && (c != 0)){
var d = b*b - 4*a*c;
if(d > 0){
t1 = (-b + Math.sqrt(d))/(2*a);
t2 = (-b - Math.sqrt(d))/(2*a);
}
if(d == 0){
t1 = -b/(2*a);
}
if(d < 0){
p = false;
}
}
//-----------------------------------
if(p == true){
if(pt == true){
let x = t1*x1 + x0;
let y = t1*y1 + y0;
let l1 = Math.pow((x - Ball.x), 2)+Math.pow((y - Ball.y), 2);
x = t2*x1 + x0;
y = t2*y1 + y0;
let l2 = Math.pow((x - Ball.x), 2)+Math.pow((y - Ball.y), 2);
if(l1 <= l2){
Ball.scaners.i[k] += 1 - l1/(l*l);
}else{
Ball.scaners.i[k] += 1 - l2/(l*l);
}
}else{
let x = t1*x1 + x0;
let y = t1*y1 + y0;
Ball.scaners.i[k] += 1 - (Math.pow((x - Ball.x), 2)+Math.pow((y - Ball.y), 2))/(l*l);
}
}else{
Ball.scaners.i[k] += 0;
}
}else{
continue;
}
}
angl += Math.PI/16;
}
//!---------------Для зелёных
for(k = 32; k < 64; k++){
x1 = l*Math.cos(angl),
y1 = l*Math.sin(angl);
Ball.scaners.i[k] = 0;
for(i = 0; i < apples.length; i++){
if(((k >= 32) && (k <= 40) && (apples[i].x < x0) && (apples[i].y < y0)) || ((k >= 40) && (k <= 48) && (apples[i].x > x0) && (apples[i].y < y0)) || ((k >= 48) && (k <= 56) && (apples[i].x > x0) && (apples[i].y > y0)) || ((k >= 56) && (k <= 64) && (apples[i].x < x0) && (apples[i].y > y0))){
var x2 = apples[i].x,
var y2 = apples[i].y;
var p = true; //проверка на наличие решения
var pt = true; //проверка на наличие ДВУХ корней
var t1, t2;
var a = x1*x1 + y1*y1,
b = 2*(x1*(x0 - x2) + y1*(y0 - y2)),
c = (x0 - x2)*(x0 - x2) + (y0 - y2)*(y0 - y2) - apples[i].r*apples[i].r;
//------------------------------Проверка восьми возможных случаев
if((a == 0) && (b != 0)){
t = -c/b;
pt = false;
}
if((a == 0) && (b == 0)){
p = false;
}
if((a != 0) && (b != 0) && (c == 0)){
t1 = 0;
t2 = b/a;
}
if((a != 0) && (b == 0) && (c == 0)){
t1 = 0;
pt = false;
}
if((a != 0) && (b == 0) && (c != 0)){
t1 = Math.sqrt(c/a);
t2 = -Math.sqrt(c/a);
}
if((a != 0) && (b != 0) && (c != 0)){
var d = b*b - 4*a*c;
if(d > 0){
t1 = (-b + Math.sqrt(d))/(2*a);
t2 = (-b - Math.sqrt(d))/(2*a);
}
if(d == 0){
t1 = -b/(2*a);
}
if(d < 0){
p = false;
}
}
//-----------------------------------
if(p == true){
if(pt == true){
let x = t1*x1 + x0;
let y = t1*y1 + y0;
let l1 = Math.pow((x - Ball.x), 2)+Math.pow((y - Ball.y), 2);
x = t2*x1 + x0;
y = t2*y1 + y0;
let l2 = Math.pow((x - Ball.x), 2)+Math.pow((y - Ball.y), 2);
if(l1 <= l2){
Ball.scaners.i[k] += 1 - l1/(l*l);
}else{
Ball.scaners.i[k] += 1 - l2/(l*l);
}
}else{
let x = t1*x1 + x0;
let y = t1*y1 + y0;
Ball.scaners.i[k] += 1 - (Math.pow((x - Ball.x), 2)+Math.pow((y - Ball.y), 2))/(l*l);
}
}else{
Ball.scaners.i[k] += 0;
}
}else{
continue;
}
}
angl += Math.PI/16;
}
Ball.scaners.i[64] = (1000 - Ball.x) / 1000; //левая граница
Ball.scaners.i[65] = Ball.x / 1000; //правая граница
Ball.scaners.i[66] = (500 - Ball.y) / 500; //верхняя граница
Ball.scaners.i[67] = Ball.y / 500; //нижняя граница
}
}
Проектирование нейронной сети
Итак, для обучения НС было принято использовать алгоритм трассировки (опорных путей).
Примечание: в целях упрощения процесса обучения опущено построение матриц следование
Приступим:
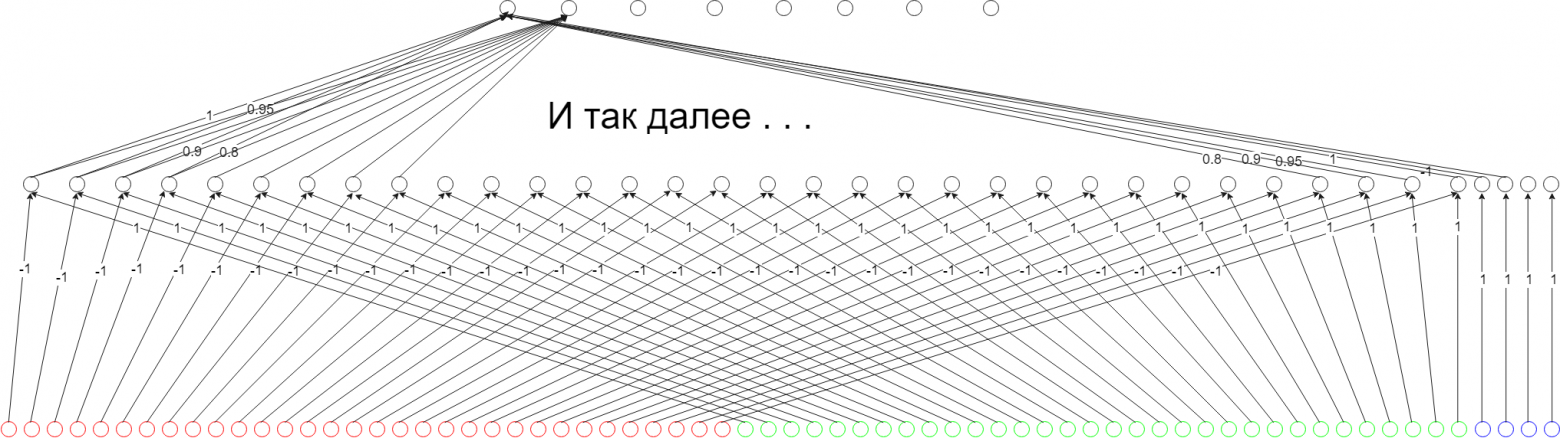
- На выходе сети представим 8 нейронов, отвечающих за направления: первый — лево, второй — лево+верх, третий — верх, четвёртый — верх+право, пятый — право и тд;
- Пусть положительное значение на нейроне значит, что следует двигаться в сторону, которая за ним закреплена, а отрицательное — обратное;
- Нам важно как-то объединить значения со сканеров, находящихся под одним углом относительно нижнего края поля. Так как при отрицательно выходе ИИ будет отталкиваться от этого направления, введём дополнительный слой (скрытый, между входным и выходным), ��оторый будет складывать значения нейронов, отражающих попарно соответствующие сканеры, причём значения с красных нейронов будем брать со знаком "-";
- Очевидно, что на движение влево главный образом влияет информация, которая находится слева от игрока (не только, но это будет учтено позже (*)) — значит связываем 8 нейронов скрытого слоя, находящихся слева, с нейроном, отвечающим за движение влево. Связи устанавливаем так: нейрон, отвечающих сканеру, расположенному параллельно границе поля, назначается вес 1, далее соседним двум нейронам назначается вес 0.95, соседним через одного вес 0.9, и, наконец, крайним в данном секторе вес 0.8;
- Нейроны границ тоже учитываем: проводим к выходам связи от тех граничных нейронов, границы которых могу влиять на движение.
- То же самое проделывает с оставшимися семью нейронами выходного слоя.
Выполнив приведённый выше алгоритм, получим нейронную сеть, представленную на рисунке ниже

* Но это ещё не всё. Важно правильно интерпретировать результат, а именно (Y — массив выходных нейронов):
Ball.v.x = -(Y[0] - Y[4]) + (-(Y[1] - Y[5]) + (Y[3] - Y[6]))*0.5;
Ball.v.y = -(Y[2] - Y[6]) + (-(Y[3] - Y[7]) + (Y[5] - Y[1]))*0.5;
Таким образом, мы создали и автоматически обучили нейронную сеть, которая лежит в основе ИИ игрока на gif'ке вверху статьи
Весть код доступен (реализация игры и ИИ) по ссылке: Ссылка на гитхаб Ivan753/Learning
На этом всё. Спасибо за внимание!