How to become an author
Search
Write a publication
Pull to refresh

AES — американский стандарт шифрования. Часть I

Reading time9 min
Views13K
Algorithms*Information Security*Cryptography*Mathematics*
image

Прочие статьи цикла
AES — американский стандарт шифрования. Часть I
АES — американский стандарт шифрования. Часть II
AES — американский стандарт шифрования. Часть III
AES — американский стандарт шифрования. Часть IV
AES — американский стандарт шифрования. Часть V. Атака


Эта публикация вызвана необходимостью дать возможность обучаемым изучать и моделировать процессы шифрования/расшифрования и дешифрования последнего стандарта США. Ознакомление с имеющимися публикациями в сети не соответствуют программе обучения в силу их поверхностного подхода, неполноты изложения, и отсутствия должной строгости. Например, нигде не встречается выбор и задание примитивного элемента, формирующего поле, без чего работу и подготовку специалиста, особенно криптоаналитические явления и процессы, организовать и моделировать невозможно. В этой работе используется описание, несколько отличное от оригинала AES, представленного FIPS PUB 197. Здесь описывается шифр AES, с использованием матриц над GF(28), но примечания работы сохраняются, т. е. шифр реализуется над конечным расширенным полем GF (28). На русском языке достаточно полная и доступная версия шифра изложена Зензиным О.С. и Ивановым М.А.

Математические основы стандарта шифрования AES США


AES – блочный шифр с длиной блоков равной 128 битам, и шифр поддерживает ключи длиной $N_к$, равной 128, 192 или 256 бит. AES – это шифр с итерационным ключом: состоит из повторного применения раундового преобразования состояния блока State шифруемого текста. Число раундов шифра обозначается $N_r$ зависит от длины ключа ($N_r = 10$ для ключа 128 битов, $N_r= 12$ для ключа 192 бита и $N_r = 14$ для ключа 256 бит).

Шифр AES преобразует исходное состояние блока, обозначаемое символом S (State) и принадлежащее множеству матриц {M4(GF(28))} (то есть S є{M4(GF (28))} – матрица 4 × 4 байта, с ее элементами (коэффициентами) в GF (28)), к другому шифрованному состоянию в {M4 (GF (28))}.

Пример 1. Блок данных длиной в 128 = 4·32, 4 слова по 32 разряда представляется квадратной таблицей байтов из 4-х строк и 4-х столбцов. Каждая строка содержит байты из 4-х разных 32 разрядных слов, а столбец – байты одного и того же 32-разрядного слова. Весь квадрат образован 4×4 = 16 байтами, которые могут обрабатываться как самостоятельные единицы.

Именно такой подход к представлению данных определяет и обеспечивает байт-ориентированную структуру шифра и обработку данных. Ключ шифра K расширяется в $N_r+1$ подключей, обозначаемых матрицей Ki ={M4(GF(28))}, принадлежащей множеству {M4 (GF(28))}, (i = 0, 1, ..., Nr). Перестановка элементов в матрице S, возникающая при операции сдвига строк обозначена символом р(х).

Представление данных, выбранное для элементов поля GF(28)


В шифре AES используется байтовая структура данных. Представление, выбранное в [1] из векторного пространства GF(28), соответствующего полю GF(28)[X]/< φ(x) >, где φ(x) – неприводимый многочлен,

$φ(x) = x^8 + x^4 + x^3 + x + 1$

. Для удобства и лучшего понимания изучаемого материала, а для уяснения деталей выполнения вычислений с карандашом в руках ниже приводятся многочисленные числовые примеры и следующая таблица 1.

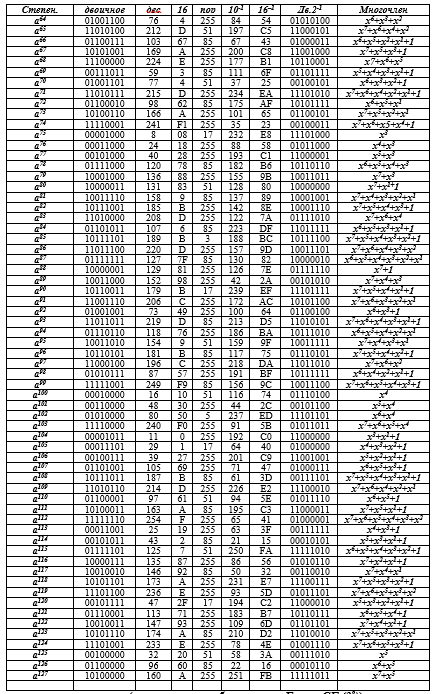
Таблица 1. Соответствие десятичных, шестнадцатеричных, двоичных чисел и многочленов

В работе используются четыре представления для обозначения каждого элемента расширенного поля в GF(28), которые являются эквивалентными одно другому.

Представление данных, используемых в шифре AES


Выберем десятичное целое число, эквивалент которого будем представлять
различными формами в других системах счисления:

1. 21210, десятичным видом – числом в 10-ой системе счисления.

2. {11010100}b, представление элементов сообщения двоичным вектором – элементом векторного пространства GF(28) двоичных векторов,

3. $x^7+ x^6 + x^4 + x^2$, многочленное представление – элементом поля Галуа GF [28], соответствующим двоичному вектору,

4. {D4}16, – шестнадцатеричное представление – числом в 16-системе счисления,

⊕ – операция поразрядного суммирования векторов из GF(28) по mod2 (без переноса 1 в старший разряд).
⊗ – операция умножения элементов (векторов, многочленов, чисел) из поля GF(28)

Алгоритм стандарта AES и шифра RIJNDAEL оперирует с байтами информации, которые отождествляются с элементами конечного поля Галуа GF(28). Степень расширения простого поля GF(2) равна 8. Все элементы расширенного поля при представлении их многочленами имеют показатель степень не более семи (≤ 7).

Достигается такое положение приведением всех результатов действий с элементами поля по модулю неприводимого многочлена степени 8, который является формирующим многочленом для этого поля. Кроме неприводимого многочлена для построения поля необходимо задавать примитивный элемент.

В рассматриваемом алгоритме примитивный элемент задан (его порядок должен быть равен порядку мультипликативной группы поля), а многочлен фиксирован и имеет вид φ(x). Не располагая этими характеристикам, работать со стандартом не получится

$φ(x) = x^8 + x^4 + x^3 + x + 1$

или 1{1b} в 16-ричной форме.
Шестнадцатеричная запись неприводимого многочлена 1{1b} использует 9 разрядов и многочлен φ(x) не принадлежит полю GF(28).
Таблица П1 представления элементов поля GF(28) (в конце текста в Приложении).
В таблице П1 размещены все элементы поля в порядке возрастания показателя степени примитивного элемента (α = 000000112 = 310), мультипликативный порядок которого равен 255.

Рассмотрим примеры выполнения арифметических операций над элементами поля при различных представлениях этих элементов. Любой байт исходного текста (элемент поля) формально можно представить строкой символов $a_i, i = 0(1)7$, коэффициентов двоичного вектора в виде:

${a_7, a_6, a_5, a_4, a_3, a_2, a_1, a_0}, a_i∊GF(2), i = 0(1)7.$


Пример 2. Элемент расширенного поля GF(28) задан в виде двоичного вектора:

${a_7, a_6, a_5, a_4, a_3, a_2, a_1, a_0}, a_i∊GF(2), i = 0(1)7$


Описание многочленом этого элемента имеет вид:

$(x) = a_7 x^7 + a_6 x^6 + a_5 x^5 + a_4x^4 + a_3 x^3 + a_2 x^2 + a_1 x^1 + a_0 x^0$


Если доопределить значения ai двоичными значениями, i = 0(1)7, например, так ${a_7, a_6, a_5, a_4, a_3, a_2, a_1, a_0}$ = {11000001}2, то получим многочлен

$α(x) = x^7 + x^6 +1,$

так как $ a_5 = a_4 =a_3 =a_2 =a_1 = 0.$

Шестнадцатеричное представление этого элемента α16 = {с1}={11000001}, а десятичное

α10 = $2^7 + 2^6 + 2^0$ = 128 + 64 + 1 = 19310.

При выбранном примитивном элементе поля степенное представление
αi ={с1}= α178.
Входим в таблицу П1 элементов поля GF(28) со значением α178 и в соответствующих столбцах для этой строки находим описанные представления, а также другие характеристики этого элемента поля. Для понимания возможных преобразований с элементами поля рассмотрим операции с его элементами в деталях.

Суммирование элементов поля GF(28)


Сложение в рассматриваемом поле представляет операцию поразрядного суммирования значений разрядов слагаемых без переноса единицы в старший разряд. Это операция исключающего ИЛИ (EXOR – EXLUSIV OR) часто обозначается просто XOR. В модулярной арифметике такое сложение называется суммированием по модулю два (mod2).

Пример 3. Выберем в качестве операндов многочлены
$A(x) = x^7+ x^6 + 1;$
$B(x) = x^3 + x^2 + x^0.$
Двоичное представление суммы многочленов по модулю два имеет вид
[A(x)⊕B(x)]mod2 = {11000001}⊕ {00001101} = {11001100};

16-ричное представление {c1}⊕{0D}={cc}sub>16=α55;
степенное представление α178 + α238 = α55· {α123 + α183} = α55· 1 = α55.

Представление многочленами
$(x^7+x^6+1)⊕ (x^3+x^2+1)(mod2)= (x^7+x^6+x^3+x^2+2)(mod2)=x^7+x^6+x^3+x^2.$
Заметим, что при сложении операндов степень многочлена результата не
увеличивается, и необходимость приведения его по модулю неприводимого многочлена поля φ(x) не возникает. Коэффициенты результата приводятся по модулю два, т. е. все четные коэффициенты обращаются в нуль.

В полях характеристики 2 действия сложения и вычитания операндов равнозначны. Для каждого элемента поля в аддитивной группе обратным к нему (противоположным) является он сам. Так, для элемента (а) противоположным является (-а), так как а + (-а) = 0. Нулевой элемент (единица аддитивной группы поля, нейтральный элемент) в шестнадцатеричном виде – это {00}16.

Умножение элементов поля GF(28)


Операция обычного умножения операндов (в отличие от модулярного ⊗) обозначается точкой между операндами, или знак умножения вообще опускается, когда не возникает опасности разночтения. Операнды в двоичном представлении умножаются по обычным правилам «столбиком». Будем перемножать те же, что и ранее операнды.

Пример 4. Умножение операндов в двоичном представлении
А(х)· В(х) = {c1}·{0d}

Остаток от деления получает вид двоичного, многочленного и 16-ричного представлений (как элемент поля)
R(x) = 01011 10102 = $x^7+ x^5+ x^4+ x^3+ x $= {ba}16. Старший разряд остатка равен нулю и не учитывается.
Степенное представление здесь не приводим, но по таблице П1 его можно найти.

Остаток от деления на неприводимый многочлен φ(x) в его двоичном представлении результата умножения операндов принимаем в качестве произведения операндов как элементов поля GF(28).

Выполним умножение операндов в представлении многочленами.

Пример 5. Умножение операндов элементов поля в многочленном представлении
А(х) ⊗ В(х) = {c1}⊗{0d}
A(x) ⊗ B(x) = $(x^7+ x^6+ 1)⊗(x^3+ x^2+1) $(moddφ(x),2) =
=(x10+$ x^9+ x^9+ x^8+ x^7+ x^6+ x^3+ x^2+1)$(moddφ(x),2) =
=(x10+$ x^8+ x^7+ x^6+ x^3+ x^2+1)$(moddφ(x),2).

Здесь символ (moddφ (x),2) обозначает приведение по двойному модулю: многочлен по модулю φ(x), а его коэффициенты по модулю два, т.е. четные коэффициенты обнуляются. Получившаяся степень (deg(A(x)⊗ B(x)) =10) результата произведения выводит (этот многочлен — результат) за пределы поля. Чтобы результат принадлежал полю, его приводят (редуцируют, делят) по модулю неприводимого многочлена. Выполним такое деление обычным способом (уголком)

Пример 6. Необходимость деления многочленов возникает при
их умножении А(х)⊗В(х)/ φ(x).(Операции деления в поле нет, когда надо что-то поделить, это что-то умножают на обратный элемент делителя в поле)

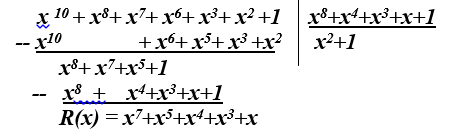
– остаток отделения на φ(x) принадлежит полю GF(28), и его принимаем в качестве окончательного результата $R(x) = x^7+x^5+x^4+x^3+x$ модулярного умножения.

Иначе умножение A(x)⊗B(x) представимо как
$(x^2 + 1)(x^8 + x^4+ x^3+ x +1)⊕ (x^7+ x^5+ x^4+ x^3+ x) = = (x^2+1)·φ(x)⊕R(x)$ = {ba}16=α161,
где R(x) остаток и degR(x)< deg φ(x).
Степенное представление для получения произведения элементов поля самое удобное.
A(x)· B(x) = α178· α238 = α(178+238) = α416 = α161α255 =α161 = {ba}16.

Для любого ненулевого элемента β поля справедливо β·1 =β. Мультипликативной единицей в GF(28) является элемент {01}16 =α255.
Все вычисленные произведения для различных представлений операндов эквивалентны (преобразуются в один элемент поля со значением {ba}16).

Наряду с обычным (классическим) рассмотрением операции умножения элементов в двоичном поле существует более удобная схема. Именно такая схема и реализована в стандарте AES.

Рассмотрим сущность этого способа умножения


Пример 7. Другой способ умножения в конечном поле. Пусть задан произвольный многочлен седьмой степени
$A(x) = a_7x^7+ a_6x^6+ a_5x^5+ a_4x^4+ a_3x^3+ a_2x^2+ a_1x+ a_0$
и значения его коэффициентов $(a_7 a_6 a_5 a_4 a_3 a_2 a_1 a_0) = (10000011)_2$.

Умножим его на $x$ и получим $a_7x^8+ a_1x^2+ a_0x$. Этот результат не принадлежит полю GF(28) степень его многочлена больше 7 и его необходимо привести по модулю φ(x) = 1{1b}, после чего такое произведение станет элементом поля GF(28).

С этой целью определяют значение $ a_7 $, если $а_7 = 0$ то результат уже принадлежит полю, если же $ a_7 = 1$, то достаточно вместо деления выполнить лишь вычитание A(x)x – φ(x) или операцию XOR для произведения A(x)x с φ(x).

В этом случае при записи A(x) в сдвиговом регистре умножению на x полинома A(x), т.е. $A(x)⊗{00000010} = A(x)⊗{02}$ соответствует сдвиг полинома A(x) на один разряд в сторону старших разрядов (влево, т.е. увеличение вдвое) и, если требуется, применяется операция XOR с неприводимым многочленом поля 1{1b}16 =φ(x).

В алгоритме стандарта шифрования введена операция (функция) xtime( ), которая по существу и выполняет умножение полинома на х, так как это описано ранее. Многократное применение xtime обеспечивает умножение на x8. Далее вычисляя сумму различных степеней, можно получить результат умножения произвольных элементов поля GF(28).

Пример 8. Перемножим многочлены A(x) = {c1}16 и B(x) = {11}16, используя их 16-ичные представления и представляя суммой {11} ={10⊕01}.
{c1}⊗{11}={11000001}⊗{00010001}={c1}⊗{10⊕01}={a4}⊕{c1}=01100101 ={65}16.

Детализируем все действия. Элемент х в поле GF(28) имеет представление
x = {02}16=(00000010)2.
{c1}⊗{11}={c1}⊗{10}⊕{c1}⊗{01}= α178· α100⊕α178· α0={a4}⊕{c1}, так как α178· α100=α(178+100-255)=α23={a4}

Тогда умножение на него приводит просто к сдвигу первого операнда на 1 разряд влево.
{c1}⊗ {02} = xtime{c1} = 11000001⊗ 00000010= 110000010 — 9-ти разрядное двоичное число. Этот результат выходит за пределы нашего поля. Его возвращают вычитанием неприводимого многочлена поля φ(х), преобразуя в элемент поля. Итоговый результат 10011001 = {99}

$\begin{array}{r} - \begin{array}{r} 110000010\\ 100011011\\ \end{array} \\ \hline \begin{array}{r} 10011001 \end{array} \end{array}$


{c1}⊗ {04} = xtime(99) = 10011001⊗ 00000010 =100110010 — 9-ти разрядное двоичное число. Этот результат выходит за пределы нашего поля. Его возвращают вычитанием неприводимого многочлена поля φ(х), преобразуя в элемент поля. Итоговый результат 00101001 = {29}

$\begin{array}{r} - \begin{array}{r} 100110010\\ 100011011\\ \end{array} \\ \hline \begin{array}{r} 00101001 \end{array} \end{array}$


Очередной шаг процедуры
{c1}⊗ {08} = xtime(29) = 00101001⊗ 00000010 = 0101 0010 = {52}.
Здесь результат не суммируем с φ(x), так как коэффициент $a_7 = 0$.

И еще один шаг
{c1}⊗ {10} = xtime(52) = 01010010⊗00000010 = 10100100 = {a4}16.
Здесь также не суммируем с φ(x), так как коэффициент $a_7 = 0$.
Таким образом, найдено значение первого слагаемого в сумме для исходного
выражения, где второе слагаемое равно {c1}16.
Теперь находим окончательно
{c1}⊗ {11} = {c1}⊗ {10}⊕ {c1}⊗ {01} = {a4} ⊕ {c1} =10100100⊕ 11000001 = {65} или

$\begin{array}{r} - \begin{array}{r} 10100100\\ 11000001\\ \end{array} \\ \hline \begin{array}{r} 01100101 \end{array} \end{array}$



проверка обычным умножением (степенное представление)
A(x)∙ B(x) = {c1}∙{11} = α178∙α4 = α182
(по таблицам находим в строке для α1182) α182 соответствует {65}16.

Еще большего эффекта при производстве вычислений можно достигнуть, если укрупнить элементы, с которыми выполняются манипуляции. Так в криптоалгоритме RIJNDAEL используются 32-разрядные (4-х-байтовые) слова. Составляющие байт разряды не анализируются по отдельности. Такой подход позволяет 4-байтовому слову в соответствие поставить многочлен А(х) степени не более трех, и коэффициенты которого лежат в поле GF(28).

Операция умножения таких слов
$A(x) = a_3x^3 + a_2x^2 + a_1x + a_0$ и
$B(x) = b_3x^3 + b_2x^2 + b_1x+b_0$,
где $a_i, b_i$єGF(28), i = 0(1)3, выполняется по модулю многочлена степени не более четырех. Взятие результата произведения по модулю неприводимого многочлена степени 4 обеспечивает всегда получение результата произведения, как элемента поля.

В качестве такого многочлена выбран многочлен $ψ(x) = x^4 + 1$. Он имеет наиболее простую запись, и для него справедливо
$x_i (mod(x^4+1)) = x_i (mod4)$.
Последнее свойство оказывается очень полезным при вычислениях.
Для рассматриваемых многочленов операция сложения выполняется аналогично (XOR поразрядное по mod2)
$A(x)⊕ B(x) = (a_3⊕ b_3) x^3 ⊕ (a_2⊕ b_2) x^2 ⊕ (a_1⊕ b_1)x ⊕ (a_0⊕ b_0)$.

Умножение многочленов.
$A(x)⊗ B(x) = C(x) = (c_6x^6 ⊕ c_5x^5 ⊕ c_4x^4⊕ c_3x^3 ⊕ c_2x^2 ⊕ c_1x^1 ⊕ c_0) mod(x^4+1)$.
Коэффициенты $c_j, j = 0(1)6$ определяются из соотношений
$C_0 = a_0⊕b_0$,
$C_1 = a_1b_0⊕ a_0b_1$,
$C_2 = a_2b_0 ⊕ a_1b_1⊕a_0b_2$,
$C_3 = a_3b_0⊕ a_2b_1⊕ a_1b_2⊕a_0b_3$,
$C_4 = a_3b_1⊕ a_2b_2⊕ a_1b_3$,
$C_5 = a_3b_2⊕ a_2b_3$,
$C_6 = a_3b_3$.

Окончательно результатом D(x) умножения ⊗ двух многочленов по модулю $x^4+1$ будет
$D(x) = A(x)⊗B(x) = d_3x^3 ⊕ d_2x^2 ⊕ d_1x ⊕ d_0$, где
$d_0 = a_0b_0⊕ a_3b_1⊕ a_2b_2⊕ a_1b_3$,
$d_1 = a_1b_0⊕ a_0b_1⊕ a_3b_2⊕ a_2b_3$,
$d_2 = a_2b_0⊕ a_1b_1⊕ a_0b_2⊕ a_3b_3$,
$d_3 = a_3b_0⊕ a_2b_1⊕ a_1b_2⊕ a_0b_3$,
или более кратко в векторно – матричной записи,

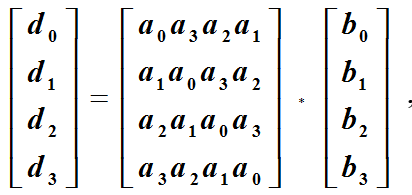
выполним умножение В(х) на х по $mod(х^4+1)$, учитывая свойства многочлена. Такому умножению, как и ранее, соответствует циклический сдвиг байтов в пределах слова в направлении старшего байта. Так как
$x^4mod(x^4 + 1) = x_i mod4 = x^0 = 1$, то
$x∙ B(x) = b_2x^3+ b_1x^2+ b_0x+ b_3 => x∙(b_3 b_2 b_1 b_0)$
реализуется циклический сдвиг байтов.

Приложение


Таблица П1 — расширенного поля, неприводимый многочлен φ(х)=Р (х), примитивный элемент α=316



Tags:
Hubs:
Total votes 15: ↑8 and ↓7+4
Comments7
20
Karma
-0.5
Rating
Ваулин Арис Ефимович @VAE

Пользователь

Send message

Articles

Your account

Sections

Information

Services

Support
© 2006–2024, Habr