
Сортировку кучей (она же — пирамидальная сортировка) на Хабре уже поминали добрым словом не раз и не два, но это всегда была достаточно общеизвестная информация. Обычную бинарную кучу знают все, но ведь в теории алгоритмов также есть:
n-нарная куча; куча куч, основанная на числах Леонардо; дерамида (гибрид кучи и двоичного дерева поиска); турнирная мини-куча; зеркальная (обратная) куча; слабая куча; юнгова куча; биномиальная куча; и бог весть ещё какие кучи…
И умнейшие представители computer science в разные годы предложили свои алгоритмы сортировки с помощью этих пирамидальных структур. Кому интересно, что у них получилось — для тех начинаем небольшую серию статей, посвящённую вопросам сортировки с помощью этих структур. Мир куч многообразен — надеюсь, вам будет интересно.
Есть такой класс алгоритмов — сортировки выбором. Общая идея — неупорядоченная часть массива уменьшается за счёт того, что в ней ищутся максимальные элементы, которые из неё переставляются в увеличивающуюся отсортированную область.
Статья написана при поддержке компании EDISON.
Мы занимаемся разработкой мобильных приложений и предоставляем услуги по тестированию программного обеспечения.
Мы очень любим теорию алгоритмов! ;-)

Сортировка обычным выбором — это брутфорс. Если в поисках максимумов просто линейно проходить по массиву, то временнáя сложность такого алгоритма не может превысить O(n2).
Куча
Наиболее эффективный способ работать с максимумами в массиве — это организовать данные в специальную древовидную структуру, известную как куча. Это дерево, в котором все родительские узлы не меньше чем узлы-потомки.
Другие названия кучи — пирамида, сортирующее дерево.
Давайте разберём, как это можно легко и почти бесплатно представить массив в виде дерева.
Возьмём самый первый элемент массива и будем считатть, что это корень дерева — узел 1-го уровня. Следующие 2 элемента — это узлы 2-го уровня, правый и левый потомки корневого элемента. Следующие 4 элемента — это узлы 3-го уровня, правые/левые потомки второго/третьего элемента массива. Следующие 8 элементов — узлы 4-го уровня, потомки элементов 3-го уровня. И т.д. На этом изображении узлы бинарного дерева наглядно расположены строго под соответствующими элементами в массиве:

Хотя, деревья на диаграммах чаще изображают в такой развёртке:
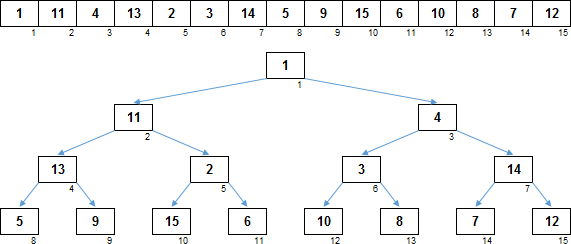
Если смотреть под таким углом, то тогда понятно почему сортировку кучей называют пирамидальной сортировкой. Хотя, это примерно тоже самое, как если шахматного слона называть офицером, ладью — турой, а ферзя — королевой.
Индексы потомков для i-го элемента определяются элементарно (если индекс самого первого элемента массива считать равным 0, как принято в подавляющем большинстве языков программирования):
Левый потомок: 2 × i + 1
Правый потомок: 2 × i + 2
(У меня на диаграммах и анимациях традиционно индексы массивов начинаются с 1, там формулы слегка отличаются: левый потомок:
Если получающиеся по этим формулам индексы потомков выходят за пределы массива, значит у i-го элемента потомков нет. Также может статься что у i-го элемента есть левый потомок (приходится на самый последний элемент массива, в котором нечётное количество элементов), но уже нет правого.
Итак, любой массив можно легко представить в виде дерева, однако это пока ещё не куча, потому что, в массиве некоторые элементы-потомки могут оказаться больше чем их элементы-родители.
Чтобы наше дерево, созданное на основе массива, стало кучей, его нужно как следует просеять.
Просейка
Душой сортировки кучей является просейка.
Просеивание для элемента состоит в том, что если он меньше по размеру чем потомки, объединённых в неразрывную цепочку, то этот элемент нужно переместить как можно ниже, а бо́льших потомков по ветке поднять наверх на 1 уровень.
На изображении показан путь просейки для элемента. Синим цветом обозначен элемент для которого осуществляется просейка. Зелёный цвет — бо́льшие потомки вниз по ветке. Они будут подняты на один уровень вверх, поскольку по величине превосходят синий узел, для которого делается просейка. Сам элемент из самого верхнего синего узла будет перемещён на место самого нижнего потомка из зелёной цепочки.
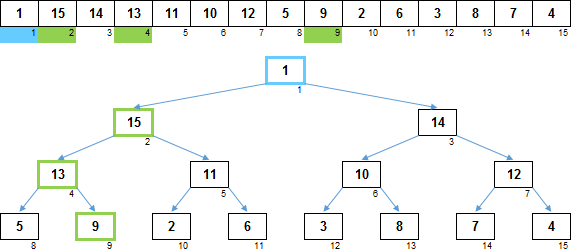
Просейка нужна для того, чтобы из обычного дерева сделать сортирующее дерево и в дальнейшем поддерживать дерево в таком (сортирующем) состоянии.
На этом изображении элементы массива перераспределены так, что он уже разложен именно в кучу. Хотя массив раскладывается в сортирующее дерево, сам он пока что не отсортирован (ни по возрастанию ни по убыванию), хотя все потомки в дереве меньше чем их родительские узлы. Но зато самый максимальный элемент в сортирующем дереве всегда находится в главном корне, что очень важно.
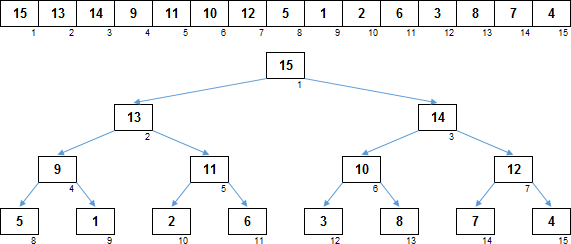
Сортировка кучей :: Heapsort
Алгоритм на самом деле простой:
- Этап 1. Формируем из всего массива сортирующее дерево. Для этого проходим справа-налево элементы (от последних к первым) и если у элемента есть потомки, то для него делаем просейку.
- Этап 2. Максимумы ставим в конец неотсортированной части массива. Так как данные в массиве после первого этапа представляют из себя сортирующее дерево, максимальный элемент находится на первом месте в массиве. Первый элемент (он же максимум) меняем с последним элементом неотсортированной части массива местами. После этого обмена максимум оказался своём окончательном месте, т.е. максимальный элемент отсортирован. Неотсортированная часть массива перестала быть сортирующим деревом, но это исправляется однократной просейкой — в результате чего на первом месте массива оказывается предыдущий по величине максимальный элемент. Действия этого этапа снова повторяются для оставшейся неупорядоченной области, до тех пор пока максимумы поочерёдно не будут перемещены на свои окончательные позиции.

Код на Питоне классической реализации пирамидальной сортировки:
# Основной алгоритм сортировки кучей
def HeapSort(data):
# Формируем первоначальное сортирующее дерево
# Для этого справа-налево перебираем элементы массива
# (у которых есть потомки) и делаем для каждого из них просейку
for start in range((len(data) - 2) / 2, -1, -1):
HeapSift(data, start, len(data) - 1)
# Первый элемент массива всегда соответствует корню сортирующего дерева
# и поэтому является максимумом для неотсортированной части массива.
for end in range(len(data) - 1, 0, -1):
# Меняем этот максимум местами с последним
# элементом неотсортированной части массива
data[end], data[0] = data[0], data[end]
# После обмена в корне сортирующего дерева немаксимальный элемент
# Восстанавливаем сортирующее дерево
# Просейка для неотсортированной части массива
HeapSift(data, 0, end - 1)
return data
# Просейка свеху вниз, в результате которой восстанавливается сортирующее дерево
def HeapSift(data, start, end):
# Начало подмассива - узел, с которого начинаем просейку вниз
root = start
# Цикл просейки продолжается до тех пор,
# Пока встречаются потомки, большие чем их родитель
while True:
child = root * 2 + 1 # Левый потомок
# Левый потомок за пределами подмассива - завершаем просейку
if child > end: break
# Если правый потомок тоже в пределах подмассива,
# то среди обоих потомков выбираем наибольший
if child + 1 <= end and data[child] < data[child + 1]:
child += 1
# Если больший потомок больше корня, то меняем местами
# при этом больший потомок сам становится корнем,
# от которого дальше опускаемся вниз по дереву
if data[root] < data[child]:
data[root], data[child] = data[child], data[root]
root = child
else:
breakСложность алгоритма
Чем хороша простая куча — её не нужно отдельно хранить, в отличие от других видов деревьев (например, двоичное дерево поиска на основе массива прежде чем использовать нужно сначала создать). Любой массив уже является деревом, в котором прямо на ходу можно сразу определять родителей и потомков. Сложность по дополнительной памяти O(1), всё происходит сразу на месте.
Что касается сложности по времени, то она зависит от просейки. Однократная просейка обходится в
Итоговая сложность по времени: O(n log n) + O(n log n) = O(n log n).
При этом у пирамидальной сортировки нет ни вырожденных ни лучших случаев. Любой массив будет обработан на приличной скорости, но при этом не будет ни деградации ни рекордов.
Сортировка кучей в среднем работает несколько медленнее чем быстрая сортировка. Но для quicksort можно подобрать массив-убийцу, на котором компьютер зависнет, а вот для heapsort — нет.
| Сложность по времени | |||
|---|---|---|---|
| Худшая | Средняя | Лучшая | |
| Сортировка кучей | O(n log n) | ||
| Быстрая сортировка | O(n2) | O(n log n) | O(n) |
Сортировка тернарной кучей :: Ternary heapsort
Давайте рассмотрим троичную кучу. От двоичной она, вы не поверите, отличается только тем, что у родительских узлов максимум не два, а три потомка. В тернарной куче для i-го элемента индексы его трёх потомков вычисляются аналогично (если у первого элемента индекс = 0):
Левый потомок: 3 × i + 1
Средний потомок: 3 × i + 2
Правый потомок: 3 × i + 3
(Если индексы начинать с 1, как на анимациях в этой статье, то в этих формулах надо просто отнять единицу).
Процесс сортировки:

С одной стороны заметно уменьшается количество уровней в дереве по сравнению с двоичной кучей, что означает, что в среднем при просейке будет происходить меньше свопов. С другой стороны, для нахождения минимального потомка понадобится больше сравнений — ведь потомков теперь не по два, а по три. В общем, в плане сложности по времени — где-то находим, где-то теряем, однако в целом тоже самое. Данные в тернарной куче сортируется немного быстрее чем в бинарной, но это убыстрение весьма незначительное. Во всех вариациях пирамидальной сортировки разработчики алгоритмов предпочитают брать именно двоичный вариант, потому что троичный якобы сложнее в реализации (хотя это «сложнее» заключается в добавлении в алгоритм буквально пары-тройки дополнительных строк), а выигрыш по скорости минимален.
Сортировка n-нарной кучей :: N-narny heapsort
Разумеется, можно не останавливаться на достигнутом и адаптировать сортировку кучей для любого числа потомков. Может быть, если и дальше увеличивать количества потомков, можно существенно повысить скорость процесса?
Для i-го элемента массива индексы (если отсчитывать их с нуля) его N потомков вычисляются очень просто:
1-й потомок: N × i + 1
2-й потомок: N × i + 2
3-й потомок: N × i + 3
…
N-й потомок: N × i + N
Код на Python сортировки N-нарной кучей:
# Основной алгоритм сортировки кучей для N потомков
def NHeapSort(data):
n = 3 # Сколько потомков у родителя
# Формируем первоначальное сортирующее дерево
# Для этого справа-налево перебираем элементы массива
# (у которых есть потомки) и делаем для каждого из них просейку
for start in range(len(data), -1, -1):
NHeapSift(data, n, start, len(data) - 1)
# Первый элемент массива всегда соответствует корню сортирующего дерева
# и поэтому является максимумом для неотсортированной части массива.
for end in range(len(data) - 1, 0, -1):
# Меняем этот максимум местами с последним
# элементом неотсортированной части массива
data[end], data[0] = data[0], data[end]
# После обмена в корне сортирующего дерева немаксимальный элемент
# Восстанавливаем сортирующее дерево
# Просейка для неотсортированной части массива
NHeapSift(data, n, 0, end - 1)
return data
# Просейка сверху-вниз для родителя у которого N потомков
def NHeapSift(data, n, start, end):
# Начало подмассива - узел, с которого начинаем просейку вниз
root = start
while True:
# Первого потомка (если он в пределах подмассива)
# назначаем максимальным потомком
child = root * n + 1
if child > end:
break
max = child
# Среди потомков определяем максимального
for k in range(2, n + 1):
current = root * n + k
if current > end:
break
if data[current] > data[max]:
max = current
# Если максимальный потомок больше родителя
# то меняем их местами и этот потомок сам
# становится родителем
if data[root] < data[max]:
data[root], data[max] = data[max], data[root]
root = max
else:
breakВпрочем, больше — не значит, лучше. Если довести ситуацию до предела и брать N потомков для массива из N элементов, то сортировка кучей деградирует до сортировки обычным выбором. Причём это будет ещё и ухудшенная версия сортировки выбором, так как будут совершаться бессмысленные телодвижения: просейка сначала будет ставить максимум на первое место в массиве, а потом будет отправлять максимум в конец (в selection sort отправка максимума в конец происходит сразу).
Если троичная куча минимально обгоняет двоичную, то четверичная уже проигрывает. Поиск максимального потомка среди нескольких становится слишком дорогим.
Трейлер следующей серии
Итак, основной недостаток бинарной/тернарной/n-нарной кучи — невозможность прыгнуть в своей сложности выше чем

Кликните по анимации для перехода в статью со следующей сортировкой кучей
Ссылки
Статьи серии:
- Excel-приложение AlgoLab.xlsm
- Сортировки обменами
- Сортировки вставками
- Сортировки выбором
- Сортировки слиянием
- Сортировки распределением
- Гибридные сортировки
В приложение AlgoLab добавлена сортировка n-нарной кучей. Чтобы выбрать количество потомков, в комментарии к ячейке этой сортировки нужно указать число для n. Диапазон возможных значений — от 2 до 5 (больше нет смысла, потому что при n >= 6 анимация уже при трёх уровнях вложенности при нормальном масштабе гарантировано не помещается на экране).
