
Сегодня много говорят о представлении музыки с помощью языков программирования, поскольку это, с одной стороны, интересная задача для инженеров, а с другой — является частью задачи универсального описания музыки.
Как это выглядит? Для многих языков созданы среды программирования музыки. Самые популярные — TidalCycles для Haskell и Sonic Pi для Ruby на Raspberry Pi. Есть также инструмент, использующий композиторскую библиотеку Leipzig. Поскольку он написан на языке Clojure, в нём отсутствует проверка типов.
(def row-row-row-your-boat
(phrase [3/3 3/3 2/3 1/3 3/3]
[ 0 0 0 1 2]))
->> row-row-row-your-boat
(canon (simple 4))
(where :pitch (comp C major))
(where :time (bpm 90))
play)
Длительность и высота звуков представлены в виде целых чисел и литералов-коэффициентов, что не слишком удобно. Когда речь заходит о музыкальных преобразованиях, программирование может стать прекрасным подспорьем. Скажем, в приведённом примере для аккомпанемента задается тональность до-мажор и темп 90 ударов в минуту.
Когда программисты видят музыкальный код, то чаще всего спрашивают, можно ли с помощью системы типов предотвратить фальшивое исполнение? Справедливый вопрос. Если музыку можно представить в виде кода, то можно ли считать ошибки при написании музыки ошибками программирования? И если да, то почему бы не улучшить процесс написания музыки с помощью методик, которые мы используем для написания программ?
В частности, есть очевидная аналогия между ошибками, которые может предотвратить система типов, и распространёнными случаями музыкальной неточности. Если ваш язык программирования умеет проверять, не передавали ли вы строку функции, которая ожидает получить число, то он сможет проверять, чтобы вы не использовали фа-диез в отрывке, написанном в тональности до-мажор, при ключе которой нет знаков альтерации.
В этой статье мы выясним, что делает музыку корректной и как это можно представить с помощью системы типов.
Прескриптивизм
Теоретики веками спорят о том, что делает музыку корректной. Чаще всего они действуют в рамках музыкального прескриптивизма: оценивая музыку на соответствие какому-то набору правил.
Можно так описать доминирующую методологию формирования правил:
- Изучение канона
- Определение закономерностей
- Формулирование их в виде набора правил
Тогда можно утверждать, что:
Музыка, не соответствующая этим правилам, является некорректной.
Например, правило композиции гласит, что не допускается в мелодии делать скачок на большую септиму от до до си. Этот подход привёл к многочисленным ценным находкам. В классической музыке существуют крайне интересные закономерности, и обобщение наших наблюдений в виде набора правил помогает в обсуждении феномена музыки.
Кроме того, следование правилам полезно при освоении музыкальных инструментов. Хорошо, когда учителя поправляют детей, которые практикуются играть на скрипке в до мажор, но сбиваются на фа диез. Есть ситуации, в которых полезно придерживаться определений корректной и некорректной музыки.
Однако у такого подхода есть два основных недостатка.
Во-первых, вытекающие из этого процесса правила сильно зависят от того, что теоретик считает каноном. Предвзятость датасета приводит к предвзятости выводов, и западная классическая музыка не отражает весь музыкальный опыт человечества. Создавать правила на основе музыки Баха и Моцарта может быть увлекательно, но они не слишком много расскажут о музыке в целом.
Ситуация осложняется, когда осознаёшь, что музыкальные жанры зачастую прочно ассоциируются с определёнными культурами и этническими группами, и что расставляя приоритеты определённым видам музыки вы тем самым невольно расставляете приоритеты определённым типам людей. Например, в академической теории музыки большое внимание уделяется изучению классических европейских традиций и относительно мало — музыке, берущей начало в диаспорах выходцев из Африки: блюзу, джазу, рок-н-роллу и хип-хопу. Если мы будем оценивать корректность музыки посредством традиционной теории, это может привести к культурологической версии проблемы, когда алгоритмы распознавания лиц лучше работали с европеоидами, чем с негроидами.
Вторым большим недостатком создания правил с помощью выявления и обобщения закономерностей является то, что таким образом мы всегда будем ориентироваться на прошлое. А музыка больше всего будоражит тогда, когда она нарушает правила. До того, как Джимми Пейдж использовал эффект дисторсии, инженеры считали клиппинг сигнала в ходе усиления дефектом. И пусть выявленные закономерности помогают понять современную музыку, однако они совершенно не годятся для оценки будущей музыки.
Хорошая система типов для музыки должна избегать обеих описанных ловушек прескриптивизма. В её основе не должно быть неприемлемых или субъективных критериев корректной музыки. При этом, стараясь сделать ошибочные состояния непредставимыми, система типов не должна мешать появлению новых состояний.
Дескриптивизм
Альтернативой прескриптивизму является дескриптивизм. Если в первом случае музыкальные закономерности рассматриваются как обязательные к исполнению правила, то во втором они рассматриваются как паттерны, формирующиеся в ходе практики. Дескриптивистский подход к исследованию музыкальных правил выглядит так:
- Исследуем тело музыки
- Выявляем тенденции
- Формулируем их в виде модели
Можно утверждать, что:
Музыка, отклоняющаяся от модели, является необычной.
Для этого нам нужна хорошая модель музыкальных структур, способная описать обычное или необычное, а не правильное или неправильное. Дэвид Хурон в своей книге Sweet Anticipation предлагает дескриптивистскую теорию, которую можно свести к трём ключевым аспектам:
- Музыка оценивается в ходе статистического обучения
- Вас радует правильный прогноз
- Новизна не позволяет вам заскучать
В нашем предыдущем прескриптивистском примере прыжок с ноты до на си считается ошибкой. А по теории Хурона это будет очень необычно. Те, кто много слушал западную музыку, узнают, что когда они слышат ноту до, то следующей нотой чаще всего будет другая до, либо нота на одну ступень выше или ниже по звучанию. Прыжок вверх на си удивит слушателей, и они могут отнестись к этому отрицательно.
Одним из любопытных следствий теории Хурона является то, что написание музыки — это не упражнение на максимальную или минимальную выдумку. Музыка балансирует на грани между порядком и хаосом, и расположение слушателей зависит от возможности музыканта сбалансировать шок новизны с удовлетворением от получения ожидаемого. Если вы действительно хотите проверить правильность композиции, то придётся убедиться, что она не слишком далеко отходит от принятых традиций, но и не соблюдает их слишком строго.
Ниже приведены данные статистического анализа мелодических тенденций. Тёмным цветом выделены более вероятные результаты. Выберите строку с одной из нот и найдите на ней ячейку с нотой, которая с большей вероятностью будет следовать за выбранной вами — выделенное тёмным цветом пересечение с колонкой другой ноты. Например, в этом датасете в 33,53 % случаев после ноты ре идёт нота до.
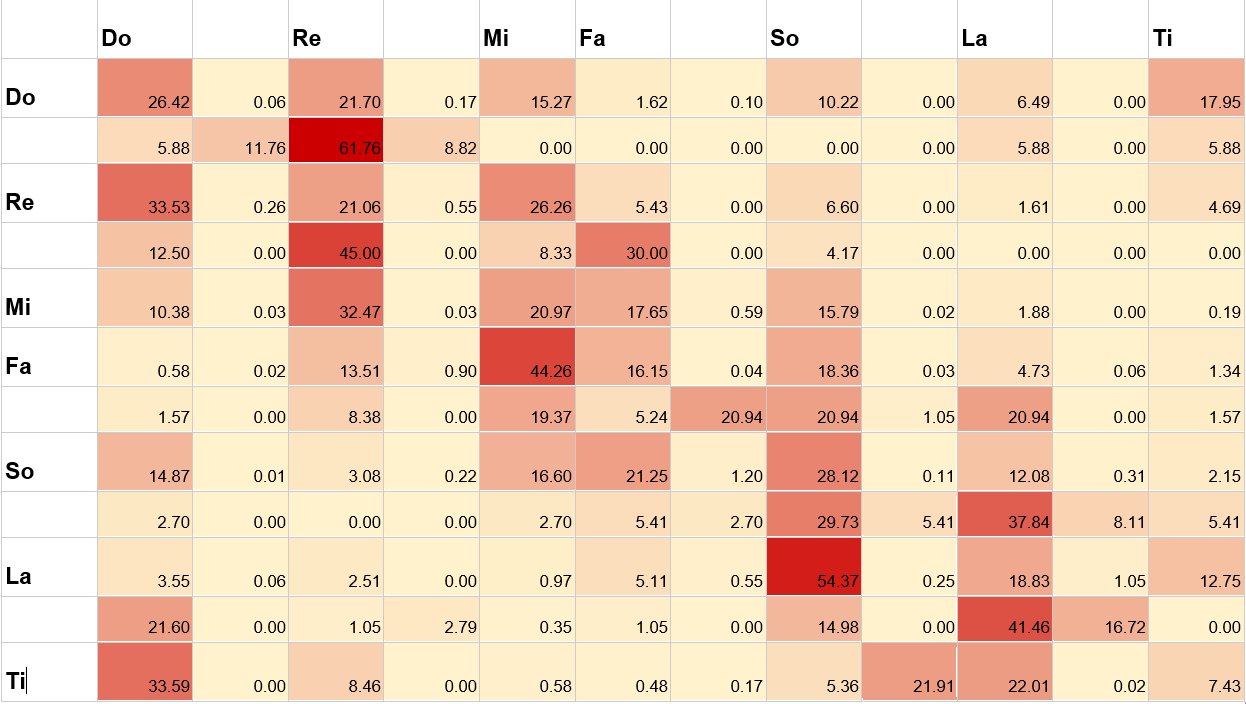
Эти данные взяты из книги Хурона, они являются результатом анализа более чем 250 000 тоновых пар из германских народных песен в мажоре. Другой массив данных, скажем, хип-хоп или рок-н-ролл продемонстрирует другие вероятности.
Все эти вероятности можно эквивалентно представить в виде битов энтропии: вероятность в 50 % соответствует одному биту, вероятность в 25 % — двум битам, и т.д. Чтобы избежать деления на ноль, будем считать, что у переходов, которые никогда не возникнут в датасете, вероятность равна 1/100 000. Теперь более тёмным цветом показаны переходы, которые обходятся дороже с точки зрения энтропии — то есть менее вероятные. Например, ля после ре равно 6 битам энтропии, то есть имеет вероятность 1/64.
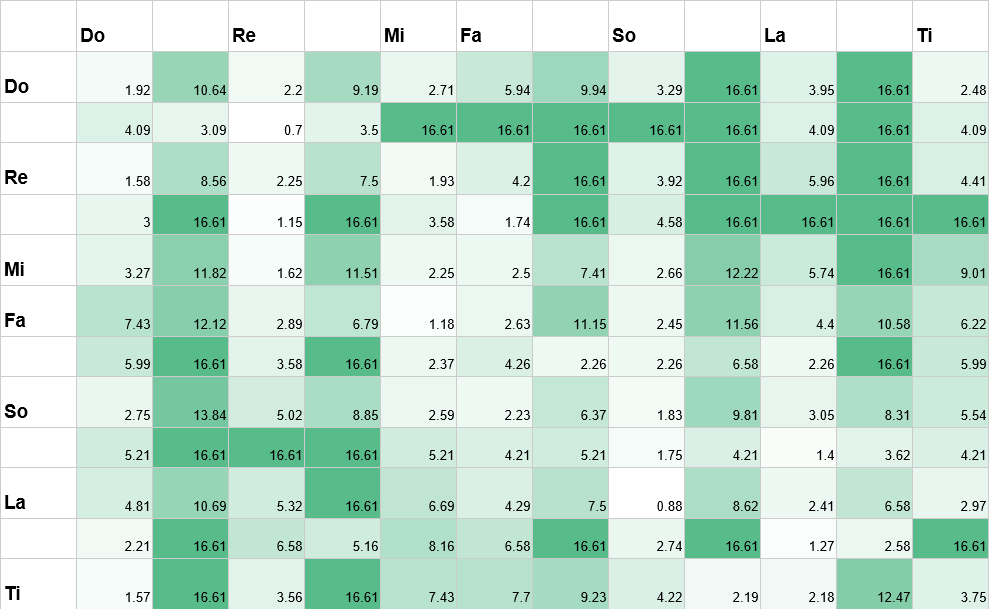
Представление в виде энтропии помогает нам объединить удивление от серии нот, в которой каждый переход от одного звука к другому является счётчиком энтропии, с удивлением от всей мелодии в виде суммы переходов.
до -> ре -> ми -> фа = 2,20 + 2,71 + 5,94 = 10,85 бит
до -> си -> ми -> фа = 2,48 + 7,43 + 5,94 = 15,85 бит
Это очень похоже на скрытую модель Маркова, только вместо генерирования строк нот мы для оценки вероятности появления мелодии используем весовые вероятности.
Вы могли заметить, что переход с ноты до на си равен всего 2,48 бит, хотя на первый взгляд это противоречит тому, что выше переход с до на си описывался как очень необычный. Чаще всего необычные переходы равны примерно 10 битам энтропии. Причина несоответствия в том, что в данных Хурона не делается различия между прыжком на шесть нот от до к си (очень необычно) и переходом на одну ноту от до к более низкой си (довольно частая ситуация). Если данные позволят разделять эти два случая, то модель покажет, что цепочка до — си — ми — фа будет звучать ещё более нетрадиционно, чем до — ре — ми — фа.
Типизированные ноты
В идеале система типов помогает программистам принимать правильные решения и исключает возможность ошибок. Хорошая музыкальная аналогия — сольфеджио. Если у вас нет музыкального образования, то вы могли познакомиться с сольфеджио по песенке Do-Re-Mi из мюзикла The Sound of Music. У каждой ноты октавы есть своё название, а любая нота вне тональности названия не имеет:
- До (самая низкая нота из этого набора)
- Ре
- Ми
- Фа
- Соль
- Ля
- Си
- До (теперь октавой выше)
Эта система позволяет музыкантам придерживаться правильных нот, она задаёт миниязык, запрещающий воспроизводить ноты вне выбранного ключа. Существует бесконечно много частот между до и ре, но в рамках сольфеджио они не воспроизводятся.
Это можно легко представить в коде в виде данных алгебраического типа:
data Solfege = Do | Re | Mi | Fa | So | La | Ti
Теперь можно определить музыкальные функции, которые не допускают нот вне ключей. Например, эта функция повторяет одну ноту n раз:
repeat : Nat -> Solfege -> List Solfege
repeat 0 s = [s]
repeat n s = s :: repeat (n - 1) s
При таком определении трёхкратный повтор ноты ре — это выражение, которое будет легко понято в музыкальной сфере. А трёхкратное повторение фа диез — это ошибка проверки типа, потому что фа диез не является значением типа
Solfege.Это даёт нам определённую типобезопасность. Наша система позволяет нам избежать неправильных нот, но она ещё не защищает от неправильных комбинаций нот. Если бы мы играли в тональности до-мажор, то не стали бы играть фа диез, однако могли бы сыграть до, затем прыгнуть на большую септиму на ноту си, что запрещается (традиционными) правилами композиции. Такая контекстуальная проверка типов возможна, но требует более сложного подхода.
Типизированные переходы
Haskell-библиотека Mezzo для проверки музыкальной корректности использует связанные типы. В описании говорится, что это «очень строгая проверка для музыки», библиотека может проверять на соответствие различным правилам композиции, а не только тональности. В Mezzo следующий код скомпилируется потому, что мелодия до — ре — ми — фа состоит из разрешённых интервалов:
comp = defScore $ start $ melody :| c :| d :| e :| f :>> g
Но если мы нарушим правило, запрещающее прыгать с до на си, то Mezzo такой код не скомпилирует:
comp = defScore $ start $ melody :| c :| b :| e :| f :>> g
Замечательно, что Mezzo даже укажет на проблему:
Major sevenths are not permitted in melody: C and B
In the first argument of ‘(:|)’, namely ‘melody :| c :| b’
In the first argument of ‘(:|)’, namely ‘melody :| c :| b :| e’
In the first argument of ‘(:>>)’, namely
‘melody :| c :| b :| e :| f_’
Может показаться, что сбылась мечта представления некорректной музыки как ошибки типов. Но иногда возникают неловкие ситуации. Когда автор библиотеки закодировал прелюдию Шопена, то выяснилось, что несколько раз композитор не соблюдал традиционные правила:
Произведение транскрибировалось почти целиком, но иногда приходилось пропускать несколько нот, потому что они создавали запрещённые интервалы, на которые указывала Mezzo.
Вы можете спросить, кто это взялся запрещать? Если уж Шопену не позволяется говорить о том, что допустимо в западной музыке, а что нет, то кому тогда?
Проблема в том, что хотя Mezzo и способна учесть контекст, однако оценка типов остаётся задачей двоичного выбора. Либо все ноты верны и произведение компилируется, ли одна из нот выбивается и произведение не компилируется. И несмотря на то, что Mezzo позволяет выбирать правила композиции, решение о применении или неприменении правила является глобальным. Если вы отключите правило, потому что какое-то музыкальное решение нарушает обычное соглашение, то вы отмените проверку других частей произведения.
Типизированная энтропия
Один из способов нарушения или обхода музыкальных правил типизации заключается в том, чтобы по совету Хурона смоделировать переходы между нотами с точки зрения похожести. Вместо того, чтобы объявлять конкретный переход правильным или неправильным, можно подсчитать количество энтропии, которое отражает удивление слушателей от парных сочетаний нот.
Следующий код написан на зависимо-типизированном функциональном языке Idris. В коде проверяется, чтобы соответствующая правилам мелодия начиналась с до и заканчивалась на соль и чтобы путь между этими нотами генерировал 8-16 бит энтропии. Сначала нужно определить тип
Melody, который отражает наше представление мелодии с определённой схожестью или величиной энтропии. У этого типа три конструктора:Pure: отражает создание мелодии из одной ноты, с верхней и нижним уровнем энтропии, равными нулю.(>>=): берёт две мелодии и складывает их границы энтропии со стоимостью перехода от ноты в конце первой мелодии к ноте к в конце второй.Relax: берёт мелодию и расширяет её границы энтропии.
data Melody : (Solfege, Solfege) -> (Nat, Nat) -> Type where
Pure : x -> Melody (x, x) (0, 0)
(>>=) : Melody (w, x) (low, high) ->
(() -> Melody (y, z) (low2, high2)) ->
Melody (w, z) (cost x y + low + low2, cost x y + high + high2)
Relax : Melody (x, y) (low + dl, high) ->
Melody (x, y) (low, high + dh)
Такое определение типа сложнее, но благодаря ему в Idris можно составлять мелодию с помощью нотации
do, и компилятор отследит для нас границы энтропии. Вот соответствующая правилам мелодия с низкой стоимостью всех переходов:conventional : Melody (Do, So) (8, 16)
conventional = Relax $ do
Pure Do
Pure Re
Pure Mi
Pure Fa
Pure So
Следующая мелодия не соответствует правилам, потому что в ней совершается прыжок на большую септиму. В Mezzo она будет либо запрещена, либо придётся совсем отключить правило. Здесь мы всего лишь расширили границы сложности мелодии, чтобы она укладывалась в диапазон 8-24 бита энтропии:
unconventional : Melody (Do, So) (8, 24)
unconventional = Relax $ do
Pure Do
Pure Ti
Pure Mi
Pure Fa
Pure So
Если вместо
Melody (Do, So) (8, 24) мы присвоили бы не соответствующей правилам мелодии тип Melody (Do, So) (8, 16), то она не скомпилировалась бы!Новизна подхода в том, что он позволяет понять, когда музыка становится слишком скучной. Если энтропия мелодии не достигает нижней границы, генерируется ошибка типа. Так что если мелодии, соответствующей правилам, присвоить тип
Melody (Do, So) (16, 24), то она тоже не будет скомпилирована, потому что её энтропия не достигает нижней границы. Это внушает нам веру в теорию Хурона, согласно которой людям будет слишком тяжело слушать музыку, которая излишне необычна или непредсказуема.В вырожденном случае переходы между нотами внутри тональности не увеличивают энтропию, а переходы вне тональности дают произвольно большой прирост энтропии. Тогда целесообразно вновь обратиться к двоичной оценке, при которой каждая нота будет считаться разрешённой или запрещённой, безо всяких промежуточных статусов.
Важно, но трудно проверить
Проверять типы в музыке сложно, потому что трудно определить корректность музыки. Если мы не можем математически точно смоделировать определение музыкальной корректности, то мы не можем перенести её в систему типов. Даже если удастся аутентично формализовать наше понимание, то потребуется приложить усилия и применить мощную систему типов, чтобы компилятор смог адекватно оценивать мелодию. Впрочем, это возможно при наличии какого-то определения и нескольких упрощающих предположениях.
Это всего лишь любопытство? Возможно. Вряд ли музыкальная индустрия в скором времени возьмёт на вооружение систему типов, чтобы предотвращать композиторские ошибки. Но если исследование вычислений в сфере музыки поможет нам иначе оценить то, что играет такую важную роль в жизни почти каждого из нас, то уже само это оправдывает все усилия.
Пожалуй, не менее важно и то, что музыка — лишь одна из сфер, где корректность проверять важно, но трудно. Чем активнее с помощью программирования автоматизируют социальную и культурную сферу, тем чаще возникают ситуации, в которых трудно оценить ответ, имеющий для людей решающее значение. Возьмите использование компьютерной программы, которая решает, на какой срок сажать в тюрьму. Корректность выносимых приговоров зависит от сложных компромиссов между затратами и вероятностями, и если мы не сможем отслеживать логику принятия решений системой, то как мы сможем оценить справедливость результата?
Каждый раз, когда мы автоматизируем непрозрачные процессы принятия решений, нужно спрашивать себя: «А как мы узнаем, что система работает корректно?».