Что если бы я вам сказал, что без понимания что такое backpropagation (обратное распространение ошибки) вы никогда не сможете использовать AI эффективно? Тогда я бы, конечно, соврал. Знать такие детали не требуется для использования AI в прикладных задачах, но, тем не менее, это базовый фундамент ML/AI и понимать как все устроенно - полезно, ну или как минимум, интересно.
Впервые этот метод был описан в 1960-е но популярным стал после описания его в 1986 году в статье под названием «Learning representations by back-propagating errors».
Перед обсуждением обратного распространения ошибки давайте рассмотрим, что такое нейронная сеть? Концептуально — что она делает — она пытается преобразовать ряд входных данных (например, изображения) в ряд выходных данных (ответы на вопросы, например, есть ли на этих картинках собаки) посредством процесса трансформации этих изображений, пропуская их через сеть нейронов. Изображения — это просто массивы байтов, так как это происходит?
Если подумать, байты представляют числа (или, точнее, цвета каждого пикселя, что также является числом). Так что нам нужно преобразовать массив чисел в ответ на вопрос: "Это собака?".
В простом случае, допустим, мы знаем, что у нас есть только два типа изображений — полностью белое пустое изображение и изображение с собакой. В этом случае, если мы видим хотя бы один небелый пиксель на изображении — мы можем с уверенностью сказать, что это собака. Это самая простая нейронная сеть, которую можно представить в виде выражения:
isADog = isNonZero( sum ( abs(pixel_color_value - white_color_value ) ) )Это означает, что если каждый пиксель имеет белый цвет — разница pixel_color_value - white_color_value (это по сути константа 0xFFFFFF) будет нулевой, а сумма всех пикселей также будет нулевой и, следовательно, изображение пустое.
Таким образом, нейрон имеет следующее:
Inputs (пиксели)
Weights and biases (константа white_color_value в данном случае bias, или смещение)
ReLUs функции активации (isNonZero в нашем случае)
Output(s) (вывод)
Входные данные передаются в сеть, и её топология (количество нейронов, как они связаны и функции активации) фиксированы и не изменяются после создания сети. Так что же изменяется во время обучения? Только веса и смещения. Это параметры сети, которые в процессе обучения будут изменяться, чтобы сеть выполняла что-то полезное. Таким образом, сеть состоит из:
Её нейронов (или слоев нейронов) и их связей, которые фиксированы
Весов - которые могут быть изменены во время тренировки
Нейрон внутри просто вычисляет взвешенную сумму своих входных данных, прибавляя к ней параметр, который называется bias. Ключевое слово здесь - "взвешенная" сумма. Он умножает все входные данные на определенный параметр, называемый весом. Как мы обсудили в этой статье, веса вычисляются в процессе обучения, и это главная цель обучения. Таким образом веса и bias, в целом, это магические числа, полученные эмпирическим путем (он же метод тыка) в процессе обучения. Вот что он делает:
output = activation_function( sum(weight * inputs + bias) )
Cеть же – это просто много нейронов, соединенных вместе:
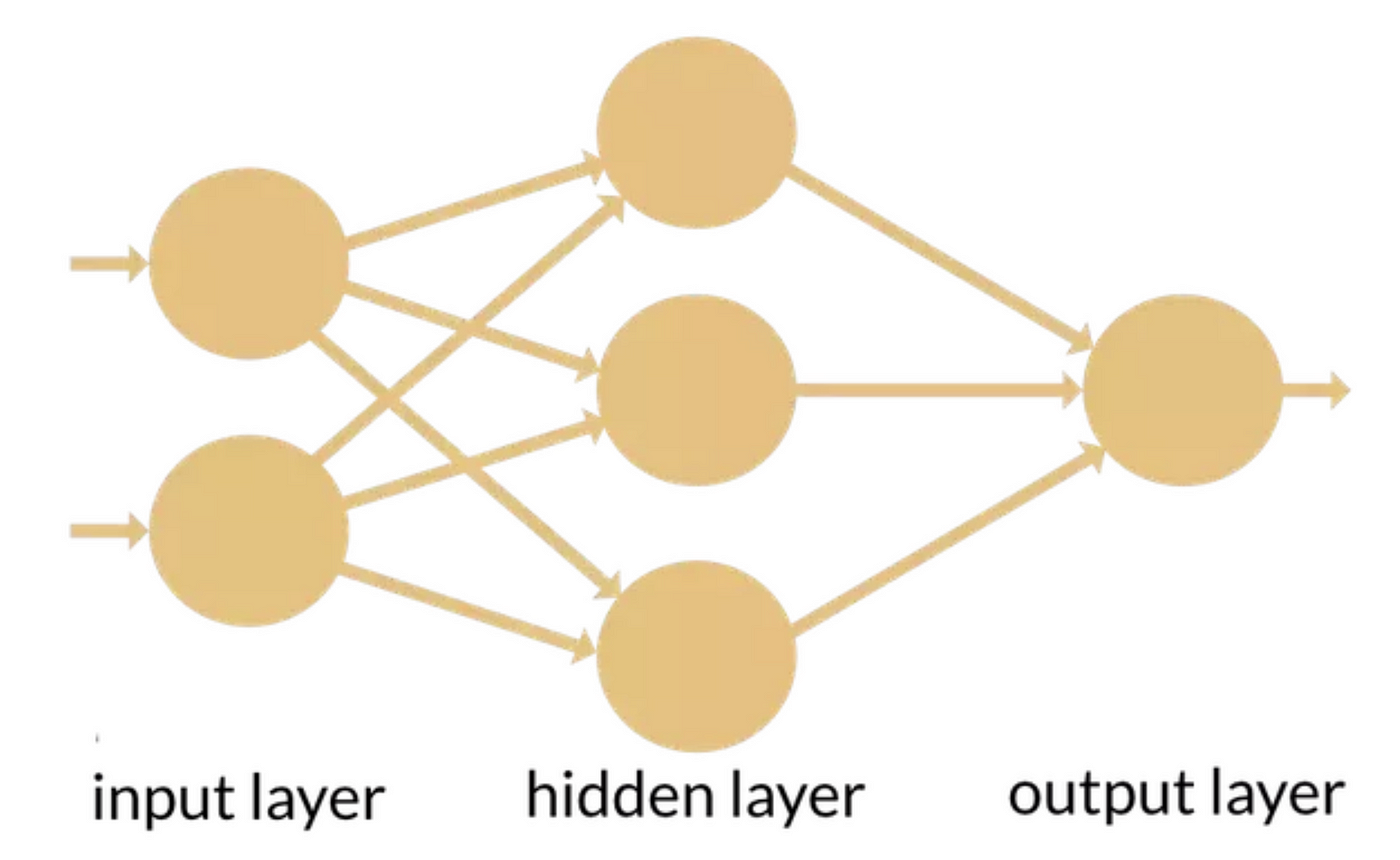
Обратное распространение ошибок (backpropagation) — это процесс, используемый для обновления весов сети во время обучения.
Обучение обычно проходит так: у нас есть обучающий набор данных, который уже правильно помечен. Представим, что у нас есть куча изображений собак, которые мы пометили что это собаки, и куча случайных изображений, которые мы пометили как не собаки.
Мы подаем изображение в сеть одно за другим (прямой проход), и если оно угадано неправильно — немного изменяем веса (обратный проход). Мы делаем это тысячи раз и, в конце концов, находим комбинацию весов, которая лучше всего определяет собак.
Звучит просто, но как мы знаем, как изменить веса? Здесь мы используем обратное распространение ошибок.
Прежде всего, на каждом таком шаге мы рассчитываем ошибку (loss), которые по сути являются ошибкой для данного входа (изображения) и обычно представляют собой разницу между рассчитанным значением и ожидаемым значением. Предположим, наша сеть предположила, что изображение на 57% вероятно является собакой. А изображение на самом деле кот (то есть вероятность равна 0), так что ошибка или потеря составляет abs(0 - 0.57) = 0.57. Если использовать среднеквадратичную ошибку то получим (0 - 0.57)^2 = 0.32.
Я упрощаю, но идея такова. Чтобы улучшить нашу сеть, нам нужно немного изменить веса, чтобы потери уменьшились. Если мы можем изменить веса так, что теперь она предсказывает только 55% вероятность, мы улучшились на 2% и движемся в правильном направлении.
Идея обратного распространения заключается в том, чтобы распространять ошибку (потери) в обратном направлении после того, как мы её рассчитали, изменяя веса таким образом, чтобы ошибка немного уменьшилась. Не значительно, а немного (я объясню почему позже) — и делать это итеративно, пока потери не станут приемлемыми.
Мы меняем веса, увеличивая или уменьшая их, так как они являются просто числами. Откуда мы знаем, следует ли увеличивать или уменьшать и на сколько? Это два очень хороших вопроса, детектив. Никакой магии тут нет, но есть вещь, которая для многих пострашнее черной магии - математика 7го класса.
Давайте сначала посмотрим, следует ли увеличивать или уменьшать.
Мы собираемся использовать то, что называется методом градиентного спуска. Зависимость ошибки от весов можно записать как:
loss = loss_function( NN (inputs, weights), expected_output)
или, другими словами, нам нужно посчитать производную:
derivative = d_loss/d_weightгде NN — это наша нейронная сеть, а loss_function — это функция, которую мы используем для расчета потерь (может быть просто средним или среднеквадратичной функцией).
Используя метод градиентного спуска, мы определяем направление изменения весов на основе градиента функции потерь. Градиент (угол наклона) показывает направление наибольшего увеличения функции, поэтому, чтобы уменьшить потери, мы движемся в противоположном направлении.
Градиент функции потерь по отношению к весам показывает, как небольшое изменение веса влияет на потери. Если производная положительна, увеличение веса приведет к увеличению потерь, и мы должны уменьшить вес. Если производная отрицательна, увеличение веса уменьшит потери, и мы должны увеличить вес.
На практике мы обновляем веса с использованием следующего правила обновления:

Это позволяет нам итеративно корректировать веса в направлении, которое уменьшает потери, постепенно приближаясь к оптимальным значениям весов для нашей модели.
Давайте вспомним школу и, что такое производная:
Производная — это показатель скорости изменения одной переменной относительно другой. В контексте обучения нейронных сетей, производная функции потерь по весам показывает, как изменение весов влияет на изменение значения потерь — именно то, что нам нужно для корректировки весов.
Скорость изменения: c геометрической точки зрения, производная показывает, насколько "крут" график функции в любой данной точке. Большое абсолютное значение производной указывает на крутой наклон (быстрый рост или быстрое падение функции), а малое абсолютное значение производной указывает на малый наклон (плавный рост или падение функции).
Положительный или отрицательный наклон: если производная в точке положительна, это означает, что функция возрастает в этой точке, и наклон касательной линии направлен вверх. Если производная отрицательна, функция убывает, и наклон касательной линии направлен вниз.
Нулевая производная: когда производная в точке равна нулю, это означает, что наклон касательной линии горизонтален. Такие точки могут быть локальными максимумами, локальными минимумами или точками перегиба функции, где поведение функции изменяется с возрастания на убывание или наоборот.
Для нейронной сети производная будет вычисляться как производная всех функций, присущих слоям нейронов. Предположим, у нас есть два слоя (входной и выходной), тогда у нас будут следующие функции (в обратном порядке):
f_loss (f_out, expected) – функция потерь, которая принимает результаты выходного слоя и ожидаемое значение для расчета потерь, например, среднеквадратичная ошибка (но может быть и любой другой).
f_out (f_relu_in, weight_out) – функция выходного слоя, которая зависит от весов и смещений выходного слоя и ее входа, который есть результат функции активации входного слоя.
f_relu_in (f_in) – функция активации входного слоя, зависящая от функции входного слоя.
f_in (inputs_in, weights_in) – функция входного слоя, зависящая от начальных входов и весов входного слоя.
Расчет производной, где одна функция зависит от предыдущей, может выглядеть сложно, но на самом деле это не так благодаря правилу цепочки для производных. Оно гласит: производная от f(g(x)) равна f'(g(x))⋅g'(x), или производная цепочки функций равна произведению их производных, другими словами, мы можем вычислить производные для каждой функции и умножить их друг на друга.
После того как производные всей цепочки вычислены, мы умножаем их на небольшой коэфициент, называемое скоростью обучения (learning rate), и используем это для изменения весов на полученный результат и повторяем этот процесс до тех пор, пока ошибка (loss) при текущих весах не окажется в приемлемом диапазоне.
Вы можете спросить — зачем нужна скорость обучения? Это очень хороший вопрос. Причина в том, что нам нужно двигаться медленно — чтобы мы могли наблюдать, как влияют изменения, которые мы вносим, на потери. Если мы начнем двигаться слишком быстро, мы можем перескочить минимум функции потерь, который пытаемся найти с помощью градиентного спуска. При больших шагах легко перескочить минимум, и тогда алгоритм может попасть в бесконечный цикл, прыгая вокруг минимума, но не способный сойтись из-за размера шага.
Скорость обучения, таким образом, контролирует размер шага в процессе градиентного спуска. Слишком большая скорость обучения может привести к тому, что алгоритм будет прыгать через минимум, не улавливая его, а слишком маленькая скорость обучения сделает процесс обучения слишком медленным и неэффективным, потенциально затягивая сходимость.
Идеально подобранная скорость обучения позволяет сети эффективно минимизировать потери, делая достаточно малые шаги для точного приближения к минимуму, но достаточно большие, чтобы процесс не затягивался на долгое время. Это баланс между скоростью и точностью сходимости, который необходимо тщательно настраивать в процессе обучения нейронных сетей. Обычно подбирается эмпирически.

Таким образом, обратное распространение — это вычисление производной сложной функции, которое по сути отражает, как изменяется потеря (ошибка), когда мы слегка изменяем веса, а затем изменение весов в направлении уменьшения потерь маленькими шагами. Этот процесс итеративен и продолжается до тех пор, пока ошибка не станет приемлемой.
Если вы хотите узнать больше о градиентном спуске, вот отдельная статья по этой теме.
Я со-основатель AI интегратора Рафт. Мой телеграм-канал.
Всем хорошего дня!