Comments 30
Пункты © и (D) наводят на мысли о переполнении числового типа во Вселенной.
В примере (С) определяется a[n_] := Cos[n+1], а затем используется s[n].
UFO just landed and posted this here
Мне вот что интересно. Да, они применили определённый «чит» и получили конечный ответ там, где по идее должна быть бесконечность. Имеют формальное право. Но почему разными читами получается один и тот же ответ? Можно ли придумать другой способ, в результате которого получится другой ответ? Если да, то значение -1/12, по идее, не имеет никакой ценности.
В математике много «читов», многие из них очень интересные. Взять хоть условно сходящиеся ряды… их сумму можно сделать любой наперед заданной, просто меняя порядок членов в сумме, о чем есть соответствующая теорема. Это все игры с бесконечностью, из-за них получается много неочевидных результатов.
Теорема Римана это прекрасно, да, но там всё же дело с условно сходящимися рядами, а не с расходящимися. И можете ли Вы ответить на мой вопрос?
Проблема здесь в том, что вы должны придумать такую регуляризацию, чтобы для сходящихся рядов она давала тоже самое значение, причем для разных регуляризаций тоже. Мой интуитивный ответ — нет. Скажем, если вы возьмете первый ряд и вычислите его суммы по всем методам вы везде получите -1/2.
UFO just landed and posted this here
Есть такая штука, называется обобщённое суммирование.
Изначально у нас есть 3 аксиомы сложения конечного числа слагаемых: ассоциативность, коммутативность и дистрибутивность (линейность). С первыми двумя появляются проблемы, если мы хотим разрешить менять местами бесконечное число слагаемых (перестановкой членов можно заставить условно сходящийся ряд сходиться к любому числу) или расставлять бесконечное число скобок ( 1+(−1+1)+...=1, в то время как (1−1)+(1−1)+...=0). Поэтому мы говорим, что от бесконечной суммы мы хотим две вещи:
1. Чтобы она была похожа на сумму
.
2. И чтобы она была линейна
.
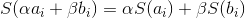После этого для большинства расходящихся рядов можно сумму посчитать. Причём сумма не будет зависеть от метода суммирования (по Борелю, по Чезаро, по Эйлеру или ещё как), если метод по сути удовлетворяет двум вышеназванным свойствам.
Можно даже вместо регуляризации делать такие фокусы:
Изначально у нас есть 3 аксиомы сложения конечного числа слагаемых: ассоциативность, коммутативность и дистрибутивность (линейность). С первыми двумя появляются проблемы, если мы хотим разрешить менять местами бесконечное число слагаемых (перестановкой членов можно заставить условно сходящийся ряд сходиться к любому числу) или расставлять бесконечное число скобок ( 1+(−1+1)+...=1, в то время как (1−1)+(1−1)+...=0). Поэтому мы говорим, что от бесконечной суммы мы хотим две вещи:
1. Чтобы она была похожа на сумму
.2. И чтобы она была линейна
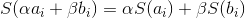.После этого для большинства расходящихся рядов можно сумму посчитать. Причём сумма не будет зависеть от метода суммирования (по Борелю, по Чезаро, по Эйлеру или ещё как), если метод по сути удовлетворяет двум вышеназванным свойствам.
Можно даже вместо регуляризации делать такие фокусы:
UFO just landed and posted this here
Позволю не согласиться, что выбор чита — это всегда строгая процедура. Потребности физики часто были на шаг впереди строгости математики. Сначала Ньютон с Лейбницем придумали интегрально-дифференциальное исчисление, спустя век появилось строгое обоснование от Римана, а потом Лебега. Сначала Дирак вовсю использовал дельта-функции, потом математики создали теорию обобщённых функций. Таких примеров масса. Зачастую математическая интуиция полезнее строгости, хотя чем дальше в лес, тем больше контр-интуитивных для простого человека ситуаций встречается.
Можно получить 5/12.
Запишем наш ряд 4 способами:
S1=1+2+3+4+5+6+7+8+…
S2=1+0+2+0+3+0+4+0+…
S3=0+1+2+3+4+5+6+7+…
S4=0+0+1+0+2+0+3+0+…
Видно, что S1=S2=S3=S4=S — искомая сумма.
Вычислим -3*S=3*S1-6*S2-2*S3+S4. Получится:
-3*S=-3+4-5+6-7+8…
Дважды сложим этот ряд с ним же, сдвинутым на одно слагаемое:
-6*S=-3+1-1+1-1+1-…
-12*S=-3-2+0+0+0+0+...=-5
Отсюда S=5/12.
Запишем наш ряд 4 способами:
S1=1+2+3+4+5+6+7+8+…
S2=1+0+2+0+3+0+4+0+…
S3=0+1+2+3+4+5+6+7+…
S4=0+0+1+0+2+0+3+0+…
Видно, что S1=S2=S3=S4=S — искомая сумма.
Вычислим -3*S=3*S1-6*S2-2*S3+S4. Получится:
-3*S=-3+4-5+6-7+8…
Дважды сложим этот ряд с ним же, сдвинутым на одно слагаемое:
-6*S=-3+1-1+1-1+1-…
-12*S=-3-2+0+0+0+0+...=-5
Отсюда S=5/12.
Вы вставили во второй и четвёртый ряд бесконечное число нулей. Не надо так =)
Два условия из определения обобщённой суммы разрешают нам
1) добавить/убрать/переставить конечное количество слагаемых
2) сложить несколько рядов почленно (с возможным домножением на множители)
Когда мы «всунули» в ряд бесконечное число нулей, мы его разрядили и его сумма изменилась, S1 не равно S2. Понятие бесконечности качественно отличается от любого сколь угодно большого числа. Иногда бесконечные суммы можно рассматривать как предел частичных конечных сумм, а иногда все частичные суммы положительные, а сумма ряда отрицательная.
Два условия из определения обобщённой суммы разрешают нам
1) добавить/убрать/переставить конечное количество слагаемых
2) сложить несколько рядов почленно (с возможным домножением на множители)
Когда мы «всунули» в ряд бесконечное число нулей, мы его разрядили и его сумма изменилась, S1 не равно S2. Понятие бесконечности качественно отличается от любого сколь угодно большого числа. Иногда бесконечные суммы можно рассматривать как предел частичных конечных сумм, а иногда все частичные суммы положительные, а сумма ряда отрицательная.
Вы вставили во второй и четвёртый ряд бесконечное число нулей. Не надо так =)
В общем случае — возможно. Но возьмите рассуждение из Вашего собственного комментария. Когда мы вычитаем из ряда s3=1+2+3+4+… ряд s2=1-2+3-4+..., то получаем s3-s2=4*(0+1+0+2+...). Сумму этого ряда приравняли к 4*s3, и получили общепринятый корректный результат. Отсюда можно сделать вывод, что в данном конкретном случае 1+2+3+4+...=0+1+0+2+0+3+..., т.е. в моих терминах S1=S2. Дальше — работа с конечным числом нулей и линейными комбинациями.
На самом деле, разрешение вставить конечное число нулей и вычислить линейную комбинацию не даёт даже найти S=1+1+1+1+…
В самом деле, вставив ноль в начале, получим S=0+1+1+1+..., а вычтя один ряд из другого, получим 0=S-S=1+0+0+0+...=1.
Похоже, что здесь важна нумерация членов ряда — например, с нулевого члена мы его суммируем, или с первого; какой будет производящая функция — 1/(1-x) или x/(1-x), и т.п.
В самом деле, вставив ноль в начале, получим S=0+1+1+1+..., а вычтя один ряд из другого, получим 0=S-S=1+0+0+0+...=1.
Похоже, что здесь важна нумерация членов ряда — например, с нулевого члена мы его суммируем, или с первого; какой будет производящая функция — 1/(1-x) или x/(1-x), и т.п.
UFO just landed and posted this here
Да, каюсь, я вас обманул с последним фокусом. Простите меня. Обобщённой суммы натуральных чисел, по-видимому, не существует. Для этого нужно использовать нелинейные регуляризации типа Дирихле.
В оправдание поясню, почему ответ в моём фокусе совпадает, например, с регуляризацией через экспоненциальный ряд. (Эта регуляризация уже не обладает стабильностью, но, по крайней мере, линейна, т.е. мы можем складывать ряды). Теперь нам действительно важно какое число будет первым: S(1,2,3...) ≠ S(0,1,2...). Но если мы разрядим ряд таким образом: a_n = 0, 1, 0, 2, 0, 3..., то его сумма не изменится:
Таким образом, для данного типа регуляризации допустимо складывание рядов и подобное разрежение без сдвига, поэтому ответ получается «верным». Но я согласен, что зря влепил последний пример в обобщённые суммы.
Что касается суммирования по Борелю, то оно, очевидно, обладает свойствами линейности. Для доказательства стабильности рассмотрим произвольный ряд a_k, добавим к нему в начало произвольный элемент a_0 и возьмём интеграл Бореля по частям:
Так что похоже, что регуляризация по Борелю всё-таки стабильна.
В оправдание поясню, почему ответ в моём фокусе совпадает, например, с регуляризацией через экспоненциальный ряд. (Эта регуляризация уже не обладает стабильностью, но, по крайней мере, линейна, т.е. мы можем складывать ряды). Теперь нам действительно важно какое число будет первым: S(1,2,3...) ≠ S(0,1,2...). Но если мы разрядим ряд таким образом: a_n = 0, 1, 0, 2, 0, 3..., то его сумма не изменится:
Таким образом, для данного типа регуляризации допустимо складывание рядов и подобное разрежение без сдвига, поэтому ответ получается «верным». Но я согласен, что зря влепил последний пример в обобщённые суммы.
Что касается суммирования по Борелю, то оно, очевидно, обладает свойствами линейности. Для доказательства стабильности рассмотрим произвольный ряд a_k, добавим к нему в начало произвольный элемент a_0 и возьмём интеграл Бореля по частям:
Так что похоже, что регуляризация по Борелю всё-таки стабильна.
Что-то тут не так: 3*S1-6*S2-2*S3+S4 не равно -3S, видимо должно быть 3*S1-6*S2-2*S3+2*S4, тогда дальнейшие арифметические результаты, вроде бы, верны. Кроме того, приравнивать нулю сумму ряда 1-1+1-1+… мне кажется несколько опрометчивым :)
Не могу удержаться.
В магазин заходит бесконечное число математиков. Первый просит килограмм картошки, второй — полкило, третий — четверть… «Понял,» — говорит продавец и кладет на прилавок два килограмма.
Кстати, (D) в частности используется, чтобы найти критическую размерность пространства-времени в бозонной теории струн.
Sign up to leave a comment.
Суммирование расходящихся рядов методами Абеля, Бореля, Чезаро и Дирихле