
Рассматривая различные существующие способы к построению пользовательских интерфейсов, меня вдруг посетила мысль, что возможно выбран в принципе неверный путь. Вновь людьми выбрана «квадратная» модель отображения информации, как и почти во всех других областях своей деятельности. Я не призываю к революции в построении пользовательских интерфейсов, но возможно мысли о фракталах многие найдут интересными.
На протяжении тысячелетий люди создают различные рукотворные объекты, оперируя всего несколькими простейшими геометрическими фигурами и их комбинациями. Основными объектами стали: прямоугольник, круг, треугольник, и их трехмерные аналоги — параллелепипед, шар, пирамида. Примеры можно приводить бесконечно. но проще всего посмотреть на постройки, которые нас окружают. Начиная от элементов из которых мы создаем здания:

И кончая самими постройками:

Пожалуй нашу цивилизацию вполне можно назвать «квадратной», или по желанию «прямоугольной». Так сложилось за тысячи лет развития общества и видимо продлится, если не вечно, то еще многие сотни или тысячи лет. Но выбранные человеком базовые формы далеко не идеальны и природа оперирует совсем другим классом объектов — фракталами.

Фрактал — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба.

Фрактальная форма оптимальна для живых объектов и мы можем встретить ее повсеместна. Человек открыл это великолепие форм совсем недавно. С момента публикации работы «Фрактальная геометрия природы» Бенуа Мандельброта в 1977 году прошло всего несколько десятков лет. Миг в сравнении культурных эпох человека. И не удивительно, что человек делает только маленькие шаги, пытаясь освоить те возможности, которая дает ему математика фракталов и новые геометрические формы.
Например, фрактальное устройства антенны, позволяет ей принимать широкий спектр частот, и мы активно используем эту фрактальность в сотовых телефонах.

А теперь я хочу робко намекнуть на идею, о возможности использования фракталов в нашем с вами общении с компьютером. В представлении информации и графических интерфейсах. Я не готов высказать законченную идею, но возможно кого-то подготовлю к этому. :)
Графические интерфейсы множества приложений безобразны, если взглянуть на них строго. Они неудобны, заставляя глаза скользить по рядам кнопок, выискивая нужный элемент. Они ужасно выглядят при смене разрешений, размеров шрифтов. При чем я говорю не сколько о ошибках в программах, описанных мною здесь, а о принципиальной сложности создать программу, которая может адекватно отобразить себя на различных устройствах. Это проблема растет с ростом популярности различны портативных устройств — ноутбуков, телефонов, цифровых фотоаппаратов.
Чтобы одна программа могла по настоящему красиво выглядеть на разных гаджетах, ее интерфейс нужно каждый раз модифицировать под конкретное устройство. Где-то расположить по-другому элементу, где-то убрать неосновные кнопки. И все это связанно с вновь выбранной идеологией «квадратности». Ведь если присмотреться, то интерфейс типовой программы состоит их квадратных элементов:
И даже если используются круги или эллипсы, то это мало влияет на суть. Это просто украшения, а вовсе не новый подход к созданию интерфейсов.
А теперь перейдем к сути вопроса и фракталам. Основной бедой современных интерфейсов является их перегруженность и сложность поиска нужных элементов. То есть навигация. С этим пытаются бороться различными способами. Приведу несколько примеров.
1. В меню Старт в Windows выносятся наиболее часто запускаемые программы, а для запуска более редких предлагается заглянуть во вкладку «Все программы».
2. В новом интерфейсе Word 2007 ряд элементов позволяют выполнить как стандартное действие, так и при желании позволяют уточнить команду.
Это означает, что искусственно приходится делить элементы по важности их использования. А количество элементов, которые следует отобразить и спрятать обусловлено размером шрифта и разрешением экрана. Работа с классическим меню, имеющим несколько вложенных уровней еще более ужасна.
Одним из свойств фрактала является, четкое выделение крупных и мелких элементов. И если в «квадратных» интерфейсах мы должны искусственно вводить понятие крупных/мелких, видимых/спрятанных элементов, то во фракталах это может произойти самой собой. При этом каждая часть фрактала подобна и поэтому интерфейс будет единообразным, вне зависимости от глубины погружения, например в пункты меню или настроек.
Я затрудняюсь нарисовать фрактальный интерфейс, тем более красивый. Попробую только схематично отобразить свою мысль. Возьмем интерфейс абстрактного телефона. В нем есть меню верхнего уровня, представленное значками. Нажатие значка открывает подменю и так далее. С фрактальным вариантом, все вроде то же самое, но в нем мы можем быстрее осуществить навигацию, приблизительно зная область в которой находится интересующий нас объект. То есть элемент фрактала, обозначающий глубоко лежащее подменю или конечный элемент, может быть не виден на экране совсем, или обозначаться набором цветных точек. Зная, что мы ищем, мы можем быстро перейти к нужной нам области. Не зная, мы можем двигаться постепенно.
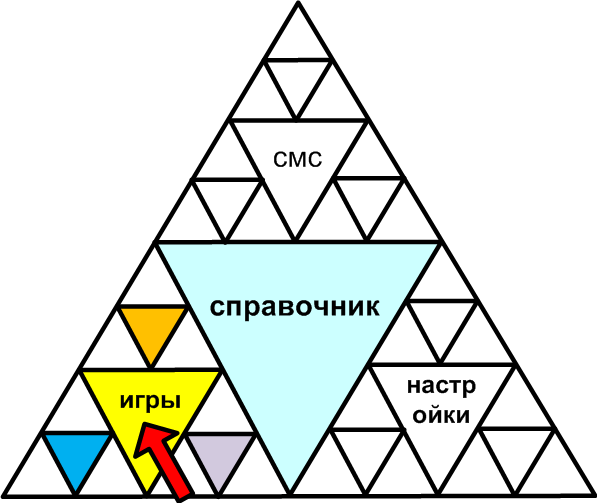
Уверен, что-то подобное уже есть, но явно мало распространено. Крупные объекты подписаны или имеют крупные значки. Более мелкие могут отображаться маленькие значками. Совсем мелкие — просто цветные треугольники. Мы можем двинуться вглубь фрактала постепенно, нажав например раздел «игры». И тогда нам будет показана увеличенная часть фрактала:
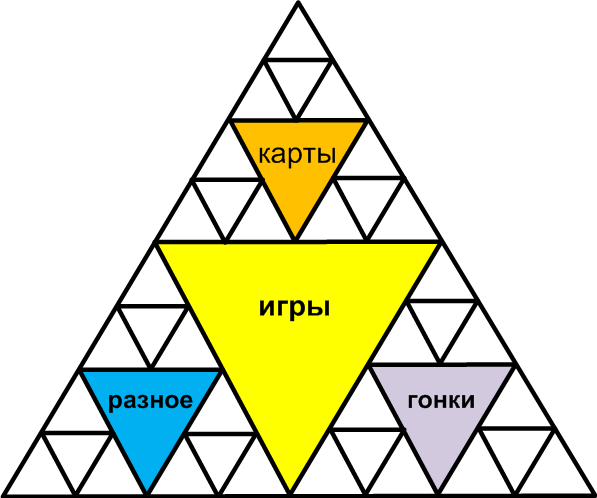
Но что замечательно, мы можем осуществить навигацию гораздо быстрее, если будем помнить, в каком месте находится нужная нам игра. Например, мы сразу можем перейти из главного меню к гонкам, выбрав треугольник нужного цвета.
Так как я это изобразил, это может смотреться не очень удобно, но надеюсь идея ясна. А теперь еще важное преимущество подобного интерфейса выбора. Он легко масштабируется для различных разрешений! Просто чем мельче экран, тем менее детализированным мы будем видеть фрактал.
Надеюсь мои мысли покажутся кому-то интересными и они возьмут их на вооружение. Если для типовых приложений, подобный интерфейс не кажется столь полезным, то например для игр, работающих на различных устройствах, он может оказаться весьма интересным.