Автоматическая оптимизация алгоритмов с помощью быстрого возведения матриц в степень
20 мин
Пусть мы хотим вычислить десятимиллионное число Фибоначчи программой на Python. Функция, использующая тривиальный алгоритм, на моём компьютере будет производить вычисления более 25 минут. Но если применить к функции специальный оптимизирующий декоратор, функция вычислит ответ всего за 18 секунд (в 85 раз быстрее):

Дело в том, что перед выполнением программы интерпретатор Python компилирует все её части в специальный байт-код. Используя метод, описанный хабрапользователем SkidanovAlex, данный декоратор анализирует получившийся байт-код функции и пытается оптимизировать применяющийся там алгоритм. Далее вы увидите, что эта оптимизация может ускорять программу не в определённое количество раз, а асимптотически. Так, чем больше будет количество итераций в цикле, тем в большее количество раз ускорится оптимизированная функция по сравнению с исходной.
Эта статья расскажет о том, в каких случаях и каким образом декоратору удаётся делать подобные оптимизации. Также вы сможете сами скачать и протестировать библиотеку cpmoptimize, содержащую данный декоратор.

Дело в том, что перед выполнением программы интерпретатор Python компилирует все её части в специальный байт-код. Используя метод, описанный хабрапользователем SkidanovAlex, данный декоратор анализирует получившийся байт-код функции и пытается оптимизировать применяющийся там алгоритм. Далее вы увидите, что эта оптимизация может ускорять программу не в определённое количество раз, а асимптотически. Так, чем больше будет количество итераций в цикле, тем в большее количество раз ускорится оптимизированная функция по сравнению с исходной.
Эта статья расскажет о том, в каких случаях и каким образом декоратору удаётся делать подобные оптимизации. Также вы сможете сами скачать и протестировать библиотеку cpmoptimize, содержащую данный декоратор.

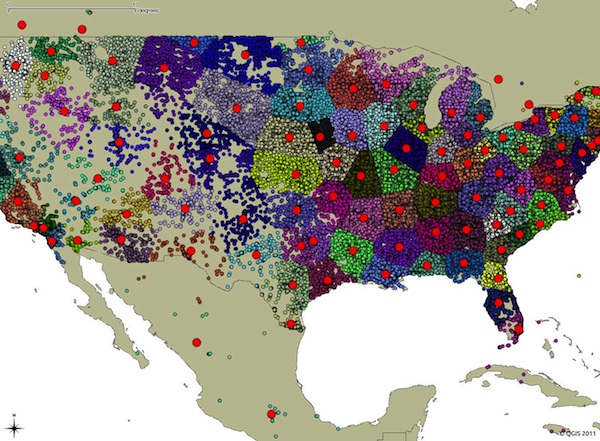
 Частенько читаю Хабр и заметил что в последнее время появились Дайджесты новостей по многим тематикам, таким как веб-разработка на php, разработка на Python, мобильные приложения, но не встретил ни одного подборки по популярному сейчас направлению, а именно анализу данных и big data.
Частенько читаю Хабр и заметил что в последнее время появились Дайджесты новостей по многим тематикам, таким как веб-разработка на php, разработка на Python, мобильные приложения, но не встретил ни одного подборки по популярному сейчас направлению, а именно анализу данных и big data. 


 Как случилось, что искусственный интеллект успешно развивается, а «правильного» определения для него до сих пор нет? Почему не оправдались надежды, возлагавшиеся на нейрокомпьютеры, и в чем заключаются три главные задачи, стоящие перед создателем искусственного интеллекта?
Как случилось, что искусственный интеллект успешно развивается, а «правильного» определения для него до сих пор нет? Почему не оправдались надежды, возлагавшиеся на нейрокомпьютеры, и в чем заключаются три главные задачи, стоящие перед создателем искусственного интеллекта? 
