
Здравствуйте, меня зовут Роман Лапин, я студент 2 курса магистратуры факультета Высшей Школы Общей и Прикладной Физики ННГУ. В этом году мне удалось пройти отбор и поучаствовать в работе Летней Школы Intel в Нижнем Новгороде. Передо мной была поставлена задача определения цвета автомобиля при помощи библиотеки Tensorflow, над которой я работал вместе со своим ментором и инженером команды ICV Алексеем Сидневым.
И вот что у меня получилось.
У подобной задачи есть несколько аспектов:
- Автомобиль может быть раскрашен в несколько цветов, как на КДПВ. А у нас в одном из датасетов, например, была машина с камуфляжной расцветкой.
- В зависимости от освещения и камеры, которая снимает происходящее на дороге, машины одинакового цвета будут выглядеть совсем по-разному. У «засвеченных» автомобилей может быть совсем маленькая часть, отвечающая «истинному» цвету машины.
Определение цвета автомобиля
Цвет автомобиля – это достаточно странная субстанция. У производителя есть чёткое понимание, какого цвета автомобиль они производят, например: фантом, ледниковый, черная жемчужина, плутон, лайм, криптон, ангкор, сердолик, платина, блюз. У ГИБДД мнение о цветах автомобилей достаточно консервативно и сильно ограничено. У каждого отдельного человека восприятие цвета субъективно (можно вспомнить популярную историю про цвет платья). Таким образом, нами было принято решение выполнить разметку следующим образом.
На каждом изображении были отмечены координаты вершин окаймляющих прямоугольников вокруг автомобилей (далее я буду использовать английский вариант — car bounding box) и внутри них – области, которые лучше всего характеризуют цвет транспортных средств (color box). Число последних равно цветности машины (n х color box – n-цветный автомобиль).
Здесь и далее номера автомобилей замазаны для возможности опубликовать фотографии в открытом доступе.

Разметка автомобилей датасета
В дальнейшем мы работали с двумя цветовыми пространствами – RGB и LAB – с соответственно 8 и 810/81 классами. Для сравнения результатов разных подходов мы использовали для определения цвета 8 классов в RGB, которые получаются разбиением BGR куба на 8 равных малых кубиков. Их можно легко назвать общепринятыми названиями: белый, черный, красный, зеленый, голубой, розовый, желтый, циан. Для оценки ошибки какого-либо метода мы уже использовали цветовое пространство LAB, в котором определено расстояние между цветами.
Есть два интуитивных способа определения цвета по color box: средний или медианный цвет. Но в color box встречаются пиксели самых разных цветов, поэтому хотелось узнать, насколько точно работает каждый из этих двух подходов.
Для 8 цветов RGB для каждого color box каждой машины в датасете мы определили средний цвет пикселей и медианный, результаты приведены на рисунках ниже. В строках отмечены «истинные» цвета – т. е. цвета, определенные соответственно как средний или как медиана, в столбцах – цвета, встречающиеся в принципе. При добавлении одной машины в таблицу число пикселей каждого цвета нормировалось на их количество, т. е. сумма всех значений, добавляемых в строку, равнялась единице.
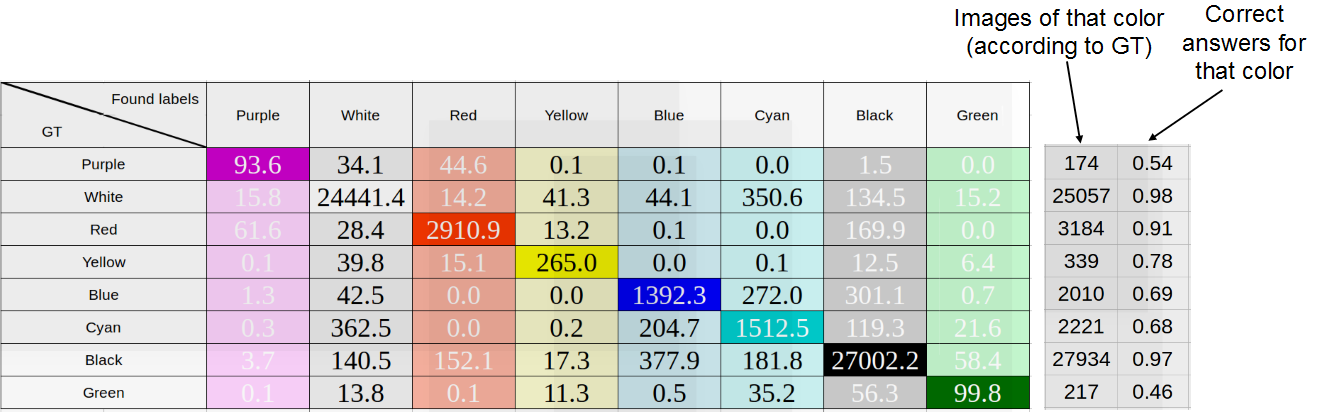
Исследование точности определения цвета машины как среднего цвета пикселей color ’abox. Средняя точность: 75%
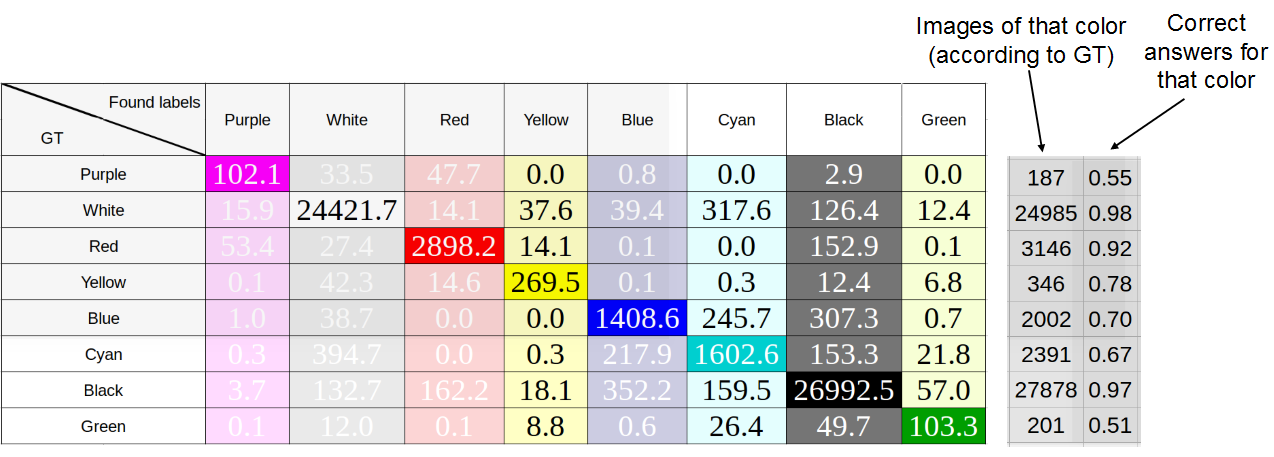
Исследование точности определения цвета машины как медианного цвета пикселей color box. Средняя точность: 76%
Как видим, особой разницы между методами нет, что свидетельствует о хорошей разметке. В дальнейшем мы использовали медиану, т. к. она показала лучший результат.
Определение цвета автомобиля будет происходить на основании области внутри car bounding box.
Нужны ли сети?
Неизбежен вопрос: а так ли нужны нейронные сети для решения интуитивно простой задачи? Может, можно таким же образом взять медианный или средний цвет пикселей car bounding box? На рисунках ниже приведен результат такого подхода. Как будет показано позднее, он хуже, чем метод с использованием нейронных сетей.
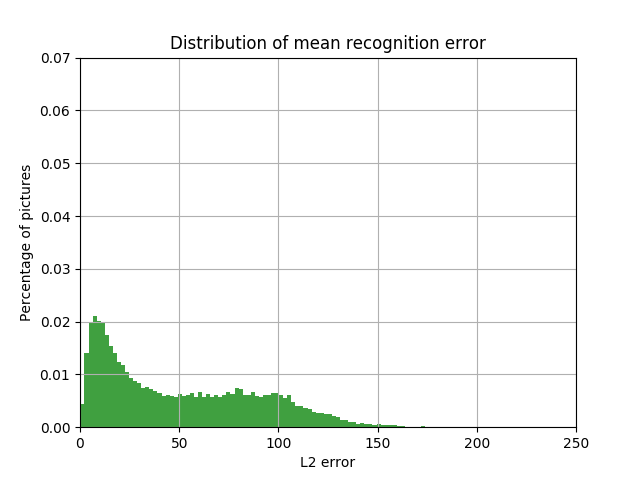
Распределение доли автомобилей с величиной L2 ошибки в пространстве LAB между цветом color box, определённым как среднее, и цветом car bounding box’a от величины этой ошибки
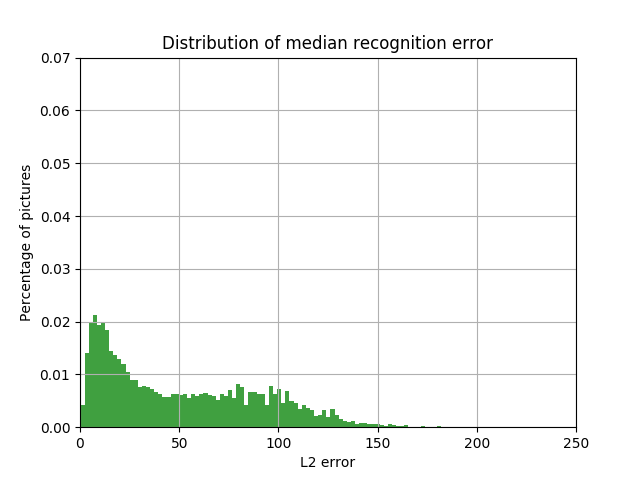
Распределение доли автомобилей с величиной L2 ошибки в пространстве LAB между цветом color box, определённым как медиана, и цветом car bounding box от величины этой ошибки
Описание подхода к задаче
В нашей работе мы использовали архитектуру Resnet-10 для выделения признаков. Для решения one label и multilabel задач были выбраны активационные функции софтмакс и сигмоида соответственно.
Важным вопросом был выбор метрики, по которой мы могли бы сравнить наши результаты. В случае one label задачи можно выбрать класс, соответствующий максимальному отклику. Однако подобное решение, очевидно, не будет работать в случае multilabel/многоцветных машин, поскольку argmax выдаёт один, наиболее вероятный, цвет. Метрика L1 зависит от числа классов, поэтому тоже не могла быть использована для сравнения всех результатов. Поэтому было решено остановиться на метрике площади под ROC кривой (ROC AUC – area under curve) как универсальной и общепризнанной.
Мы работали в двух цветовых простанствах. Первое – стандартное RGB, в котором мы выбрали 8 классов: разбили RGB-кубик на 8 одинаковых подкубиков: белый, черный, красный, зеленый, голубой, розовый, желтый, циан. Такое разбиение очень грубое, но простое.
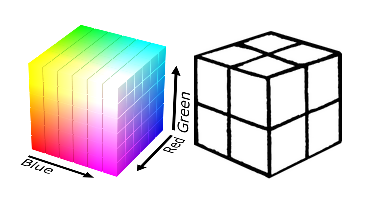
Разбитие цветового пространства RGB на 8 областей
Кроме того, мы проводили исследования с цветовым пространством LAB, в которм использовали разбиение на 810 классов. Почему столько? LAB был введен после того, как американский учёный Дэвид МакАдам установил, что существуют области цветов, которые не различимы человеческим глазом (эллипсы МакАдама). LAB был построен так, чтобы в нём эти эллипсы имели вид окружностей (в сечении постоянного L – яркости).
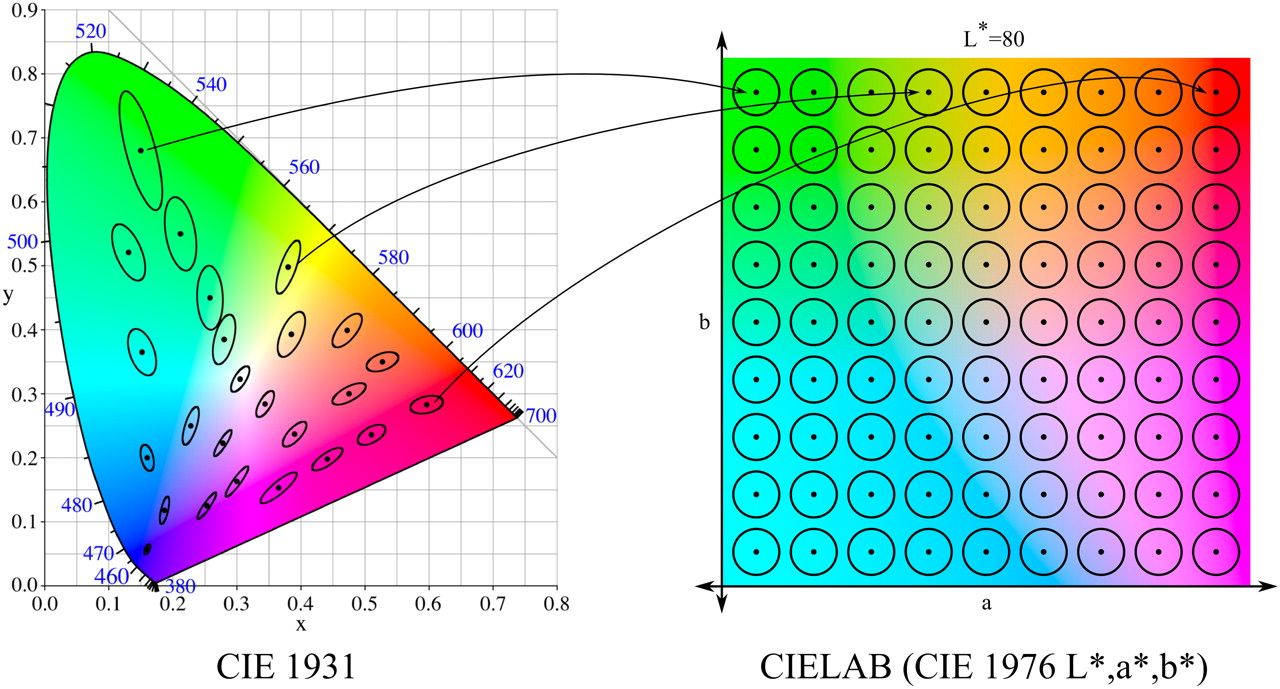
Эллипсы МакАдама и цветовое пространство LAB (источник картинки)
Всего в сечении таких окружностей ��� 81. Мы брали шаг 10 по параметру L (от 0 до 100), получив 810 классов. Кроме того, мы провели эксперимент с постоянным L и, соответственно, 81 классом.
RGB и LAB
Для 8-классовой задачи и пространства RGB получились следующие результаты:
| Activation function | Multilabel task | ROC AUC |
|---|---|---|
| softmax | ― | 0.97 |
| sigmoid | ✓ | 0.88 |
Кажется, что результат для multilabel задачи уже достаточно хороший. Для проверки этого предположения мы построили матрицу ошибок, взяв в качестве порогового значения для вероятности 0.55. Т.е. при превышении этого значения в вероятности для соответствующего цвета мы считаем, что машина покрашена и в этот цвет. Несмотря на то, что порог выбран достаточно низким, при нём можно увидеть характерные ошибки в определении расцветки автомобиля и сделать выводы.
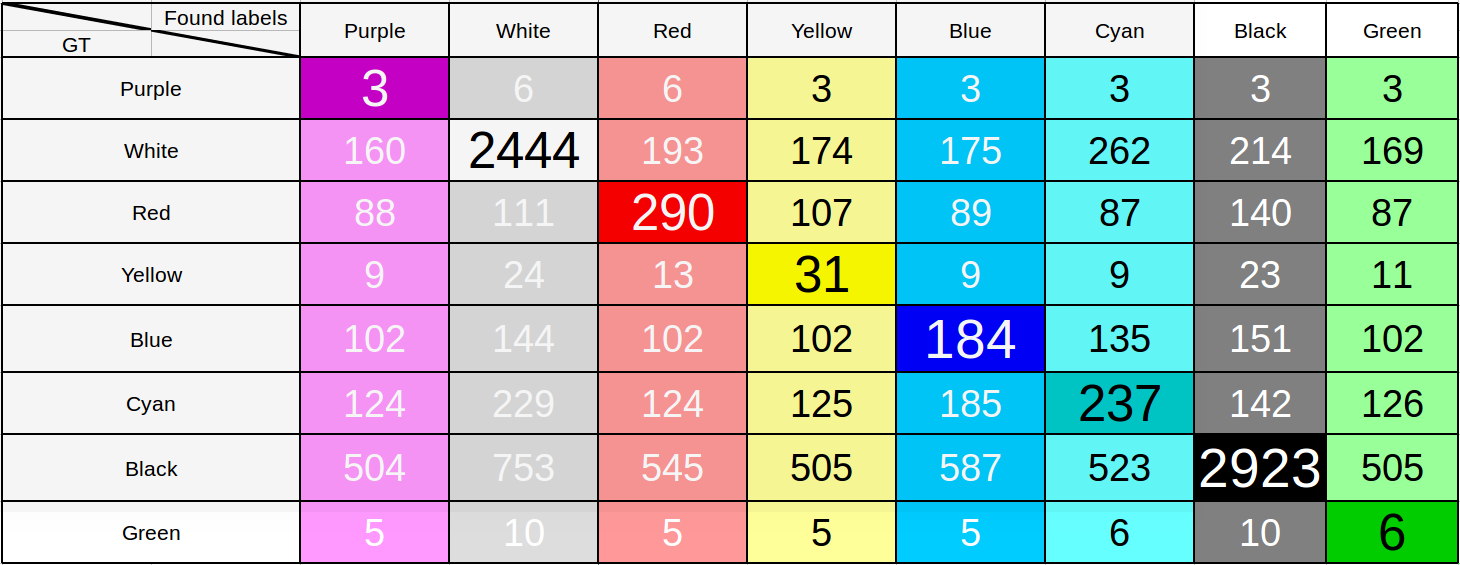
Таблица результатов распознавания цвета машин в 8 классовой задаче
Достаточно посмотреть на строчки, соответствующую зелёному или розовому цветам, чтобы убедиться, что модель далеко не идеальна. К вопросу о том, почему при большой величине по метрике получается такой странный неудачный результат, мы ещё вернёмся, сейчас же сразу обозначим: при рассмотрении всего лишь 8 классов огромное число цветов попадает в классы «белый» и «черный», поэтому и такой результат.
Поэтому далее перейдём в цветовое пространство LAB и проведем исследования там.
| Activation func | Multilabel task | ROC AUC |
|---|---|---|
| softmax | ― | 0.915 |
| sigmoid | ✓ | 0.846 |
Результат получился меньше, что логично, так как число классов увеличилось на два порядка. Взяв результат по сигмоиде за отправную точку, мы попробовали улучшить нашу модель.
LAB: эксперименты с разными весами
До этого все эксперименты производились с единичными весами в функции потерь (loss):
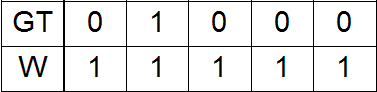
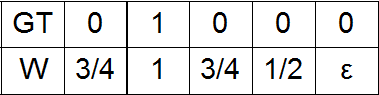
Здесь GT – ground truth, W – weights.
В цветовом пространстве LAB можно ввести расстояние. Допустим, у нас в GT есть одна единица. Тогда она соответствует какому-то прямоугольному параллелепипеду в цветовом пространстве LAB. Этот параллелепипед (точнее, его центр) удален на разное расстояние от всех остальных параллелепипедов (опять же, их центров). В зависимости от этого расстояния можно проэкспериментировать со следующими вариантами весов:
a) Ноль на месте единицы в GT, а при удалении от него – возрастание весов;
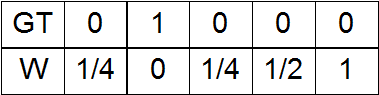
b) Наоборот, на месте единицы в GT – единица, при удалении – спадание весов;
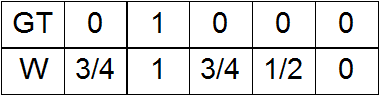
c) Вариант a) плюс небольшая гауссова добавка с амплитудой ½ на месте единицы в GT;
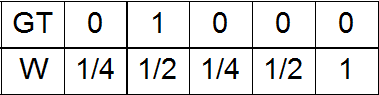
d) Вариант a) плюс небольшая гауссова добавка с амплитудой 1 на месте единицы в GT;
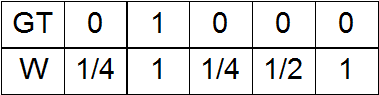
e) Вариант b) c малой добавкой при максимальном удалении от единицы в GT.
Последний вариант весов, с которым мы провели эксперименты, ― как мы его назвали, тройной гаусс, а именно три нормальных распределения с центрами на месте единиц в GT, а также при наибольшем удалении от них.
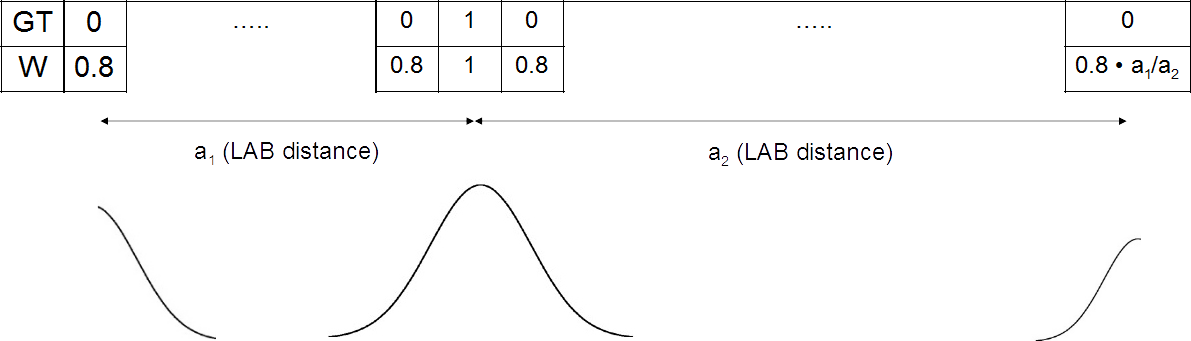
Три нормальных распределения с центрами на месте единиц в GT и при наибольшем удалении от них
Его придется объяснить чуть подробнее. Можно выбрать два наиболее удаленных параллелепипеда, а, значит, класса, и сравнить их по удаленности от исходного. Для класса, соответствующего дальнему, амплитуда распределения задана равной 0.8, а для второго – в m раз меньше, где m есть отношение расстояния от исходного до дальнего удаленного к дистанции между исходным и ближним.
Получившиеся результаты приведены в таблице. Из-за того, что в весах варианта а) встречались нулевые веса – как раз у единиц в GT, результат по ним вышел даже хуже отправной точки, т. к. сеть не учитывала удачные определения цвета, обучаясь хуже. Варианты весов b) и e) практически совпадали, поэтому совпал и результат по ним. Наибольший прирост по процентным пунктам по сравнению с отправным результатом показал вариант весов f) – тройной гаусс.
| Activation function | Number of classes | Weights type | ROC AUC |
|---|---|---|---|
| sigmoid | 810 | a) | 0.844 |
| b), e) | 0.848 | ||
| c) | 0.888 | ||
| d) | 0.879 | ||
| f) | 0.909 |
LAВ: эксперименты с новыми лейблами
Итак, мы провели эксперименты с разными весами в loss. Затем решили попробовать оставить веса единичными, а изменить лейблы, которые передаются в функцию потерь и используются для оптимизации сети. Если до этого лейблы совпадали с GT, то теперь решили использовать опять же гауссовы распределения с центрами на месте единиц в GT:
Мотивация у такого решения следующая. Дело в том, что при обычных лейблах все машины в датасетах попадают в фиксированное число классов, меньшее 810, поэтому сеть учится определять цвет автомобилей только этих классов. При новых лейблах уже во все классы попадают ненулевые значения и можно ожидать увеличение точности определения цвета автомобиля. Мы проэкспериментировали с двумя сигмами (среднеквадратичными отклонениями) для вышеописанных гауссовых распределений: 41.9 и 20.9. Почему такими? Первая сигма выбрана так: взято минимальное расстояние между классами (28) и сигма определяется из условия спадания распределения в два раза в соседнем к GT’ному классу. А вторая сигма просто меньше первой в два разa.
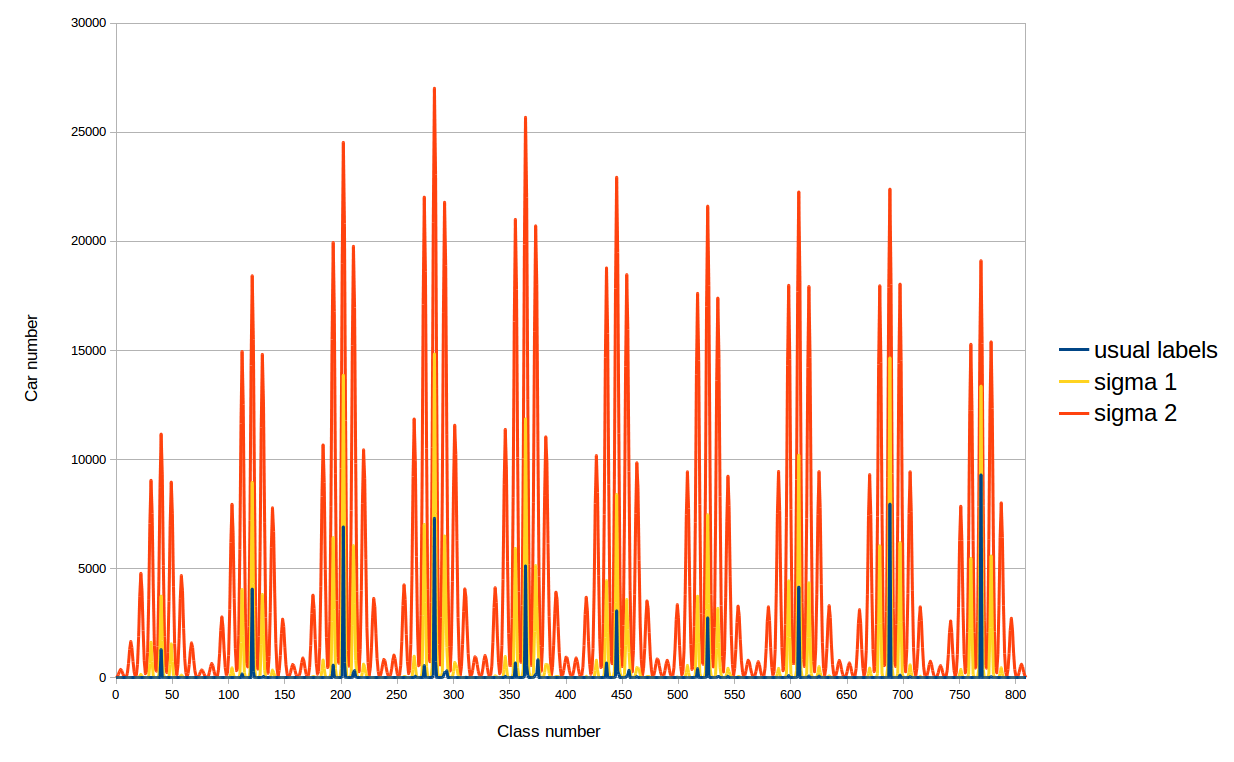
Распределение автомобилей тренировочного датасета по классам при разных лейблах в loss
И действительно, удалось ещё больше улучшить результат с помощью такого трюка, как и показано в таблице. В итоге точность определения достигла 0.955!
| Activation function | Number of classes | Labels type | Weights type | ROC AUC |
|---|---|---|---|---|
| sigmoid | 810 | usual | ones | 0.846 |
| usual | three gauss | 0.909 | ||
| new, σ1 | three gauss | 0.955 | ||
| new, σ2 | 0.946 |
LAB:81
Если же рассказывать про неудачные эксперименты, то необходимо упомянуть про попытку натренировать сеть с 81 классами и постоянным параметром L. Нами было замечено в ходе предыдущих экспериментов, что как раз яркость определяется сетью довольно точно, и мы решили потренировать только параметры a и b (так называются две другие координаты в LAB). К сожалению, несмотря на то, что сеть смогла прекрасно натренироваться в плоскости, показав большее значение по метрике, идея задавать параметр L на выходе сети как средний по car bounding box потерпела крах и настоящий цвет и определённый таким образом отличались очень сильно.
Сравнение с решением задачи без использования нейронных сетей
А теперь давайте вернёмся к самому началу и сравним то, что получилось у нас, с распознаванием цве��а автомобиля без использования нейронных сетей.
Результаты приведены на рисунках ниже. Видно, что и пик стал больше в 3 раза, и количество машин с большой ошибкой между истинным и определённым цветом существенно снизилось.

Распределение доли автомобилей с величиной L2 ошибки в пространстве LAB между цветом color bounding box, определённым как медиана, и цветом car bounding box от величины этой ошибки
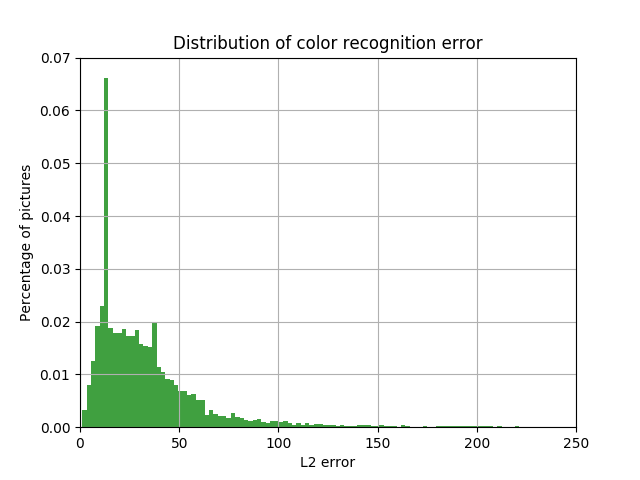
Распределение доли автомобилей с величиной L2 ошибки в пространстве LAB между цветом на выходе нейронной сети, и цветом car bounding box от величины этой ошибки
Примеры
Далее приведу примеры распознавания цвета автомобилей. Первый – чёрная машина (типичный случай) распознана как чёрная, причём расстояние в пространстве LAB между истинным цветом и определённым (18.16) меньше минимального расстояния между классами (28). На втором рисунке сеть смогла не только определить, что авто засвечено (имеется большая вероятность, отвечающая одному из классов белых цветов), но и его настоящий цвет (серебристый). Однако машина со следующего рисунка, также засвеченная, не была детектирована сетью как красная. Цвет автомобиля, изображённого на рисунке далее, сеть определить не смогла совсем, что следует из того, что вероятности для всех цветов слишком малы.
Во многом задача была обусловлена необходимостью распознавать многоцветные машины. На последнем рисунке изображена двухцветная чёрно-жёлтая машина. Чёрный цвет сеть распознала с наибольшей вероятностью, что, видимо, связано с преобладанием машин такого и похожих цветов в тренировочном датасете, а жёлтый цвет, близкий к истинному, вошёл в топ-3.
 |
 |
|---|
 |
 |
|---|
 |
 |
|---|
 |
 |
|---|
 |
 |
|---|
ROC curve: визуализация и проблемы
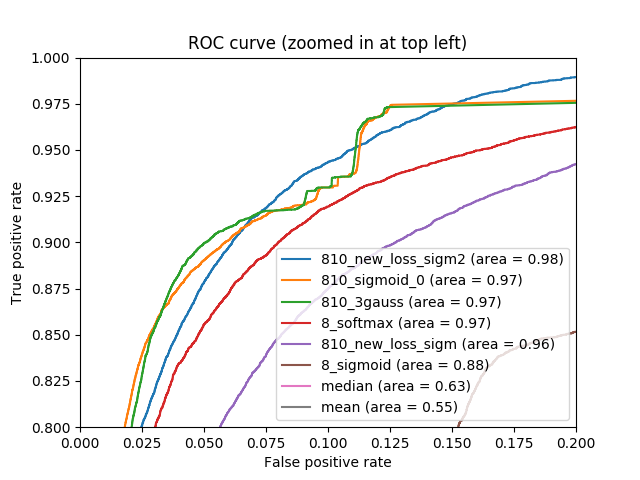
Итак, на выходе мы получили достаточно высокий результат по метрике. На следующем рисунке приведены ROC кривые как для решения задачи с 8 классами, так и для задачи с 810 классами, а также решения без использования нейронных сетей. Видно, что результат получается немного другой, чем тот, что был выписан ранее. Приведенные ранее результаты были получены с использованием TensorFlow, графики ниже были получены с использованием пакета scikit-learn.
 |
 |
|---|
Можно брать в качестве пороговых значений какие-либо фиксированные числа (например, Tensorflow при задании соответствующего параметра равным 50 берёт столько же порогов от 0 до 1 через равные промежутки), можно – значения на выходе сети, а можно ограничивать их снизу, чтобы не рассматривать значения порядка 10-4, например. Результат последнего подхода приведен на следующем рисунке.
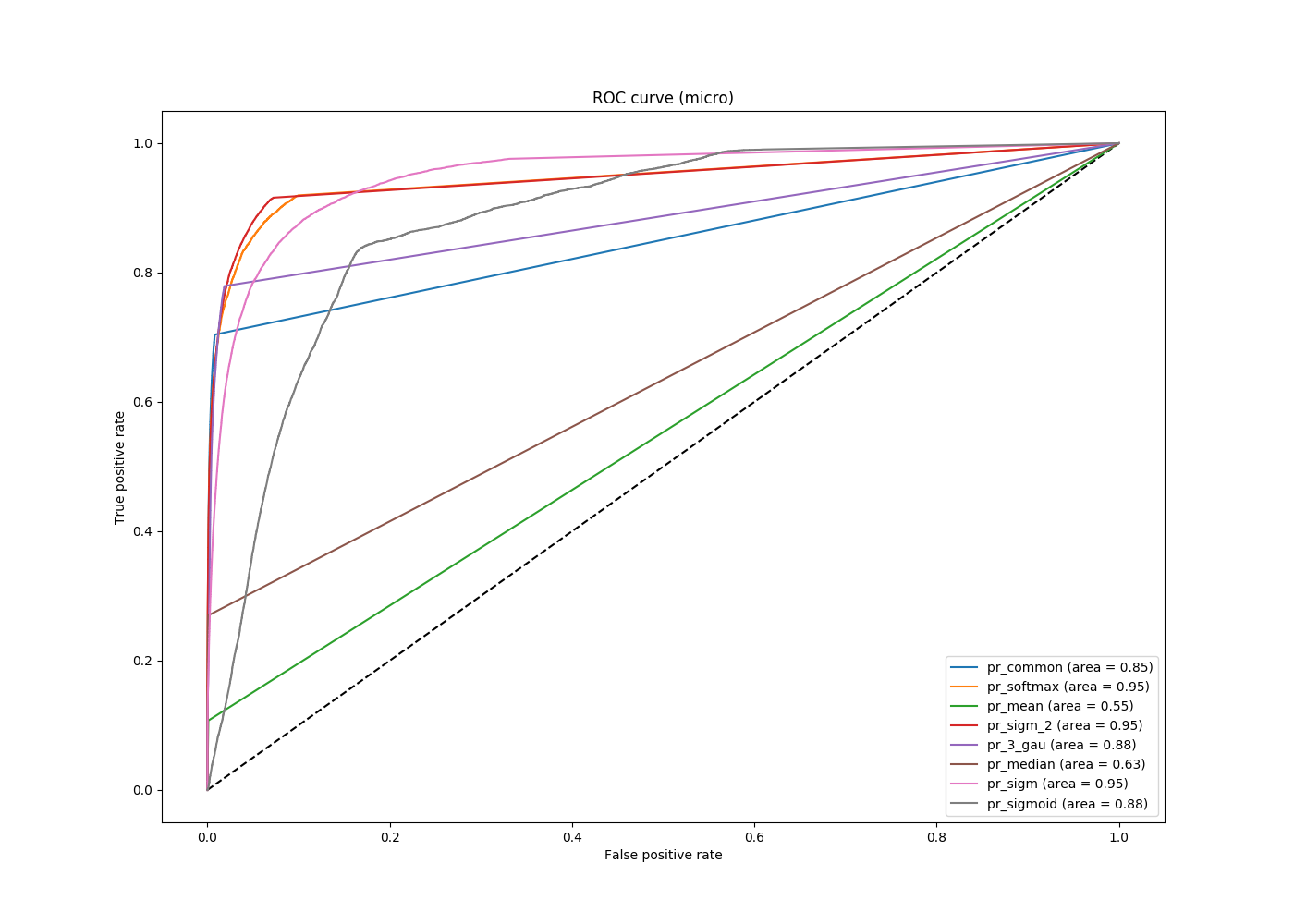
ROC кривая для нескольких вариантов решения задачи c порогом 10-4
Видно, что все кривые, отвечающие решению задачи с использованием нейронных сетей, характерно лучше (находятся выше) решению задачи без них, но между первыми нельзя выбрать одну однозначно лучшую кривую. В зависимости от того, какой порог выберет пользователь, разные кривые будут отвечать разным оптимальным решениям задачи. Поэтому, с одной стороны, мы нашли такой подход, который позволяет достаточно точно определить цвет машины и показывает высокую метрику, с другой – показали, что предел пока не достигнут и метрика площади под ROC кривой имеет свои недостатки.
Готов ответить на вопросы и выслушать замечания в комментариях.
