Комментарии 25
<Как мог бы выглядеть вывод формулы для дискриминанта в XVII веке>.
А как выводится эта формула не окольными путями?
Я сейчас правда на хабре?
Мне кажется, или вы вывели формулу через ее саму же… странное чувство.
Чтобы эта формула стала интегралом, ей не хватает неизвестной константы.
Также нельзя оставлять без внимания тот факт, что формула для РУД выше по факту есть результат взятия интеграла от формулы скорости такого движения.
Чтобы эта формула стала интегралом, ей не хватает неизвестной константы.
Неизвестная константа — это 
, и в данном случае она равна нулю (т.к. это перемещение по оси OX). P.S. Можно взять интеграл от формулы скорости при ПРУД. Или из графика 
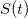найти площадь фигуры. Там вылезет трапеция.
Или вообще можно так.
Этим мы показываем, что формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Спасибо за внимание!
, и в данном случае она равна нулю (т.к. это перемещение по оси OX). P.S. Можно взять интеграл от формулы скорости при ПРУД. Или из графика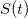 
найти площадь фигуры. Там вылезет трапеция.Или вообще можно так.
Этим мы показываем, что формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Спасибо за внимание!
Всегда было интересно зачем в школе пичкают этими уравнениями. За 30 лет жизни они мне ниразу не пригодились, даже косвенно.
Может кто знает где применяются квадратные уровнения?
Может кто знает где применяются квадратные уровнения?
«Математику только затем учить надо, что она ум в порядок приводит» (М. В. Ломоносов).
А вот «пичкать» действительно не надо.
А вот «пичкать» действительно не надо.
Ваш вопрос равен вопросу :«Нужна ли математика? „
Там где есть квадратичные зависимости, очевидно. Например — в школьной физике их хватает. Или физика тоже не нужна?
А ещё квадратные уравнения подготавливают к знакомству с полиномами более высоких порядков. Которые используются да хоть в той же интерполяции сплайнами.
А косвенно вы решаете эту задачу каждый раз, когда прикидываете, успеет ли затормозить машина перед вами.
А ещё квадратные уравнения подготавливают к знакомству с полиномами более высоких порядков. Которые используются да хоть в той же интерполяции сплайнами.
А косвенно вы решаете эту задачу каждый раз, когда прикидываете, успеет ли затормозить машина перед вами.
Они негде не применяются сами по себе. Они возникают при построении математических моделей, коих решить вам предстоит для получения результата. И чтобы постоянно не перевыводить все, люди фиксируют формулы/алгоритмы решения. Все ради скорости. Время — самый ценный ресурс.
Например, нужно решить квадратное уравнение, чтобы найти пересечение окружности с отрезком. Будете писать 2D-игру с физикой — без квадратных уравнений не обойдётесь.
Например, при построении решений некоторых обыкновенных линейных дифференциальных уравнений (решение характеристического уравнения), а такие уравнения часто возникают в инженерных приложениях.
У Я.И. Перельмана в его книге «Занимательная алгебра» есть задача о громкоговорителях (стр. 140-141), решение которой сводится к квадратному уравнению:
На площади установлено 13 громкоговорителей, разбитых на две группы: в одной 4, в другой 9 аппаратов (от себя: то есть громкоговорители висят на двух столбах). Расстояние между группами 50 м. Где надо стать, чтобы звуки обеих групп доносились с одинаковой силой?
На площади установлено 13 громкоговорителей, разбитых на две группы: в одной 4, в другой 9 аппаратов (от себя: то есть громкоговорители висят на двух столбах). Расстояние между группами 50 м. Где надо стать, чтобы звуки обеих групп доносились с одинаковой силой?
а какие ещё есть аналогичные книги?
Глянул книгу Г.М. Розенблата «Сухое трение и односторонние связи», стр. 99-108 — «О безотрывных движениях волчка на гладкой плоскости» (волчок Томсона). Там сформулирован критерий, основанный на решении квадратного уравнения и позволяющий понять, оторвётся ли сферический волчок (со смещенным центром тяжести) от горизонтальной плоскости при заданных параметрах движения.
Можно ещё посмотреть мой топик о неполном кубическом уравнении. Если взять для силы сопротивления воздуха закон Стокса, то получится квадратное уравнение.
Можно ещё посмотреть мой топик о неполном кубическом уравнении. Если взять для силы сопротивления воздуха закон Стокса, то получится квадратное уравнение.
Ещё пример — задача на экстремум. Требуется при заданных издержках (суммарные затраты производства b = c1 * x1 + c2 * x2) определить количества x1 и x2 факторов производства (то есть затраты определенных продуктов в количествах x1 >= 0 и x2 >= 0, с1 и c2 — их цены за единицу), которые максимизируют объём продукции f(x1, x2). Можно задать такой вид функции f, что решение данной экономической задачи сведётся к квадратному уравнению.
Дифференцируй, Люк. Теперь ждем статью про SGD.
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
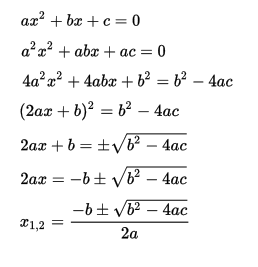
Решение квадратных уравнений через производные