
Если рассматривать сегодняшние алгоритмы машинного обучения с движением от невежества (низ) к осознанию (верх) то текущие алгоритмы похожи на прыжок. После прыжка происходит замедление скорости развития (обучающая способность) и неминуемый разворот и падение (переобучение). Все усилия сводятся к попыткам приложить как можно больше сил к прыжку, что увеличивает высоту прыжка но кардинально не меняет результатов. Прокачивая прыжки мы увеличиваем высоту, но не учимся летать. Для освоения техники «контролируемого полета» потребуется переосмыслить некоторые базовые принципы.
В нейронных сетях используется статическая структура которая не позволяет выйти за рамки установленной обучающей способности всей конструкции. Зафиксировав размеры сети из фиксированного количества нейронов мы ограничиваем размер обучающей способности сети которую сеть никогда не сможет обойти. Установка за ведома большего количества нейронов при создании сети позволяет увеличить обучающу�� способность, но замедлит время обучения. Динамическое изменение структуры сети во время обучения и использование двоичных данных наделит сеть уникальными свойствами и позволит обойти указанные ограничения.
1. Динамическая структура сети
Сеть самостоятельно должна принимать решения о своих размерах. По мере необходимости расти в нужном направлении увеличивая свои размеры. Один нейрон, слой или два при создании сети мы не можем однозначно знать необходимой обучающей способности сети а следовательно и ее размеры. Наша сеть должна начинаться с нуля (полного отсутствия структуры) и должна получить возможность расширяться в нужную сторону самостоятельно при поступления новых обучающих данных.
2. Затухание сигнала
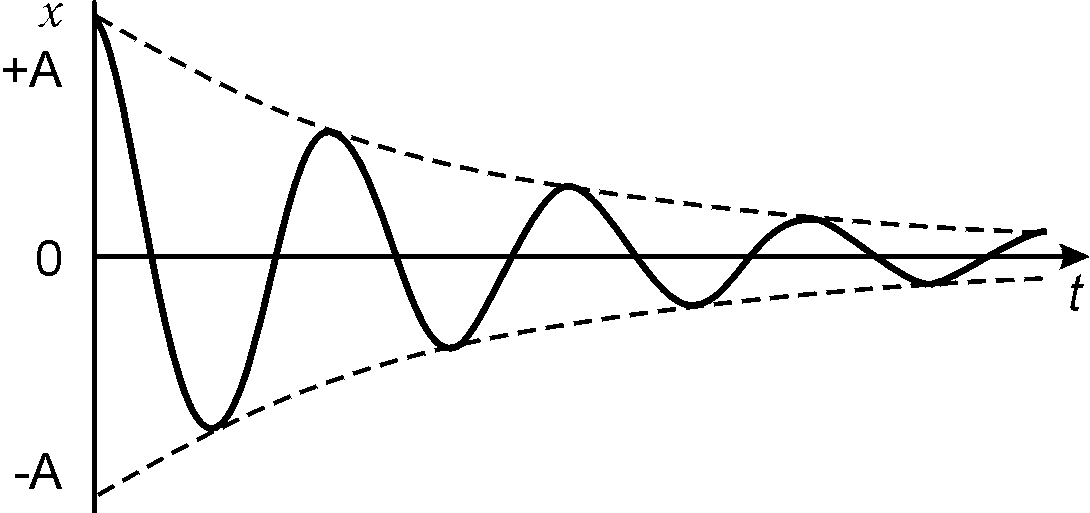
Нейронные сети занимаясь суммированием сигнала используют «аналоговый» подход к расчету. Многократные преобразования приводят к затуханию сигнала и его потере при передаче. На больших размерах сети «аналоговые» методы расчета будет неминуемо приводить к потерям. В нейронных сетях проблему затухания сигнала могут решать рекуррентные сети, по сути являясь костылем лишь уменьшая проблему, не решая ее полностью. Решением будем использование двоичного сигнала. Количество преобразований такого сигнала не приводит к его затуханию и потере при преобразованиях.
3. Обучающая способность сети

Расширяя структуру по мере обучения мы увеличиваем и ее обучающую способность. Сеть сама определяет исходя из задачи в каком направлении развиваться и какое количество нейронов необходимо для решения поставленной задачи. Размер сети ограничивает только вычислительная способность серверов и ограничения размеров жесткого диска.
4. Обучение сети
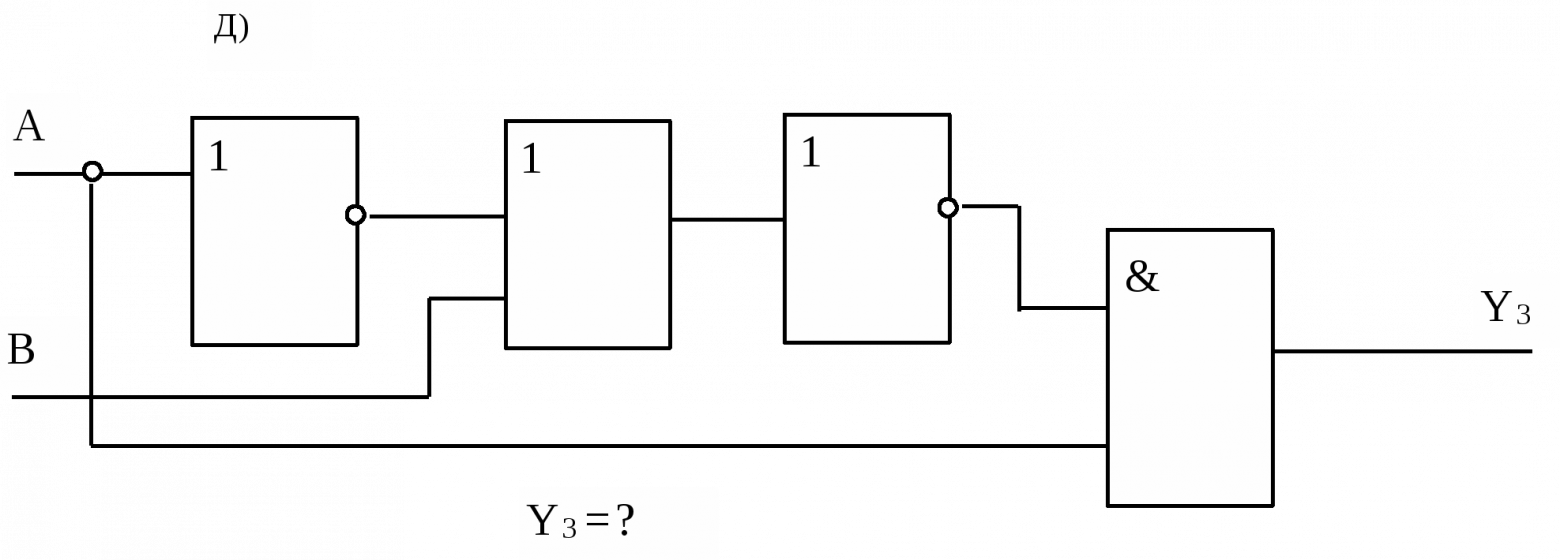
При изменении сигналов с аналоговых на двоичные сети получает возможность ускоренного обучения. Обучение дает однозначную установку сигнала на выходе. Сам процесс обучения изменяет лишь малую часть нейронов, оставляя значительную их часть без изменений. Время на обучение сокращается многократно ограничиваясь изменениям нескольких элементов сети.
5. Расчет сети
Для расчета нейронной сети нам необходимо расчитать все элементы. Пропуск расчета даже части нейронов может привести к эффекту бабочки где малозначительный сигнал может поменять результат всего расчета. Природа двоичных сигналов другая. На каждом из этапов можно без последствий исключить часть данных из расчета. Чем больше такая сеть, тем большее количество элементов мы можем игнорировать в расчетах. Расчеты результатов сетей сводится к расчету небольшого количества элементов вплоть до долей процента от сети. Для расчета достаточно 3.2% (32 нейрона) при сети в тысячу нейронов, 0.1% (1 тыс) при миллионе «нейронов» в сети и 0.003% (32 тыс) при сети размером в миллиард «нейронов». С увеличением размеров сети процент обязательных для расчета нейронов уменьшается.
6. Интерпретац��я результатов
В нейронных сетях веса помноженные на коэффициенты не дают возможности установить источник сигнала. Все входящие сигналы нейронной сети без исключения оказывают влияние на результат, усложняя понимание причин приведших к его формированию. Влияние двоичных сигналов на результат может быть нулевым, частичным или полным, что однозначно говорит об участии исходных данных в расчете. Двоичные методы расчета сигналов позволяют отследить связь входящих данных с результатом и определить степень влияния исходных данных на формирование результата.
Все вышесказанное говорит о необходимости изменения подходов к алгоритмам машинного обучения. Классические методы не дают полного контроля сети и однозначного понимания происходящих в ней процессов. Для достижения «контролируемого полета» требуется обеспечить надежность преобразования сигналов внутри сети и динамическое формирования структуры «на лету».
