В 67 году н.э. во время иудейско-римской войны Иосиф Флавий и сорок мятежников оказались в ловушке в пещере. Предпочтя самоубийство плену, они решили встать в круг и убивать каждого третьего из оставшихся в живых. Иосиф Флавий хотел остаться в живых и понял, где он должен стоять в кругу, чтобы остаться в живых в череде казней. Так он выжил, чтобы рассказать эту легенду.
На следующем собеседовании по алгоритмам вам может попасться алгоритмическая задача, основанная на этой легенде. По кругу стоят мятежников, пронумерованных от
до
. Начиная с нулевого, они убивают по кругу каждого
-го оставшегося в живых. Обозначим через
номер мятежника, оставшегося последним. Напишите программу, которая по данным
и
находит
. Пример ниже показывает, что
.
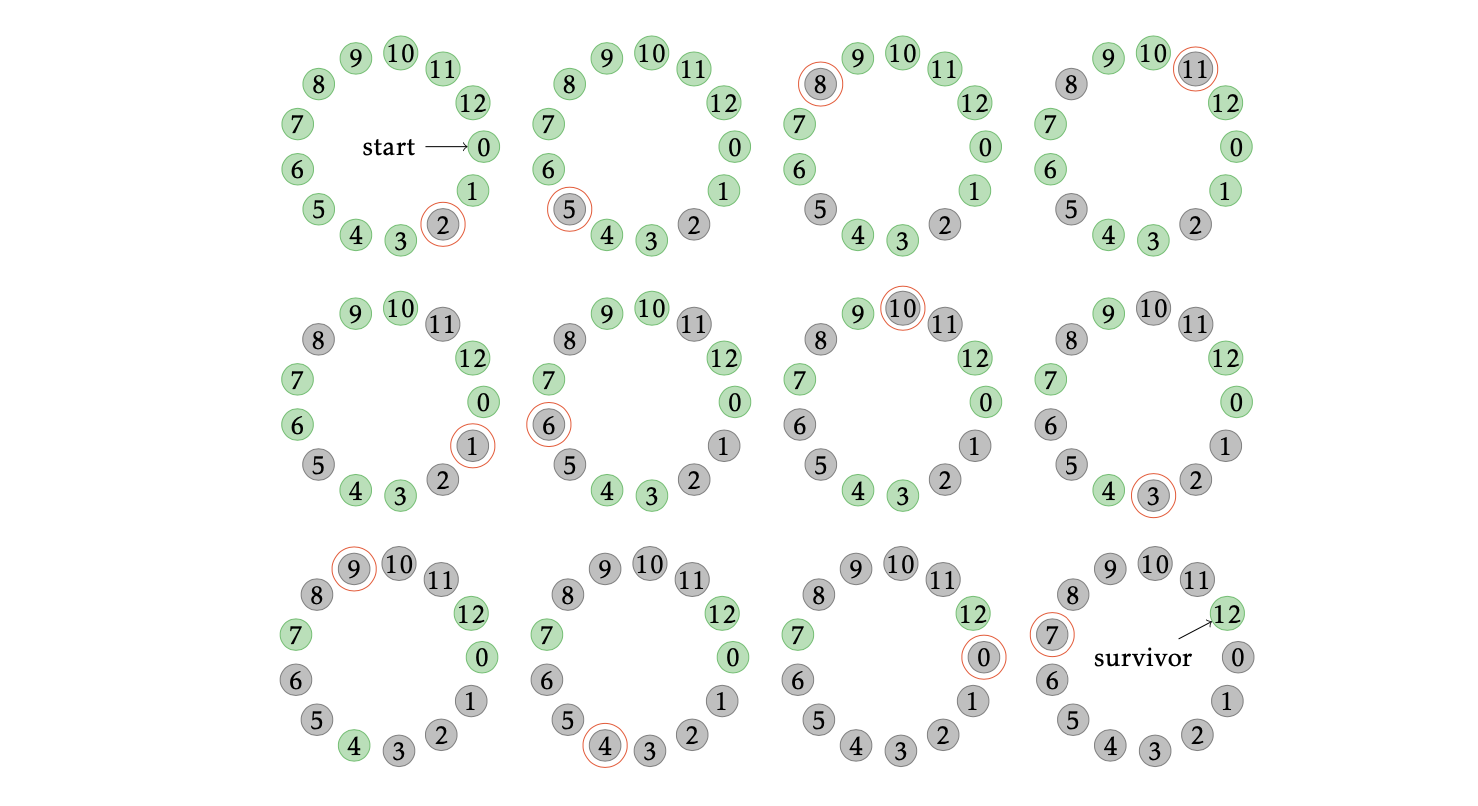
Ниже мы рассмотрим несколько алгоритмов для решения этой задачи. Читать вам будет гораздо интереснее, если вы перед прочтением придумаете алгоритм для этой задачи самостоятельно: во-первых, полезно потренироваться решать задачи с собеседований; во-вторых, решение гораздо лучше запоминается, если придумать его самостоятельно; в-третьих, удовольствие и уверенность, полученные от самостоятельного решения, мало с чем сравнятся =) Ниже мы приводим наглядную визуализацию и подробные описания алгоритмов.
Наивный алгоритм
Наивный способ решения задачи — промоделировать: завести массив размера , в котором отмечать, кто из мятежников всё ещё жив, и, проходя массив слева направо, отмечать каждого
-го (из всё ещё живых) как убитого. Код на Python:
def josephus(n, k): alive = [True] * n num_survivors, current_position, index = n, 0, 0 while num_survivors: if alive[current_position]: index += 1 if index == k: num_survivors = num_survivors - 1 if not num_survivors: return current_position else: alive[current_position] = False index = 0 current_position = (current_position + 1) % n
Время работы работы этого алгоритма — : после каждого прохода по массиву количество живых мятежников уменьшается примерно в
раз, поэтому понадобится примерно
проходов. Ниже мы построим более простой и быстрый алгоритм.
Быстрый алгоритм
После того, как первый мятежник убит, остаётся та же самая задача: по-прежнему убивают каждого -го, но всего мятежников теперь
, у них другие номера и убийства начинаются уже не с нулевого, а с мятежника с номером
.
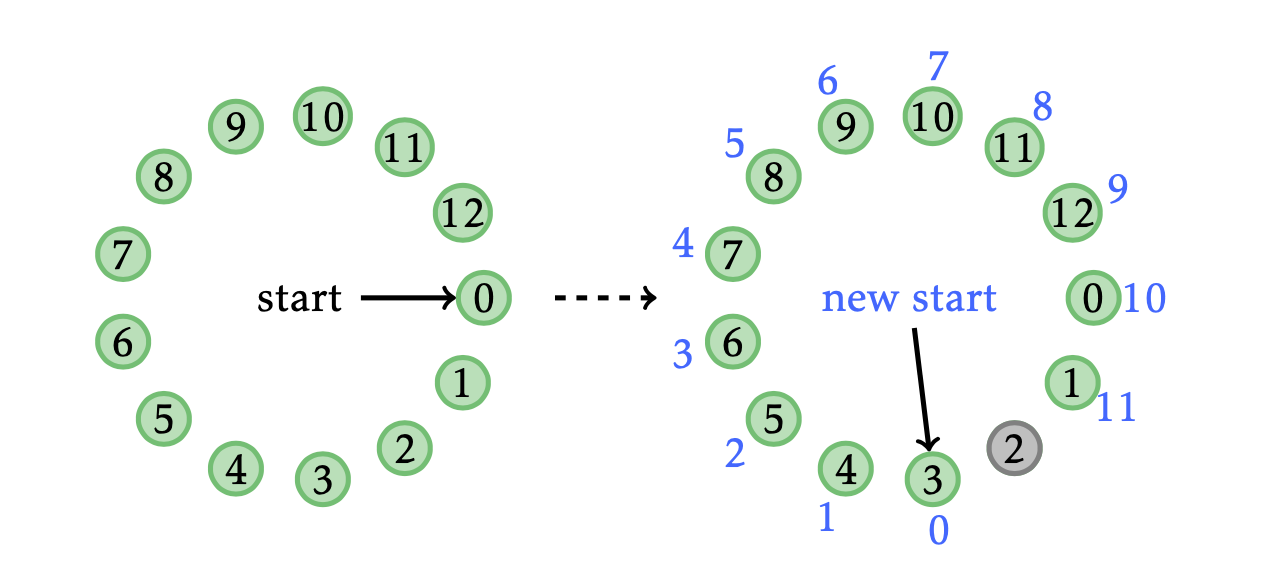
Новые и старые номера мятежников связаны такой формулой:
Это приводит к такому рекуррентному соотношению:
В свою очередь, это рекуррентное соотношение легко переделывается в рекурсивный алгоритм со временем работы . Код на Python:
def josephus(n, k): return 0 if n == 0 else (josephus(n - 1, k) + k) % n
Ещё более быстрый алгоритм
Оказывается, что для частного случая, когда , можно построить ещё более быстрый алгоритм! Опять же, мы настоятельно рекомендуем вам попробовать придумать его самостоятельно. Решение можно найти в видео выше или в нашей интерактивной книге "Алгоритмические задачи с собеседований" (см. раздел 5.11, он доступен бесплатно; до 19 января действует промокод HABR, дающий скидку 40%).
