Это продолжение статьи про элементы теории хаоса с картинками. Современная теория хаоса — это большая и хорошо разработанная область математики, уже прочно вошедшая в набор современных инструментов естествознания. Многие результаты теории динамического хаоса, такие как странные аттракторы, бифуркационные диаграммы, фрактальные области притяжения, разобраны популяризаторами математики на плакаты, мемы и открытки. В этой мини‑серии статей я хочу копнуть немного глубже стандартных введений и «альбомов» с симпатичными картинками и дать пример разбора одной несложной, но ещё не «заезженной» механической системы, которая демонстрирует механизмы возникновения хаоса в гамильтоновых системах.
Мы разбираемся с движением идеального шарика, свободно падающего и упруго отскакивающего от столика на линейной пружинке. Главное достоинство этой системы состоит в том, что она позволяет продемонстрировать основные приёмы анализа хаотических систем, а главное, сделать видимыми возникающие при этом неочевидные математические структуры: инвариантные торы, резонансные циклы и разрушающиеся гомоклинические многообразия. Обычно в книгах и статьях их изображают схематично, здесь же у нас есть возможность увидеть их «истинный» облик.
В первой части мы увидели, какими необычно сложными могут быть подскакивания шарика над столиком с пружинкой. Движение самих тел достаточно тривиально, а вот их упругие соударения оказались способны производить красивую динамику, как упорядоченную, так и хаотичную. Рекомендую, если не прочитать первую часть, то хотя бы полюбоваться иллюстрациями, чтобы понять что именно мы будем объяснять на этот раз.
В физике под динамикой понимают движение некоторых тел или среды под действием сил, а более общем смысле — изменение состояния системы с течением времени. В математике понятие динамики ещё более абстрактное: это действие непрерывного гладкого отображения на некоторое гладкое многообразие. В нашем случае, многообразие — это пространство всех возможных состояний системы шарик-столик, которое описывается координатами и скоростями обоих тел, а действует на него отображение , заданное очень простыми уравнениями движения:
Здесь — безразмерные координаты шарика и столика,
— их скорости, а точки обозначают производные по времени. Третья строчка определяет условие упругого соударения при котором происходит обмен импульсами между шариком и столиком и заключает в себе нелинейность задачи.
Для того чтобы избежать необходимости работать в четырёхмерном фазовом пространстве и исключить явную зависимость от времени, мы сосредоточились на моментах соударений наших тел, когда
. Так от отображения
, непрерывного во времени, мы перешли к дискретному отображению
а потом упростили и его до отображения:
которые называются отображениями Пуанкаре. Последнее отображение образует динамику на двумерной сферической поверхности, задаваемой законом сохранения энергии системы:
Здесь — это полная энергия системы. Это единственный параметр задачи, который определяется еë начальными условиями: начальной высотой и скоростью шарика и столика. Поскольку система консервативна (гамильтонова) энергия не изменяется и может служить параметром.
Замечание для тех, кто в теме
Как правило, при анализе гамильтоновых систем, рассматривают некоторую интегрируемую систему и вводят малое возмущение, из-за которого возникают нелинейные эффекты и хаос. Из-за упругих столкновений наша система интегрируема только в тривиальном случае — в покое, так что и выполняет роль параметра возмущения.
Таким образом, от уравнений движения мы перешли к дискретному отображению , которое порождает последовательности соударений — орбиты отображения, и однозначно определяется единственным свободным параметром задачи
. Семейства орбит, как выяснилось, могут выглядеть неожиданно красиво. На рисунке показан пример такого семейства для
, изображенный в азимутальной проекции (детали построения такой проекции, смотрите в первой части).

Физическая симметрия задачи нашла отражение в симметрии фазового пространства и системы орбит. На азимутальной проекции выделяется зеркальная симметрия, с осью проходящей через начало координат и включающая в себя меридианы и
(зелёная линия на рисунке). Напомню, что таким образом проявляется симметрия обмена скоростями при упругом соударении одинаковых по массе тел.
Путешествие вокруг полюса
Перед тем как приступать к исследованию хаоса, нам нужно детально рассмотреть все возможные типы регулярных орбит отображения , их физический смысл и общую структуру. Эта часть рассказа необходима для того, чтобы познакомить нас с главными персонажами в гамильтоновом сценарии перехода к хаосу: полюсами и седловыми точками, эллиптическими и гиперболическими циклами, а также с инвариантными торами и гетероклиническими многообразиями.
Неподвижные точки
В прошлый раз мы отметили, что отображение является гомеоморфизмом — непрерывным отображением сферической поверхности в себя. Существует топологический факт, известный как теорема Брауэра:
Любое непрерывное отображение замкнутого шара в себя в конечномерном евклидовом пространстве имеет неподвижную точку.
Из этой теоремы следует, что обязана существовать как минимум одна точка, которую отображение возвращает в саму себя, то есть, неподвижная точка отображения Пуанкаре. По крайней мере, одну такую точку мы знаем: это точка со сферическими координатами
Ей соответствует состояние покоя системы в равновесии.
Давайте поищем другие неподвижные точки преобразования . В силу симметричности системы орбит преобразования, его неподвижные точки могут либо лежать на нулевом меридиане, либо располагаться зеркально относительно неё. Однако во втором случае обмен скоростями при ударе должен перевести любую такую точку в её зеркальное отражение, а значит, ни одна из них не останется неподвижной. Если мы ищем точки, переходящие сами в себя при зеркальном отражении относительно нулевого меридиана, то значит, все они должны лежать на нём.
Для того, чтобы найти все такие точки, вычислим расстояние между исходными точками нулевого меридиана и их образами:

Видим, что нулю это расстояние равно только в точках равновесия , и в точке
, выглядящей как полюс вокруг которой располагаются всё прочие орбиты. Других неподвижных точек в системе нет.
Точке соответствуют абсолютно правильные периодические подпрыгивания шарика, в которых в точности повторяются и координата соударения и скорости тел, равные друг другу по модулю в момент удара.

Полюс и его окрестности
Точка окружена сплошными кольцеобразными орбитами-спутниками. Давайте рассмотрим её окрестности подробнее:

Происходящее очень похоже на фазовый портрет для колеблющегося маятника. Это значит, что если немного «промазать» мимо неподвижной точки то должны наблюдаться своего рода колебания вокруг неё. Рассматривать физические траектории тел тут смысла мало, наш глаз не заметит разницы. Вместо этого, мы прибегнем к математическому анализу.
В прошлый раз мы подметили гладкость отображения , это значит, что его можно воспринимать, как гладкую вектор‑функцию и, следовательно, раскладывать в степенные ряды. Давайте рассмотрим линейное приближение отображения вокруг неподвижной точки. Для обыкновенной функции
еë линейное поведение около неподвижной точки
выглядело бы как прибавление к неподвижной точке величины
:
Для нашего отображения, как для функции над векторами, линейное поведение около неподвижной точки будет выражено очень похожим образом, но вместо прибавления числовой величины, мы будем немного смещаться от исходной точки на малый вектор , а образ смещения будет выражаться новым вектором
:
Смещение образа можно выразить, как результат действия на некоторой матрицы
. Она называется матрицей Якоби или якобианом отображения и представляет его линейное приближение в некоторой точке, подобно тому, как производная
является линейным приближением функции
. Собственно, якобиан и вычисляется через частные производные от компонентов вектор-функции, но, увы, нам неведомо явное выражение для
, мы знаем только алгоритм его вычисления. Однако, гладкость этого отображения позволяет нам вычислять производные численными методами.
Чтобы понять, что происходит с фазовым пространством вокруг точки , посмотрим как действует отображение
на два небольших ортогональных вектора, исходящих из неё.
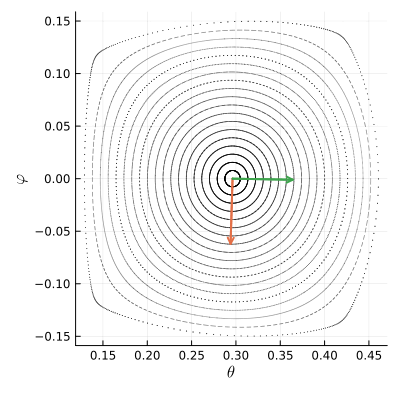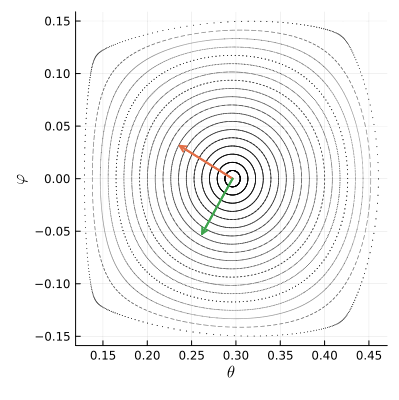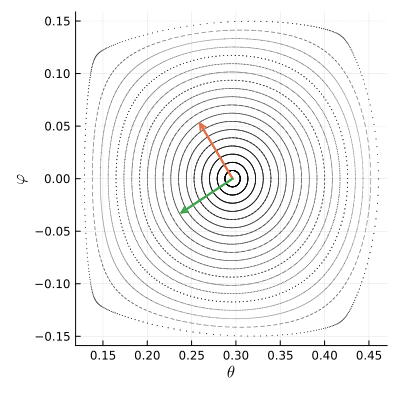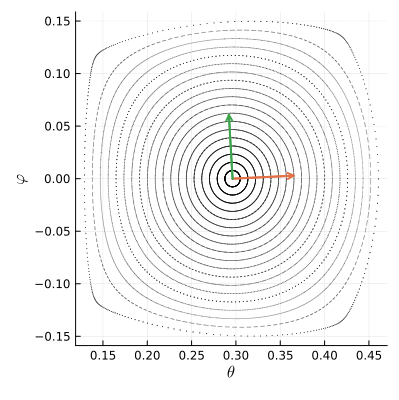
Как видим, отображение поворачивает векторы по часовой стрелке на четверть оборота и ещё чуть-чуть доворачивает. Численное вычисление производных в неподвижной точке показывает, что на малые векторы действует такая матрица Якоби:
Важную информацию о преобразовании несут определитель и спектр матрицы Якоби, то есть множество её собственных чисел. Определитель якобиана показывает, как под действием преобразования меняется площадь фигур. Для полученной нами матрицы он равен единице. Это значит, что преобразование сохраняет объём фазового подпространства, в котором мы работаем. Собственные числа якобиана получились комплексными: и их модуль тоже равен единице. Всё это говорит о том, что в точке
отображение
ведёт себя, как поворот, не изменяющий объёма пространства вокруг неподвижной точки.
Угол поворота, который совершает окрестность полюса под действием отображения, можно вычислить через аргумент собственного числа якобиана, в нашем случае он оказывается равным — те самые четверть оборота и ещё чуть-чуть, что мы наблюдали в эксперименте. Неподвижные точки, вокруг которых происходит вращение пространства, называют полюсами или эллиптическими точками. Собственные числа якобиана в таких точках должны лежать на единичной комплексной окружности, и иметь ненулевую мнимую часть.
Циклы и седловые точки
На портрете отображения видны и другие семейства концентрических эллиптических орбит, которые тоже образуются вокруг некоторых особых точек. Эти точки неподвижны для отображения , применённого несколько раз. Яркий тому пример дают четыре крупные кольцевые структуры, расположенные вокруг полюса
. Вот как они выглядят вблизи:

Точки, обозначенные на рисунке, как , под действием отображения
переходят друг в друга по очереди. При этом отображение
переводит каждую из них в саму себя. Такие точки образуют периодические орбиты или циклы. Полюсы, составляющие цикл конечной длины
мы будем называть полюсами
-ного порядка и обозначать
В том, что это именно полюсы можно убедиться, вычислив спектр якобиана от для них (они комплексные, лежат на единичной окружности и их аргумент соответствует повороту на
либо наблюдая действие этого отображения на малые векторы.
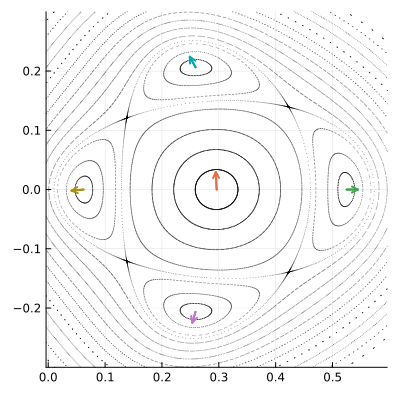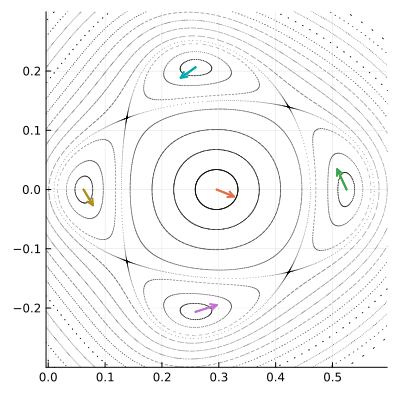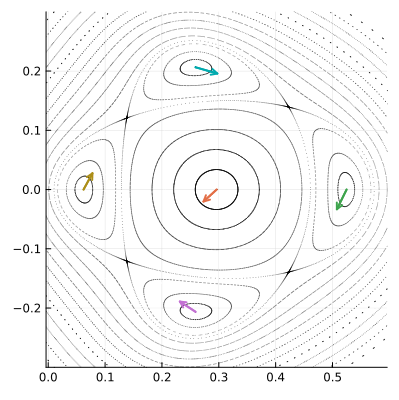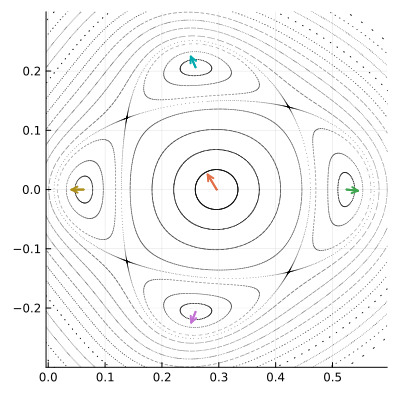
Однако несколько полюсов не могут размещаться рядом, не смыкаясь орбитами-спутниками. В какой-то точке эти орбиты должны будут соприкоснуться. Мы говорили, что в автономных системах, типа нашей, фазовые траектории пересекаться не могут, за исключением особых случаев. Это как раз такой случай. Особые точки, в которых разные орбиты пересекаются, тоже будут неподвижными для , они называются седловыми или гиперболическими точками. Мы будем обозначать их
. Показанные на рисунке точки
тоже образуют цикл четвёртого порядка, но он существенно отличается от цикла, образованного полюсами, динамикой фазового пространства в окрестности составляющих его точек.
Давайте исследуем их локальное поведение, наблюдая за тем, как отображение действует на два малых ортогональных вектора, исходящих из точки пересечения орбит, вдоль их касательных.
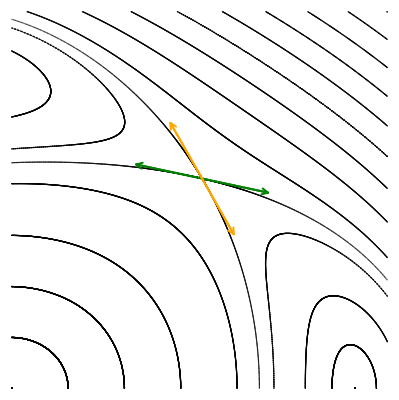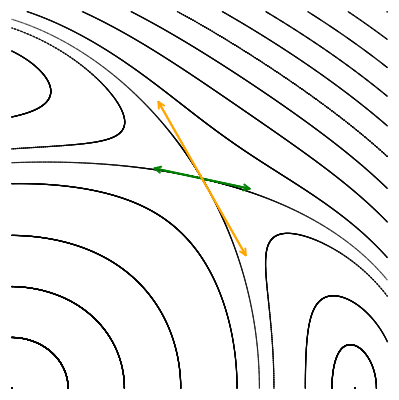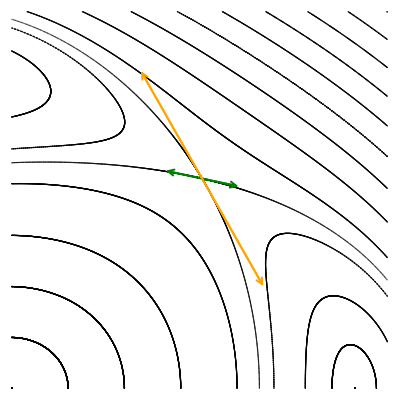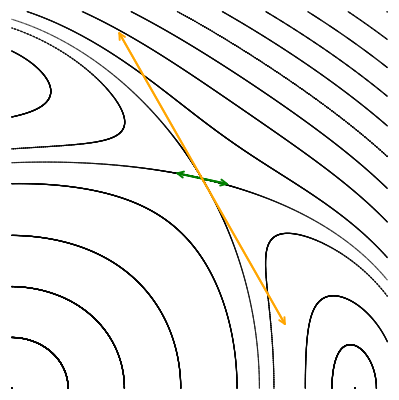
Мы видим, что по действием отображения Пуанкаре векторы не поворачиваются, а меняют свою длину: одна пара вытягивается, а другая сжимается. Выбранные нами направления совпадают с направлением собственных векторов якобиана в гиперболической точке. Действие матрицы на собственный вектор выражается только в умножении его на собственное число, без всякого поворота. Это значит, что собственные числа якобиана гиперболической точки должны быть вещественными. Причём наблюдаемая нами динамика говорит о том, что одно собственное число по модулю должно быть больше единицы (вектор удлинняется), а другое — меньше единицы, соответствующий собственный вектор укорачивается.
Для седловой точки при
якобиан получилcя таким:
с собствеными значениями: Примечательно, что для нашей системы определитель якобиана в этой точке равен единице, также как и в полюсе. То есть, не смотря на существенное искажение окрестностей фазового пространства, гиперболическое поведение не изменяет никакие площади.
Таким образом, мы приходим к важному заключению: циклы могут состоять либо из полюсов, либо из гиперболических точек. В первом случае орбита будет находиться в цикле или в его окрестности неограниченно долго. Такие устойчивые циклы мы назовём эллиптическими. Во втором случае при сколь угодно малом отклонении от седловой точки орбита покинет еë и вернется обратно, только пройдя по некоторой замкнутой линии, удаляясь от от исходной точки очень далеко. И седловые точки и образуемые ими гиперболические циклы являются неустойчивыми.
Инвариантные торы
А из чего состоят многочисленные орбиты, окружающие наши особые точки? Они выглядят, как сплошные замкнутые линии, можно ли воспринимать их как циклы очень высокого порядка? Для того чтобы понять, что же эти орбиты собой представляют, нам надо вернуться в четырёхмерное фазовое пространство . Исследуемое нами дискретное отображение
получается сечением непрерывных траекторий гиперплоскостью
в которой лежат точки соударения.
Давайте посмотрим как выглядит фазовая траектория для неподвижной точки в подходящем сечении четырёхмерного фазового пространства:

Это петля, которая встречает сечение Пуанкаре в неподвижной точке, потом покидает сечение и вновь возвращается к нему. А вот как выглядит фазовая траектория для цикла четвёртого порядка:

Обе траектории представляют собой нормальные замкнутые петли. Теперь построим траектории, соответствующие орбитам-спутникам этих неподвижных точек:


Мы видим, что полученные траектории «наматываются» на поверхности похожие на трубку, а сечение Пуанкаре вырезает на этой поверхности замкнутые кольцеобразные орбиты. Эти трубки особым образом замыкаются и образуют тор, внутри которого располагается петля цикла.
Обычно, говоря о торе, мы воображаем поверхность бублика. Чтобы получить из привычного тора наш вариант, нужно разрезать его и склеить, допустив самопересечение, как показано на рисунке:

С точки зрения топологии такой тор ничем не отличается от привычного. Чтобы получить тор для окрестностей цикла четвёртого порядка, его надо разрезать и переклеить четыре раза. Полюбуйтесь как выглядит небольшое семейство таких тороидальных трубок:

В отличие от циклов, траектории, образующие торы, не замкнуты и плотно заполняют тороидальную поверхность, не оставляя на ней ни одной точки, через которую не проходила бы траектория. Это значит, что в качестве решения задачи имеет смысл рассматривать весь тор сразу. Поскольку все его точки принадлежат одной бесконечной траектории, то исходная система уравнений переводит весь такой тор в себя. Таким образом, он является инвариантным многообразием динамической системы, а сечения тора — замкнутые орбиты, будут инвариантными многообразиями отображения Пуанкаре. Инвариантные торы называют также торами Колмогорова-Арнольда-Мозера, или КАМ-торами.
Теперь мы готовы исчерпывающе описать регулярную структуру фазового пространства задачи. Оно плотно заполнено одномерными замкнутыми петлями, и двумерными инвариантными торами, которые образуют расслоение пространства. Фазовое пространство отображения Пуанкаре, в свою очередь, содержит одномерные полюсы и седловые точки, образующие циклы, и расслаивается одномерными инвариантными многообразиями, которые мы тоже будем называть КАМ-торами.
Кроме перечисленных выше и хаотических, иных орбит в гамильтоновых системах нет. Так что рассмотреd все типы инвариантных многообразий и для нашего прыгающего шарика, мы познакомились со всем, что может встретиться и во всех других гамильтоновых механических системах: бильярдах на кривом столе, двойном или эластичном маятнике, в динамике атмосферы Юпитера или колец Сатурна.
Гидродинамика инвариантных торов
«Инвариантный» означает — неизменный. В нашем случае, речь идёт о том, что под действием уравнений движения одни точки этих многообразий переходят в другие, но при этом само многообразие (тор или петля) не изменяется и отображается уравнениями движения в себя. Таким образом, мы можем не заботиться о начальных условиях и рассматривать судьбу и свойства инвариантных многообразий, как неделимых объектов. То же относится и к орбитам отображения Пуанкаре: неподвижным точкам и сечениям КАМ‑торов.
Как мы увидели, в середине любого инвариантного тора "живёт" полюс, вокруг которого происходит вращение фазового пространства. Это значит, что точки торов, плотно заполняющих это пространство, сами тоже должны вращаться, оставляя сами торы на месте. На это движение моожно посмотреть.

Обратите внимание, на каждом торе скорость движения точек своя, немного отличающаяся от скорости движения на соседнем торе. Это важное наблюдение подводит нас к неожиданной аналогии с движением сплошной среды.
В течении жидкости или газа на дозвуковых скоростях важную роль играет неразрывность среды. Она приводит к непрерывности и гладкости поля скоростей: у частиц, движущихся вдоль близких линий тока скорости тоже должны быть близки, а в пределе они должны гладко приходить друг к другу.
Если по какой-то причине наблюдается разрыв в скоростях соседних линий тока, то течение становится неустойчивым. При этом на границе развиваются волны, быстро превращающиеся в дорожку из вихрей, которые вращаясь, сглаживают разрыв, как подшипники. Этот механизм называется неустойчивостью Кельвина-Гельмгольца и наблюдается в жидкостях и газах

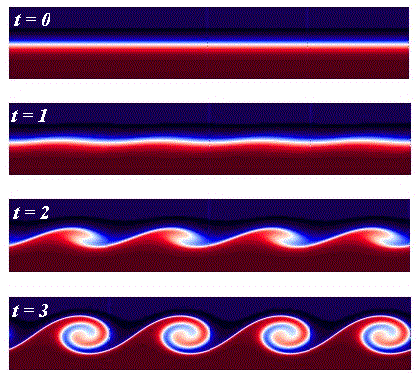


Отображение Пуанкаре для нашей задачи имеет мало общего с гидродинамическим потоком: в нём нет инерции или давления. Объединяет эти два объекта только непрерывность поля скоростей и малые потери энергии (гамильтоновость). Эти ключевые характеристики приводят к тому, что они способны порождать подобные геометрические структуры.
Можно построить непрерывное поле скоростей, образованное инвариантными торами и увидеть, что при приближении к окрестностям неподвижных гиперболических точек движение орбит по разные стороны от седла происходит в противоположные стороны:

Более того, это движение приводит к растяжению и сжатию пространства вдоль собственных векторов, которое мы наблюдали в окрестности седловой точки. В то же время, движение вокруг полюсов четвёртого порядка согласуется с общим движением потока и подобно вихрям Гельмгольца выполняет роль «подшипников», вращающихся без проскальзывания между внутренней областью, вращающейся по часовой стрелке, и внешней, которая вращается в противоположном направлении.
Получается, что по какой‑то причине в поле скоростей инвариантных торов образуется разрыв. Но поскольку непрерывность — ключевое свойство этого поля, то в нём формируется система из чередующихся полюсов и седловых точек, обеспечивающих сохранение этого свойства. Если вы ещё раз присмотритесь к тому, как развивается неустойчивость Кельвина-Гельмгольца, то без труда найдёте в течении невидимые седловые точки, которые легко распознаются по гиперболическому характеру поля скоростей вокруг них.
Ещё раз подчеркну: аэродинамические вихревые дорожки и инвариантные торы отображения Пуанкаре — явления абсолютно разной природы. Первое может служить аналогией второму только вследствие общих свойств гладких непрерывных преобразований. Это хорошо известное явление конвергенции, когда разные процессы приводят к одинаковым геометрическим формам. Ровно такие же паттерны и соображения вы можете встретить в теории полей, в решениях однородных дифференциальных уравнений, в теории аналитических функций, в общей топологии, везде, где непрерывность играет существенную роль. В этом и состоит очарование и сила математики!
Сходство динамики инвариантных торов и гидродинамических вихрей, естественно привлекло внимание механиков, исследовавших явление турбулентности и переход от ламинарного (слоистого) течения, в котором силы вязкости существенно превышают силы инерции, к когерентным структурам (крупных вихревым дорожкам) и потом к развитой турбулентности и к хаосу, когда система становится гамильтоновой и вязким трением на крупных масштабах можно пренебречь. Одними из первых, кто решил, что в динамике инвариантных торов можно найти сценарий перехода были А. Пуанкаре, Л. Ландау и А. Колмогоров. Однако позже, с дальнейшим развитием теории хаоса, стало ясно, что динамика инвариантных многообразий может служить лишь триггером к более сложным динамическим процессам — сценарию Рюэля и Такенса, диффузии Арнольда и другим явлениям.
Числа вращения и резонансы
Но что же останавливает вращение инвариантных торов? И почему для это привело к образованию двух циклов именно четвëртого порядка?
Существование неподвижных точек позволяет торам сменить направление вращения без нарушения непрерывности поля скоростей, но ценой образования дополнительной структуры: цепочки полюсов, окружённых замкнутыми орбитами, и раздёляющих их седловых точек. Но откуда берётся эта смена направления?
С точки зрения топологии, тор представляет собой произведение двух окружностей: Или, менее формально, это поверхность вращения, получаемая при движении окружности вокруг некоторой внешней оси. Под окружностями в топологии понимается произвольная замкнутая петля, а не только та правильная геометрическая фигура, которую мы проходили в школе. Поскольку тор мы понимаем достаточно обобщённо, вместо образующих его окружностей имеет смысл рассматривать две оси, которые охватывают эти петли: внутреннюю и внешнюю.
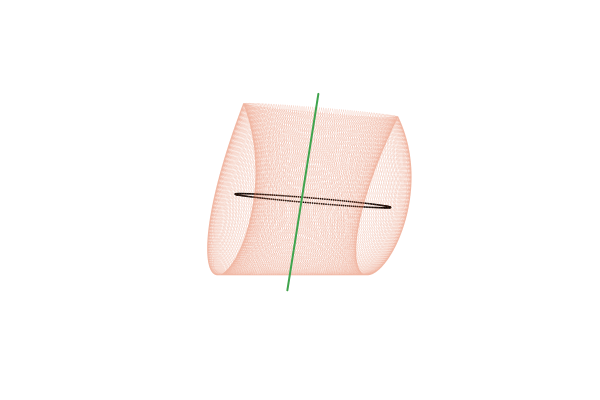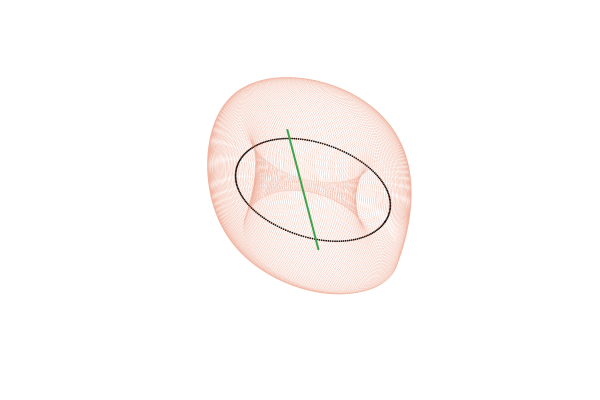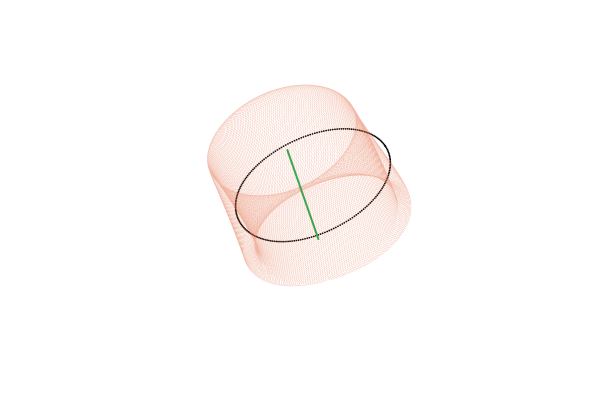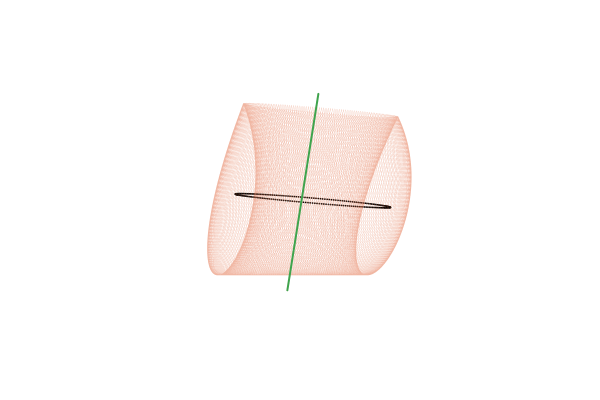
рассчитанных для
Действие отображения на инвариантный тор можно представить как композицию двух смещений вдоль образующих его петель. При этом в сечении Пуанкаре мы видим смещение только по одной из них, которое и воспринимаем как движение, похожее на вращение. По второй образующей фазовая траектория проходит во время между моментами пересечения плоскости
, то есть, между столкновениями шарика и столика. Таким образом, траектория отображения
как бы наматывается на тор по винтовой линии, как показано на рисунке:
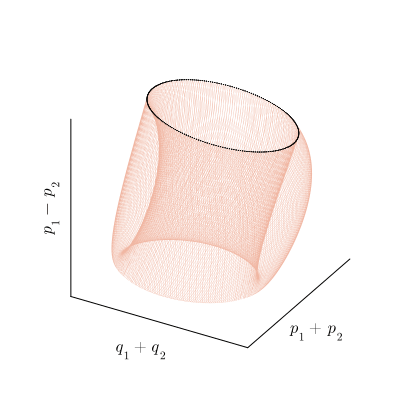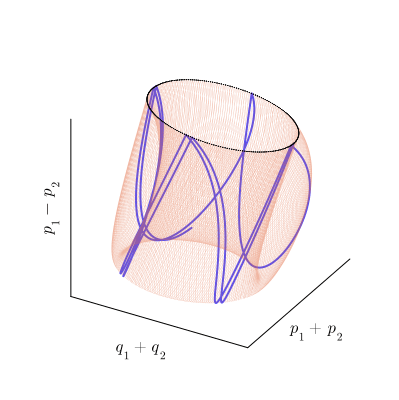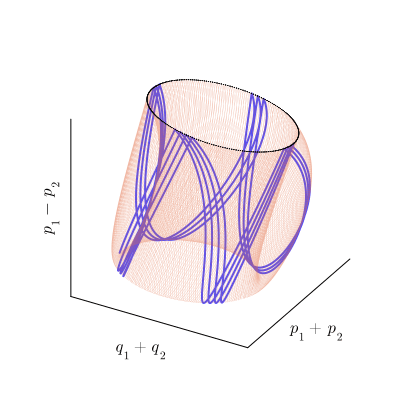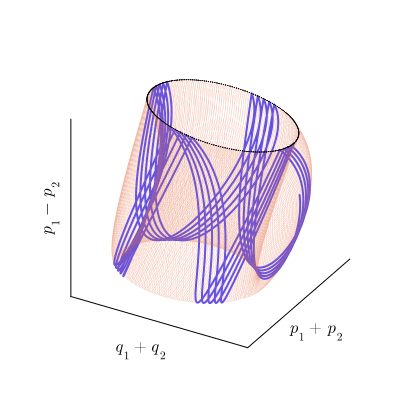
По мере этого наматывания, траектория совершает обороты вокруг обеих осей тора. Мы можем подсчитывать число оборотов, совершаемых траекторией вокруг каждой из осей тора и вычислять соотношение, показывающее сколько оборотов вокруг внутренней оси приходится на один оборот вокруг внешней. Это число называется числом вращения инвариантного тора. Обратите внимание на то, что эта числовая характеристика является чисто топологической и не меняется при непрерывных искажениях тора, так что ни его форма, ни форма траектории, ни параметризация траектории по времени не играют никакой роли. Это делает число вращения характеристикой, однозначно определяемой для каждого инвариантного тора.
И тут возможны два качественно разных варианта.
Число вращения иррационально. В этом случае фазовая траектория никогда не замкнëтся и плотно заполнит всю поверхность инвариантного тора.
Число вращения рационально и выражается дробью
. В этом случае фазовая траектория, совершив
оборотов вокруг внутренней оси, сделает ровно
оборотов вокруг внешней оси тора, и должна замкнуться. Такой случай называется резонансом. При этом движение вдоль сечения по петле, окружающей внутреннюю ось, останавливается, инвариантный тор разрушается и превращается в одномерную замкнутую траекторию, а еë сечение Пуанкаре — в цикл.
Получается, в разрушении инвариантных торов и в появлении всех нетривиальных циклов повинны резонансы — рациональные числа вращения. Непрерывность отображения приводит к непрерывности поля смещений фазового пространства, которое они образуют. А в непрерывном поле скоростей неподвижные точки цикла должны образовывать цепочку полюсов и седловых точек, формируя эллиптический и гиперболический циклы. Порядок циклов на которые распадается резонансный инвариантный тор, определяется его числом вращения, а именно, его знаменателем.
Например, тор с числом вращения распадëтся на две замкнутые траектории (устойчивую и неустойчивую), каждая из которых перед тем как замкнуться, совершит 4 оборота вокруг внутренней оси и один оборот вокруг внешней. Эти петли создадут восемь неподвижных точек четвёртого порядка в сечении Пуанкаре: четыре полюса и четыре седловые точки. При этом эллиптическая замкнутая траектория станет внутренней осью для семейства новых инвариантных торов.

На поле скоростей мы наблюдали ещё одну примечательную особенность: смену направления вращения инвариантных торов по разную сторону от распавшегося резонансного тора. Этой смене можно дать красивое объяснение, сравнив резонанс инвариантного тора с резонансами в стробоскопическом эффекте. Вспомните, как в кино движутся спицы вращающегося колеса. Давайте посмотрим на этот эффект в чистом виде, «вращая» одну спицу с разной скоростью и с фиксированной частотой смены кадров.

По мере замедления частоты вращения спицы, начинают появляться резонансы третьего, четвёртого, пятого и больших порядков. При переходе через резонанс небольшие «перелëты» сменяются небольшими «недолëтами» картинки между кадрами, видимое движение замедляется, останавливается и меняет направление. Точно такой же эффект наблюдается и в динамике инвариантных торов.
Структура циклов
Взгляните ещё раз на карту орбит системы при . Мы отчётливо видим карте орбит циклы небольшого порядка: четвёртого, пятого, шестого. Между ними проявляются цепочки овальных орбит, окружающих циклы более высоких порядков. Есть ли какая-то закономерность в их расположении? И почему мы не видим циклов второго и третьего порядков?
Мы связали возникновение циклов и рациональностью числа вращения инвариантного тора. Как известно, рациональные числа образуют плотное множество, это значит, что между любыми двумя такими числами на числовой прямой обязательно найдëтся третье, а следовательно, и четвëртое с пятым и, вообще, сколько угодно чисел. Получается, резонансные торы, распадающиеся на циклы, должны встречаться повсюду и в неограниченном количестве, плотно заполняя фазовое пространство. Однако, с другой стороны, множество иррациональных чисел на этой же числовой прямой образует континуум, который настолько мощнее множества рациональных чисел, что вероятность наугад выбрать рациональное число из отрезка числовой прямо стремится к нулю. Так что случайно попасть на резонансный тор, выбирая точки фазового пространства, практически невозможно, и следовательно, мы должны наблюдать преимущественно не разрушенные, сплошные торы, окружающие либо полюс , либо какие-то полюсы более высокого порядка. В экспериментах мы видим что-то среднее: несколько ярко выраженных резонансов низкого порядка, которые проявляются в виде деформации многочисленных инвариантных торов с иррациональными числами вращения.
Дело в том, что непрерывность отображения приводит к непрерывности поля скоростей вращения инвариантных торов, а это, в свою очередь, делает непрерывным и отображение между торами и их числами вращения. Таким образом, при непрерывном переходе от тора с резонансом
до тора с резонансом
, мы должны пройти по непрерывному отрезку чисел вращения в интервале от
до
Чем больше оказывается знаменатель у числа вращения цикла, тем больше его порядок и тем более плотную цепочку полюсов и седловых точек он образует. Циклы с порядком больше 20 мы уже воспринимаем, как тонкую пунктирную линию и с трудом отличаем от нерезонансных инвариантных торов. Так что заметно выделяются среди сплошных орбит только циклы небольших порядков.
Отсюда мы приходим к вопросу теории чисел о взаимном расположении дробей с наименьшими знаменателями. Для указанных двух дробей найти дробь, лежащую между ними, имеющую наименьший возможный знаменатель позволяет операция, которая называется медиантой и является одним из корректных способов вычисления среднего значения:
Для всего множества рациональных чисел можно построить иерархию дробей по знаменателям, согласованную с отношением порядка на числовой прямой, которое называется деревом Штерна-Броко. Я уже рассказывал немного об этом здесь.
Например, между резонансами и
могут лежать только торы, с числами вращения в диапазоне от
до
. Дробь с наименьшим знаменателем получаем, как медианту
следовательно, между этим двумя резонансами будет наблюдаться цикл с наименьшим периодом, равным девяти. Строя дерево Штерна-Броко для этого интервала, мы получаем взаимное расположение резонансов


Теперь становится понятным, почему около крупных структур, образуемых циклами малых порядков, мы наблюдаем исключительно сплошные линии орбит — чем ближе мы подходим к рациональному числу, тем большие знаменатели будут иметь резонансы.
Мы в состоянии объяснить также почему мы не видим циклов второго и третьего порядков. Дело в том, что вокруг полюса отображение
действует, как поворот фазового пространства на угол чуть больше четверти полного оборота — на
Это задаëт предельную величину для чисел вращения торов, окружающих
приблизительно равную
то есть, лишь немного отличающуюся от
. А между
и этим числом не располагаются ни
ни
всё они существенно больше.
А есть ли какая-то нижняя граница на числа вращения инвариантных торов? Отображение имеет неподвижную точку p⁰, которая является вырожденным узлом и в окрестности которой движение торов останавливается. Следовательно, торы по мере приближения к линии экватора , будут замедлять скорость движения до остановки, а их резонансы будут иметь всё большие и большие знаменатели, и нижней границей является
Таким образом, используя закономерности расположения рациональных чисел на числовой прямой, мы можем дать исчерпывающее качественное и количественное описание структуры всех циклов в нашей системе. Все резонансы будут располагаться в соответствии с деревом Штерна-Броко на интервале от до предельного числа вращения, соответствующего скорости вращения полюса
, которая, в свою очередь, вычисляется, как отношение аргумента собственных чисел якобиана в полюсе к
При увеличении энергии, предельное число вращения будет увеличиваться. Вот как выглядит эта зависимость:

При станет возможно появление цикла 5-го порядка, а цикл 4-го порядка появится уже при
Особый интерес представляет рождение резонанса с циклом вращения
, которое происходит при
. При этом полюс перестаёт быть полюсом и превращается в седловую точку. Это явление называется бифуркацией удвоения периода, при котором устойчивая неподвижная точка
превращается в неустойчивую и порождает новый устойчивый цикл
Более подробно об этой бифуркации мы поговорим позже, она является одним из механизмов появления хаоса в нашей системе. А пока, вернёмся к упорядоченным стуктурам и посмотрим, как периодические орбиты выглядят на карте для
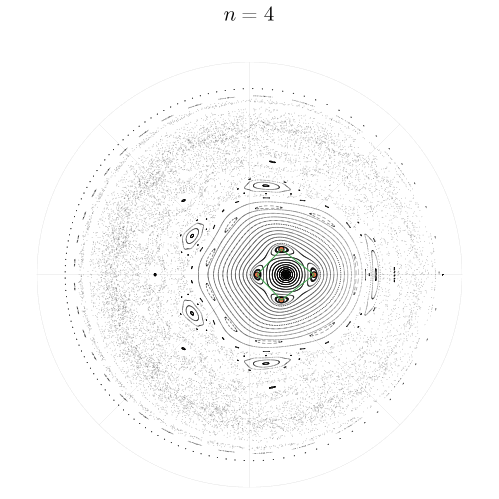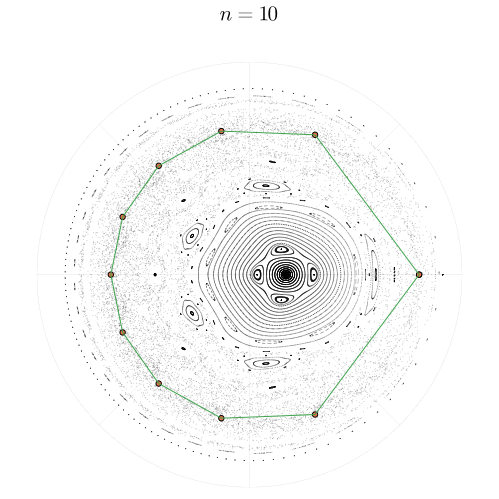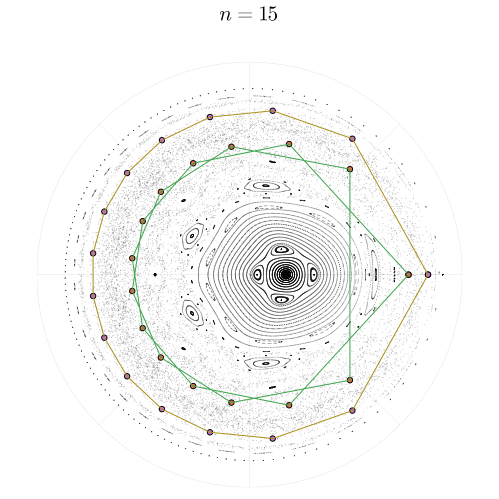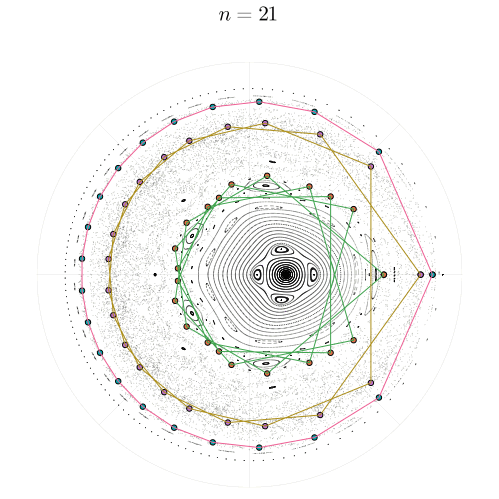
Если внимательно просмотреть все двадцать примеров, то можно обратить внимание на то, как перед тем, как замкнуться, цикл порядка может совершить
оборотов вокруг полюса
, что является хорошей демонстрацией резонансного числа вращения
Циклы, по-видимому, существуют как в упорядоченной, так и в хаотической области. Неужели они способны сохранить устойчивость в море хаоса? Это можно определить, вычислив собственные числа якобиана в неподвижных точках. Рассмотрим, например, циклы с числами вращения и
Вот спектры якобиана для этих случаев:
Получается, что цикл из эллиптического превратился в гиперболический, тогда как цикл
остался устойчивым. Это говорит о том, что хаотическая область, поглощая цикл, каким-то образом разрушает его. Но, как мы увидим, напротив, это циклы в ходе своей эволюции порождают хаос.
Источники хаоса
В теории динамических систем важную роль играет понятие структурной устойчивости, которое относится к динамическим системам в целом, а также к их особенным точкам, инвариантным многообразиям и к поведению фазового пространства вокруг них.
Например, в гамильтоновых системах структурно устойчивы полюсы, поскольку небольшие изменения параметров системы могут изменить их положение в фазовом пространстве, скорость вращения в их окрестностях, но оставляют их полюсами. Исчезнуть или появиться они могут только в результате особого явления: бифуркации — скачкообразной качественной перестройки структуры системы при плавном изменении еë параметров. Однако бифуркация в пространстве параметров это объект нулевой меры, то есть, граница между областями, в которых структурная устойчивость сохраняется.
Структурная устойчивость седловых точек проявляется в том, что при изменении параметров могут меняться собственные значения якобиана и направления собственных векторов, но это меняется гиперболическая природа седловой точки и она остаëтся локально неустойчивой неподвижной точкой. Также структурно устойчивы инвариантные торы и резонансные цепочки: возмущения их деформируют, но оставляют самими собой.
Важный пример структурно неустойчивого многообразия — особая орбита, соединяющая две седловые точки, которая называется гетероклиническим многообразием. Оно не имеет топологии тора, для него неприменимо понятие числа вращения, вообще, как мы увидим, это довольно своеобразный объект. Вот пример такого многообразия, возникающего при появлении в нашей системе резонанса четвёртого порядка.
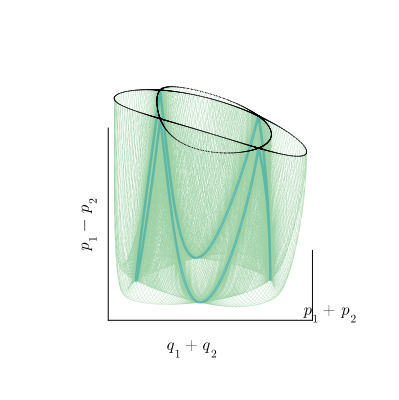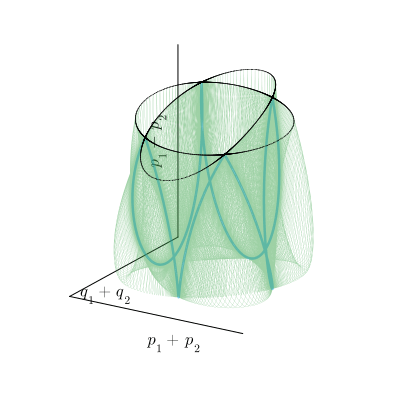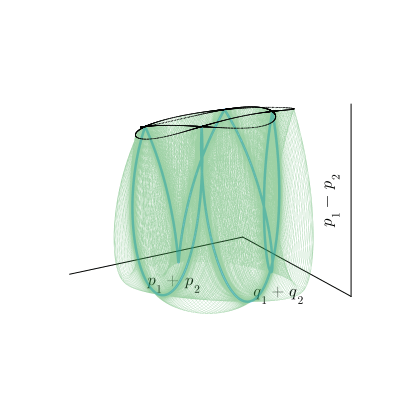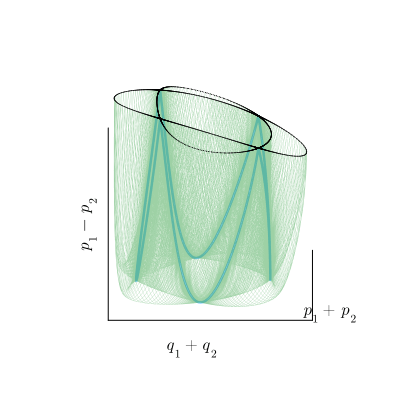
К счастью, нам не потребуется сложное трёхмерное представление этого многообразия, поскольку всеми его свойствами обладает двумерное сечение Пуанкаре.
Мы неоднократно упоминали, что в автономных системах фазовые траектории не пересекаются. Гетероклинические орбиты являются исключением: в седловых точках они пересекаются под ненулевым углом. При этом каждая из них одновременно является неустойчивым инвариантным многообразием для одной седловой точки и устойчивым многообразием для другой. Обозначим эти многообразия и
соответственно, а само гетероклиническое многообразие образованное седловыми точками
обозначим как
.

В отличие от торов, движение вдоль занимает бесконечное время: точки экспоненциально быстро удаляются от одной неподвижной точки вдоль
, но при этом к другой точке они приближаются вдоль
экспоненциально медленно. Таким образом, показанное на рисунке многообразие, хоть и является топологически связным, но с точки зрения динамики, распадается на восемь раздельных орбит, так что точка никогда не сможет перейти с одной орбиты на другую.
Структурная неустойчивость многообразия проявляется в том, что его существование возможно только в точке бифуркации, на границе между областями в пространстве параметров, в которых устойчивы другие объекты: инвариантные торы с одной стороны, и странные аттракторы с другой (о том, что это за звери, поговорим чуть позже).
Полное совпадение и
возможно только в отсутствии каких бы то ни было возмущений в системе, отклоняющих её от линейного полностью интегрируемого приближения. При наличии любого отличного от нуля возмущения, эти многообразия совпадать перестают.
Что такое «возмущение» в нашем случае? Это неизбежная нелинейность системы, связанная с ударами из‑за которых потенциальная энергия системы теряет гладкость. Динамика седловой точки состоит в одновременном растяжении и сжатии фазового пространства, с сохранением его объёма. И интенсивность этих деформаций зависит от энергии системы. Напомню, что резонансные циклы рождаются в окрестности неподвижной точки , при достижении некоторого значения энергии
. Это хороший пример бифуркации.
"Новорождённый" резонанс состоит из цепочки полюсов и седловых точек, но в момент рождения собственные числа якобиана во всех точках цикла должны совпадать с собственными числами полюса , которые располагаются на единичной окружности в комплексной плоскости. Дальнейшее увеличение энергии приводит к тому, что собственные числа якобиана седловых точек покидают единичную окружность, оставаясь на вещественной оси. Одно собственное число при этом становится больше единицы, а другое — меньше, в то время как их произведение (определитель якобиана) остаëтся единичным, так что они взаимно обратны. Вот как выглядит спектр якобиана типичной седловой точки:

Незначительное в начале, растяжение и сжатие фазового пространства вокруг седловой точки становится весьма сильным при увеличении энергии системы. Совпадение устойчивого и неустойчивого многообразий при этом нарушается. Собственные числа якобиана в точках являются основаниями геометрической прогрессии, которой подчиняются расстояния между точками на орбите
и неподвижными точками
Этот экспоненциальный характер растяжения и сжатия приводит к тому, что малое отклонение от
на расстояние порядка
увеличивается и достигает значений порядка единицы за время, пропорциональное
. Всë это приводит к тому, что вероятность для точки остаться на
под действием отображения
при энергии больше
стремится нулю.
Когда в системе есть трение или вязкость, то и
не совпадают и не пересекаясь, формируют спиралевидные структуры, как показано на рисунке:

Но в нашей системе трения нет, она консервативна, куда же деваться несовпадающим устойчивому и неустойчивому инвариантным многообразиям? Они больше не могут достичь седловой точки, но закончиться «просто так», или уйти в бесконечность они тоже не могут (вокруг полно инвариантных торов, с которыми пересекаться они не могут). Значит, эти многообразия должны каким‑то хитрым образом упаковываться в конечном объëме фазового пространства, оставаясь бесконечными.
В 1950 году Гаррет Биркхоф доказал общую теорему для двумерных систем, которую через 15 лет Стивен Смейл смог обобщить на системы любых размерностей:
Если для некоторого гладкого отображения
устойчивое и неустойчивое гетероклинические многообразия пересекаются под ненулевым углом, то должно существовать бесконечное множество таких пересечений, имеющее топологию канторова множества. При этом в любой окрестности любого такого пересечения найдутся периодические орбиты отображения
Доказательство теоремы Биркхофа‑Смэйла непростое и я не буду приводить его здесь. Вместо этого предлагаю посмотреть «под микроскопом» на то, как ведут себя гетероклинические многообразия вблизи седловых точек.
В качестве объекта исследования возьмём пару соседних седловых точек Разместим большое количество точек на многообразиях
и
очень близко к одной из них, так чтобы попадание на многообразия было максимально точным. Далее, будем применять к точкам, лежащим на
отображение
, а к тем, что лежат на
отображение
, то есть, обратное отображение Пуанкаре. Точки начнут медленно покидать окрестности нашей седловой точки и перемещаться к соседней, как поезд по рельсам. Там-то мы и поставим свой «микроскоп», дожидаясь приближения «поезда» около самой «конечной станции», и вот какую неожиданную картину мы увидим:

Устойчивое и неустойчивое многообразия, при приближении к седловой точке, оставаясь гладкими линиями, искривляются и превращаются в волны, которые сжимаются и вытягиваются, подчиняясь гиперболической динамике точки Именно эти волны образуют то самое бесконечное множество пересечений, о котором говорится в теореме Биркхофа-Смэйла.
Такое поведение не относится только к нашей системе, оно носит универсальный характер, так что в любой динамической системе появление гетероклинической орбиты приводит к образованию подобной структуры из бесчисленного множества петель, изгибов и меандров. Но что же собой представляет это сложное множество пересечений?
Странный аттрактор
Красивая картина складок гетероклинических многообразий, на самом деле, весьма тонкий эффект, который достаточно сложно наблюдать. Для этого мне пришлось использовать вычисления повышенной точности, начальные точки на многообразиях должны были располагаться очень близко к седловой точке и должны были идеально попасть на гетероклинические орбиты.
Если мы будем менее точны и понаблюдаем за динамикой небольшого шара в фазовом пространстве, окружающем седловую точку, то увидим, что в окрестности соседней седловой точки он будет многократно сложен в складки, потом растянут вдоль неустойчивого многообразия, а потом снова сложен и вновь растянут около другой седловой точки. Это преобразование — композиция растягивания и складывания называется преобразованием пекаря по аналогии с вымешиванием теста. Такое преобразование активно перемешивает фазовое пространство, так что изначально близкие точки экспоненциально быстро разбегаются друг от друга, но при этом всегда оставаясь заключены в некотором конечном объёме. В то же время, точки из разных объёмов фазового пространства оказываются через какое-то время рядом.
Не следует забывать, что мы рассмотрели поведение седловой точки пятого порядка, а это значит, что она "работает" не одна, а в компании четырёх себе подобных. Складки инвариантных многообразий не только растягиваются, покинув окрестность седловой точки, они разбегаются по разный её соседям: часть — налево, часть — направо, что ещё больше усиливает чувствительность к начальным условиям. В качестве примера, пронаблюдаем за тем, как перемешиваются окрестности двух разных седловых точек (по 50 тысяч чёрных и красных точек):

В первые моменты прекрасно видно, что точки следуют вдоль неустойчивых инвариантных многообразий, которые изгибаясь пересекаются и смешиваются, растягиваются и снова изгибаются. Несмотря на активнейшее перемешивание, преобразование пекаря имеет бесконечное множество неподвижных точек различного порядка. Совокупность этих неподвижных точек называется странным аттрактором.
Это необычная структура является глобально устойчивой (орбита не никогда покидает его), но состоит сплошь из локально неустойчивых циклов самого разного порядка. Так что расстояние между какими-либо двумя близкими точками, принадлежащими одному аттрактору будет экспоненциально быстро увеличиваться. Настоящим открытием Смейла было то, что динамическая система может устойчиво иметь бесконечное количество неустойчивых периодических орбит. Странный аттрактор является инвариантной структурой, но уже не может считаться многообразием, поскольку обладает топологией канторова множества, тогда как многообразие должно быть локально подобно евклидовому пространству.
Все примеры динамического хаоса (не только гамильтонового) заключают в себе те или иные странные аттракторы, которые имеют очень разнообразную природу, топологию и сценарии возникновения. Рассмотренный нами сценарий разрушения резонансных КАМ-торов из-за структурной неустойчивости гетероклинических орбит называется сценарием Рюэля-Такенса.
Хорошую демонстрацию чувствительности в начальным уловиям даёт попытка применить к действию большого числа итераций отображения столько же обратных отображений
. Наша система детерминистическая и консервативная, а это значит, что в идеале, точки должны сойтись обратно к начальным окрестностям. Однако, «фарш невозможно провернуть назад», точки сходятся, но не все.

Странный аттрактор, хоть и устойчив, хоть и сохраняет энергию системы, но способен безвозвратно утрачивать информацию.
Диффузия Арнольда
Итак, распад гетероклинической орбиты, приводит к тому, что седловая точка, сразу после своего появления окружает себя облаком странного аттрактора. Это облако немного расширено в непосредственной окрестности седловой точки и сильно вытянуто вдоль его устойчивого и неустойчивого многообразий, так что для малых энергий странный аттрактор практически совпадает с инвариантными многообразиями. В таких случаях говорят, что гетероклиническая орбита затеняет собой странный аттрактор.
Однако увеличение энергии системы увеличивает отклонение собственных чисел якобиана седловой точки от единицы. Это в свою очередь, усиливает растяжение и сжатие фазового пространства около этой точки и расширяет область в которой пересекаются её гетероклинические многообразия. По мере увеличения энергии системы, хаотическое облако постепенно расширяется, вовлекая в неопределённое поведение инвариантные торы на границе хаотической области. Это явление называется диффузией Арнольда.
Увидеть это явление непосредственно можно, наблюдая за тем, как с увеличением энергии системы расширяется проекция на нулевой меридиан орбиты, начинающейся в седловой точке.

Каждая седловая точка образует на этой диаграмме плавно расширяющийся конус, похожий на длинный коготь. В какой-то момент происходит объединение и перекрытие соседних конусов, это значит, что перемешивающее действие седловых точек полностью захватило стабильную область, лежавшую между ними и все точки в ней превратились в точки нового объединëнного странного аттрактора.
Впрочем, на диаграмме с диффузией Арнольда видно, что объединение конусов — это не единственный механизм, приводящий к расширению хаотической области. По мере увеличения энергии обширные хаотические области рождаются как-бы из ниоткуда. Его источником являются уже не седловые точки, а упомянутые выше бифуркации, приключающиеся с полюсами.
Отражение большого в малом
Давайте внимательнее присмотримся к полюсам, и исследуем их поведение. В прошлой части мы увидели, что полюсы, оказавшись в хаотической области, могут претерпеть бифуркацию удвоения периода, превратившись в седловую точку. В качестве примера рассмотрим подробно, как увеличение энергии сказывается на полюсе и собственных числах якобиана в нём.

По мере увеличения энергии, и полюс становится более «энергичным» — увеличивается скорость вращения фазового пространства вокруг него, о чём говорят увеличивающиеся углы собственных чисел якобиана. Когда они, путешествуя по единичной окружности, пересекают углы в рождаются резонансы инвариантных торов 5, 4 и 3-го порядков, точно также как это происходит в полюсе
Однако поскольку они рождены полюсом
порядки этих резонансов (знаменатели чисел вращения) будут равны 7×5 = 35, 7×4 = 28 и 7×3 = 21, соответственно.
Наконец, собственные числа полюса достигают угла , что приводит к рождению резонанса второго порядка. В этом случае появляется два полюса и только одна седловая точка. В силу симметрии, седловая точка этого резонанса оказывается ровно на месте полюса
в этот момент спектр якобиана этой точки покидает единичную окружность и переходит на вещественную прямую. Так в результате бифуркации один полюс теряет устойчивость, превращаясь в седловую точку, и одновременно с этим рождается пара новых устойчивых полюсов. Из новой седловой точки исходит два инвариантных многообразия, которые петлями возвращаются обратно, образуя «восьмёрку». Такие орбиты называются гомоклиническими и они незамедлительно порождают новый странный аттрактор по сценарию Биркхофа-Смэйла, описанному в предыдущем разделе.
Подобная судьба постигает все полюсы высших порядков, рождающихся в резонансах. Присмотритесь к резонансу третьего порядка, родившемуся из полюса Он в свою очередь также распадается на резонансы 5, 4, 3 порядков, достигает резонанса второго порядка, превращается в гомоклиническую восьмёрку и после этого красиво исчезает в облаке хаоса. Однако перед тем как исчезнуть, любой полюс проходит сквозь ещё одну красивую историю: через каскад бифуркаций удвоения периода, который приводит к хаосу через сценарий Фейгенбаума.
Полюсы, рождённые в результате удвоения периода, по мере увеличения энергии, тоже увеличивают свои числа вращения, которые достигают Однако, начинают они свою эволючию всё с больших и больших чисел вращения, так что бифуркации случаются всё чаще и чаще, образуя сходящуюся последовательность (она называется последовательностью Фейгенбаума). Вместе с тем, после каждой бифуркации количество полюсов удваивается, образуя возрастающую геометрическую прогрессию. При приближении к пределу последовательности точек бифуркации, количество циклов будет стремиться к бесконечности. Это приводит к глобальной бифуркации в точке
в которой рождается странный аттрактор, состоящий из бесконечного количества циклов разных порядков.

Как правило, эту диаграмму демонстрируют динамикой очень простой системы — логистистического отображения. Открытием Митчела Фейгенбаума была универсальность такого сценария и количественные характеристики последовательности бифуркаций .
Итак, мы можем подвести итог. В нашей системе можно наблюдать два основных сценария возникновения хаоса в динамических системах. Первоначальным источником хаоса на низких энергиях являются гетеро- и гомоклинические орбиты, которые соединяют седловые точки, рождаемые резонансами инвариантных торов, окружающих полюс p¹. Диффузия Арнольда постепенно расширяет границы странного аттрактора. Параллельно с этим процессом происходит ещё один — рождающиеся в резонансах полюсы сами начинают порождать последовательность резонансов с седловыми точками и полюсами более высоких порядков. Наконец, все они неизбежно превращаются в седловые точки с гомоклиническими орбитами, а потом пополняют ряды странных аттракторов через последовательность Фейгенбаума. Такая и фрактальная динамика в конце концов, превращает все точки фазового пространства в область действия глобального странного аттрактора и заполняет его глобальным хаосом.
* * *
Что-то уже много получилось. А ведь ещё ничего не сказано о количественных характеристиках странных аттракторов: экспонентах Ляпунова, фрактальной размерности, энтропии, мультиспектральности... В следующей части я расскажу и об этом.