8. Качество переходного процесса ч.1 / Хабр

8.1 Требования качества управления и основные характеристики переходного процесса.

Качество управления состоит из трех основных частей:

устойчивость;
точность;
качество переходного процесса.

Причем главным – несомненно является устойчивость систем автоматического регулирования (САР), т.к. если САР – неустойчива, то говорить о точности и тем более, о качестве переходного процесса нет смысла. Не случайно большой раздел лекций посвящен именно анализу устойчивости:

Устойчивость мы рассматривали в 4 лекциях раннее: 6 Устойчивость систем ав��оматического регулирования. Теоремы Ляпунова. Критерий устойчивости Гурвица. 6.4 Устойчивость систем автоматического регулирования. Частотный критерий устойчивости Михайлова. 6.5. Частотный критерий Найквиста. 6.6 Понятие об областях устойчивости.

Поэтому анализ САР начинают всегда с определения условий устойчивости САР (в том числе и запасов устойчивости), затем оценивается (определяется) точность САР и затем анализируется качество переходного процесса.

Точность мы рассмаривали в двух лекциях Точность систем автоматического регулирования часть 1 и часть 2

Если САР – устойчива, то при подаче управляющего воздействия система управления должна с какой-то степенью точности за какое-то время «отработать» управляющее воздействие.

Пусть САР замкнутая, тогда управляюще воздействие сутпенчатое воздействие $x(t)=a\cdot1(t)$ должно приводить выход к величине е $y\approx a$ c некоторой задержкой и возможно некторой погрешностью для $\varepsilon_{уст}$ статических САР (см. Рисунок 8.1.2).

С точки зрения практики, требуется, чтобы переход к установившемуся состоянию регулируемой величины (выходного воздействия), во-первых, проходил быстро, во-вторых, плавно, в-третьих, отклонения (колебания) регулируемой величины от заданного закона управления были минимальными.

Обычно качество переходного процесса оценивают по реакции САР на ступенчатое воздействие (в том числе и единичное). Рассмотрим некоторую САР, которая при $t\le0$ находилась в состоянии равновесия (покоя) и при подаче управляющего ступенчатого воздействия должна перейти в новое установившееся $y_{уст}$ (равновесное) состояние.

Рисунок 8.1.3 Характеристики переходного процесса

Обозначение на рисунке:

$y_{уст}\equiv y_{\infty}$ - Установившиеся значение выхода при $t\rightarrow\infty$

$y_{уст}\equiv y_{\infty}=\lim_{t\rightarrow\infty}y(t)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.1)}$

$\sigma$ - Перерегулирование превышение максимального значения выхода в переходном процессе над установившемся значением выхода.

$\sigma =\frac{y_{max}-y_{\infty}}{y_\infty}=\frac{y_{max}-y_{уст}}{y_{уст}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.2)}$

$T_{ПП}$ - время переходного процесса, т.е. то значение $t=T_{ПП}$ при котором «входит в полосу» шириной $2\cdot \Delta$ , где $\Delta$ - допуск на точность нового значения регулируемой величины.

Главными характеристиками переходного процесса принято считать:

$\sigma$ - перерегулирование;

$T_{ПП}$ - время переходного процесса;

чем меньше $\sigma$ и $T_{ПП}$ - тем обычно САР лучше.

Обычно при проектировании САР стремятся снизить величину $\sigma$ однако стремление свести $\sigma$ к нулю обычно приводит к увеличению (зачастую резкому) времени переходного процесса.

При проектировании обычно САР заранее «рисуют» «поле» переходного процесса:

Обычно, считается неплохим, если перерегулирование $\approx10 -30 \%$ , т.е. $\sigma\approx0.1\div0.3\%$ ;

В реакторных САР требования существенно более жесткие: $\sigma\approx1\div2\% \leftrightarrow 0.01\div0.02$

В некоторых САР (общетехнического назначения) считается вполне приемлимым перерегулирование и в 50÷70 %.

Время перехо��ного процесса определяется из условия:

$\frac{|y(t)-y_{\infty}|}{y_\infty}=\frac{|y(t)-y_{уст}|}{y_{уст}}\le\Delta \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.3)}$

Часто характеристикой переходного процесса является и число колебаний, т.е. количество колебаний относительно (или ). Нередко используется понятие плавность переходного процесса, т.е. ограничения по скорости и ускорению.

8.2 Интегральные оценки качества переходного процесса.

Для количественной и качественной оценки качества переходного процесса используют следующие оценки:

- интегральные;

- корневые;

- частотные;

Наиболее простой и наиболее наглядной оценкой качества переходного процесса является интегральная оценка: с помощью одного числа, вычисленного одинаковым способом для сравниваемых систем, можно сказать, какая система имеет лучшее качество переходного процесса.

Введем новую функцию, отклонение от установившегося заначения $y_1(t)=y_\infty-y(t) \equiv y_{уст}-y(t)$

Рисунок 8.2.2 Функция отклонения в разных переходных процессах

Существуют несколько типов интегральных оценок:

Простая:

$J_1=\int^{\infty}_0 y_1(t)dt=\int^{\infty}_0[y_\infty-y(t)]dt \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.2.1)}$

Данная оценка наиболее справедлива для монотонных переходных процессов чем меньше , тем САР имеет «лучший» переходный процесс, т.е. динамическая погрешность меньше и время переходного процесса меньше.

Однако для колебательных переходных процессов такая оценка не совсем корректна, т.к. в принципе, для незатухающего колебательного переходного процесса можно получить и нулевую оценку .

Рисунок 8.2.3 Возможная ошибка простой оценки

Более предпочтительно в этом случае использовать улучшенную простую оценку

$J^*_1=\int_0^\infty|y_1(t)|\cdot dt=\int_0^\infty[y_\infty-y(t)]\cdot dt\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.2.2)}$

Более часто для колебательных переходных процессов используют либо квадратичную оценку, либо улучшенную квадратичную оценку. Квадратичная оценка:

$J_2=\int^\infty_0y_1^2(t)\cdot dt=\int_0^\infty[y_\infty-y(t)]^2\cdot dt\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.2.3)}$

Улучшенная квадратичная оценка:

$J_2^*=\int_0^\infty \left\{y_1^2(t)+ [\tau\cdot y'_1(t)]^2 \right\}\cdot dt \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.2.4)}$

/- производная по времени; $y_1'(t)=\frac{dy_1(t)}{dt}$

$\tau$ - желаемое время переходного процесса.желаемое время переходного процесса.желаемое время переходного процесса.

Первое слагаемое в подынтегральной функции – учитывает величину динамической ошибки, а второе слагаемое – учитывает плавность переходного процесса. Данная оценка учитывает одновременно и быстроту переходного процесса, и его плавность.

Чем меньше - тем переходный процесс лучше.

8.3 Связь переходного процесса с частотными характеристиками замкнутой САР

Как упоминалось в п.8.2 качество переходного процесса можно оценивать с помощью частотных свойств (характеристик) замкнутой САР.

Рассмотрим некоторую линейную (или линеаризованную) САР

Рисунок 8.3.1 Типовая линеаризованную САР

Главная передаточная функция замкнутой САР: $\Phi(s)=\frac{W(s)}{1+W(s)}$

где: - передаточная функция разомкнутой САР,

причем для статических САР передаточная функция: $W(s)=\frac{K\cdot N(s)}{L_1(s)}$ ,

для астатических САР передаточная функция: $W(s)=\frac{K\cdot N(s)}{s^v\cdot L_1(s)}$

где:
- порядок астатизма; многочлены , и имеют свободные члены, равные 1 (Подробнее про статические и астатические САР см. Точность система автоматического регулирования ч.1)

Рассмотрим переходный процесс в замкнутой САР при ступенчатом входном управляющем воздействии . Если $x(t)=a\cdot1(t)$ - идея выводов принципиально не изменится.

$1(t)= \left \{ \begin{align} 1,если \ \ t>0\\0, если \ \ t\le0 \end{align} \right.$

Используя преобразования Лапласа, имеем:

$Y(s)=\Phi(s)\cdot X(s)=\frac{\Phi(s)}{S}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.3.1)}$

где: $y(t)\rightarrow Y(s); x(t)\rightarrow X(s)=\frac{1}{s}$ .

Если замкнутая САР – устойчива, то переходный процесс имеет примерно следующий вид, как на рисунке 8.3.2.

Рисунок 8.3.2 Переходной процесс устойчивой системы

Для строгости выкладок используем двухстороннее преобразование Лапласа согласно справочникам по математике:

$Z_B\left[f(t)\right]=\int_{-\infty}^\infty f(t)\cdot e^{-s\cdot t}dt \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.3.2)}$

где: $t\in]-\infty;\infty[;\ \ \ \ \ S=c+i\cdot\omega;\ \ \ \ \ \ \ \ f(t)$ - функция времени в области R (действительных числе).

Учитывая, что в рассматриваемом случае (см рисунок) , если $t\le0$ , то получим:

$Z_B\left[f(t)\right]=\int_{-\infty}^\infty f(t)\cdot e^{-s\cdot t}dt\equiv Z[f(t)]=\int_0^\infty f(t)\cdot e^{-s\cdot t}dt \ \ \ \ \ \ \ \mathbf{(8.3.3)}$

Т.е. двухстороннее преобразование Лапласа совпадает с обычным преобразованием Лапласа (односторонним).

Соотношение, аналогичное (8.3.3) можно записать и для обратных преобразований Лапласа, если при $t\le0$ .

$Z_B^{-1}[F(s)]=Z^{-1}[F(s)]+\frac{c}{2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.3.4)}$

где: - абсцисса абсолютной сходимости. Подробнее про преобразование Лапласа здесь...

Подставляя в соотношение (8.3.4) вместо выражение для получаем:

$y(t)=Z_B^{-1}[Y(s)]=Z_B^{-1}\left [\frac{\Phi(s)}{s}\right]=Z^{-1}\left[\frac{\Phi(s)}{s}\right]+\frac{c}{2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.3.5)}$

Прежде чем преобразовывать выражение (8.3.5), получим ряд соотношений и упрощающих допущений:

Во первых найдем $\lim_{t\rightarrow0}y(t):$

$\lim_{t\rightarrow0}y(t)=\lim_{s\rightarrow0}s\cdot Y(s)=\lim_{s\rightarrow 0}s\cdot\frac{\Phi(s)}{s}=\Phi(0)$ $y_{\infty}=y_{уст}=\Phi(0)=P(0)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.3.6)}$

где: - значение вещественной части АФЧХ при $\omega =0$ . Поскольку: $\Phi(i\cdot\omega)=P(\omega)+i\cdot Q(\omega)$ (см. АФЧХ САР)

Рисунок 8.3.3 Вещественная и мнимая часть АФЧХ

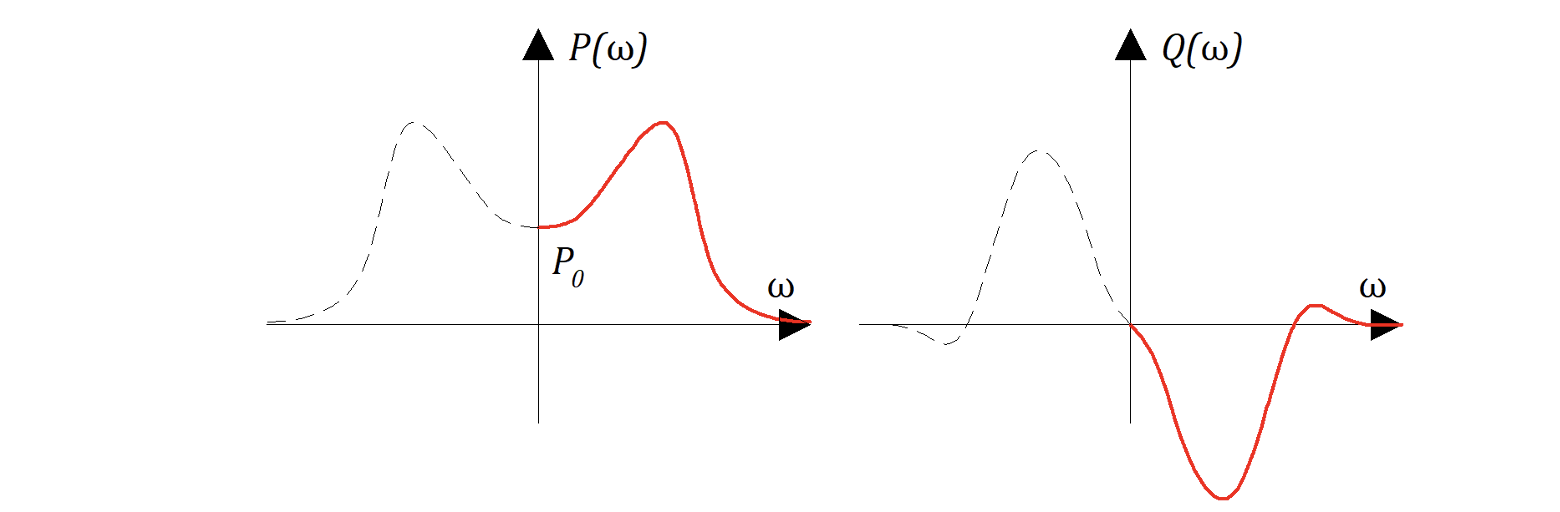
Следовательно, установившееся значение регулируемой величины числено равно - значение вещественной части АФЧХ замкнутой САР при $\omega=0$ .

Поскольку подинтегральная функция в (8.3.5) имеет нулевой полюс (), то нахождение обратного преобразования Лапласа нужно делать «осторожно», т.к. при имеет место разрыв подынтегральной функции. Сделаем некоторые преобразования:

$y(t)=Z^{-1}\left[\frac{\Phi(s)}{s}\right]+\frac{c}{2}=Z^{-1}\left[\frac{\Phi(s)-\Phi(0)}{s}\right]+Z^{-1}\left[\frac{\Phi(0)}{s}\right]+\frac{c}{2} \ \ \ \ \ \ \mathbf{(8.3.7)}$

Покажем, что нахождение составляющей (*) не представляет «опасности» при .

1 случай статическая САР:

Пусть: $W(s)=\frac{k\cdot N(s)}{L(s)}$

где: $N(s)=b_m\cdot s^m+\cdots+b_1\cdot s+1;$ $L(s)=a_n\cdot s^n+\cdots+a_1\cdot s+1$

Тогда $\lim_{s\rightarrow0}\left[\frac{\Phi(s)-\Phi(0)}s{}\right]$ - получаем неопределенность типа $\frac{0}{0}$ .

Раскроем неопределенность по правилу Лопиталя: "Предел отношения функций, стремящихся одновременно к бесконечности или к нулю (являющихся одновременно бесконечно большими или бесконечно малыми), равен пределу отношения их производных."

$\lim_{s\rightarrow0}\left[\frac{\Phi(s)-\Phi(0)}{s}\right]=\lim_{s\rightarrow0}\frac{\Phi'(s)}{1}=\Phi'(0), где \ \ \Phi'(s)=\frac{d\Phi(s)}{ds};$ $\Phi'(s)=\left [\frac{W(s)}{1+W(s)} \right]'=\left[\frac{k\cdot N(s)}{L(s)+k\cdot N(s)}\right]'$ $\Phi'(s)=k\cdot\frac{d}{ds}\left[\frac{b_m\cdot s^m+\cdots+b_1\cdot s+1}{a_n\cdot s^n+\cdots+a_1\cdot s+1+k\cdot(b_m\cdot s^m+\cdots+b_1\cdot s+1)}\right]\Rightarrow$ $\left . \frac{d\Phi(s)}{ds} \right | _ {s=0} =\Phi'(0)=k\cdot\frac{b_1\cdot(1+k)-(a_1+k\cdot b_1)}{(1+k)^2}=k\cdot\frac{b_1-a_1}{(1+k)^2}\Rightarrow$

т. е. предел существует, причем если , то $\lim_{s\rightarrow0}\Phi'(s)\rightarrow0$

2-й случай астатическая САР:

Пусть $W(s)=k\cdot\frac{N(s)}{s^\nu\cdot L_1(s)}$ , где $L_1(s)=a_{n-\nu}\cdot s^{n-\nu}+\cdots+a_1\cdot s+1$

Используя то же правило Лопиталя:

$\lim_{s\rightarrow 0}\left[\frac{\Phi(s)-\Phi(0)}{s}\right]= \lim_{s\rightarrow0}\frac{\Phi'(s)}{1}=\left. \frac{d\Phi(s)}{ds}\right|_{s=0}=$ $=\frac{d}{ds}\left[\frac{W(s)}{1+W(s)}\right]=\frac{d}{ds}\left[\frac{k\cdot N(s)}{L(s)+k\cdot N(s)}\right]=$ $=\left.k\cdot\frac{d}{ds}\left[\frac{b_m\cdot s^m+\cdots+b_1\cdot s+1}{s^{\nu}\cdot(a_{n-\nu}\cdot s^{n-\nu}+ \cdots+a_1\cdot s+1)+k\cdot(b_m\cdot s^m+\cdots+ b_1\cdot s+1)}\right]\right|_{s=0}$

Даже при $\nu=1$ , $\lim_{s\rightarrow 0}\left[\frac{\Phi(s)-\Phi(0)}{s}\right]=k\cdot\frac{b_1\cdot k-(1+k\cdot b_1)}{k^2}=-\frac{1}{k}$ - предел существует!

Поскольку подинтегральная функция в (8.3.5) не имеет особой точки (разрыва при ), то можно воспользоваться обычной формулой обратного преобразования Лапласа:

$Z^{-1}\left[\frac{\Phi(s)-P(0)}{s}\right]=\lim_{\omega\rightarrow\infty}\frac{1}{2\cdot\pi\cdot\ i}\int_{c-i\cdot\omega}^{c+i\cdot\omega}\frac{\Phi(s)-P(0)}{s}e^{s\cdot t}ds$

Т.к. можно принять, что (обычно в УТС), то:

$Z^{-1}\left[\frac{\Phi(s)-P(0)}{s}\right]=\lim_{\omega\rightarrow0}\frac{1}{2\cdot\pi\cdot i}\int_{-i\cdot \omega}^{+i\cdot\omega}\frac{\Phi(i\cdot\omega)-P(0)}{i\cdot\omega}e^{i\cdot\omega\cdot t}di\omega=$ $=\frac{1}{2\cdot \pi}\int_{-\infty}^{+\infty}\frac{\Phi(i\cdot\omega)-P(0)}{i\cdot\omega}e^{i\cdot \omega}d\omega$

Учитывая, что $e^{i\cdot \omega \cdot t}=cos(\omega\cdot t)+i\cdot sin(\omega\cdot t)$ , получаем:

$y(t)=P(0)\cdot1(t)+\frac{1}{2\pi}\int_{-\infty}^{+\infty}\frac{P(\omega)+i\cdot Q(\omega)-P(0)}{i\cdot\omega}\cdot(cos(\omega t)+i\cdot sin(\omega t))d\omega$

Раскрывая скобки получаем по 6 отдельных интегралов см. рисунок 8.3.3:

$y(t)=P(0)\cdot 1(t)+\frac{1}{2\cdot\pi}\left \{ \int_{-\infty}^\infty\frac{P(\omega)\cdot cos(\omega\cdot t)}{i\cdot\omega}d\omega+\int_{-\infty}^{\infty}\frac{P(\omega)\cdot i\cdot sin(\omega\cdot t)}{i\cdot \omega}d\omega+\\ +\int_{-\infty}^\infty\frac{i\cdot Q(\omega)\cdot cos(\omega\cdot t)}{i\cdot \omega}d\omega+\int_{-\infty}^\infty\frac{i\cdot Q(\omega)\cdot i\cdot sin(\omega\cdot t)}{i\cdot \omega}d\omega- \\-\int_{-\infty}^\infty\frac{P(0)\cdot cos(\omega\cdot t)}{i\cdot \omega} d\omega-\int_{-\infty}^\infty\frac{P(0)\cdot i\cdot sin(\omega\cdot t)}{i\cdot\omega}d\omega\right \}$

Сокращаем во всех дробях и анализируем функции на их четность и нечетность, при этом первый, четвертый и пятый интегралы равны нулю, т.к. подынтегральные функции – нечетные, а в трех оставшихся – четные см. рис. 8.3.3:

$y(t)=P(0)\cdot 1(t)+\frac{1}{2\cdot\pi}\left \{ \underbrace{\int_{-\infty}^\infty\frac{P(\omega)\cdot cos(\omega\cdot t)}{i\cdot\omega}d\omega}_0+\int_{-\infty}^{\infty}\frac{P(\omega)\cdot sin(\omega\cdot t)}{ \omega}d\omega+\\ +\int_{-\infty}^\infty\frac{ Q(\omega)\cdot cos(\omega\cdot t)}{ \omega}d\omega+\underbrace{ \int_{-\infty}^\infty\frac{i\cdot Q(\omega)\cdot sin(\omega\cdot t)}{ \omega}d\omega}_0- \\-\underbrace{\int_{-\infty}^\infty\frac{P(0)\cdot cos(\omega\cdot t)}{i\cdot \omega} d\omega}_0-\int_{-\infty}^\infty\frac{P(0)\cdot sin(\omega\cdot t)}{\omega}\right \}$

Для четных функция, можно интегрировать от 0 до $\infty$ и результат умножить на 2:

$y(t)=P(0)\cdot 1(t)+\frac{1}{\pi}\left \{ \int_{0}^{\infty}\frac{P(\omega)\cdot sin(\omega\cdot t)}{ \omega}d\omega +\int_{0}^\infty\frac{ Q(\omega)\cdot cos(\omega\cdot t)}{ \omega}d\omega- \\-P(0)\cdot\int_{0}^\infty\frac{ sin(\omega\cdot t)}{\omega}d\omega\right \}$

"Легко" видеть, что мы получили интеграл Дирихле в третьем слагаемом:

$\int_{0}^{\infty}\frac{sin(\omega\cdot t)}{\omega}d\omega=\frac{\pi}{2}$

Доказательства этого равенства в видео Интеграл Дирихле. С учетом данного интеграла получаем, а так же выражения для :

$P(0)\cdot 1(t)=\left\{ \begin{align} P(0),если \ \ t <0;\\0,если\ \ t\le 0. \end{align} \right.$

То получаем, для :

$y(t)=P(0)+\frac{1}{\pi}\int_0^{\infty}\frac{P(\omega)\cdot sin (\omega\cdot t)}{\omega}d\omega+\frac{1}{\pi}\int_0^{\infty}\frac{Q(\omega)\cdot cos(\omega\cdot t)}{\omega}d\omega -\frac{P(0)\cdot \pi}{\pi\cdot 2}$

Упрощая получаемя для

$y(t)=\frac{1}{2}P(0)+\frac{1}{\pi}\int_0^{\infty}\frac{P(\omega)\cdot sin (\omega\cdot t)}{\omega}d\omega+\frac{1}{\pi}\int_0^{\infty}\frac{Q(\omega)\cdot cos(\omega\cdot t)}{\omega}d\omega \ \ \mathbf{(8.3.9)}$

Если $t\le0$ , то $y(t)=0 \Rightarrow$

$0=\frac{1}{2}P(0)-\frac{1}{\pi}\int_0^\infty\frac{P(\omega)\cdot sin(\omega\cdot t)}{\omega}d\omega+\frac{1}{\pi}\int_0^\infty\frac{Q(\omega)\cdot cos(\omega \cdot t)}{\omega}d\omega \ \ \mathbf{(8.3.10)}$

Складываем 8.3.9 и 8.3.10 получаем выражение переходного процесса через мнимую часть АФЧХ:

$y(t)=P(0)+\frac{2}{\pi}\int_0^\infty\frac{Q(\omega)\cdot cos(\omega\cdot t)}{\omega}d\omega \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.3.11)}$

Вычитаем из 8.3.9 выражением 8.3.10 получаем выражение переходного процесса через вещественную часть АФЧХ:

$y(t)=\frac{2}{\pi}\int_0^\infty\frac{P(\omega)\cdot sin(\omega\cdot t)}{\omega}d\omega \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.3.12)}$

Формула (8.3.12) является более предпочтительной (более удобной) и поэтому в практике используют, в основном, выражение для через вещественную часть АФЧХ замкнутой САР.

Необходимо заметить, что формула (8.3.12) описывает переходный процесс при , т.е. $y(t)\equiv h_x(t)$ , где - переходная функция замкнутой САР.

Если на вход САР подано воздействие $\delta(t)$ то выражение переходного процесса:

$y_{\delta(t)}\equiv w_x(t)=\frac{d}{dt}h_x(t)=\frac{d}{dt}\left [ \frac{2}{\pi}\int_0^\infty\frac{P(\omega)\cdot sin (\omega\cdot t)}{\omega}d\omega \right]\Rightarrow$

весовая функция замкнутой САР:

$\omega_x(t)=\frac{2}{\pi}\int_0^\infty P(\omega)cos(\omega\cdot t)d\omega \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.3.13)}$

Если на вход системы подано ступенчатое воздействие $x(t)=a\cdot1(t)$ , то:

$y(t)=\frac{2\cdot a}{\pi}\int_0^\infty\frac{P(\omega)\cdot sin(\omega\cdot t)}{\omega}d\omega\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.3.14)}$

При расчете по формуле (8.3.12) необходимо учитывать ряд особенностей:

Рисунок 8.3.4 Зависимость вещественной части от частоты

где: н.ч. – область низких частот; ср.ч. – область средних частот; выс.ч. – область высоких частот.

Область высоких частот (выс.ч.) «отвечает» (определяет) вид переходного процесса при очень малых t.

Область низких частот (н.ч.) – определяет переходный процесс при очень больших t ( $\rightarrow\infty$ ).

Область средних частот (ср.ч.) – определяет основную часть переходного процесса (например перерегулирование).

Рисунок 8.3.5. Переходный процесс по частотны областях

вычисление по формуле (8.3.12) с использованием численных алгоритмов (например метода трапеций и т.д.) приводит к следующим преобразованим:

$y(t_*)=\frac{2}{\pi}\left \{ P_1\int_0^{\omega_1}\frac{sin(\omega\cdot t_*)}{\omega}d\omega+P_2\int_{\omega_1}^{\omega_2}\frac{sin(\omega\cdot t_*)}{\omega}d\omega+..\\..+P_j\int_{\omega_{j-1}}^{\omega_j}\frac{sin(\omega\cdot t_*)}{\omega}d\omega\right \}$

Можно заменить домножить числитель изнаметатель на и перейти к интегралу по $\omega\cdot t_*$ :

$\int_0^{\omega_1}\frac{sin(\omega\cdot t_*)}{\omega}d\omega=\int_0^{\omega_1\cdot t_*}\frac{sin(\omega\cdot t_*)}{\omega\cdot t_*}d(\omega\cdot t_*)\equiv\int_0^{Z_1}\frac{sin(Z)}{Z}dZ=Si(Z_1)$

Где:

$Z =\omega\cdot t$ - новая переменная;

- интегральный синус.

Для функции интегральный синус существуют таблицы (см. справочники по математике). Как правило в этих таблицах аргумент только до $\approx 20$ . Если , то необходимо проанализировать и скорее всего пренебречь этим слагаемым. Поскольку наша задача определить качество переходного процесса, малые отклонения при завершении нас не сильно интересуют. Вид функции представлен на следующем рисунке:

Рисунок 8.3.6 Вид функции интегрального синуса

При использовании интегрального синуса, для оценки качества переходного процесса путем численного интегрирования достаточно использовать частоты до средних и отбрасывать более высокие частоты.

Рисунок 8.3.7 Функция значение вещественной части АФЧХ разделенная по частотам

8.4 Определение величины перерегулирования при ступенчатом виде .

Рассмотрим предельный случай, года вещественная часть АФЧХ Определить перерегулирование САР, при единичном ступенчатом воздействии если замкнутая и устойчивая САР, имеет вещественную часть АФЧХ - $P(\omega)$ - представленную на рисунке:

$P(\omega)=\left\{ \begin{align} P_0, если \ \ \omega\le\omega_*;\\0,если \ \ \omega>\omega_*. \end {align} \right.$

Используя формулу 8.3.14, выражающую переходную функцию замкнутой САР через $P(\omega)$ для ступенчатого воздействия:

$y(t)\equiv h_x(t)=\frac{2}{\pi}\int_0^\infty\frac{P(w)}{w}sin(\omega\cdot t)d\omega=\frac{2\cdot P_0}{\pi}\int_0^{\omega_*}\frac{sin(\omega\cdot t)}{\omega}dt$

Введем новую переменную $Z=\omega\cdot t$ тогда $d\omega =\frac{1}{t}dZ\Rightarrow$

$y(t)=\frac{2\cdot P_0}{\pi}\int_0^{\omega_*\cdot t}\frac{sin(\omega\cdot t)}{\omega\cdot t}d\omega=\frac{2\cdot P_0}{\pi}\int_0^{Z_*}\frac{sin(Z)}{Z}dZ=\frac{2\cdot P_0}{\pi}Si(Z_*)$

- интегральный синус (см. справочники по математике).