petuhoff 4 июл 2022 в 00:37

5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР)

7 мин

27K

Анализ и проектирование систем*Алгоритмы*Математика*Промышленное программирование*Matlab*

Туториал

Продолжаем публикацию лекций по курсу "Управление в Технических Системах" автор - Олег Степанович Козлов на кафедре Э7 МГТУ им. Н.Э. Баумана.

Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется. В предыдущих сериях:

1. Введение в теорию автоматического управления.
2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ.
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности. 4 Структурные преобразования систем автоматического регулирования.

Будет как всегда позновательной увлекательно и жестко

5.1. Главная передаточная функция. Передаточные функции по возмущающему воздействию и для ошибки (рассогласования)

Используя структурные преобразования (см. раздел 4), структурную схему практически любой линейной или линеаризованной САР (САУ) можно привести к виду:

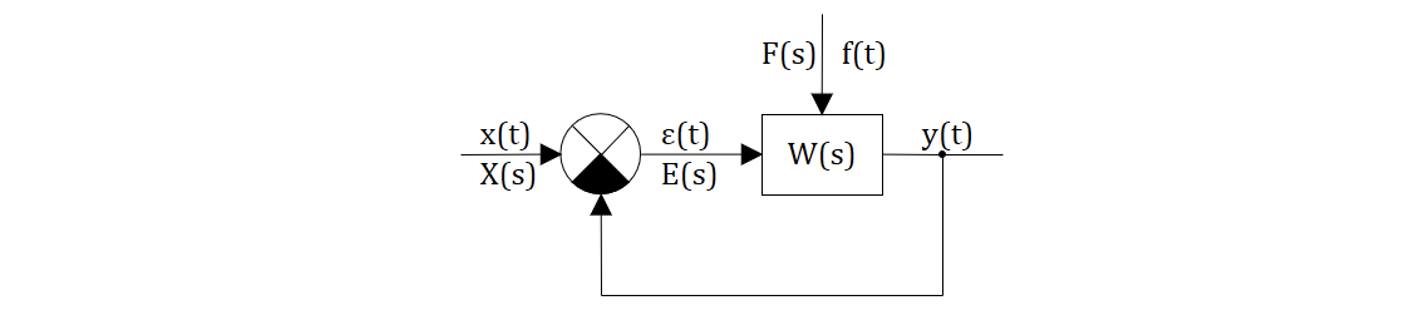
Где функции по времени:

- управляющее воздействие;

– регулируемая величина (выходное воздействие);

– возмущающее воздействие;

Или в изображениях:

$\left \{ \begin{align}x(t)&\rightarrow X(s)\\y(t)&\rightarrow Y(s)\\ f(t)& \rightarrow F(s) \\ \epsilon(t)&\rightarrow E(s) \end{align} \right.$

Определение: Если единичная обратная связь охватывает все элементы (звенья) САР – она называется главной.

Определение: Если главная обратная связь отсутствует - САР считается разомкнутой.

Передаточная функция может быть любой сложности (т.е. содержать местные обратные связи, параллельные и последовательные цепи и т.д.).

Возмущающих воздействий может быть несколько и приложены они могут быть в любом месте структурной схемы.

Передаточную функцию которую в Теории Управления называют передаточной функцией разомкнутой САР, будем представлять в следующем виде (для единообразия):

$W(s)=\frac{K\cdot N(s)}{L(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.1)}$

где – общий коэффициент усиления; – полиномы по степеням переменной , причем свободные члены в них равны 1 (единице).

Учитывая, что САР линейна или линеаризована, разделим на структурной схеме каналы прохождения управляющего и возмущающего воздействий. Выделим в отдельное звено (может быть и очень сложное) ту часть системы, через которую проходит возмущающее воздействие $f(t)\Rightarrow$ обозначим ее через $M(s)\Rightarrow$ Структурная схема САР принимает вид:

Рисунок 5.1.2 Структурная схема общего вида с передаточной функцией и внешним воздействием

где: $y_1(t)\rightarrow Y_1(s); \ \ y_2(t)\rightarrow Y_2(s); \ \ y(t)=y_1(t)+y_2(t); \ \ Y(s)=Y_1(s)+Y_2(s).$

В Теории Управления используют 3 основных передаточных функций замкнутой САР:

главная передаточная функция $\Phi(s)$ ;
передаточная функция по возмущающему воздействию $\Phi_f(s)$ ;
передаточная функция для ошибки (рассогласования) $\Phi_\varepsilon(s).$

Рассмотрим более подробно вышеупомянутые передаточные функции.

Главная передаточная функция

Главная передаточная функция -передаточная функция по управляющему воздействию математическое определение этой передаточной функции:

$\Phi(s) =\frac{Y(s)}{X(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2)}$

выведем формулу при условии если возмущеющие воздействие равно $f(t)=0, \Rightarrow y(t)=y_1(t)$ . "Обойдем" структурную схемв по контуру:

$Y(s)= E(s)\cdot W(s)=\left[ X(s)-Y(s)\right]\cdot W(s)\Rightarrow\\Y(s)=X(s)\cdot W(s)-Y(s)\cdot W (s) \Rightarrow\\Y(s)+Y(s)\cdot W(s)=X(s)\cdot W(s)\Rightarrow\\ \frac{Y(s)}{X(s)}=\frac{W(s)}{1+W(s)};$ $\Phi(s)=\frac{W(s)}{1+W(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3)}$

Примечание. Формула (5.3) совпадает с формулой для передаточной функции цепи с местной единичной обратной связью (см. раздел 4 – «Структурные преобразования»).

Подставляя вместо ее выражение через полиномы и $L(s) \Rightarrow$

$\Phi(s)=\frac{K\cdot N(s)/L(s)}{1+K\cdot N(s)/L(s)}=\frac{K\cdot N(s)}{L(s)+K\cdot N(s)}=\frac{K\cdot N(s)}{D(s)}\ \ \ \ \ \ \mathbf{(5.4)}$

где: $D(s)=L(s)+K\cdot N(s)$

Анализ выражения (5.4) показывает, что свойства главной передаточной функции замкнутой САР однозначно определяются свойствами разомкнутой САР, т.е. через полиномы и .

Передаточная функция замкнутой САР по внешнему возмущающему воздействию

Дадим математическое определение рассматриваемой передаточной функции если управляющие воздействи , а возмущеющие воздействие отличное от нуля $f(x)\neq 0$ . В этом случае (см. рисунок 5.1.2) получается:

$y(t)=y_1(t)+y_2(t)\\ x(t)=0\Rightarrow \varepsilon(t)=0-y(t)=-y(t);$

Перрейдем к изображением и "обойдем" схему (см. рис. 5.1.2) по контуру

$Y(s)=Y_1(s)+Y_2(s) =E(s)\cdot W(s)+F(s)\cdot M(s)=\\=-Y(s)\cdot W(s)+F(s)\cdot M(s) \Rightarrow\\Y(s)\cdot[1+W(s)]=F(s)\cdot M(s)\Rightarrow \frac{Y(s)}{F(s)}=\frac{M(s)}{1+W(s)};$ $\Phi_f=\frac{Y(s)}{F(s)} =\frac{M(s)}{1+W(s)}$

Подставляя вместо ее выражение через полиномы и получаем:

$\Phi_f=\frac{M(s)}{1+K\cdot N(s)/L(s)}=\frac{M(s)\cdot L(s)}{L(s)+K(s)\cdot N(s)}=\frac{R(s)}{D(s)}\ \ \ \ \ \ \ \ \mathbf{(5.6)}$

где: $R(s) =M(s)\cdot L(s)$ - вид данного полинома зависит от места приложения возмущающего воздействия;

Формулы 5.4 и 5.6 имеют общий занаменатель $D(s)=L(s)+K\cdot N(s)$

Передаточная функция замкнутой САР для ошибки (рассогласования)

Дадим математическое определение рассматриваемой передаточной функции если управляющие воздействиt отлично от 0 $x(t) \neq0$ , а возмущеющие воздействие равно 0 . В этом случае для передаточной функции получается (см. рис. 5.1.2):

$\Phi_\varepsilon(s)=\frac{E(s)}{X(s)}$

Сделаем вывод соответствующих формул, выполнив «обход» по контуру схемы (см. рис. 5.1.2) $\Rightarrow$

$E(s)=X(s)-Y(s)=X(s)-E(s)\cdot W(s)\Rightarrow \\ E(s)\cdot(1+W(s))=X(s) \Rightarrow \frac{E(s)}{X(s)}=\frac{1}{1+W(s)}$ $\Phi_\varepsilon(s)=\frac{1}{1+W(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.7)}$

Учитывая формулу для главной передаточной функции $\Phi(s)=\frac{W(s)}{1+W(s)}$ можно записать выражения для передаточной функции рассоглаосвания:

$\Phi_\varepsilon(s)=1-\Phi(s)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.8)}$

Подставляя вместо ее выражение через полиномы и получаем:

$\Phi_\varepsilon(s)=\frac{1}{1+K\cdot N(s)/L(s)}=\frac{L(s)}{L(s)+K\cdot N(s)}=\frac{L(s)}{D(s)}\ \ \ \ \ \mathbf{(5.9)}$

где: $D(s)=L(s)+K\cdot N(s)$

Опять замечаем, что знаменатель передаточной функции $\Phi_\varepsilon$ равен полиному следовательно, характерным признаком передаточных функций замкнутой САР является общность знаменателей ! ! !

В Теории Управления выражение $D(s)=L(s)+K\cdot N(s)$ имеет «собственное» название: характеристический полином замкнутой САР.

5.2 Уравнения динамики замкнутой САР

Как указывалось в подразделе 5.1, любую замкнутую САР можно привести к виду представленному на рисунке 5.2.1:

Рисунок 5.2.1 Общая схема замкнутой САР с возмущающим воздействием

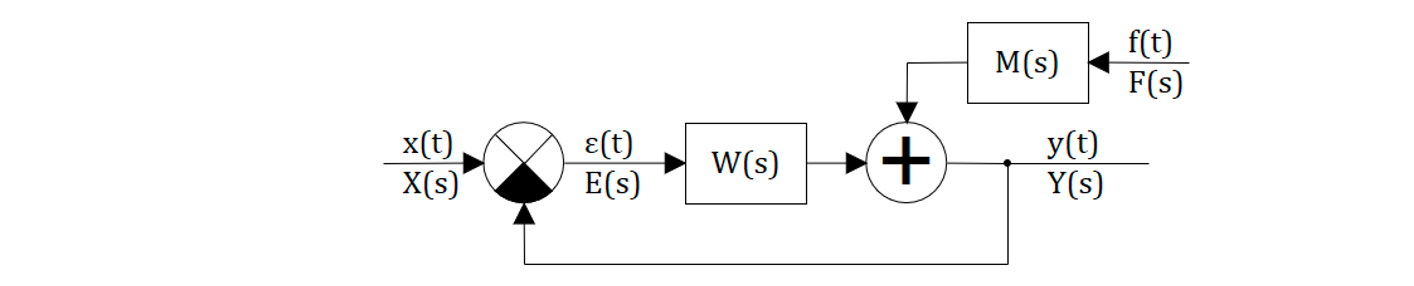
Выведены соотношения для 3-х основных передаточных функций замкнутой САР позволяют записать выражения для регулируемой величины в изображениях:

$Y(s)=\underbrace{\Phi(s)\cdot X(s)}_{Y_x(s)}+\underbrace{\Phi_f(s)\cdot F(s)}_{Y_f(s)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2.1)}$

Подставляя значения $\Phi_s(s)$ и $\Phi_f(s)$ через полиномы и разомкнутой САР получаем:

$Y(s)=\frac{K\cdot N(s)}{L(s)+K\cdot N(s)}\cdot X(s)+\frac{R(s)}{L(s)+K\cdot N(s)}\cdot F(s)$

подставим значения для характеристического полинома $D(s)=L(s)+K\cdot N(s)$ получим выражение для динамического уравнения замкнутой САР в изображениях:

$D(s)\cdot Y(s)=K\cdot N(s)\cdot X(s)+R(s)\cdot F(s)\ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2.2)}$

Переходя к оригиналам получаем символическую форму записи обыкновенного дифференциального уравнения замкнутой САР:

$D(p)\cdot y(t)=K\cdot N(p) x(t)+R(p)f(t) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2.3)}$

Решение диференциального уравнения состоит из двух частей:

$y(t)= y_{соб.}(t)+y_{вын.}(t)$

где: $y_{соб.}(t)$ - собственная часть, решение однородного дифференциального уравнения ;

$y_{вын.}$ - вынужденная часть решения (частное решение), определяемая правой частью уравнения ( 5.2.3 ).

Решения однородного уравнения замкнутой САР:

$D(p)y(t)=0 \Rightarrow a_n\cdot y^{(n)}+a_{n-1}\cdot y^{n-1}+...+a_1\cdot y^1+a_0\cdot y=0$

записываем соответствующее характеристическое уравнение:

$D(\lambda)=0 \Rightarrow a_n\cdot\lambda^n+a_{n-1}\cdot \lambda^{n-1}+...+a_1\cdot \lambda+a_0=0 \Rightarrow$

находим корни степенного уравнения $\lambda_j$ если все корни уравнения разные:

$Y_{соб}(t)=\sum_{j=1}^nC_j\cdot e^{\lambda\cdot j},$

Если есть совпадающие корни характеристического уравнения, то формула для $Y_{соб}(t)$ изменится (см. Математическое описание систем автоматического управления).

Обычно $y_{вын.}$ находят по виду правой части уравнения (5.2.3) или, используя другие методы (например, метод вариаций постоянных).

Необходимо отметить, что порядок дифференциального уравнения (5.2.3) равен «n», т.е. такой же, как и у разомкнутой САР $\Rightarrow$

$L(p)y(t)=K\cdot N(p)x(t)$

если нет возмущающего воздействия, т.к. порядок дифференциального оператора L(p) обычно значительно выше, чем N(p).

По аналогии с выводом уравнения (5.2.3) можно получить уравнение динамики для рассогласования $\varepsilon(t)$ :

$E(s)=\Phi_\varepsilon(s)\cdot X(s)-\Phi_f(s)\cdot F(s) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2.4)}$

подставляя значения $\Phi_\varepsilon$ и $\Phi_f$ (см. 5.6 и 5.9) получаем:

$E(s)=\frac{L(s)}{D(s)}\cdot X(s)-\frac{R(s)}{D(s)}\cdot F(s) \Rightarrow$ $D(s)\cdot E(s)=L(s)\cdot X(s)-R(s)\cdot F(s)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2.5)}$

Уравнение (5.2.5)- уравнение динамики замкнутой САР в ихображениях для рассогласования (ошибки) при наличии управляющего и возмущающего воздействий.

Особенностью данного уравнения (5.2.5) является то, что левая часть его практически совпадает с левой частью (5.2.2), в то время, как порядок правой части заметно выше , т.к. порядок многочленов D (s) и L (s) - одинаков, а порядок N(s) меньше L(s).

Это означает, что внешние воздействия и влияют на $\varepsilon(t)$ более сильным образом.

Дифференциальное уравнение замкнутой САР для ошибки:

$D(p)\varepsilon(t)=L(p)x(t)-R(p)f(t)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2.6)}$

Способы решения уравнения ( 5.2.6 ) такие же, как и для уравнения ( 5.2.3 ) .

5.3. Частотные характеристики замкнутой САР.

Наибольший интерес при анализе замкнутых САР имеет АФЧХ замкнутой САР по управляющему воздействию:

$\Phi(s)_{s=i\cdot\omega}=\Phi(i\cdot\omega)=\frac{W(i\cdot\omega)}{1+W(i\cdot \omega)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3.1)}$

где передаточная функция:

$W(i\cdot\omega)=\frac{K\cdot N(i\cdot\omega)}{L(i\cdot \omega)}$

Учитывая, что $W(i\cdot\omega)=u(\omega)+i\cdot v(\omega)$ - комплексное число, по аналогии имеем:

$\Phi(i\cdot\omega)=P(\omega)+ i\cdot Q(\omega) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3.2)}$

Где $P(\omega)=Re(\Phi_s)$ - вещественная часть функции, $Q(\omega)=Im(\Phi_s)$ - мнимая часть функиции.

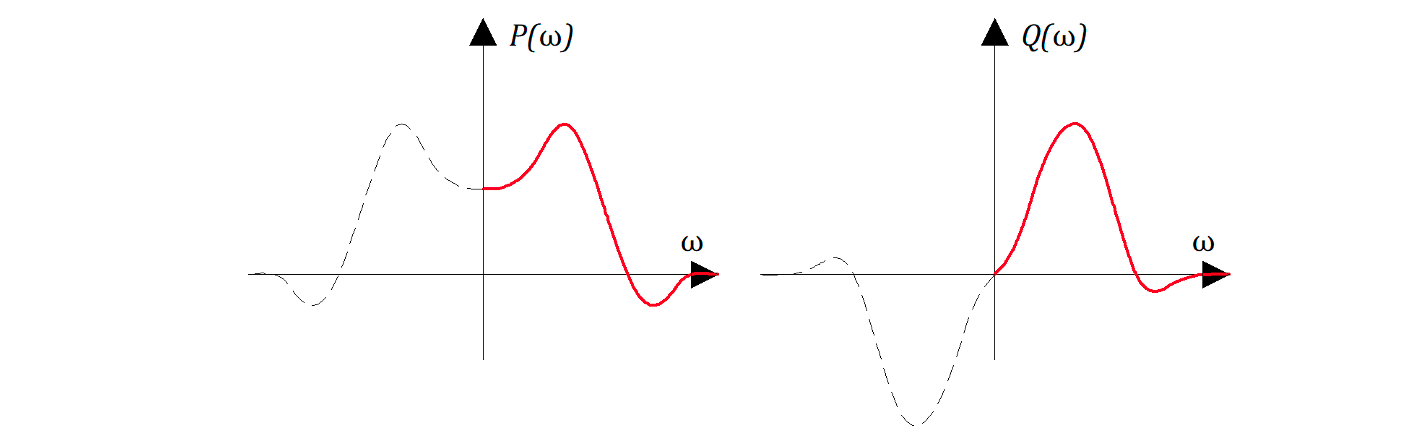
На этих рисунках представлен «примерный» вид зависимостей P (w)и Q(w) для «какой-то» замкнутой САР причем P(w) - четная функция, т.е. P(w) = P(-w); Q(w) - нечетная функция, т.е. Q(w) = - Q(-w).

Если известны частотные свойства разомкнутой САР, то можно определить частотные свойства замкнутой САР. Воспользуемся показательной формой для АФЧХ

$W(i\cdot\omega) = A(\omega)\cdot e^{i\cdot \varphi(\omega)}$

Где $A(\omega)$ - амплитуда (модуль), $\varphi(\omega)$ - сдвиг фазы (фаза). Подставляя это в (5.3.1), имеем получаем:

$\Phi(i\cdot\omega) = A_{з}(\omega)\cdot e^{i\cdot\varphi_з(\omega)}=\frac{A(\omega)\cdot e^{i\cdot \varphi(\omega)}}{1+A(\omega)\cdot e^{i\cdot \varphi(\omega)}}\Rightarrow$ $\Rightarrow 1+A(\omega)\cdot e^{i\cdot\varphi(\omega)}=\frac{A(\omega)\cdot e^{i\cdot \varphi(\omega)}}{A_{з}\cdot e^{i\cdot \varphi_з(\omega)}}\Rightarrow$ $\Rightarrow \frac{e^{-i\cdot \varphi_3(\omega)}}{A_з(\omega)}=1+\frac{e^{-i\cdot \varphi(\omega)}}{A(\omega)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3.3)}$

Учитывая, что $e^{-i\cdot \varphi}=cos(\varphi)-i\cdot sin(\varphi) \Rightarrow$

$\frac{cos[\varphi_з(\omega)]}{A_з(\omega)}-i\cdot\frac{sin[\varphi_З(\omega)]}{A_з(\omega)}=1+\frac{cos[\varphi(\omega)]}{A(\omega)}-i\cdot\frac{sin[\varphi(\omega)]}{A(\omega)}\ \ \ \ \ \ \ \mathbf{(5.3.4)}$

Приравнивая чисто вещественные и чисто мнимые части, имеем $\Rightarrow$

$\left \{ \begin {align}\frac{cos[\varphi_з(\omega)]}{A_з(\omega)}&=1+\frac{cos[\varphi(\omega)]}{A(\omega)} \ \ \ \ \ (1)\\ \frac{sin[\varphi_з(\omega)]}{A_з(\omega)}&=\frac{sin[\varphi(\omega)]}{A(\omega)} \ \ \ \ \ \ \ \ \ \ \ \ (2). \end{align} \right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3.5)}$

Для нахождения амплитуды $A_з(\omega)$ и сдвига фазы $\varphi_з(\omega)$ замкнутой передаточной функции как функции от амплитуды $A(\omega)$ и сдвига фазы $\varphi (\omega)$ разомкнутой системы. Разделив (2) на (1) получим:

$tg[\varphi_з(\omega)]=\frac{sin[\varphi(\omega)]}{A(\omega)+cos[\varphi(\omega)]} \Rightarrow$

Сдвиг фазы замкнутой системы через характеристики разомкнутой системы:

$\varphi_з(\omega) = arctg \left[ \frac{sin[\varphi(\omega)]}{A(\omega)+cos[\varphi(\omega)]}\right] - \pi\cdot j \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3.6)}$

Для получения амплитуды замкнутоей системы возведем оба уравнения системы (5.3.5) в квадрат: $\Rightarrow$

$\left \{ \begin {align}\frac{cos^2[\varphi_з(\omega)]}{A^2_з(\omega)}&=1+\frac{cos^2[\varphi(\omega)]}{A^2(\omega)}+2 \cdot\frac{cos[\varphi(\omega)]}{A(\omega)} ;\\ \frac{sin^2[\varphi_з(\omega)]}{A_з^2(\omega)}&=\frac{sin^2[\varphi(\omega)]}{A^2(\omega)} . \end{align} \right.$

складываем эти два уравнения:

$\frac{1}{A^2_з(\omega)}\left[\underbrace{cos^2\varphi_з(\omega)+sin^2\varphi_з(\omega)}_1\right]=1+\frac{1}{A^2(\omega)}\left[\underbrace{cos^2\varphi(\omega)+sin^2\varphi(\omega)}_1\right]+\dots\\\dots+2\frac{cos[\varphi(\omega]}{A(\omega)}$ $\frac{1}{A^2_з(\omega)}=\frac{A^2(\omega)+2\cdot A\cdot cos[\varphi(\omega)]+1}{A^2(\omega)}\Rightarrow$ $A_з(\omega)=\frac{A(\omega)}{\sqrt{A^2(\omega)+2\cdot A(\omega)\cdot cos[\varphi(\omega)]+1}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3.7)}$

Аналогичным образом можно выразить, например, P(w) и Q(w) - характеристики замкнутой САР через u(w) и u(w) - характеристики разомкнутой САР.

Пример

В качестве примера на рисунке 5.4.1 приведена модель помещения, в котором с помощью интегрирующего звена обеспечивается подвод тепла для поддержания температуры. Температура задается в виде ступенчатой функции. В качестве внешнего воздействия используется внешняя температура.

5.4.1 Рисунок сравнение физической модели и передаточных функций

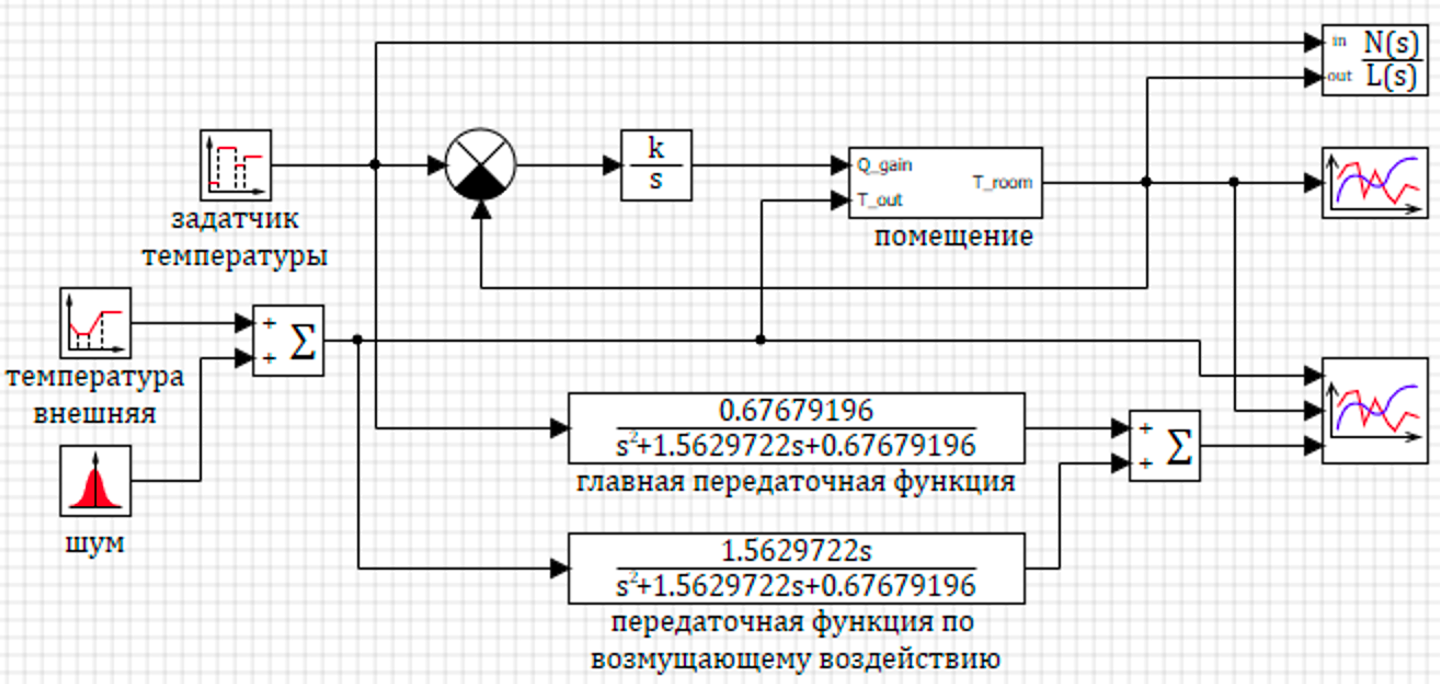
Передаточные функции построены средтвами автоматического анализа. Видно, что знаменатель главной передаточной функции и знаменатель передаточной функции по возмущающиму воздействию одинаковы.

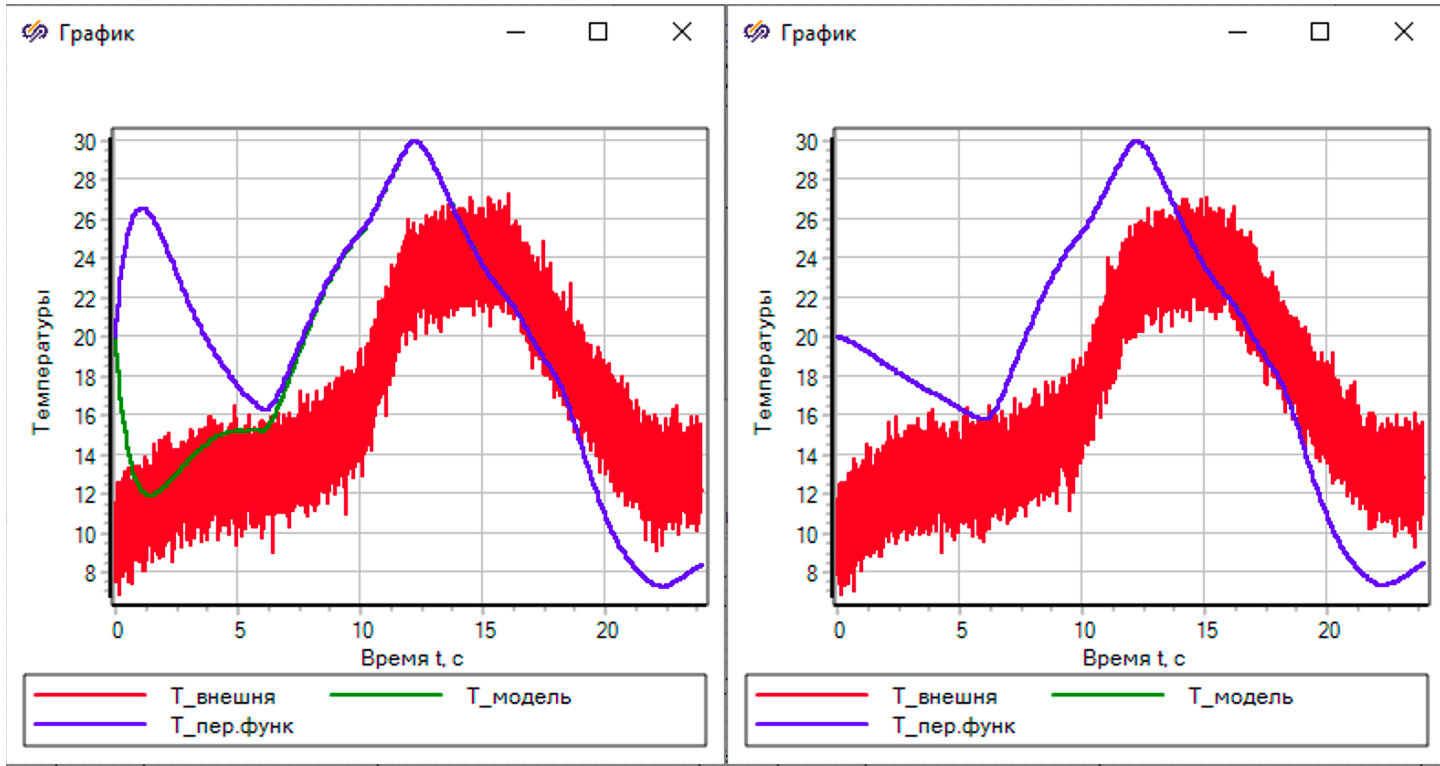
График справа показывает расхождение результаты модели (зеленая линия) и передаточных функций (синит линя) в начале расчета, но потом функции сходятся. Расхождение объясняются разными начальными условиями по производным. Слева тот же самый график, но в это случае начальное состояние определено с помощю загрузки стационарного состояния, полученного предварительным моделированием. В этом случае совпадение модели и передаточных функций полное.

Ссылку на модель примера можено взять здесь...

Теги:

Хабы:

Если эта публикация вас вдохновила и вы хотите поддержать автора — не стесняйтесь нажать на кнопку

5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР)

5.1. Главная передаточная функция. Передаточные функции по возмущающему воздействию и для ошибки (рассогласования)

Главная передаточная функция

Передаточная функция замкнутой САР по внешнему возмущающему воздействию

Передаточная функция замкнутой САР для ошибки (рассогласования)

5.2 Уравнения динамики замкнутой САР

5.3. Частотные характеристики замкнутой САР.

Пример

Публикации

Истории

Работа

Ближайшие события